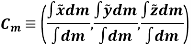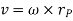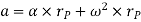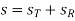UNIT 5
Properties of areas
Theory of relativity explains that the velocity or acceleration of a particle varies with the change in the frame of reference.
Consider an example, a train is moving. For the observer who is standing on a station, the train is moving with some velocity and acceleration. But for the person sitting inside the train, the train is stationary. For the person in a car travelling in the same direction of the train parallel to the train track, the train is moving with some velocity and acceleration, but the magnitude of velocity and acceleration are different than the magnitude of velocity and acceleration with respect to the person standing on a station.
Consider, two frame of references S and S’ in a relative motion with each other. Let 
be the position vector of the origin of the frame of reference S’ from the origin of original frame of reference S as shown in figure below.
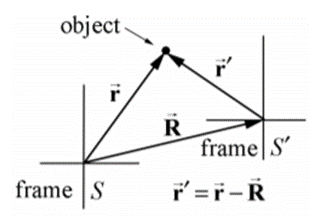
Consider on object or a particle in motion, whose position is defined by 
from the origin of frame of reference S and 
w.r.t the frame of reference S’.
Then the position vectors are related by the law of vector addition.
The relative velocity of the two frames of references is given by the time derivative of the position vector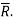 
If the relative velocity between the two frames of reference is constant then the relative acceleration is zero.
If the relative velocity varies, then the acceleration is given by the time derivative of the relative velocity vector.
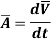
The velocity of the particle w.r.t the original frame of reference S and frame of reference S’ is also the time derivative of the respective position vectors.
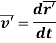
The acceleration of the particle w.r.t the original frame of reference S and frame of reference S’ is also the time derivative of the respective velocity vectors.
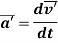
Now, we have,
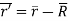
Taking time derivative of the above equation, we get
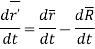
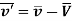
This is called as the law of addition of velocities
Now taking time derivative of the above equation, we get,
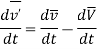
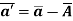
This law is called as the law of addition of acceleration.
Center of mass is the point on an object, where the weight of the body acts.
Consider a body of total mass m and having center of mass as Cm.
A body is composed of an infinite number of particles of differential size. Consider one particle of mass 
, weight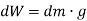 
and location (
) as shown in figure
Weights of each particle will form an approximately parallel force system, and the resultant of this system is the total weight of the body W, which passes through a single point called the center of gravity G.
i.e. the weight of the body is the sum of the weights of all of its particles
Also, mass of body is the sum of the mass of each particle of the body
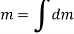
Now, the moment of W about x-axis is equal to the sum of moment of weights of each particles about same axis.
We get,
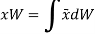
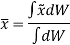
Now, as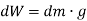 
and 
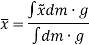
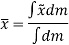
Similarly, if moments are summed about the y axis,
We get,
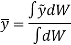
Now, consider that the body is fixed within the coordinate system and this system is rotated about the y axis as shown in fig
In similar manner, if moments are summed about the z axis, we get,
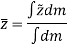
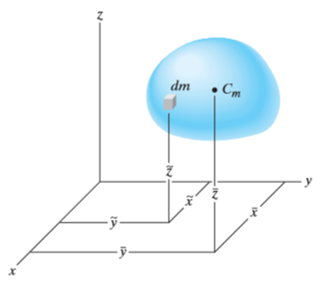
Hence, the location of center of mass with respect to x, y, z axes is
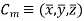
Moments of Inertia for Areas:
When a distributed loading whose intensity varies linearly acts perpendicular to an area, the computation of the moment of the loading distribution about an axis involves a quantity called the moment of inertia of the area or simply area moment of inertia.
Consider a differential plate, subjected to fluid pressure P that varies linearly with depth, as shown in fig, such that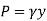 
, where, 
is the specific weight of fluid.
The force acting on an acting on the differential area of the plate is given by
The moment of this this force about the x-axis is
Integrating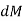 
over the entire area of the plate yields
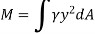
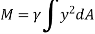
The integral part of the moment equation is called area moment of inertia about x-axis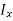 
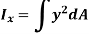
Similarly, area moment of inertia about y-axis is given as,
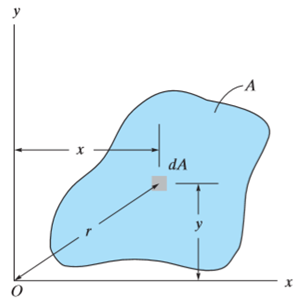
Moment of Inertia for area can also be given as
Where, A is the total area
And k is referred as radius of gyration
Radius of gyration for area of a plate about an axis is defined as the radial distance to a point which would have a same moment of inertia as the plate’s actual distribution of area, if the total area of the plate were concentrated.
It is given by,
Parallel axis theorem for Area
It states that “the moment of Inertia about an axis is equal to the summation of moment of inertia about the axis passing from centroid of area and the product of total area and square of perpendicular distance between the two axes.”
Mathematically,
Where,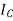 
is the moment of inertia about axis passing through the centroid, and d is the perpendicular distance between two axes.
For the system shown below,
Mass moment of Inertia:
The mass moment of inertia of a body is a measure of the body’s resistance to angular acceleration.
Consider a rigid body, rotating about z-axis, as shown in figure.
Mass moment of inertia is defined by,
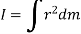
Where, r is the perpendicular distance from the axis of rotation to the arbitrary differential element of the body of mass dm.
The moment of inertia is also written as
Where, m is the total mass of the body
And k is referred as radius of gyration
Radius of gyration for a body rotating about an axis is defined as the radial distance to a point which would have a same moment of inertia as the body’s actual distribution of mass, if the total mass of the plate were concentrated.
In simple words, radius of gyration is the perpendicular distance of the axis of rotation to the point where the entire mass of the body is supposed to be concentrated for dynamic analysis.
It is given by,
Theorem of parallel axes for mass
Theorem of parallel axes states that, “the moment of inertia of the rotating body about an axis is equal to the summation of the moment of inertia of the body about an axis passing through the center of mass and the product of total mass of the body and the square of perpendicular distance between the two axes.”
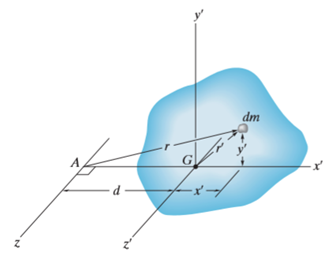
Mathematically,
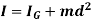
Where,
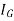= Moment of inertia about z’ axis passing through the center of mass G
m = total mass of body
d = perpendicular distance between the parallel axes
Theorem of perpendicular axes
It states that, “for the planar element, the moment of inertia about an axis is equal to the summation of moment of inertias about two mutually perpendicular axes.”
Mathematically,
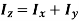
A rigid body is an ideal body that does not change its shape when subjected to external forces or couples. The distance between the particles in a rigid body remains same during the motion. Hence, a rigid body can be defined as the group or collection of number of particles at fixed distance from each other.
There are three types of motion of a rigid body
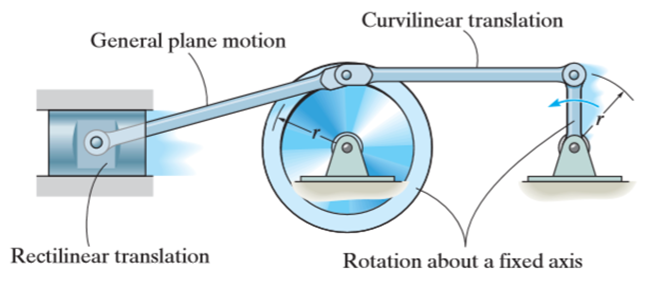
Kinematics of rigid body in translation motion
Translation motion occurs when a line (generally axis) in the body remains parallel to its initial orientation throughout the motion.
If the path of motion of any two lines on the rigid body are parallel or are in a straight line, then the translation is termed as rectilinear translation.
If the path of motion of any two lines on the rigid body are along the fixed curve, then the translation is termed as curvilinear translation.
Consider a rigid body that is subjected to translation motion as shown in fig.
The position of points A and B is defined are defined by the position vectors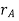 
and 
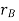w.r.t the fixed frame x, y.
Let the translating system is fixed in a body with origin A which is referred to the base point. The position vector of B w.r.t A is denoted by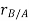 
.
By vector addition, we get,
Taking, the first time derivative of the above equation, we get,
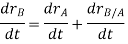
According to the definition of rigid body, the term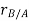 
is constant
Hence,
And,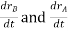 
gives the absolute velocities 
and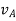 
respectively with respect to the fixed frame.
So, we get,
This shows that, for the rigid body in translation motion, the velocity of every particle on the body is same.
Now, taking the time derivative of the velocity equation, it simply yields
Where,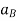 
and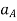 
are the absolute accelerations of points A and B on the rigid body w.r.t fixed frame.
This shows that, for the rigid body in translation motion, the velocity and acceleration of every particle on the body is same.
Kinematics of a body rotating about fixed axis
When a rigid body is subjected to the rotation about a fixed axis, as shown in fig below, all the particles of the body, except those which lie on the axis of rotation, move along circular paths whose center lies on the axis of rotation.
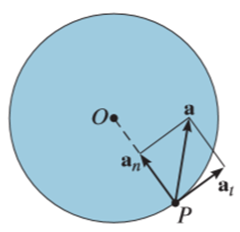
Consider, the point P on the rigid body defined by the position vector r. As the rigid body rotates about the fixed axis, then the point P travels a circular path of radius r with center point O as shown in fig below
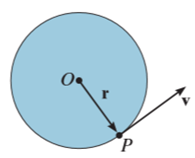
If the body rotates with a differential angular displacement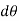 
, then the point P displaces the distance 
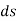, which is given by
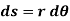
Differentiating the above equation w.r.t time, we get
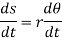
The term, 
is referred to as the angular velocity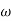 
of the rotating body
And 
gives the velocity of point P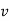 
Hence,
The direction of velocity is tangent to the circular path.
Considering the magnitude and direction, velocity is the cross product of angular velocity and the position vector
Where,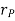 
is directed from axis to the point P
To find acceleration, differentiate velocity vector w.r.t time
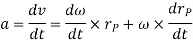
Here, the term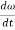 
refers to the angular acceleration 
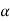of the rigid body
And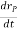 
is the velocity 
Hence,
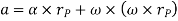
Where,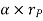 
is the tangential acceleration and 
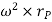is normal component of acceleration
Hence,
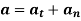
Magnitude of both components is given by,
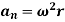
Tangential component refers to the time rate of change of velocity’s magnitude. Hence, if velocity of point P is increasing,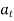 
is in same direction of 
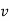, but if velocity of point P is decreasing, 
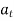is in direction opposite to that of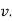 
The normal component of acceleration refers to time rate of change of the velocity’s direction. Hence, the direction of the normal component is always from point P towards the center O. Hence it is also called as centripetal acceleration.
General plane motion of a rigid body refers to a combination of translation and rotation motion.
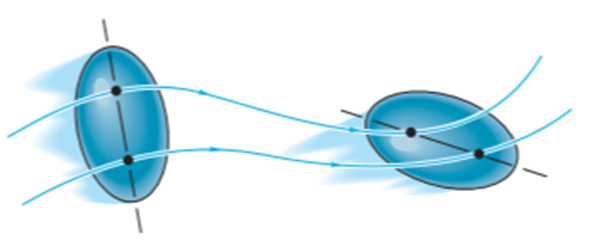
General planar motion refers to the simultaneous rotational and translational motion of a planar body in a 2-D plane.
General planar motion can be fully specified by knowing both the angular rotation of a line fixed in the body and the motion of any point on the body.
These motions can be related by using a rectilinear position coordinate s to locate the point along its path and an angular position coordinate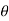 
to specify the orientation of the line. Then these two coordinates are related using the geometry of the problem. The following relation is found.
Differentiating the above equation, gives the relation between velocity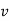 
and angular velocity 
.
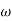Where,
Then again differentiating, it yields to the relation between acceleration 
and angular acceleration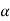 
Where,
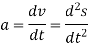
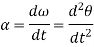
Chasle's theorem applies only to rigid body displacements. It says that for rigid bodies, any given displacement can be treated as equivalent to a translation (T) along an axis and a rotation (R) about the same axis.
Mathematically,
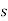is the resultant displacement
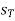is translational displacement
is the rotational displacement
It used to find the displacement equation of a rigid body in general plane motion.
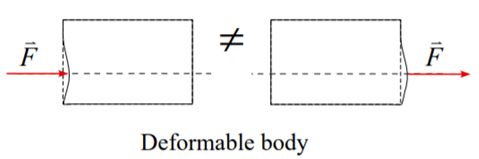
When a vector has constant magnitude and direction with a unique point of application of force, then the vector defining that force is termed as fixed vector.
When the body is supposed to be deformed by the action of constant force on a specified location, then the concept of fixed vector is used for the analysis.
Consider a body subjected to force defined by vector 
. If the force causes deformation in the body or a particle body, then the vector is said to be fixed vector. This vector is used in the analysis of a deformable bodies.
