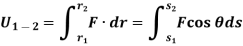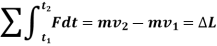UNIT 6
Work & Energy
When a particle subjected to force F undergoes a displacement in the direction of the force, the force F will do work on the particle.
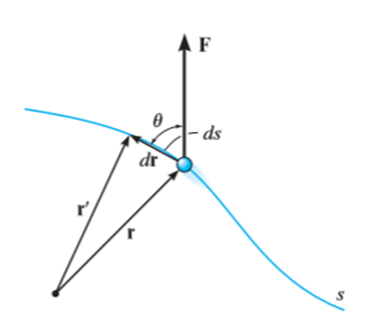
Consider a particle subjected to force F that causes the displacement of ds at an angle of 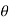 from the direction of force.
from the direction of force.
Let,
r = position vector of initial position
r’ = position vector of new position
dr = r’ – r = displacement whose magnitude is ds
The component of forces in the direction of motion that causes the particle to displacement is given as 
As we know,
Work = Force x displacement

Where, 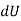 is the work done to displace the particle by ds
is the work done to displace the particle by ds
The work is a scalar quantity given by the dot product.
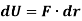
There are various types of work for different forces given below:
If a particle is subjected to variable force F that undergoes a displacement along its path with magnitude from  and
and 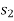 defined by the position vectors
defined by the position vectors 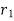 and
and  respectively and
respectively and  is the angle between the direction of force and the direction of displacement, as shown in figure, then the work done by the force F is given by
is the angle between the direction of force and the direction of displacement, as shown in figure, then the work done by the force F is given by
Where, F and  are defined as the function of position.
are defined as the function of position.
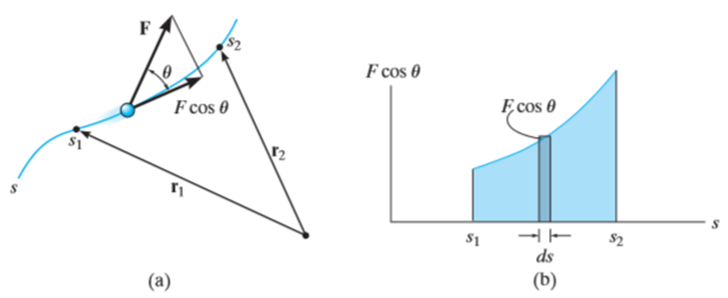
Then the area under this graph bounded by  and
and 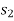 represents the total work. (Fig. b)
represents the total work. (Fig. b)
2. Work of constant force
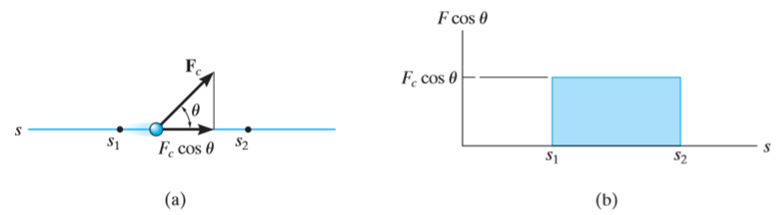
If a particle is subjected to constant force FC that undergoes a displacement along its path with magnitude from 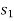 and
and 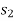 defined by the position vectors
defined by the position vectors 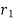 and
and  respectively and
respectively and 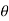 is the constant angle between the direction of force and the direction of displacement, as shown in figure, then the work done by the force FC is given by
is the constant angle between the direction of force and the direction of displacement, as shown in figure, then the work done by the force FC is given by
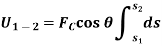

Then the area under this graph bounded by 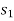 and
and 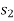 (rectangle) represents the total work. (Fig b)
(rectangle) represents the total work. (Fig b)
3. Work of weight
Consider a particle of weight W that moves along the path s from the position 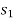 to
to 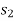 defined by the position vector
defined by the position vector  and
and 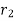 respectively.
respectively.

The displacement of a particle at any point intermediate on the path is given by

Since,

We have,
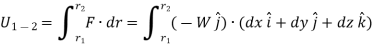
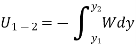
As weight is a constant force, hence,

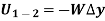
4. Work of spring force
Consider an elastic spring that is elongated by distance ds on the action of force FS as shown below.
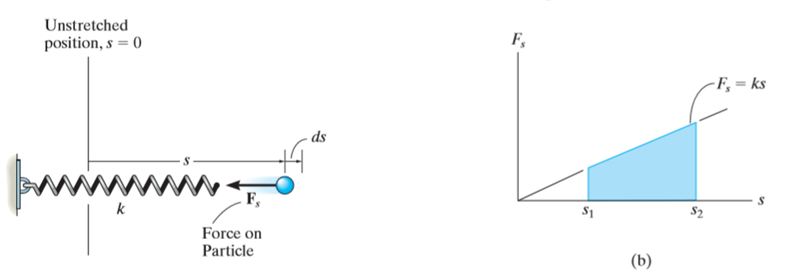
If a particle displaces from position 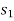 to
to 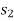 , then the work done is given by,
, then the work done is given by,
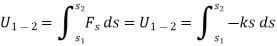
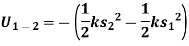
The trapezoidal region in the graph represents the total work done.
Principle of Work and Energy
The principle of work and energy states that, sum of the work done by all the forces acting on the particle is equal to the change in total energy (kinetic energy) of the particle.
Consider the particle located on the path that is defined relative to an inertial coordinate system as shown in figure below.
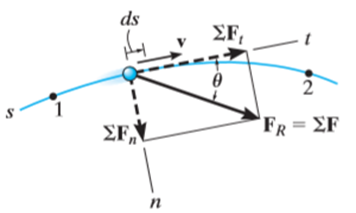
Let the particle has initial position  with speed
with speed 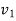 and final position
and final position  with speed
with speed 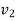
Let the particle has a mass m and is subjected to a system of external forces which is represented by the resultant force given below
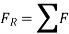
The equation of motion for the particle in the tangential direction is given by
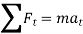
Applying the kinematic equation 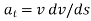 and integrating both sides
and integrating both sides



Where  and
and 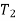 are the initial and final kinetic energies of the particle. Kinetic energy is always positive.
are the initial and final kinetic energies of the particle. Kinetic energy is always positive.
Using kinematics, the equation of motion for a particle of m is given by,
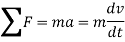

Integrating above equation between limits 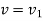 at
at 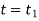 to
to  at
at 
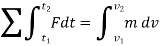
The term 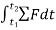 is referred as the linear impulse, while the term
is referred as the linear impulse, while the term  is change in linear momentum.
is change in linear momentum.
Since m is a positive scalar, the linear-momentum vector has the same direction as v.
Linear impulse is a vector quantity that measures the effect of a force during the time the force acts. As time is a positive scalar quantity, the impulse acts in the same direction as the force.
If the force is variable, the resulting impulse is given by

If the force is constant in magnitude and also in direction, the resulting impulse is given by

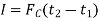
Graphically, magnitude of linear impulse is given by the area under the curve plotted on the force versus time plot.

Principle of impulse momentum states that sum of all the impulses applied to the particle in a time period of motion of a particle is equal to the change in momentum of the particle.
Mathematically,
Initial momentum + sum of impulses = Final momentum

Impact occurs when two bodies collide with each other in a very short period of time, resulting relatively huge (impulsive) forces to be exerted between the bodies.
Example: striking of a hammer on a nail, a golf club on a ball
There are two types on impact:
Central impact occurs when the direction of motion of the mass centers of the two colliding particles is along a line passing through the mass centers of the particles. This line is called the line of impact which is perpendicular to plane of contact.
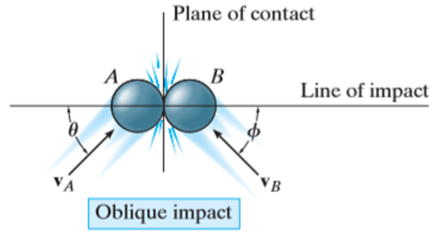
2. Oblique impact
When the motion of one or both of the particles make an angle with the line of impact, then the impact is said to be oblique impact.
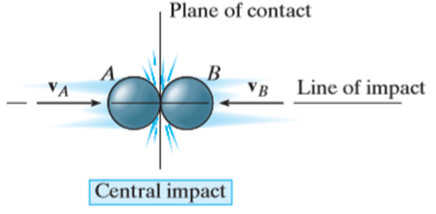
Consider two particles A and B involving the central impact of the shown in Fig. a
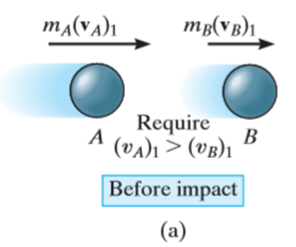
Let velocity of particle A is more than particle B.
During the collision the particles must be considered as deformable or nonrigid particles. The particles will undergo a period of deformation such that they exert an equal but opposite deformation impulse 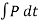 on each other.
on each other.
When the deformation becomes maximum, the relative motion of particle will become zero. Hence, the particle will move with same velocity v.

Then the particles will either return to their original shape or remain permanently deformed. This occurs after the period of restitution.
The equal but opposite restitution impulse 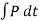 pushes the particles apart from each another, shown in fig d. In reality, the physical properties of any two bodies are such that the deformation impulse will always be greater than that of restitution.
pushes the particles apart from each another, shown in fig d. In reality, the physical properties of any two bodies are such that the deformation impulse will always be greater than that of restitution.
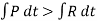
After the separation, the particles will have the final momenta as shown in Fig e.

Momentum for the system of particles is conserved as during the collision the internal impulses of deformation and restitution cancel each other.
Hence,
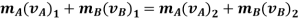
Applying impulse momentum equation for particle A during deformation phase (fig a, b and c), we get
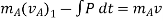
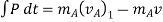
Now, applying impulse momentum equation for particle A during restitution phase (fig c, d and e), we get
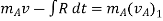
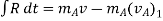
The ratio of the restitution impulse to the deformation impulse is called the coefficient of restitution.

Similarly, Coefficient of restitution can be established for particle B.
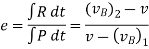
If velocity 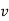 is unknown, then it can be eliminated from above equations and coefficient of restitution can be expressed in terms of the particle’s initial and final velocities
is unknown, then it can be eliminated from above equations and coefficient of restitution can be expressed in terms of the particle’s initial and final velocities
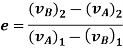
When, e = 1, the collision between the two particles is perfectly elastic. In perfectly elastic collision, the deformation impulse is equal and opposite to the restitution impulse. This is the ideal case and is impossible to achieve this case.
When e = 0, the collision between the two particles is perfectly plastic. In this case there is no restitution impulse so that after collision both particles couple or stick together and move with a common velocity.
Kinetic energy of a rigid body
Consider the rigid body as shown in Figure, which is represented here by a slab moving in the inertial x–y reference plane.

An arbitrary ith particle of the body, having a mass dm, is located a distance r from the arbitrary point P. If at the instant shown the particle has a velocity then the particle’s kinetic energy is

The kinetic energy of the entire body is determined by integrating above equations

Solving above equation when point P coincides with center of mass of the body G, we get

Where,
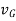 = velocity of center of mass or simply velocity of rigid body
= velocity of center of mass or simply velocity of rigid body
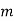 = mass of whole body
= mass of whole body
 = Mass moment of inertia of a body about an axis passing through center of mass G
= Mass moment of inertia of a body about an axis passing through center of mass G
 = angular velocity of a body
= angular velocity of a body
When a rigid body of mass m is subjected to either rectilinear or curvilinear translation motion, since 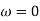 , the kinetic energy is given by
, the kinetic energy is given by
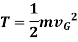

When a rigid body in rotation motion about an axis passing through center of mass G, then the kinetic energy is given by,

When a rigid body in rotation motion about a fixed axis passing through point O, then velocity of center of mass is given by,
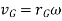
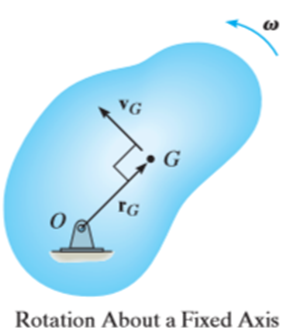
We have,
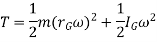
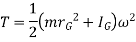
According to parallel axis theorem
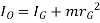

When a rigid body is subjected to general plane motion with an angular velocity 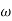 and its mass center has a velocity of
and its mass center has a velocity of 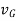 , then kinetic energy is given by
, then kinetic energy is given by
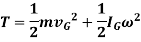
Work by a force for a rigid body
If an external variable force F acts on a body to move the body along the path s with displacement ds, then the work done is given by,
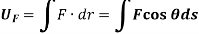
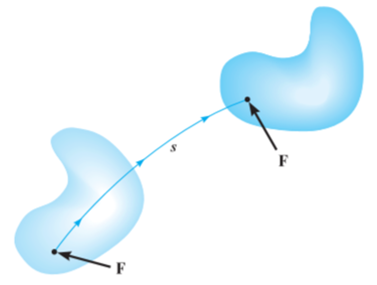
Where, 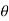 is the angle between the “tails” of the force and the differential displacement.
is the angle between the “tails” of the force and the differential displacement.
If an external constant force FC (constant in magnitude FC and direction 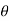 ) acts on a body to move the body along the path s with translation displacement s, then the work done is given by integrating above equation.
) acts on a body to move the body along the path s with translation displacement s, then the work done is given by integrating above equation.
Hence,
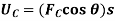
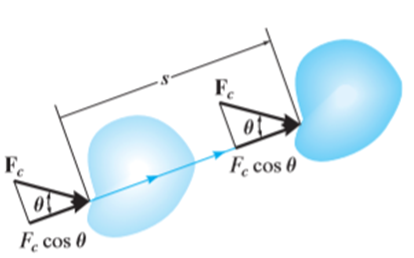
The weight W of a body does work when the center of mass G of a body undergoes a vertical displacement 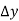 .
.


If a linear elastic spring is attached to a body, the spring force 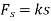 acting on the body does work when the spring either stretches or compresses from
acting on the body does work when the spring either stretches or compresses from 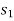 to a further position
to a further position 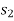 . In both cases the work will be negative since the displacement of the body is in the opposite direction to the force. The work is given by,
. In both cases the work will be negative since the displacement of the body is in the opposite direction to the force. The work is given by,
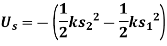
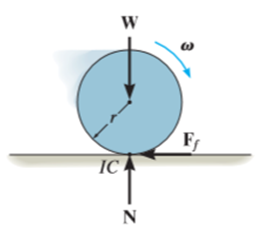
There are some external forces that do no work when the body is displaced. These forces act either at fixed points on the body, or they have a direction perpendicular to their displacement. Examples include the reactions at a pin support about which a body rotates, the normal reaction acting on a body that moves along a fixed surface, and the weight of a body when the center of gravity of the body moves in a horizontal plane.
Work by a couple moment for a rigid body
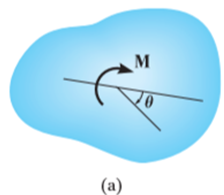
Consider the body shown in Fig a, which is subjected to a couple moment  that displaces the body through an angular displacement of
that displaces the body through an angular displacement of 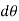 about an arbitrary point O.
about an arbitrary point O.
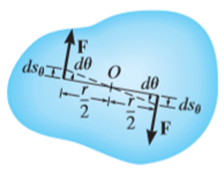
Then each force undergoes a displacement of 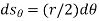 in the direction of the force.
in the direction of the force.
Hence work done is given by


When the body rotates in the plane through a finite angle  measured in radians, from
measured in radians, from 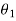 to
to 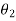 , the work of a couple moment is therefore given by
, the work of a couple moment is therefore given by
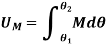
If the couple moment has constant magnitude, then
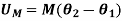
Principle of Work and Energy
By applying principle of work and energy to all the particles of the rigid body and adding all the results algebraically as energy is a scalar quantity, we get

Where,
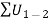 is work done by all the external forces and couple moments acting on the body
is work done by all the external forces and couple moments acting on the body
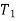 is the body’s total initial translational and rotational kinetic energy.
is the body’s total initial translational and rotational kinetic energy.
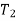 is the body’s total final translational and rotational kinetic energy.
is the body’s total final translational and rotational kinetic energy.
Consider a rigid body in general plane motion as shown in figure.

We have,

Taking moment at point A on both sides we get,
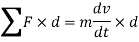
As the mass m of a rigid body and distance d of center of mass from point A is constant

The term 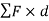 represents the total torque T on the particle at point A.
represents the total torque T on the particle at point A.
And  is the rate of change of moment of momentum.
is the rate of change of moment of momentum.
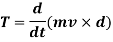
This is the moment of momentum equation.
It is derived from the moment of momentum principle, that states that the resulting torque acting on a rotating fluid is equal to the rate of chance of moment of momentum.

Integrating both sides
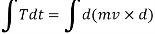
Where,
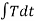 = angular impulse
= angular impulse
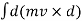 = change in angular momentum
= change in angular momentum
Assume the body is symmetric with respect to an inertial x–y reference plane.
The linear momentum of a rigid body is determined by summing vectorially the linear momenta of all the particles of the body given by
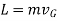
This equation states that the body’s linear momentum is a vector quantity having a magnitude 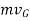 and direction is defined by the velocity
and direction is defined by the velocity  of the center of mass of the body
of the center of mass of the body
Now, consider the body with mass m, which is subjected to general plane motion with angular velocity 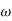 and linear velocity of center of mass given by
and linear velocity of center of mass given by  .
.
The angular momentum is given by,

When a rigid body is subjected to either rectilinear or curvilinear translation, since 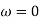 , angular momentum and linear momentum is given by
, angular momentum and linear momentum is given by

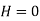

If the angular momentum is computed about some other point A, the “moment” of the linear momentum L must be found about the point.
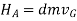
When a rigid body is rotating about a fixed axis passing through center of gravity, the linear momentum, and the angular momentum about G, are given by


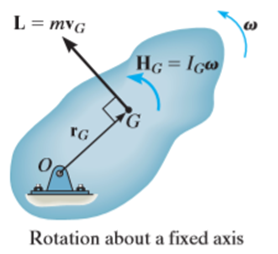
If the axis of rotation does not pass through center of mass G but through arbitrary point P, then
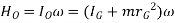
When a rigid body is subjected to general plane motion, the linear momentum, and the angular momentum about G, become
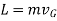

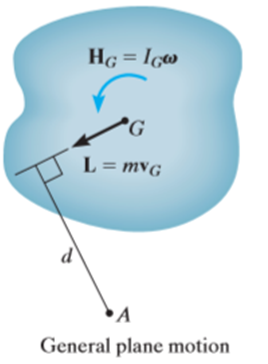
If the angular momentum is computed about point A, it is necessary to include the moment of L and about this point. In this case,

Principle of Linear Impulse and momentum
The equation of translational motion for a rigid body is given as
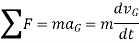
Since the mass of the body is constant,
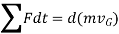
Integrating above equation between limits  at
at  to
to 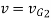 at
at 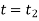
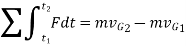
This equation is termed as the principle of linear impulse and momentum. It states that the sum of all the impulses created by the external force system which acts on the body during the time interval  to
to  is equal to the change in the linear momentum of the body during this time interval.
is equal to the change in the linear momentum of the body during this time interval.
Principle of Angular Impulse and momentum
When the body is a general plane motion,
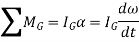
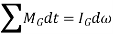
Integrating above equation between limits  at
at  to
to 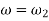 at
at 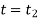
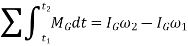
In a similar manner, for a body in rotation about a fixed axis passing through point O
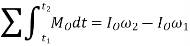

In general, if motion occurs in the x–y plane, the following three scalar equations can be written to describe the planar motion of the body.


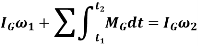
Conservation of Linear Momentum
If the sum of all the linear impulses acting on a system of connected rigid bodies is zero in a specific direction, then the linear momentum of the system is constant. Hence, conservation of linear momentum states that in such cases, initial linear momentum of a rigid body is equal to the final linear momentum of a rigid body.
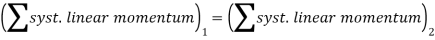
Or,
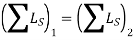
This equation is termed as the conservation of linear momentum.
Conservation of Angular Momentum
The angular momentum of a system of connected rigid bodies is conserved about the system’s center of mass G, or a fixed-point O, when the sum of all the angular impulses about these points is zero or appreciably small.
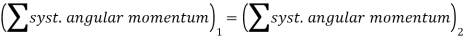
Or,
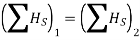
This equation is termed as the conservation of linear momentum.