Unit – 1
Definition of Partial Differential Equations
An equation containing the derivatives or differentials of one or more dependent variables with respect to one or more independent variables is called a differential equation.
Example: 
Notation: 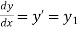
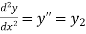
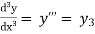
………………..
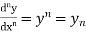
Order of a differential equation:
The order of the highest derivative involved in the differential equation i.e. how many times it is differentiated is called the order of the differential equation.
Degree of the differential equation:
The degree of the highest derivative involved in the differential equation after made free from radicals and fractions as far as derivatives are concerned i.e. power of the highest derivative is called the degree of the differential equation.
Example: 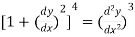 has order 2 and degree 3.
has order 2 and degree 3.
Types of Differential equations:

A differential equation involving derivatives with respect to single independent variables is called ordinary differential equation.
Example: 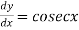
2. Partial Differential Equation:
A differential equation involving derivatives with respect to more than one independent variable is called partial differential equation.
Example: 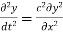
Linear and Non-linear differential equations:
A differential equation is linear if
Otherwise it is a non-linear equation.
Solution of differential equations:
A relation between the dependent variable and independent variables which satisfies the given differential equation is called the solution or the integral of the differential equation.
Example: The relation  is the solution of
is the solution of 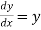 .
.
General solution, Particular solution and Singular solution:
Let  ….(i)
….(i)
Be an nth order ordinary differential equation.
General Solution: A solution of (i) which contain n arbitrary constants is called general solution.
Particular Solution: A solution of (i) which is obtained by substituting particular values to the one or more n arbitrary constants is called the particular solution.
Singular solution: A solution which cannot be obtained from the general solution.
Formation of Differential equation:
Working Rule: To construct the differential equation from the given family of curve in x and y containing n arbitrary constants.
Example1: Find the differential equation of all circles touching the y-axis at the origin?
The equation of the circle that touches y-axis at the origin is
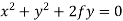 ….(i)
….(i)
Differentiating (i) with respect to x, we get
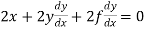
Or 
Or 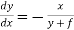
Or 
Or 
Or 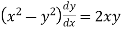
This is the required differential equation.
Example2: Form the differential equation of 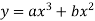 ?
?
Given curve 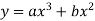
Differentiating the above curve with respect to x.

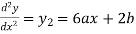
Multiplying both side by x.

Now, 
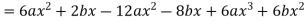 =0
=0
Hence the required equation is
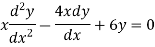
A partial differential equation (PDE) is an equation involving one or more partial derivatives of an (unknown) function, call it u, that depends on two or more variables, often time t and one or several variables in space. The order of the highest derivative is called the order of the PDE. Just as was the case for ODEs, second-order PDEs will be the most important ones in applications.
Just as for ordinary differential equations (ODEs) we say that a PDE is linear if it is of the first degree in the unknown function u and its partial derivatives. Otherwise we call it nonlinear.
The standard methods of solving the differential equations of the following
Types:
(i) Equations solvable by separation of the variables.
(ii) Homogeneous equations.
(iii) Linear equations of the first order.
(iv) Exact differential equations.
The differential equation of first order and first degree is namely:
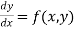
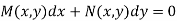
Example 1. Solve 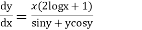 (UP,II 2008, U.P.B Pharm (C.O.)2005)
(UP,II 2008, U.P.B Pharm (C.O.)2005)
Solution. We have, 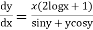
Seperating the variables we get
(sin y + y cos y ) dy ={ x (2 log x +1} dx
Integrating both the sides we get 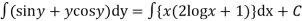

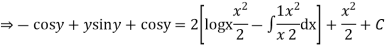

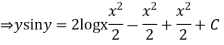
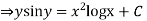
Example 2. Solve the differential equation
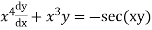 (A.M.I.E.T.E. Winter 2003)
(A.M.I.E.T.E. Winter 2003)
Solution. 

Put, 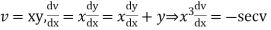
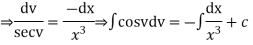
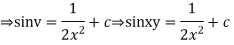
Linear Equations of the First Order
A linear partial differential equation of the first order, commonly known as Lagrange’s Linear equation is of the for4m
Pp + Qq = R (1)
Where, P, Q and R are functions of x, y, z. This equation is called a quast linear equation. When P, Q and R are independent of z it is known as linear equation.
Such asn equation is obtained by eliminating an arbitrary function  from
from 
where u,v are are some functions of x, y, z.
Differentiating (2) partially with respect to x and y
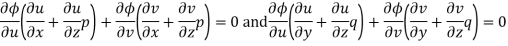
Eliminating 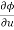 and
and  , we get
, we get 
Which simplifies to 
This is of the same form as (1)
Now suppose u = a and v=b, where a, b are constants, so that
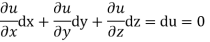
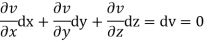
By cross multiplication we have,
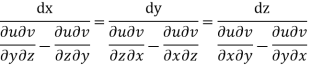

The solution of these equations are u = a and v = b
Therefore, 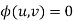 is the required solution of (1).
is the required solution of (1).
Thus to solve the equation Pp + Qq =R.
(i)form the subsidiary equations 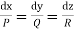
(ii) Solve these simultaneous equations
(iii) write the complete solution as 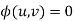 or u=f(v)
or u=f(v)
Example. Solve 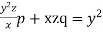 (Kottayam, 2005)
(Kottayam, 2005)
Solution. Rewriting the given equation as
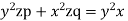
The subsidiary equations are 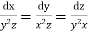
The first two fractions give 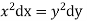
Integrating we get  n (i)
n (i)
Again the first and third fraction give xdx = zdz
Integrating, we get 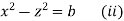
Hence from (i) and (ii), the complete solution is
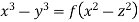
Example. Solve 
Solution. Here the subsidiary equations are 
Using multipliers x,y, and z we get each fraction = 
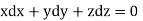 which on integration gives
which on integration gives 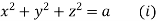
Again using multipliers l, m and n we get each fraction 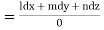
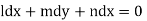 which on integration gives lx +my +nz = b (ii)
which on integration gives lx +my +nz = b (ii)
Hence from (i) and (ii) the required solution is 
Example. Solve 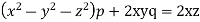
Solution. Here the subsidiary equations are 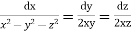
From the last two fractions, we have 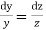
Which on integration gives log y = log z + log a or y/z=a (i)
Using multipliers x, y and z we have
Each fraction 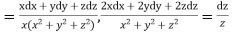
Which on integration gives 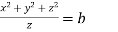
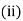
Hence from (i) and (ii) the required solution is 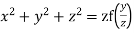
Linear Homogenous Partial Differential Equations Of Nth Order With Constant Coefficients
An equation of the type
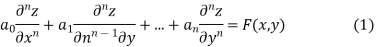
Is called a homogenous linear partial differential equation of nth order with constant coefficients
It is called homogenous because all the terms contain derivatives of the same order.
Putting, 
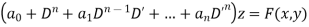

Rules for finding the particular integral
Given partial differential equation is
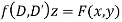
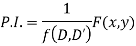
(i) When F (x, y)=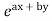
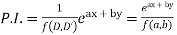 [Put D = a, D’ =b]
[Put D = a, D’ =b]
(ii) When F (x, y)=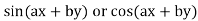
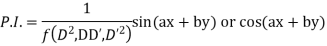
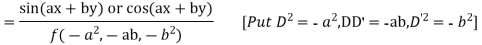
(iii) When F (x, y)=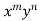
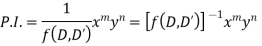

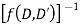 in ascending power of D or D’ and operate on
in ascending power of D or D’ and operate on 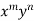 term by term.
term by term.
(iv) When = Any function F (x, y)

Resolve 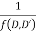 into partial fractions
into partial fractions
Considering f(D, D’) as a function of D alone
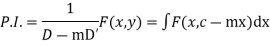
Where c is replaced by y + mx after integration
Case 1. When R.H.S =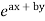
Example 1. Solve 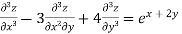
Solution. 
Given equation in symbolic form is
(D3-3D2 D'+4D'3)z=ex+2y
It’s A.E. is 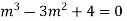 where m = -1,2, 2
where m = -1,2, 2
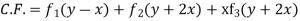
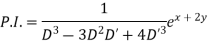
Put, D=1,D’=2
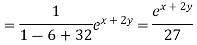
Hence complete solution is

Case II. When R.H.S = 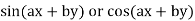
Example 2. Solve 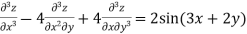
Solution. 
Putting
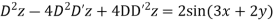
A.E. is 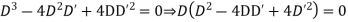
Put 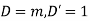

C.F. is 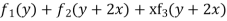
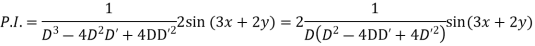
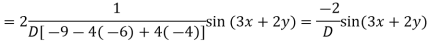

General solution is 
Example 3. Solve 
A.E. is 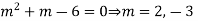
C.F. = 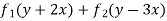

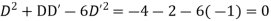
It is a case of failure.
Now, 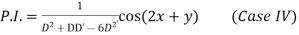
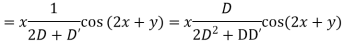
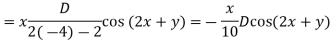
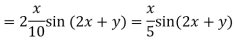
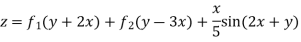
Case III. When R.H.S. = 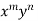
Example 4. Find the general integral of the equation

Solution. 
With 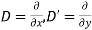 the given equation can be written in the form
the given equation can be written in the form
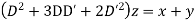
Writing D = m and D’=1the auxiliary equation is


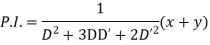
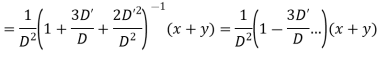
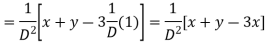

Hence the complete solution is 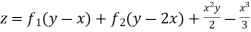
Case IV. When R.H.S. = Any Fraction
Example 5. Solve 
Solution. 
A.E. is 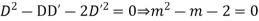
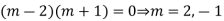

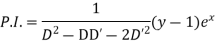



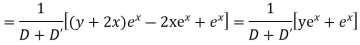
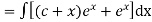
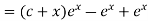
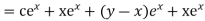

Hence complete solution is 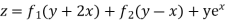
Non Homogeneous Linear equations
The linear differential equations which are not homogeneous are called non Homogeneous Linear equations.
For example

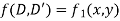
Its solution,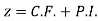
Complementary function : let the non Homogeneous equation be
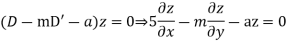
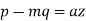
The Lagrange’s subsidiary equations are
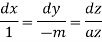
From first two relations we have, -mdx = dy
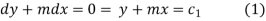
And some first and third relation,


From (1) and (2) we have 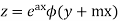
Similarly the solution of 
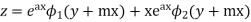
Example. Solve 
Solution. Equation is written as
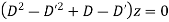
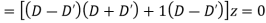

Hence the solution is
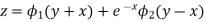
Particular integral
Case 1. 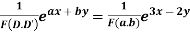
Example. 
The complementary function is


Hence the complete solution is 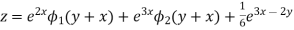
Case 2. 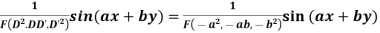
Example. Solve 
Solution. 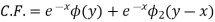
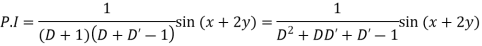
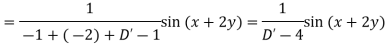
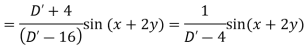

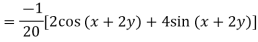
Hence the solution is 
Case 3. 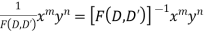
Example. Solve 
Solution. 




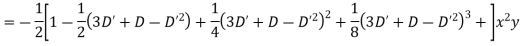
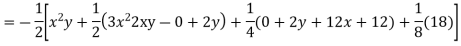
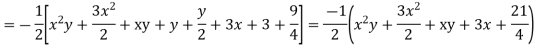
Hence the complete solution is 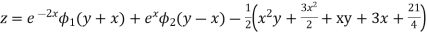
Linear differential equation of second order with constant coefficients
The general form of the linear differential equation of second order is
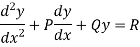
Where P and Q are constants and R is a function of x or constant.
Differential operator
Symbol D stands for the operation of differential i.e.
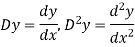
 stands for the operation of integration.
stands for the operation of integration.
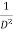 stands for the operation of integration twice.
stands for the operation of integration twice.
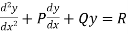 can be written in the operator form.
can be written in the operator form.
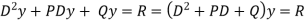
Complete solution - Complementary function + Particular integral
Let us consider a linear differential equation of the first order
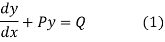
Its solution is 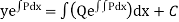
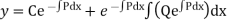

Where,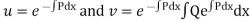
(i)Now differentiating 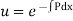 with respect to x we get
with respect to x we get 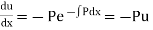
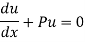

Which shows that y = cu is the solution of 
(ii) Differentiating 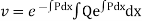 with respect to x, we get
with respect to x, we get
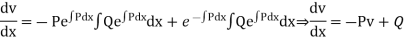
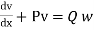 hich shows that y = v is the solution of
hich shows that y = v is the solution of 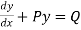
Solution of the differential equation (1) is (2) consisting of two parts i.e. cu and v. cu is the solution of the differential equation whose right hand side is zero. cu is known as complementary function. Second part of (2) is v free from any arbitrary constant and is known as particular integral.
Complete solution = complementary function + particular integral

Method for finding the complementary function
(1) In finding the complementary function, R.H.S of the given equation is replaced by zero.
(2) Let 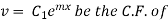
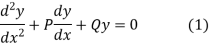
Putting the values of y, 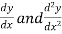 (1) then
(1) then 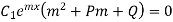
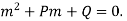 It is called Auxiliary equation.
It is called Auxiliary equation.
(3) Solve the auxiliary equation.
Case 1. Roots, real and different.
If 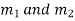 are the roots then the C.F. is
are the roots then the C.F. is

Equation (1) can be written as

Replacing 
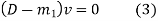

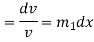


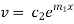
From (3) 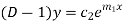
This is the linear differential equation.


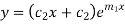
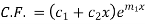
Example 1. Solve 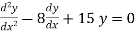
Solution. Given equation can be written as

Here auxiliary equation is 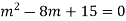
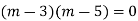
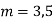
Hence the required solution is
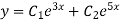
Example 2. Solve. 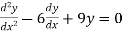
Solution. Given equation can be written as
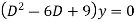
A.E. is 
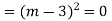

Hence the required solution is
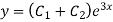
Example 3. Solve 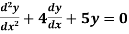
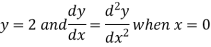
Solution. Here the auxiliary equation is
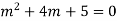
Its root are 
The complementary function is
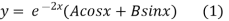
On putting y = 2 and x = 0 in (1) we get
2 =A
On putting A = 2 in (1) we have
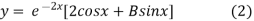
On Differentiating (2) we get
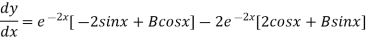


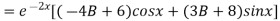
But, 
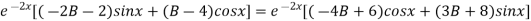
On putting x = 0, we get
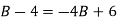
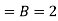
(2) becomes, 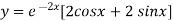
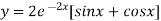
PDE’s are usually specified through a set of boundary or initial conditions. A boundary condition expresses the behaviour of a function on the boundary (border) of its area of definition. An initial condition is like a boundary condition, but then for the time-direction. Not all boundary conditions allow for solutions, but usually the physics suggests what makes sense. Let me remind you of the situation for ordinary differential equations, one you should all be familiar with, a particle under the influence of a constant force.
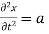 which leads to
which leads to
 , and
, and
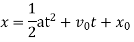
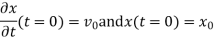
These are linear initial conditions (linear since they only involve xx and its derivatives linearly), which have at most a first derivative in them. This one order difference between boundary condition and equation persists to PDE’s. It is kind of obviously that since the equation already involves that derivative, we can not specify the same derivative in a different equation.
A solution of a PDE in some region R of the space of the independent variables is a function that has all the Partial derivatives appearing in the partial differential equation in some domain D containing R, and satisfies the partial differential equation everywhere in R.
Often one merely requires that the function is continuous on the boundary of R, has doors derivatives in the interior of R, and satisfies the partial differential equation in the interior of R. Letting R lie in D simplifies the situation regarding derivatives on the boundary of R, which is the same on the boundary as it is in the interior of R.
In general, the totality of solutions of a partial differential equation is very large. For example the functions
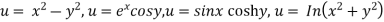
Which are entirely different from each other, are solutions of (3), as you may verify. We shall see later that the unique solution of a partial differential equation corresponding to a given physical problem will be obtained by the use of additional conditions arising from the problem. For instance this may be the condition that the solution u assume given values on the boundary of the region R (boundary conditions). Or when time t is one of the variables, u may be prescribed at t =0 (initial conditions)
The method of d'Alembert provides a solution to the one-dimensional wave equation
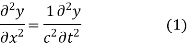
that models vibrations of a string.
The general solution can be obtained by introducing new variables 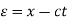 and
and 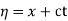 , and applying the chain rule to obtain
, and applying the chain rule to obtain


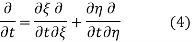
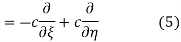
Using (4) and (5) to compute the left and right sides of (3) then gives

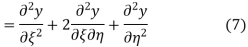

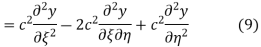
respectively, so plugging in and expanding then gives
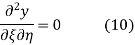
This partial differential equation has general solution
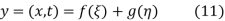
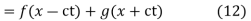
where f and g are arbitrary functions, with f representing a right-traveling wave and g a left-traveling wave.
The initial value problem for a string located at position 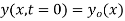 as a function of distance along the string x and vertical speed
as a function of distance along the string x and vertical speed 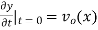 can be found as follows. From the initial condition and (12),
can be found as follows. From the initial condition and (12),
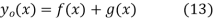
Taking the derivative with respect to 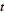 then gives
then gives


and integrating gives
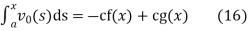
Solving (13) and (16) simultaneously for f and g immediately gives
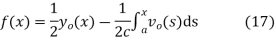
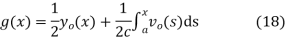
so plugging these into (13) then gives the solution to the wave equation with specified initial conditions as
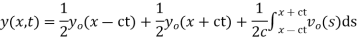
Example. Find the deflection of a vibrating string of unit length having fixed ends with initial velocity zero and initial deflection f (x) =k (sinx –sin2x)
Solution. By d’Alembert’s method, the solution is
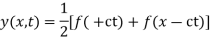

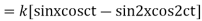
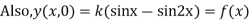
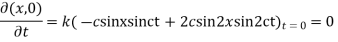
i.e., the given boundary corrections are satisfied.
One dimensional heat flow
Let heat flow along a bar of uniform cross section in the direction perpendicular to the cross section. Take one end of the bar as origin and the direction of the heat flow is along x axis.
Let the temperature of the bar at any time t at a point x distance from the origin be u(x,t). Then the equation of one-dimensional heat flow is 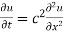
Example 1. A rod of length 1 with insulated sides is initially at a uniform temperature u. Its ends are suddenly cooled to 0° Celsius and are kept at that temperature. Prove that the temperature function u (x, t) is given by
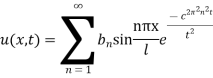
Where  is determined from the equation.
is determined from the equation.
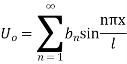
Solution. Let the equation for the conduction of heat be
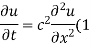
Let us assume that u = XT, where X is a function of x alone and T that of t alone.

Substituting these values in (1) we get 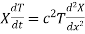
i.e. 
Let each side be equal to a constant 


And 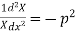
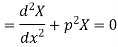
Solving (3) and (4) we have

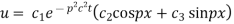
Putting x = 0, u = 0 in (5), we get
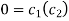

(5) becomes 
Again putting x = l, u =0 in (6), we get
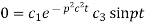



Hence (6) becomes 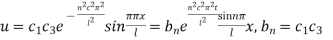
This equation satisfies the given conditions for all integral values n. Hence taking n = 1, 2, 3,…, the most general solution is

By initial conditions 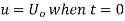
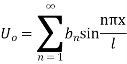
Example 2. Find the solution of
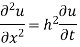
For which u ( 0, t) = u (l.t) =0 =sin 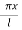 bi method of variable separable.
bi method of variable separable.
Solution. 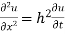
In example 10 the given equation was
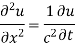
On comparing (1) and (2) we get 
Thus solution of (1) is

On putting x =0
u =0 in (3) we get

(3) reduced to

On putting x = l and u =0 in (4) we get
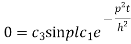

Now (4) is reduced to

On putting t = 0, u = 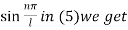

This equation will be satisfied if
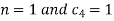
On putting the values of 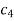 and n in (5) we have
and n in (5) we have
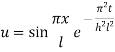
Example 3. The ends A and B of a rod 20 cm long having the temperature at 30 degree Celsius and at 80 degree Celsius until steady state prevails. The temperature of the ends are changed to 40 degree Celsius and 60 degree Celsius respectively. Find the temperature distribution in the rod at time t.
Solution. The initial temperature distribution in the rod is

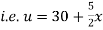
And the final distribution (i.e. steady state) is
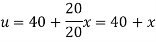
To get u in the intermediate period, reckoning time from the instant when the end temperature were changed we assumed

Where 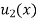 is the steady state temperature distribution in the rod (i.e. temperature after a sufficiently long time) and
is the steady state temperature distribution in the rod (i.e. temperature after a sufficiently long time) and 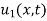 is the transient temperature distribution which tends to zero as t increases.
is the transient temperature distribution which tends to zero as t increases.
Thus, 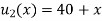
Now 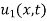 satisfies the one dimensional heat flow equation
satisfies the one dimensional heat flow equation

Hence u is of the form
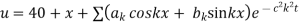
Since 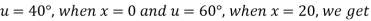
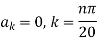
Hence 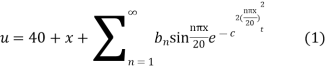
Using the initial condition i.e.
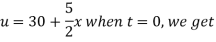
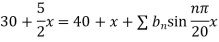
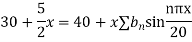
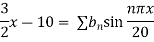
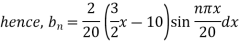
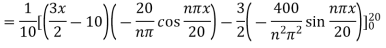

Putting this value of  n (1), we get
n (1), we get
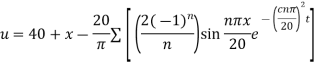
Q.1] Determine the solution of one dimensional heat Equation

Under the boundary condition 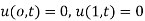 and
and 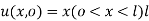 being the length of rod
being the length of rod
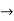 The equation of heat flow is
The equation of heat flow is 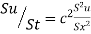
Since the temp of two ends of rod are zero its solution is of form
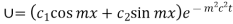
Using initial condition
i] 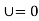 when
when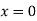 we get
we get


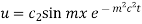
ii] 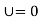 when
when
 where
where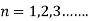
Hence the general solution is
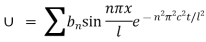
 We get solution as
We get solution as

Equation of vibrating string
Consider an elastic string tightly stretched between two points O and A. Let O be the origin and OA as x axis. On giving a small displacement to the string perpendicular to its length (parallel to the y axis). Let y be the displacement at the point P (x, y) at any time. The wave equation
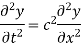
Example. Obtain the solution of the wave equation
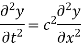
Using the method of separation of variables.
Solution. 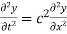
Let y = XT where X is a function of x only and T is a function of t only.
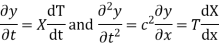
Since T and X are functions of a single variable only.
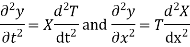
Substituting these values in the given equation we get

By separating the variables we get

(Each side is constant since the variables x and y are independent)

Auxiliary equations are
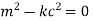
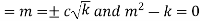
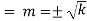
Case 1. If k>0

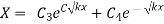
Case 2. If k<0
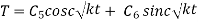

Case 3. If k =0
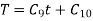
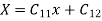
These are the three cases depending upon the particular problems. Hare we are dealing with wave motion (k<0)
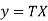
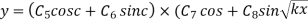
Example. Find the solution of the wave equation

Such that 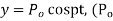 is a constant) when x = 1 and y = 0 when x =0
is a constant) when x = 1 and y = 0 when x =0
Solution. 
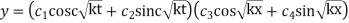
Put y = 0, when x = 0
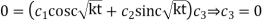
(2) is reduced to


Put  when x=1
when x=1
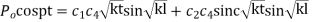
Equating the coefficient of sin and cos on both sides


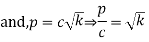
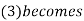
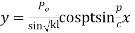
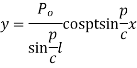
Example. The vibrations of an elastic string is governed by the partial differential equation

The length of the string is π and the ends are fixed. The initial velocity is zero and the initial deflection is u (x, 0)=2 (sinx + sin3x). Find the deflection u (x,t) of the vibrating string for t≥0.
Solution.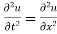

On putting x =0, u = 0 in (1) we get
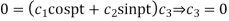
On putting 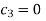 in (1) we get
in (1) we get

On putting  and u =0 in (2) we have
and u =0 in (2) we have

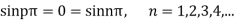

on substituting the value of p in (2) we get
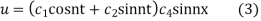
on differentiating (3(,w.r.t t we get

On putting  in (4) we have
in (4) we have

On putting 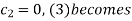

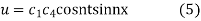
Given u (x, 0) = 2 (sin x+ sin3x)
On putting t = 0 in (5) we have

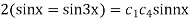
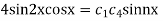
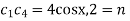
On substituting the value of 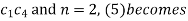

Method of separation of variables
In this method, we assume that the dependent variable is the product of two functions, each of which involves only one of the independent variables. So to ordinary differential equations are formed.
Example 1. Using the method of separation of variables, solve
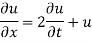

Solution. 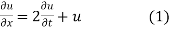
Let, u = X(x). T (t). (2)
Where X is a function of x only and T is a function of t only.
Putting the value of u in (1), we get
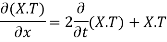
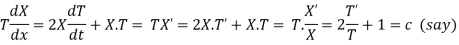
(a) 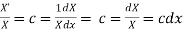
On integration log X = cx + log a = log 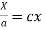

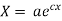
(b)
On integration 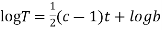
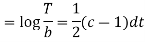


Putting the value of X and T in (2) we have
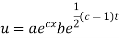
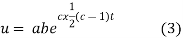
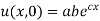
But, 
i.e. 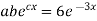

Putting the value of a b and c in (3) we have
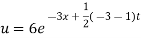
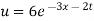
Which is the required solution.
Example 2. Use the method of separation of variables to solve equation
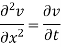
Given that v = 0 when t→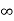 as well as v =0 at x = 0 and x = 1.
as well as v =0 at x = 0 and x = 1.
Solution. 
Let us assume that v = XT where X is a function of x only and T that of t only

Substituting these values in (1), we get

Let each side of (2) equal to a constant 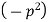
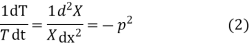

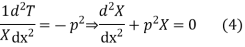
Solving (3) and (4) we have
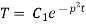
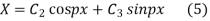
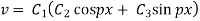
Putting x = 0, v = 0 in (5) we get

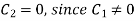
On putting the value of 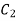 in (5) we get
in (5) we get
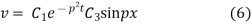
Again putting x = l, v= 0 in (6) we get
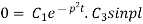
Since 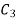 cannot be zero.
cannot be zero.


Inputting the value of p in (6) it becomes
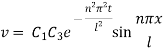
Hence, 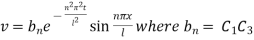
This equation satisfies the given condition for all integral values of n. Hence taking n = 1, 2, 3,… the most general solution is

Example. Using the method of separation of variables, solve 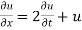 Where
Where 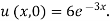
Solution. Assume the given solution 
Substituting in the given equation, we have
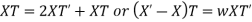
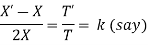

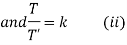
Solving (i) 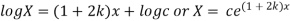
From (ii) 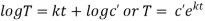
Thus 
Now, 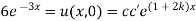

Substituting these values in (iii) we get
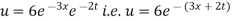
Which is the required solution
The axis of Laplace plane is coplanar with, and between,
(a) The polar axis of the parent planet's spin, and
(b) The orbital axis of the parent planet's orbit around the Sun.
The Laplace plane arises because the equatorial oblateness of the parent planet tends to cause the orbit of the satellite to precess around the polar axis of the parent planet's equatorial plane, while the solar perturbations tend to cause the orbit of the satellite to precess around the polar axis of the parent planet's orbital plane around the Sun. The two effects acting together result in an intermediate position for the reference axis for the satellite orbit's precession.
The mean plane occupied by the orbit of a satellite during a precession cycle; the plane normal to the orbital precession pole of the satellite.
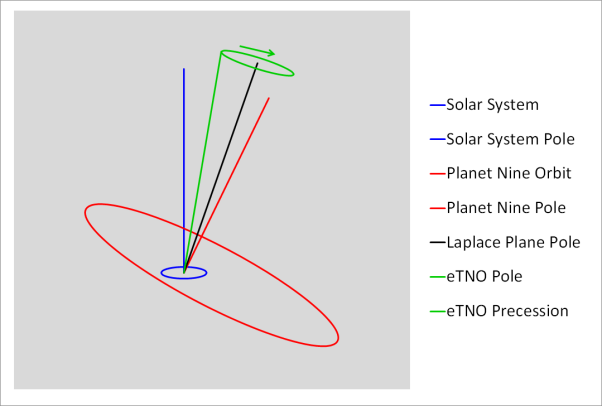
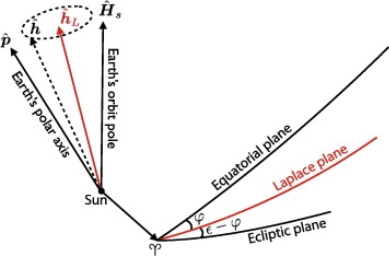
In effect, this is the plane normal to the orbital precession pole of the satellite. It is a kind of "average orbital plane" of the satellite, around which the instantaneous orbital plane of the satellite precesses, and to which it has a constant additional inclination.
In most cases, the Laplace plane is very close to the equatorial plane of its primary planet (if the satellite is very close to its planet) or to the plane of the primary planet's orbit around the Sun (if the satellite is far away from its planet). This is because the strength of the planet's perturbation on the satellite's orbit is much stronger for orbits close to the planet, but drops below the strength of the Sun's perturbation for orbits farther away.
Examples of satellites whose Laplace plane is close to their planet's equatorial plane include the satellites of Mars and the inner satellites of the giant planets. Examples of satellites whose Laplace plane is close to their planet's orbital plane include Earth's Moon and the outer satellites of the giant planets. Some satellites, such as Saturn's Iapetus, are situated in the transitional zone and have Laplace planes that are midway between their planet's equatorial plane and the plane of its solar orbit.
So the varying positions of the Laplace plane at varying distances from the primary planet can be pictured as putting together a warped or non-planar surface, which may be pictured as a series of concentric rings whose orientation in space is variable: the innermost rings are near the equatorial plane of rotation and oblateness of the planet, and the outermost rings near its solar orbital plane. Also, in some cases, larger satellites of a planet (such as Neptune's Triton) can affect the Laplace planes of smaller satellites orbiting the same planet.
Spherical polar coordinates
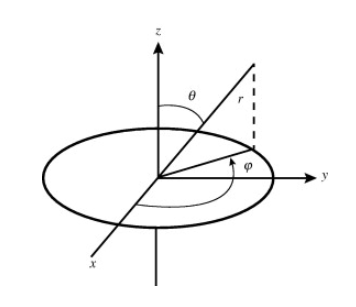
In spherical polar coordinates, the coordinates are r, where r is the distance from the origin,
where r is the distance from the origin, 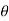 is the angle from the polar direction (on the earth, colatitude, which is 90° - latitude), and
is the angle from the polar direction (on the earth, colatitude, which is 90° - latitude), and  the azimuthal angle (longitude). It is customary to align the polar direction with the cartesian co-ordinate z and to measure
the azimuthal angle (longitude). It is customary to align the polar direction with the cartesian co-ordinate z and to measure 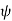 from a zero ( our Greenwich meridian) along the +x direction, with the direction of
from a zero ( our Greenwich meridian) along the +x direction, with the direction of 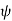 such that the +y direction is at
such that the +y direction is at 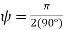
Therefore, points with a given value of r lie on a sphere of radius r centred at the origin and points of given 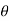 lie on a cone with vertex at the origin, axis in the z direction and an opening angle of rotation
lie on a cone with vertex at the origin, axis in the z direction and an opening angle of rotation  . Points of given
. Points of given 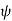 lie on a half plane which extends from the polar axis to infinity in the direction given by
lie on a half plane which extends from the polar axis to infinity in the direction given by 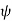 . In order for co-ordinate sets and arbitrary spatial points to be unambiguously related, we need to restrict angle of r to
. In order for co-ordinate sets and arbitrary spatial points to be unambiguously related, we need to restrict angle of r to  , with
, with 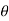 in the range
in the range  and within
and within 
The equations connecting the two sets of coordinates are
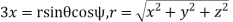
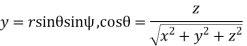

Notice that equation gives formulas for  rather than for
rather than for  . When we convert
. When we convert 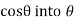 we must use the principal value of
we must use the principal value of 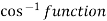 so as to obtain a result to within the range
so as to obtain a result to within the range 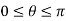 . For we must be even more careful, as a range for the principal value of
. For we must be even more careful, as a range for the principal value of 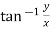 is only of length π while the range of
is only of length π while the range of 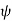 is of length 2π. We must choose the value of
is of length 2π. We must choose the value of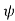 that is in the azimuthal quadrant consistent with the individual signs of x and y.
that is in the azimuthal quadrant consistent with the individual signs of x and y.
Circular cylindrical coordinates
Circular cylinder coordinates use the plane polar coordinates 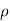 and
and 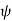 (in place of x and y) and the z Cartesian coordinates. The variable
(in place of x and y) and the z Cartesian coordinates. The variable 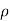 is the distance of co-ordinate point from the z. Cartesian axis, and
is the distance of co-ordinate point from the z. Cartesian axis, and 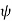 is its azimuthal angle. The range of these coordinates are
is its azimuthal angle. The range of these coordinates are 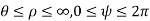 , and of course
, and of course 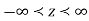 . Thus, points of given
. Thus, points of given 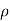 lie on a cylinder about the z axis of radius
lie on a cylinder about the z axis of radius 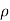 , points of given
, points of given  lie on a half plane extending from the entire z axis to infinity in the
lie on a half plane extending from the entire z axis to infinity in the 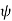 direction and points of given z lie on the plane with that value of z.
direction and points of given z lie on the plane with that value of z.
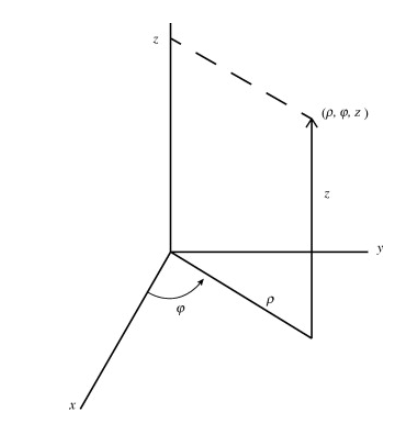
The conversion formulas between circular cylindrical and cartesian coordinates are
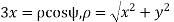
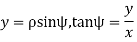
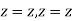
The co-ordinate  has the same definition as for spherical polar coordinates, and just as there, it must be identified as the value of
has the same definition as for spherical polar coordinates, and just as there, it must be identified as the value of 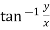 consistent with the individual signs of x and y. We have used
consistent with the individual signs of x and y. We have used 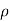 (not r) as the co-ordinate denoting distance from the z axis, we are reserving r to always mean distance from the origin and will reserve
(not r) as the co-ordinate denoting distance from the z axis, we are reserving r to always mean distance from the origin and will reserve  for the axle distance defined here.
for the axle distance defined here.
Bessel functions
Bessel equation
The differential equation
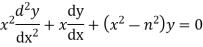
Is called the Bessel Differential equation and particular solutions of the equation are called Bessel function of order n.
General solution of Bessel’s equation is

Solution of Bessel’s equation
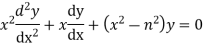
Let 
So that, 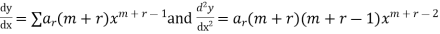
Substituting these values in the equation we have



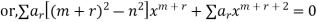
Equating the coefficient of 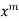 to zero, we get
to zero, we get
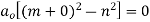 , (r=0)
, (r=0)
 ,
, 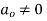
Equating the coefficient of 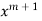 (r=1)
(r=1)
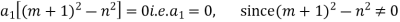
Equating the coefficient of  to zero, to find the relation in uccessive coefficient we get
to zero, to find the relation in uccessive coefficient we get
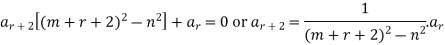
Therefore, 
If r=0, 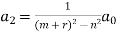
If r = 2, 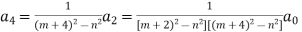 and so on
and so on
On substituting the values of the coefficients in (2) we have

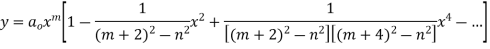
Fo m = n

Where  is an arbitrary constant
is an arbitrary constant
For m = -n
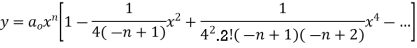
Bessel functions 
The Bessel Function is 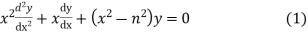
Solution of (1) is

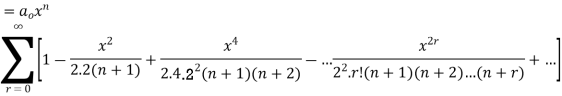
Where 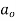 is an arbitrary constant
is an arbitrary constant
If 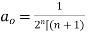
The above equation is called Bessel function denoted by 
Thus, 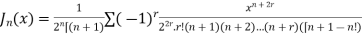
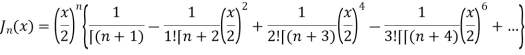
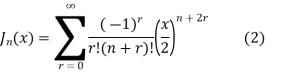
If n = 0, 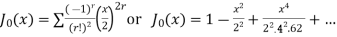
If n= 1, 
We draw the graphs of these btwo functions. Both the functions are oscillary with a varrying period aqnd a decreasing amplitude.
Replace n by –n in (2), we get
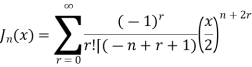
Example 1. Prove that  , where n is a positive integer.
, where n is a positive integer.
Solution. 


\On putting r = n + k


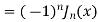
Example 2, Prove that
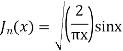
Solution. We know that
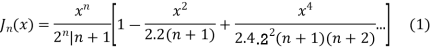
Substituting 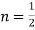 in (1) we obtain
in (1) we obtain
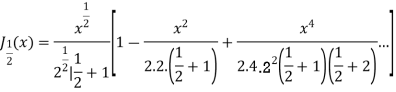
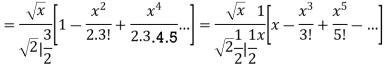

Recurrence Formula
Formula I. 
Formula II,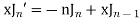
Formula III.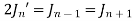
Formula IV.
Formula V.
Formula VI.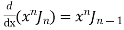
Example. Prove that 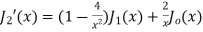 where
where 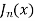 is the Bessel function of first kind.
is the Bessel function of first kind.
Solution. By recurrence formula II
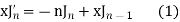
On putting n = 2, in (1) we have 
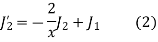
By recurrence formula I
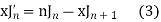
From (1) and (3) we have 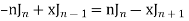
On putting n = 1, 
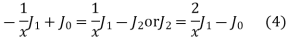
Putting the value of  from (4) in (2) we get
from (4) in (2) we get


Example. Prove that

Solution. We know that

Integrating above relation we get

On taking n = 2 in (1) we have
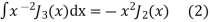
Again, 
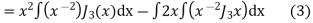
Putting the value of  from (2) in (3) we get
from (2) in (3) we get

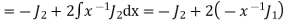
On using (1) again when n = 1
Hence, 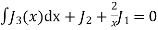
Legendre functions
Legendre’s Equation
The differential equation 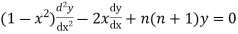 is known as Legendre’s equation. The above equation can also be written as
is known as Legendre’s equation. The above equation can also be written as
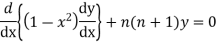
Legendre’s Polynomial 
Definition.
The Legendre’s Equation is
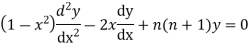
The solution of the above equation in the series of descending powers of x is
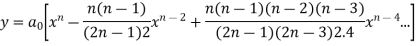
Where  is an arbitrary constant.
is an arbitrary constant.
Now if n is a positive integer and 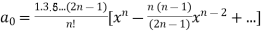
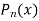 is called the Legendre’s function of the first kind.
is called the Legendre’s function of the first kind.
Legendre’s Function of the second kind i.e. 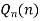
Another solution of Legendre equation
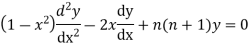
Where n is a positive integer.

If we take, 
The above equation is called  so that
so that
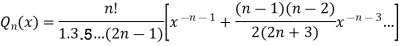
The series for 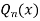 is a non- terminating series.
is a non- terminating series.
General solution of Legendre’s Solution
Since 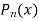 and
and  are two independent solutions for Legendre’s Equation therefore the most general solution of Legendre’s equation is
are two independent solutions for Legendre’s Equation therefore the most general solution of Legendre’s equation is

Where A and B are two arbitrary constants.
Example 1. Let 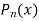 be the Legendre polynomial of degree n. Show that for any function f (x), for which the nth derivative is continuous.
be the Legendre polynomial of degree n. Show that for any function f (x), for which the nth derivative is continuous.
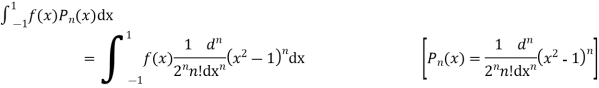
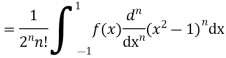
Integrating by parts, we have
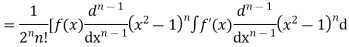
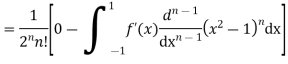
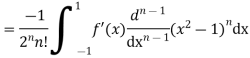
Again integrating by parts, we have


Integrating (n-2) times, by parts we get
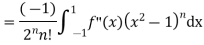
Legendre Polynomial
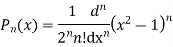
If n = 0, 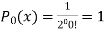
If n = 1, 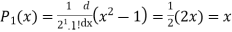
If n = 2, 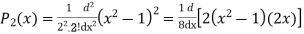
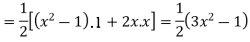
Similarly, 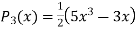


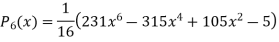

Where,  if n even.
if n even.
 if n is odd.
if n is odd.
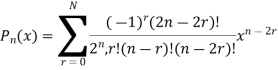
Either  is in the last term.
is in the last term.
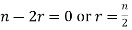 (n is even)
(n is even)
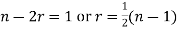 (n is odd)
(n is odd)
Example. Express  in terms of Legendre Polynomials,
in terms of Legendre Polynomials,
Solution. Let
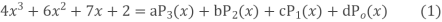
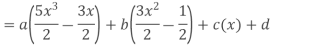
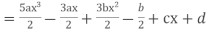
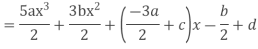
Equating the coefficients of like powers of x we have
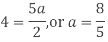
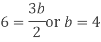
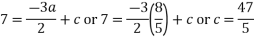
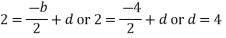
Putting the values of a, b, c, d in (1) we get
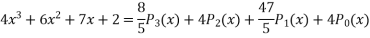
The 1 D diffusion equation
The famous diffusion equation also known as heat equation, reads
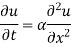
Where u (x, t) is the unknown function to be solved for, x is a co-ordinate in space, and t is time. The coefficient 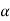 is the diffusion coefficient and determines how fast u changes in time. Quick short form for the diffusion equation is
is the diffusion coefficient and determines how fast u changes in time. Quick short form for the diffusion equation is 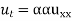
Compare to the wave equation  which looks very similar but the diffusion equation features solutions that are very different from those of the wave equation. Also the diffusion equation makes quite different demands to the numerical methods.
which looks very similar but the diffusion equation features solutions that are very different from those of the wave equation. Also the diffusion equation makes quite different demands to the numerical methods.
Typical diffusion problems may experience rapid change in the very beginning but then the evolution of u becomes slower and slower. The solution is usually very smooth and after sometime one cannot recognise the initial shape of u. This is in sharp contrast to solutions of the wave equation where the initial shape is preserved – the solution is basically a moving initial condition. The standard wave equation  has solutions that propagates with speed c forever, without changing shape, while the diffusion equation converges to a stationary solution
has solutions that propagates with speed c forever, without changing shape, while the diffusion equation converges to a stationary solution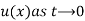 . In this limit,
. In this limit,  and
and  is governed by
is governed by  . This stationary limit of the diffusion equation is called the Laplace Equation and rises in a very wide range of applications throughout the sciences.
. This stationary limit of the diffusion equation is called the Laplace Equation and rises in a very wide range of applications throughout the sciences.
It is possible to solve for u (x, t) using a explicit scheme, but the time step restrictions soon become much less favourable 10 for an explicit scheme for the wave equation. And of more importance, since the solution u of the diffusion equation is very smooth and changes slowly, small x steps are not convenient and not required by accuracy as the diffusion process converges to a stationary state.
Example. Solve the equation with boundary conditions 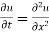 u (x ,0) = 3 sin nπx, u (0 ,t) and u (1, t) =0, where 0 < x < 1, t > 0.
u (x ,0) = 3 sin nπx, u (0 ,t) and u (1, t) =0, where 0 < x < 1, t > 0.
Solution. The solution of the equation 

When x = 0, 
(Ii) becomes 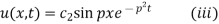
When x = 1, 
Ie., P = nπ
(iii) reduces to 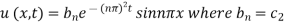
Thus the general solution of (i) is 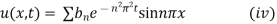
When t=0, 3 sin nπx = u (0, t) = 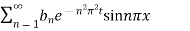
Comparing both sides 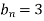
Hence from (iv), the desired solution is
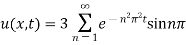
Example. Solve the differential equation  for the conduction of the heat along a road with out radiation subject to the following conditions
for the conduction of the heat along a road with out radiation subject to the following conditions
(i) u is not infinite for 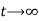
(ii) 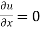 for x = 0 and x = l,
for x = 0 and x = l,
(iii) u = lx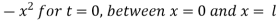
Solution. Substituting u =X(x) T(t) in the given equation we get
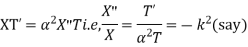
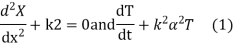
Their solutions are 
If  is changed to
is changed to  the solutions are
the solutions are
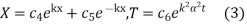
If  , the solutions are
, the solutions are 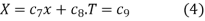
In (3),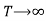 for
for  therefore, u also → i.e. , the given condition (i) is not satisfied so we reject the solution (3) while (2) and (4), satisfy the condition.
therefore, u also → i.e. , the given condition (i) is not satisfied so we reject the solution (3) while (2) and (4), satisfy the condition.
Applying the condition (ii) to (4) we get 
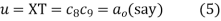
From (2) 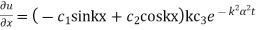
Applying the condition (ii) we get 
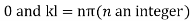
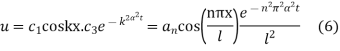
Thus the general solution being the sum of (5) and (6) is

Now using the condition (iii), we get

This being the expansion of  as a half range cosine in (0,l), we get
as a half range cosine in (0,l), we get
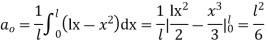
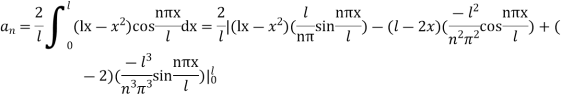

Hence taking n = 2m, the required solution is
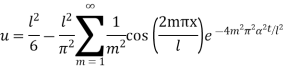
Example. The ends A and B of a rod 20 cm long have the temperature at 30 degree Celsius and 80 degree Celsius and 10 study state prevails. The temperature of the ends are changed to 40 degree Celsius and 60 degree Celsius respectively. Find the temperature distribution in the rod at time t.
Solution. Let the heat equation be 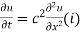
In steady state condition, u is independent of time and depends on x only, (i) reduces to
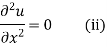
Its solution is u = a + bx
Since u = 30 for x = 0 and u = 80 for x = 20, therefore a= 30, b = (80-30)/20=5/2
Thus the initial conditions are expressed by
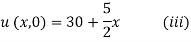
The boundary conditions are 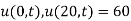
Using (ii) the steady state temperature is

To find the temperature u in the intermediate period,
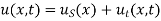
Where 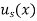 is the steady state temperature distribution of the form (iv) and
is the steady state temperature distribution of the form (iv) and  is the transition temperature distribution which decreases to zero as t increases.
is the transition temperature distribution which decreases to zero as t increases.
Since 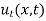 satisfies one dimensional heat equation
satisfies one dimensional heat equation

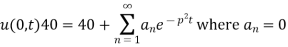
(iv) reduces to
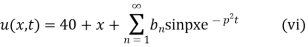

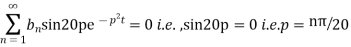
Thus (vi) becomes 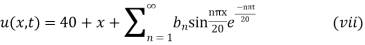
Using (iii) 
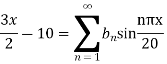
Where 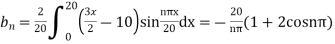
Hence from (vii) the desired solution is
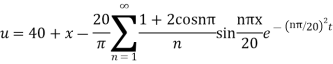
References
1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.
2. N.P. Bali and Manish Goyal, A text book of Engineering Mathematics, Laxmi Publications.
3. P. G. Hoel, S. C. Port and C. J. Stone, Introduction to Probability Theory, Universal Book Stall.
4. S. Ross, A First Course in Probability, 6th Ed., Pearson Education India,2002.