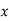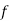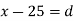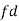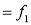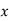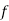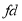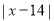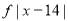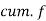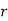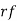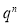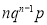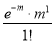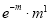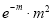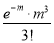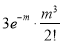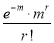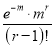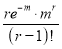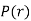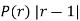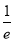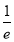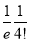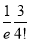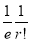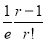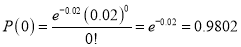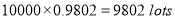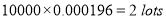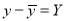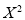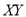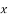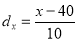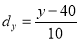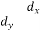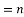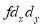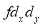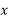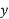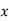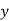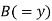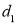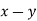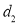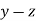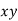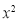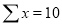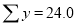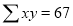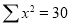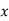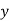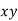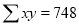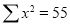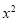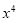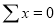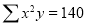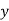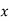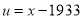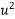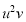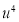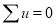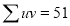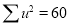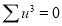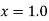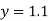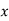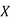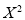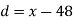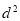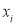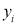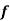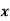Unit – 3
Basic Statistics
STATISTICS is a branch of science dealing with the collection of data, organizing, summarizing, presenting and analyzing data and drawing valid conclusions and thereafter making reasonable decisions on the basis of such analysis.
Collection of Data
The collection of data constitution the starting point of any statistical investigation. Data may be collected for each and every unit of the whole lot (population), for it would ensure greater accuracy. But completer enumeration is prohibitively expensive and time consuming. As such out of a very large number of items, a few of them (a sample) are selected and conclusions drawn on the basis of this sample are taken to hold for the population.
Classification of data
The data collected in the course of an inquiry is not in an easily assimilable form. As such, its proper classification is necessary for making intelligent references. The classification is done by dividing the raw data into a convenient number of groups according to the values of the variable and finding the frequency of the variable in each group.
Let us for example, consider the raw data relating to marks obtained in Mechanics by a group of 64 students:
79 84 65 78 67 80 62 78 | 88 75 75 82 73 73 67 89 | 75 82 87 75 81 57 97 61 | 60 68 74 91 72 88 78 75 | 93 90 62 77 63 78 85 95 | 71 62 95 69 76 62 76 60 | 59 88 78 74 75 76 65 79 | 85 76 63 68 85 53 71 83 |
This data can conveniently be grouped and shown in a tabular form as follows:
It would be seen from the above table that there is one student getting marks between 50-54, two students getting marks between 55-59, nine students getting marks between 60-64 and so on. Thus the 64 figure have been put into only 10 groups, called the classes. The width of the class is called the class interval and the number in that interval is called the frequency. The mid-point or the mid-value of the class is called the class mark. The above table showing the classes and the corresponding frequencies is called a frequency table. Thus a set of raw data summarized by distributing it into a number of classes along with their frequencies is known as a frequency distribution.
While forming a frequency distribution, the number of classes should not ordinarily exceed 20, and should not, in general, be less than 10. As far as possible, the class intervals should be of equal width.
Cumulative frequency:
In some investigations we require the number of items less than a certain value. We add up the frequencies of the classes upto that value and call this number as the cumulative frequency. In the above table, the third column shows the cumulative frequencies, i.e., the number of students, getting less than 54 marks, less than 59 marks and so on.
Graphical Representation:
A convenient way of representing a sample frequency distribution is by means of graphs. It gives to the eyes the general run of the observations and at the same time makes the raw data readily intelligible. We give below the important types of graphs in use:
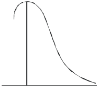
(i) Histogram
A histogram is drawn by erecting rectangles over the class intervals, such that the areas of the rectangles are proportional to the class frequencies. If the class intervals are of equal size, the height of the rectangles will be proportional to the class frequencies themselves (Fig 25.1).
(ii) Frequency Polygon
A frequency polygon for an ungrouped data can be obtained by joining points plotted with the variable values as the abscissae and the frequencies as the ordinates, For a grouped distribution, the abscissae of the points will be the mid-values of the class intervals. In case the intervals are equal the frequency polygon can be obtained by joining the middle points of the upper sides of the rectangles of the histogram by straight lines (shown by dotted lines in Fig 25.1). if the class intervals become very small, the frequency polygon takes the form of a smooth curve called the frequency curve.
(iii) Cumulative frequency curve-ogive
Very often, it is desired to show in a diagrammatic form, not the relative frequencies in the various intervals, but the cumulative frequencies above or below a given value. For example, we may wish to read off from a diagram the number or proportions of people whose income is not less than any given amount, or proportion of people whose height does not exceed any stated valued. Diagrams of this type are known as cumulative frequency curves or ogives. These are two kinds ‘more than’ and typically they look somewhat a long drawn S (Fig. 25.2).
Example:
Draw the histogram, frequency polygon, frequency curve and the ogive ‘less than’ and ‘mite than’ from the following distribution of marks obtained by 49 students:
Class (Maths group) | Frequency (No. of students) | Cumulative frequency | |
Less than | More than | ||
5-10 10-15 15-20 20-25 25-30 30-35 35-40 40-45 | 5 6 15 10 5 4 2 2 | 5 11 26 36 41 45 47 49 | 49 44 38 23 13 8 4 2 |
Solution: In Fig. 25.1, the rectangles show the histogram; the dotted polygon represents the frequency polygon and the smooth curve is the frequency curve.
The ogives ‘less than’ and ‘more than’ are shown in fig (25.2).
Average or Measures of Central tendency
An average is a value which is representative of a set of data. Average value may also be termed as measures of central tendency. There are five types may also be termed as measures of central tendency. There are five types of averages in common.
Arithmetic Mean
If 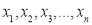 are n numbers, then their arithmetic mean (A.M) is defined by
are n numbers, then their arithmetic mean (A.M) is defined by

If the number  occurs
occurs  times,
times, 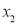 occurs
occurs 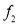 times and so on, then
times and so on, then

This is known as direct method.
Example 1: Find the mean of 20, 22, 25, 28, 30.
Solution:

Example 2: Find the mean of the following:
Numbers | 8 | 10 | 15 | 20 |
Frequency | 5 | 8 | 8 | 4 |
Solution:
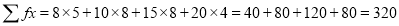

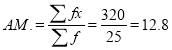
(b) Shortcut method
Let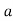 be the assumed mean, d the deviation of the variate
be the assumed mean, d the deviation of the variate 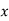 from
from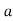 . Then
. Then
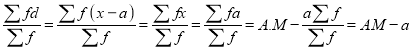


Example 2: Find the arithmetic mean for the following distribution:
Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
Frequency | 7 | 8 | 20 | 10 | 5 |
Solution:
Let assumed mean 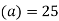
Class | Mid-value
| Frequency
|
|
|
0-10 10-20 20-30 30-40 40-50 | 5 15 25 35 45 | 7 8 20 10 5 | -20 -10 0 10 5 | -140 -80 0 100 100 |
Total |
|
| 50 | -20 |
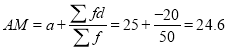
(c) Step deviation method
Let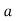 be the assumed mean,
be the assumed mean, 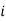 the width of the class interval and
the width of the class interval and

Median
Median is defined as the measure of the central item when they are arranged in ascending or descending order of magnitude.
When the total number of the items is odd and equal to say 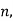 then there are two middle items, and so the mean of the values of
then there are two middle items, and so the mean of the values of  and
and  items is the median.
items is the median.
Example :
Find the median of 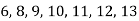
Solution:
Total number of items =7
The middle item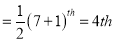
Median=Value of the 4th item=10
For grouped data, Median
Where 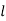 is the lower limit of the median class,
is the lower limit of the median class, 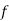 is the frequency of the class,
is the frequency of the class, 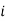 is the width of the class- interval, F is the total of all the preceeding frequencies of the median – class and N is total frequency of the data.
is the width of the class- interval, F is the total of all the preceeding frequencies of the median – class and N is total frequency of the data.
Example :
Find the value of Median from the following data.
No.of days for which absent (less than) | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
No.of students | 29 | 224 | 465 | 582 | 634 | 644 | 650 | 653 | 655 |
Solution: The given cumulative frequency distribution will first be converted into ordinary frequency as under
Class Interval | Cumulative frequency | Ordinary frequency |
0-5 5-10
15-20 20-25 25-35 30-35 35-40 40-45 | 29
465 582 634 644 650 653 655 | 29=29 224-29=195 465-224= 582-465=117 634-582=52 644-634=10 650-644=6 653-650=3 655-653=2 |
Median= size of or 327.5th item
or 327.5th item
327.5th item lies in 10-15 which is the median class.
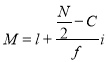
Where 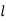 stands for lower limit of median class,
stands for lower limit of median class,
N stands for the total frequency,
C stands for the cumulative frequency just preceding the median class,
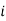 stands for class interval
stands for class interval
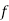 stands for frequency for the median class.
stands for frequency for the median class.
Median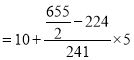
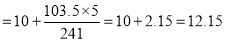
Mode
Mode is defined to be the size of the variable which occurs most frequently.
Example:
Find the mode of the following items:
0, 1, 6, 7, 2, 3, 7, 6, 6, 2, 6, 0, 5, 6, 0.
Solution:
6 occurs 5 times and no other item occurs 5 or more than 5 times, hence the mode is 6.
For grouped data, Mode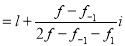
where 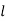 is the lower limit of the modal class,
is the lower limit of the modal class,  is the frequency of the modal class,
is the frequency of the modal class,  is the width of the class,
is the width of the class, 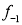 is the frequency before the modal class and
is the frequency before the modal class and 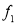 of the frequency after the modal class.
of the frequency after the modal class.
Emperical formula
Mean – Mode = 3 [Mean – Median]
Example:
Find the mode from the following data:
Age | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 | 30-36 | 36-42 |
Frequency | 6 | 11 | 25 | 35 | 18 | 12 | 6 |
Solution:
Age | Frequency | Cumulative frequency |
0-6 6-12 12-18
24-30 30-36 36-42 | 6 11 25 35 12 6 | 6 17 42 77 95 107 113 |
Mode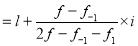
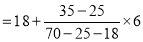
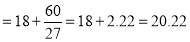
Geometric Mean
If  be n values of variates x, then the geometric mean
be n values of variates x, then the geometric mean

Example.
Calculate the harmonic mean of 4, 8, 16.
Solution:
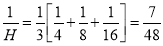

Average deviation or Mean Deviation
It is the mean of the absolute values of the deviations of a given set of numbers from their arithmetic mean.
If 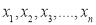 be a set of numbers with frequencies
be a set of numbers with frequencies 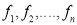 respectively. Let
respectively. Let 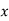 be the arithmetic mean of the numbers
be the arithmetic mean of the numbers  ,then
,then
Mean deviation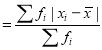
Example:
Find the mean deviation of the following frequency distribution.
Class | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 |
Frequency | 8 | 10 | 12 | 9 | 5 |
Solution:
Let 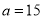
Class | Mid value
| Frequency
|
|
|
|
|
0-6 6-12 12-18 18-24 24-30 | 3 9 15 21 27 | 8 10 12 9 5 | -12 -6 0 6 12 | -96 -60 0 54 60 | 11 5 1 7 13 | 88 50 12 63 65 |
Total |
| 44 |
| -42 |
| 278 |
Mean
Average deviation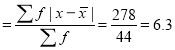
MOMENTS
The rth moment of a variable x about the mean x is usually denoted by is given by
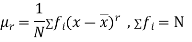
The rth moment of a variable x about any point a is defined by

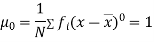
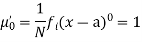

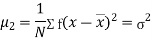
Relation between moments about mean and moment about any point:
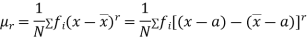
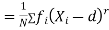 where
where and
and 
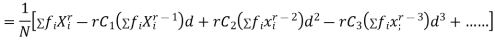
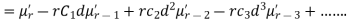
In particular
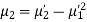


Note. 1. The sum of the coefficients of the various terms on the right‐hand side is zero.
2. The dimension of each term on right‐hand side is the same as that of terms on the left.
MOMENT GENERATING FUNCTION
The moment generating function of the variate 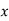 about
about 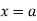 is defined as the expected value of
is defined as the expected value of  and is denoted by
and is denoted by  .
.
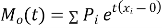

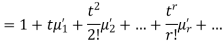
where  , ‘ is the moment of order
, ‘ is the moment of order  about
about 
Hence  coefficient of
coefficient of  or
or 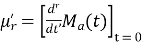
again  )
) 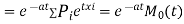
Thus, the moment generating function about the point  moment generating function about the origin.
moment generating function about the origin.
SKEWNESS:
Skewness denotes the opposite of symmetry. It is lack of symmetry. In a symmetrical series, the mode, the median, and the arithmetic average are identical.
Coefficient of skewness 
KURTOSIS: It measures the degree of peakedness of a distribution and is given by Measure of kurtosis.


Negative skewness Positive skewness A: Mesokurtic B: Leptokurtic
C: Playkurtic
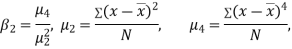
If  , the curve is normal or mesokurtic.
, the curve is normal or mesokurtic.
If 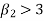 , the curve is peaked or leptokurtic.
, the curve is peaked or leptokurtic.
If  , the curve is flat topped or platykurtic
, the curve is flat topped or platykurtic
Example
The first four moments about the working mean 28.5 of a distribution 0.294, 7.144, 42.409 and 454.98. Calculate the moments about the mean. Also evaluate 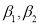 and comment upon the skewness and kurtosis of the distribution.
and comment upon the skewness and kurtosis of the distribution.
Solution:
The first four moments about the arbitrary origin 28.5 are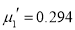 ,
,  ,
,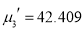 and
and 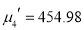 .
.

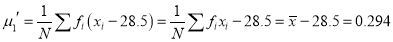 or
or 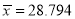

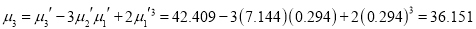
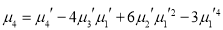
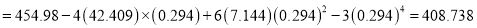
Now 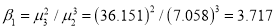
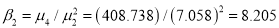

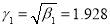 which indicates considerable skewness of the distribution.
which indicates considerable skewness of the distribution.
 which shows that the distribution is leptokurtic.
which shows that the distribution is leptokurtic.
Example
Calculate the median, quartiles and the quartile coefficient of skewness from the following data:
Weight (lbs) | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 | 140-150 |
No. of Persons | 12 | 18 | 35 | 42 | 50 | 45 | 20 | 8 |
Solution
Here total frequency 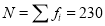 .
.
The cumulative frequency table is
Weight (lbs) | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 | 140-150 |
| 12 | 18 | 35 | 42 | 50 | 45 | 20 | 8 |
| 12 | 30 | 65 | 107 | 157 | 202 | 222 | 230 |
Now  item which lies in 110-120 group.
item which lies in 110-120 group.
 Median or
Median or 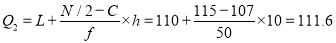
Also 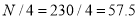 i.e.
i.e.  is
is 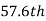 or
or 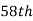 item which lies in 90-100 group.
item which lies in 90-100 group.

Similarly,  i.e.,
i.e.,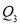 is
is 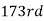 item which lies in 120-130 group.
item which lies in 120-130 group.

Hence quartile coefficient of skewness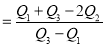
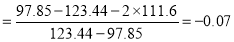 (approx..)
(approx..)
A probability distribution is a arithmetical function which defines completely possible values &possibilities that a random variable can take in a given range. This range will be bounded between the minimum and maximum possible values. But exactly where the possible value is possible to be plotted on the probability distribution depends on a number of influences. These factors include the distribution's mean, SD, Skewness, and kurtosis.
Binomial Distribution:
Binomial Distribution 
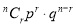
To find the probability of the happening of an event once, twice, …., r times… exactly in n trials.
Let the probability of the happening of an event A in one trial be  and its probability of not happening be
and its probability of not happening be 
We assume that there are n trials and the happening of the event 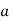 is
is times and it’s not happening n-r times.
times and it’s not happening n-r times.
This may be shown as follows

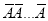
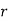 times
times  times ….(1)
times ….(1)
A indicates its happening, 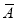 its failure and
its failure and 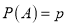 and
and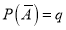 .
.
We see that (1) has the probability
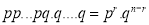 …. (2)
…. (2)
r times n-r times
Clearly (1) is merely one order of arranging r A’s
The probability of (1)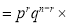 Number of different arrangements of
Number of different arrangements of 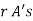 and
and 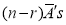 .
.
The number of different arrangements of 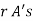 and
and 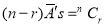
 Probability off the happening of an event
Probability off the happening of an event  times
times 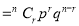
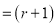 th term of
th term of 

If  , probability of happening of an event 0 times
, probability of happening of an event 0 times 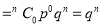
If  , probability of happening of an event 1 times
, probability of happening of an event 1 times 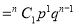
If 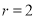 , probability of happening of an event 2 times
, probability of happening of an event 2 times 
If 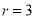 , probability of happening of an event 3 times
, probability of happening of an event 3 times 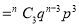
These terms are clearly the successive terms in the expansion of 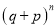 . Hence it is called Binomial distribution.
. Hence it is called Binomial distribution.
Example
If on an average one ship in every ten is wrecked, find the probability that of 5 ships expected to arrive, 4 at least will arrive safely.
Solution:
Out of 10 ships, one ship is wrecked.
i.e., Nine ships out of ten ships are safe. P(safety) 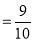
P(At least 4 ships out of 5 ships are safe) 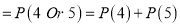
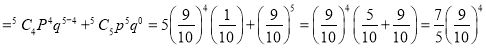
Example
The overall percentage of failures in a certain examination is 20. If six candidates appear in the examination, what is the probability that at least five pass the examination?
Solution:
Probability of failures 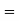
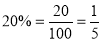
Probability 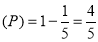
Probability of at least five pass 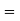 P(5 or 6)
P(5 or 6)
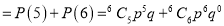
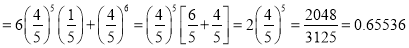
Example
The probability that a man aged 60 will live to be 70 is 0.65. What is the probability that out of 10 item, now 60, at least 7 will live to be 70?
Solution
The probability that a man aged 60 will live to be 70
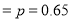

Number of men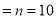
Probability that at least 7 men will live to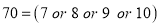
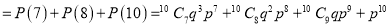
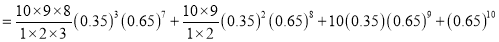
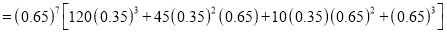
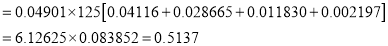
Example
A die is thrown 8 times and it is required to find the probability that 3 will show (i) Exactly 2 times
(ii) At least seven times (iii) At least once.
Solution:
The probability of throwing 3 in a single trial =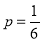
The probability of not throwing 3 in a single trial 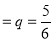
(i) P (getting 3 exactly 2 times)=P (getting 3, at 7 or 8 times) 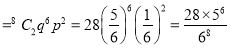
(ii) P (getting 3, at least seven times)=P (getting 3, at 7 or 8 times) 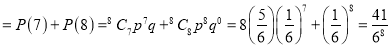
(iii) P (getting 3 at least once)
= P (getting 4, at 1 or 2 or 3 or 4 or 5 or 6 or 7 or 8 times)
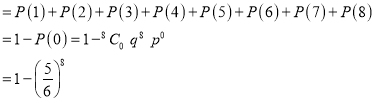
Example:
Assuming that 20% of the population of a city are literate, so that the chance of an individual being literate is 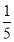 and assuming that 100 investigators each take 10 individuals to see whether they are literate, how many investigators would you expect 3 or less were literate.
and assuming that 100 investigators each take 10 individuals to see whether they are literate, how many investigators would you expect 3 or less were literate.
Solution 
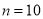
P (3 or less) = P (0 or 1 or 2 or 3 )

Required number of investigators
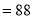 approximately
approximately
Mean of Binomial Distribution
Successes | Frequency |
|
0 |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
… | …. | …. |
4 |
|
|
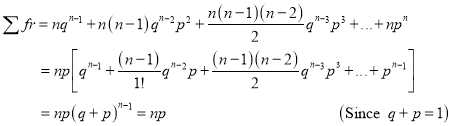
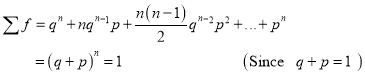
Hence Mean
Standard Deviation of Binomial Distribution
Successes | Frequency |
|
0 |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
…. | …. | … |
n |
|
|
We know that 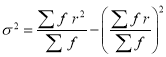 ….(1)
….(1)
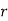 is the deviation of items (successes) from 0.
is the deviation of items (successes) from 0.

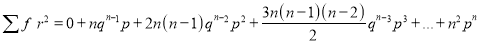

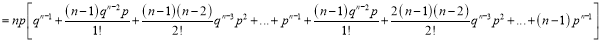
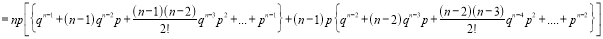

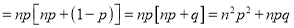
Putting these values in (1), we have
Variance

Hence for the binomial distribution, Mean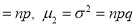
Example:
A die is tossed thrice. A success is getting 1 or 6 on a toss. Find the mean and variance of the number of successes.
Solution:

Mean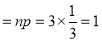
Variance
Recurrence relation for the binomial distribution
By Binomial distribution 

On dividing (2) by (1), we get

Poisson Distribution:
Poisson distribution is a particular limiting form of the Binomial distribution when p or (q) is very small and n is large enough.
Poisson distribution is 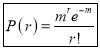
Where m is the mean of the distribution.
Proof:
In Binomial distribution
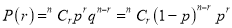 { Since mean
{ Since mean }
}
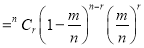 (
(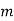 is constant)
is constant)

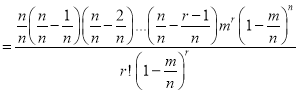
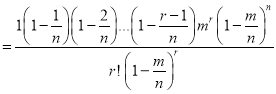
Taking limits, when n tends to infinity
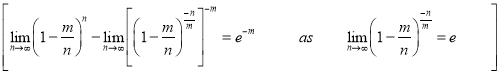
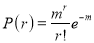

Mean of Poisson Distribution

Successes | Frequency |
|
0 |
| 0 |
1 |
|
|
2 |
|
|
3 |
|
|
… | … | …. |
r |
|
|
… | … | …. |
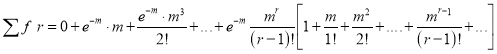
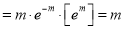
Mean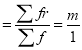

Standard Deviation of Poisson Distribution

Successes | Frequency | Product | Product |
0 |
| 0
| 0 |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
… | …. | …. | … |
r |
|
|
|
… | …. | … | … |
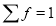


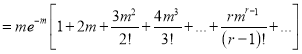

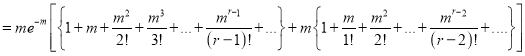

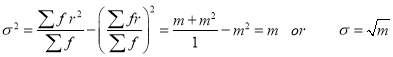
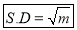
Hence mean and variance of a Poisson distribution are each equal to m. Similarly we can obtain,
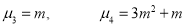
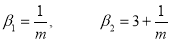
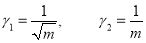
Mean Deviation:
Show that in a Poisson distribution with unit mean, and the mean deviation about the mean is 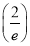 times the standard deviation.
times the standard deviation.
Solution: 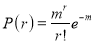 But mean=1 i.e.,
But mean=1 i.e.,  and
and 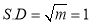
Hence, 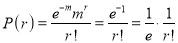
|
|
|
|
0 |
| 1 |
|
1 |
| 0 |
|
2 |
| 1 |
|
3 |
| 2 |
|
4 |
| 4 |
|
… | …. | …. | … |
r |
| r-1 |
|
Mean Derivation
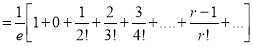

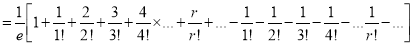
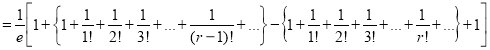
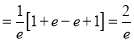
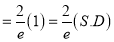
Moment Generating Function of Poisson Distribution

Solution:
Let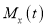 be the moment generating function, then
be the moment generating function, then
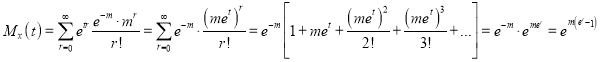
Cumulants
The cumulant generating function 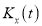 is given by
is given by


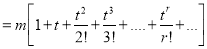
Now  cumulant
cumulant 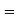 Coefficient of
Coefficient of 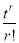 in K(t)
in K(t)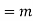
i.e.,  where
where 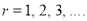
Mean 
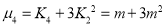

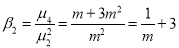
Recurrence formula for Poisson Distribution:
Solution: By Poisson Distribution


On dividing (2) by (1) we get
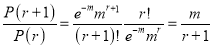

Example
Assume that the probability of on individual coal miner being killed in a mine accident during a year is . Use appropriate statistical distribution to calculate the probability that in a mine employing 200 metres, there will be at least one fatal accident in a year.
. Use appropriate statistical distribution to calculate the probability that in a mine employing 200 metres, there will be at least one fatal accident in a year.
Solution:
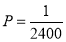 ,
, 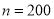
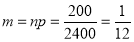
P(At least one)=P(1 or 2 or 3 or …. or 200)
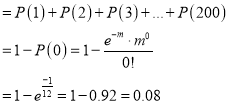
Example:
Suppose 3% of bolts made by a machine are defective, the defects occurring at random during production. If bolts are packaged 50 per box, find
(a) exact probability and
(b) Poisson approximation to it, that a given box will contain 5 defectives.
Solution:
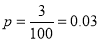
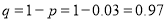
(a) Hence the probability for 5 defective bolts in a lot of 50
 (Binomial Distribution)
(Binomial Distribution)
(b) To get Poisson approximation 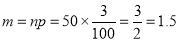
Required Poisson approximation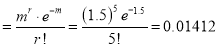
Example:
In a certain factory producing cycle tyres there is a small chance of 1 in 500 tyres to be defective. The tyres are supplied in lots of 10. Using Poisson distribution calculate the approximate number of lots containing no defective, one defective and two defective tyres, respectively, in a consignment of 10000 lots.
Solution:
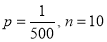
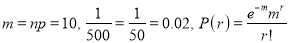
S.No | Probability of defective | Number of lots containing defective |
1 |
|
|
2 |
|
|
3 |
|
|
Normal Distribution:
Normal distribution is a continuous distribution. It is derived a s the limiting form of the Binomial distribution for large values of n and p and q are not very small.
The Normal distribution is given by the equation
 ….(1)
….(1)
Where 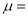 mean,
mean, 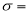 standard deviation,
standard deviation, 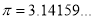 ,
, 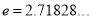
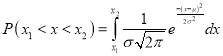
On substitution 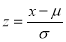 in (1), we get
in (1), we get ….(2)
….(2)
Here mean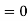 , standard deviation
, standard deviation
(2) is known as standard form of normal distribution.
Mean for Normal Distribution:
Mean [Putting
[Putting 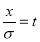 ]
]
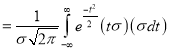
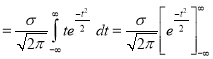
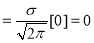
Standard Deviation for Normal Distribution:
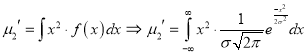
Put 
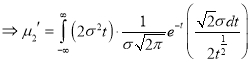

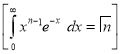



Median of the Normal Distribution
If a is the median, then it divides the total area into two equal halves so that,
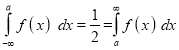
Where 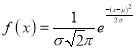
Suppose mean,
mean, 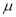 then
then
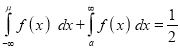 [But
[But ]
]
 (
( mean)
mean)

Thus 
Similarly, when 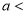 mean, we have
mean, we have
Thus, median=median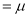 .
.
Mean Deviation about the Mean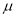
Mean Deviation 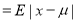
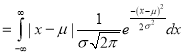
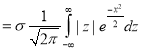 where
where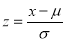
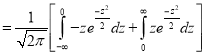
 (as the function is given)
(as the function is given)
 approximately.
approximately.
Mode of the Normal distribution
We know that mode is the value of the variate x for which 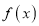 is maximum. Thus, by differential calculus
is maximum. Thus, by differential calculus 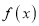 is maximum if
is maximum if  and
and 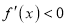
Where 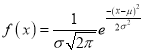
Clearly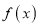 will be maximum when the exponent will bemaximum which will be the when
will be maximum when the exponent will bemaximum which will be the when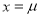
Thus mode is  and modal ordinate
and modal ordinate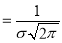
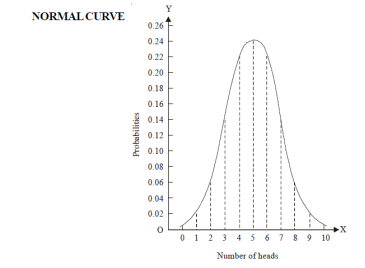
Let us show binomial distribution graphically. The probabilities of heads in 1 tosses are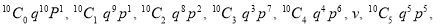
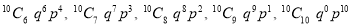 .
.
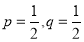 . It is shown in the given figure.
. It is shown in the given figure.
If the variates (heads here) are treated as if they were continuous, the required probability curve will be a normal curve as shown in the above figure by dotted lines.
Properties of the normal curve:
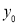
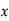
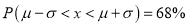
(b) 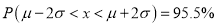
(c) 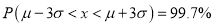
Hence (a) About 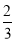 of the values will lie between
of the values will lie between  and
and 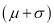 .
.
(b) About 95% of the values will lie between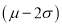 and
and 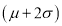 .
.
(c) About 99.7% of the values will lie between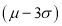 and
and  .
.
Area under the Normal curve
By taking  , the standard normal curve is formed.
, the standard normal curve is formed.
The total area under this curve is 1. The area under the curve is divided into two equal parts by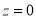 . Left hand side are and right hand side area to
. Left hand side are and right hand side area to  is
is  . The area between the ordinate
. The area between the ordinate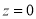 .
.
Example
On final examination in mathematics, the mean was 72, and the standard deviation was 15. Determine the standard deviation scores of students receiving graders.
(a) 60 (b) 93 (c) 72
Solution:
(a)  (b)
(b)  (c)
(c) 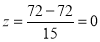
Example: Find the area under the normal curve in each of the cases.

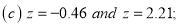



Solution:
(a) Area between  and
and  (b) Area between
(b) Area between  and
and 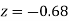
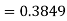

(c) Required area 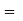 (Area between
(Area between  and
and 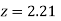 )+
)+
(Area between 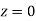 and
and  )
)
=( Area between  and
and 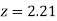 )
)
+( Area between 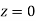 and
and  )
)

(d) Required area  (Area between
(Area between  and
and 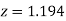 ) – (Area between
) – (Area between  and
and 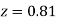 )
)
(e) Required area (Area between
(Area between 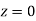 and
and 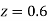 )
)

(f) Required area = (Area between 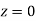 and
and 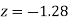 )
)
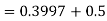
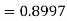
Example. The mean inside diameter of a sample of 200 washers produced by a machine is 0.0502 cm and the standard derivation is 0.005 cm. The purpose for which these washers are intended allows a maximum tolerance in the diameter of 0.496 to 0.508 cm, otherwise the washers are considered defective. Determine the percentage of defective washers produced by the machine, assuming the diameters are normally distributed
Solution:


Area for non-defective washers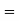 Area between
Area between 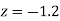 and
and 
= 2 Area between 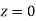 and
and 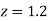
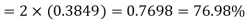
Percentage of defective washers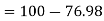
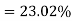
Example:
A manufacturer knows from experience that the resistance of resistors he produces is normal with mean 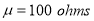 and standard deviation
and standard deviation  What percentage of resistors will have resistance between 98 ohms and 102 ohms?
What percentage of resistors will have resistance between 98 ohms and 102 ohms?
Solution:

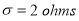

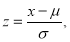
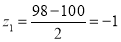
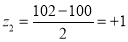
Area between  and
and 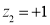
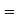 ( Area between
( Area between  and
and 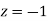 )+( Area between
)+( Area between  and
and  )
)
 ( Area between
( Area between 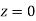 and
and  )=2
)=2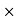 0.3413=0.6826
0.3413=0.6826
Percentage of resistors having resistance between 98 ohms and 102 ohms =68.26
Example
In a normal distribution, 31% of the items are under 45 and 8% are over 64. Find the mean and standard deviation of the distribution.
Solution:
Let 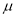 be the mean and
be the mean and 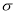 the S.D.
the S.D.
If 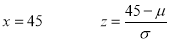
If 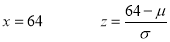
Area between 0 and 
[From the table, for the area 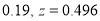 ]
]
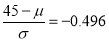 …(1)
…(1)
Area between 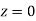 and
and 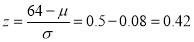
(From the table, for area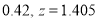 )
)
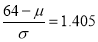 …(2)
…(2)
Solving (1) and (2), we get
Correlation
So far we have confined our attention to the analysis of observation on a single variable. There are , however, many phenomenae where the changes in one variable are related to the changes in the other variable. For instance, the yield of crop varies with the amount of rainfall, the price of a commodity increases with the reduction in its supply and so on. Such a simultaneous variation, i.e., when the changes in one variable are associated or followed by change in the other, is called correlation. Such a data connecting two variables is called bivariate population.
If an increase (or decrease) in the values of one variable corresponds to an increase (or decrease) in the other, the correlation is said to be positive. If the increase (or decrease) in one corresponds to the decrease (or increase) in other, the correlation is said to be negative. If there is no relationship indicated between the variables, they are said to be independent or uncorrelated.
To obtain a measure of relationship between the two variable, we plot their corresponding values on the graph, taking one of the variables along the x-axis and the other along the y-axis (Fig 35.6).
Let the origin be shifted to,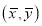 where
where 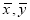 are the means of x’s and y’s that the new co-ordinates are given by
are the means of x’s and y’s that the new co-ordinates are given by
 ,
, 
Now the points (X,Y) are so distributed over the four quadrants of XY –plane that the product XY is positive in the first and third quadrants but negative in the second and fourth quadrants. The algebraic sum of the products can be taken as describing the trend of the dots in all the quadrants.
 (i) If
(i) If is possible the trend of the dots is through the first and third quadrants,
is possible the trend of the dots is through the first and third quadrants,
(ii) If 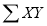 is negative the trend of the dots is in the second and fourth quadrants, and
is negative the trend of the dots is in the second and fourth quadrants, and
(iii) If 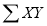 is zero, the points indicate no trend i.e., the points are evenly distributed over the four quadrants.
is zero, the points indicate no trend i.e., the points are evenly distributed over the four quadrants.
The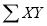 or better still
or better still  , i.e., the average of n products may be taken as a measure of correlation. If we put X and U in their units, i.e., taking
, i.e., the average of n products may be taken as a measure of correlation. If we put X and U in their units, i.e., taking 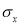 as the unit for
as the unit for  and
and 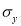 for
for 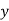 , then
, then
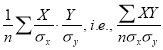
is the measure of correlation.
Coefficient of Correlation:
The numerical measure of correlation is called the coefficient of correlation and is defined by the relation
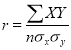
Where 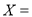 derivation from the mean
derivation from the mean  ,
,
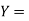 derivation from the mean
derivation from the mean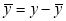
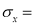 S.D of x – series,
S.D of x – series, 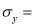 S.D of y-series and
S.D of y-series and
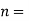 number of values of the two variables.
number of values of the two variables.
Methods of calculation:
(a) Direct method. Substituting the value of 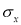 and
and in the above formula, we get
in the above formula, we get 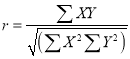
Another form of the formula (1) which is quite handy for calculation is
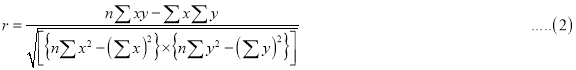
(b) Step deviation method. The direct method become very lengthy and tedious if the means of the two series are not integers. In such cases, use is made of assumed means. If 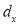 and
and 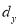 are step-deviation from the assumed means, then
are step-deviation from the assumed means, then
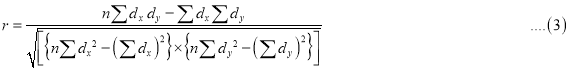
Where  and
and 
Obs: The change of origin and units do not alter the value of the correlation coefficient since r is a pure number.
(c) Co-efficient of correlation for grouped data. When x and y series ae both given as frequency distributions, these can be represented by a two-way table known as the correlation-table. The co-efficient of correlation for such a bivariate frequency distribution is calculated by the formula.
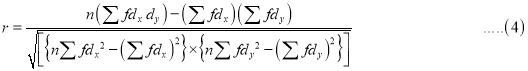
Where  deviation of the central values from the assumed mean of x – series,
deviation of the central values from the assumed mean of x – series,
 deviation of the central values from the assumed mean of y-series,
deviation of the central values from the assumed mean of y-series,
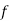 is the frequency corresponding to the pair
is the frequency corresponding to the pair 
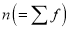 is the total number of frequencies.
is the total number of frequencies.
Example
Psychological tests of intelligence and of engineering ability were applied to 10 students. Here is a record of ungrouped data showing intelligence ratio (I.R) and engineering ratio (E.R). Calculate the co-efficient of correlation.
Student | A | B | C | D | E | F | G | H | I | J |
I.R | 105 | 104 | 102 | 101 | 99 | 98 | 96 | 92 | 93 | 92 |
E.R | 101 | 103 | 100 | 98 | 96 | 104 | 92 | 94 | 97 | 94 |
Solution:
We construct the following table:
Student | Intelligence ratio | Engineering ratio |
|
|
|
A B C D E F G H I J | 100 6 104 5 102 3 101 2 100 1 99 0 98 -1 96 -3 93 -6 92 -7 | 101 3 103 5 100 2 98 0 95 -3 96 -2 104 6 92 -6 97 -1 94 -4 | 36 25 9 4 1 0 1 9 36 49 | 9 25 4 0 9 4 36 36 1 16 | 18 25 6 0 -3 0 -6 18 6 28 |
Total | 990 0 | 980 0 | 170 | 140 | 92 |
From this table, mean of 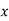 i.e.,
i.e., 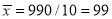 and mean of
and mean of 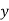 , i.e.,
, i.e., 

Substituting these values in the formula (1), we have
Example:
The correlation table given below shows that the ages of husband and wife of 53 married couples living together on the census night of 1991. Calculus the coefficient of correlation between the age of the husband and that of the wife.
Age of husband | Age of wife | Total | |||||
15 - 25 | 25 – 35 | 35 – 45 | 45 – 55 | 55 – 65 | 65 – 75 | ||
15 – 25 25 - 35 35 - 45 45 – 55 55 – 65 65 - 75 | 1 2 - - - - | 1 12 4 - - - | - 1 10 3 - - | - - 1 6 2 - | - - - 1 4 1 | - - - - 2 2 | 2 15 15 10 8 3 |
Total | 3 | 17 | 14 | 9 | 6 | 4 | 53 |
Solution:
Age of husband | Age of wife | Suppose | |||||||||||
15-25 | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 |
Total | |||||||
Years |
Mid Pt. |
20 |
30 |
40 |
50 |
60 |
70 | ||||||
|
|
|
| -20 | -10 | 0 | 10 | 20 | 30 |
|
|
| |
Age Group | Mid Pt. |
|
| -2 | -1 | 0 | 1 | 2 | 3 | ||||
15-25 | 20 | -20 | -2 |
|
|
|
|
|
| 2 | -4 | 8 | 6 |
25-35 | 30 | -10 | -1 |
|
|
|
|
|
| 15 | -15 | 15 | 16 |
35-45 | 40 | 0 | 0 |
|
|
|
|
|
| 15 | 0 | 0 | 0 |
45-55 | 50 | 10 | 1 |
|
|
|
|
|
| 10 | 10 | 10 | 8 |
55-65 | 60 | 20 | 2 |
|
|
|
|
|
| 8 | 16 | 32 | 32 |
65-75 | 70 | 30 | 3 |
|
|
|
|
|
| 3 | 9 | 27 | 24 |
Total | 3 | 17 | 14 | 9 | 6 | 4 | 53 | 16 | 92 | 86 | |||
| -6 | -17 | 0 | 9 | 12 | 12 | 10 | Thick figures in small squares Stand for | |||||
| 12 | 17 | 0 | 9 | 24 | 36 | 98 | ||||||
| 8 | 14 | 0 | 10 | 24 | 30 | 86 | ||||||
With the help of the above correlation table, we have
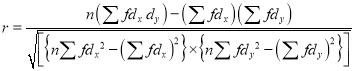
 (approx.)
(approx.)
Line of Regression:
It frequently happens that the dots of the scatter diagram generally, tend to cluster along a well-defined direction which suggests a linear relationship between the variables 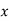 and
and  . Such a line of best-fit for the given distribution of dots is called the line of regression. (Fig 25.6). In fact there are two such lines, one giving the best possible mean values of
. Such a line of best-fit for the given distribution of dots is called the line of regression. (Fig 25.6). In fact there are two such lines, one giving the best possible mean values of 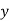 . The former is known as the line of regression of y on x and the latter as the line of regression of x on y.
. The former is known as the line of regression of y on x and the latter as the line of regression of x on y.
Consider first the line of regression of y on x. Let the straight line satisfying the general trend of n dots in a scatter diagram be
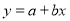 …. (1)
…. (1)
We have to determine the constants a and b so that (1) gives for each value of x, the best estimate for the average value of y in accordance with the principle of least squares therefore, the normal equations for a and b are
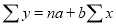 …. (2)
…. (2)
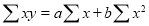 …. (3)
…. (3)
(2) gives 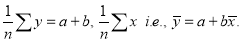
This shows that  , i.e., the means of x and y, lie on (1).
, i.e., the means of x and y, lie on (1).
Shifting the origin to , (3) takes the form
, (3) takes the form
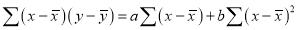 , but
, but  ,
,

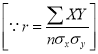
Thus the line of best fit becomes 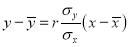 …. (4)
…. (4)
Which is the equation of the line of regression of y on x. Its slope is called the regression coefficient of y on x.
Interchanging x and y, we find that the line of regression of x on y is
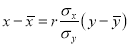 …. (5)
…. (5)
Thus the regression coefficient of y on 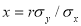 …. (6)
…. (6)
and the regression coefficient of x on 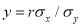 …. (7)
…. (7)
Cor. The correlation coefficient 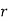 is the geometric mean between the two regression co-efficients.
is the geometric mean between the two regression co-efficients.
For 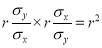
Example
The two regression equations of the variables 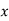 and
and 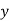 are
are and
and 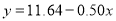 . Find (i) mean of
. Find (i) mean of  ’s (ii) mean of
’s (ii) mean of 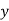 ’s and (iii) the correlation coefficient between
’s and (iii) the correlation coefficient between  and
and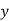 .
.
Solution:
Since the mean of 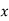 ’s and the mean of
’s and the mean of ’s lie on the two regression line, we have
’s lie on the two regression line, we have

Multiplying (ii) by 0.87 and subtracting from (i), we have


 Regression coefficient of y on x is -0.50 and that of x on y is -0.87.
Regression coefficient of y on x is -0.50 and that of x on y is -0.87.
Now the since coefficient of correlation is the geometric mean between the two regression coefficients.
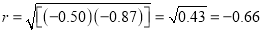
[-ve sign is taken since both the regression coefficients are –ve]
Example.
If  is the angle between the two regression lines, show that
is the angle between the two regression lines, show that
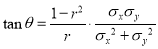
Explain the significance when  and
and  .
.
Solution:
The equations to the line of regression of y on x and x on y are
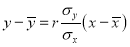 and
and 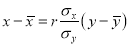
 Their slopes are
Their slopes are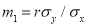 and
and 
Thus 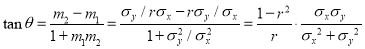
When 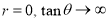 or
or 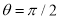 i.e., when the variables are independent, the two lines of regression are perpendicular to each other.
i.e., when the variables are independent, the two lines of regression are perpendicular to each other.
When 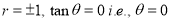 or
or  . Thus the lines of regression coincide i.e, there is perfect correlation between the two variables.
. Thus the lines of regression coincide i.e, there is perfect correlation between the two variables.
Example:
In a partially destroyed laboratory record, only the lines of regression of y on x and x on y are available as  and
and  respectively. Calculate
respectively. Calculate 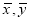 and the coefficient of correlation between x and y.
and the coefficient of correlation between x and y.
Solution:
Since the regression lines pass through , therefore,
, therefore,
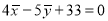 ,
, 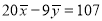
Solving these equations, we get 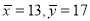
Rewriting the line of regression of y on x as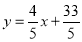 , we get
, we get
 …. (i)
…. (i)
Rewriting the line of regression of x on y as , we get
, we get
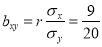 …. (ii)
…. (ii)
Multiplying (i) and (ii), we get
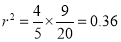
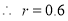
Hence 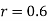 , the positive sign being taken as
, the positive sign being taken as  and
and 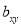 both are positive.
both are positive.
Example:
|
|
8 6 | 12 8 |
While calculating correlation coefficient between two variables x and y from 25 pairs of observations, the following result were obtained: 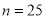 ,
,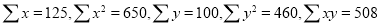 . Later it was discovered at the time of checking that the pairs of values were copied down as
. Later it was discovered at the time of checking that the pairs of values were copied down as
|
|
6 8 | 14 6 |
Obtain the correct value of coefficient.
Solution:
To get the correct results, we subtract the incorrect values and add the corresponding correct values.
The correct results would be

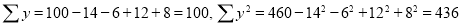
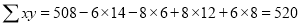
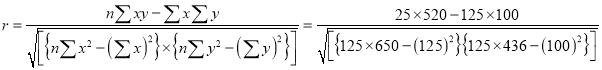
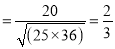
Rank Correlation
A group of n individuals may be arranged in order to merit with respect to some characteristic. The same group would give different orders for different characteristics. Considering the order corresponding to two characteristics A and B for that group of individuals.
Let  be the ranks of the ith individuals in A and B respectively. Assuming that no two individuals are bracketed equal in either case, each of the variables taking the values 1,2,3,…,n, we have
be the ranks of the ith individuals in A and B respectively. Assuming that no two individuals are bracketed equal in either case, each of the variables taking the values 1,2,3,…,n, we have
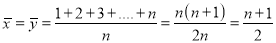
If X,Y be the deviation of x, y from their means, then
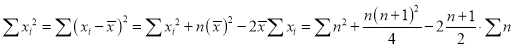
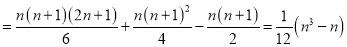
Similarly 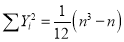
Now let 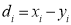 so that
so that 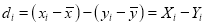
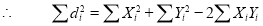

Hence the correlation coefficient between these variables is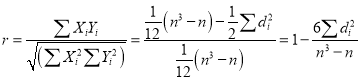
This is called the rank correlation coefficient and is denoted by .
.
Example:
| 1 | 6 | 5 | 10 | 3 | 2 | 4 | 9 | 7 | 8 |
| 6 | 4 | 9 | 8 | 1 | 2 | 3 | 10 | 5 | 7 |
Solution:
If 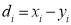 , then
, then 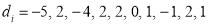

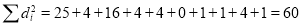
Hence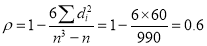 nearly.
nearly.
Example
Three judges A, B, C, give the following ranks. Find which pair of judges has common approach
A | 1 | 6 | 5 | 10 | 3 | 2 | 4 | 9 | 7 | 8 |
B | 3 | 5 | 8 | 4 | 7 | 10 | 2 | 1 | 6 | 9 |
C | 6 | 4 | 9 | 8 | 1 | 2 | 3 | 10 | 5 | 7 |
Solution: Here 
| Ranks by |
|
|
|
|
|
|
|
1 6 5 10 3 2 4 9 7 8 | 3 5 8 4 7 10 2 1 6 9 | 6 4 9 8 1 2 3 10 5 7 | -2 1 -3 6 -4 -8 2 8 1 -1 | -3 1 -1 -4 6 8 -1 -9 1 2 | 5 -2 4 -2 -2 0 -1 1 -2 -1 | 4 1 9 36 16 64 4 64 1 1 | 9 1 1 16 36 64 1 81 1 4 | 25 4 16 4 4 0 1 1 4 1 |
Total |
|
| 0 | 0 | 0 | 200 | 214 | 60 |
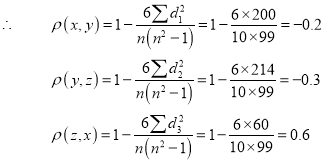
Since  is maximum, the pair of judges A and C have the nearest common approach.
is maximum, the pair of judges A and C have the nearest common approach.
Method of Least Squares:
Let 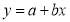 … (1)
… (1)
be the straight line to be fitted to the given data points  .
.
Let  be the theoretical value for
be the theoretical value for  .
.
Then 
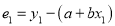
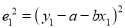


For S to be minimum
 or
or 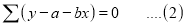
[To generalise  ,
, 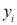 is written as y]
is written as y]
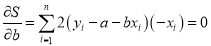 or
or 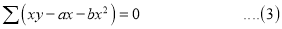
On Simplification equation (2) and (3) becomes


The equations (3) and (4) are known as Normal equations.
On solving equations (3) and (4), we get the values of a and b.
(b) To fit the parabola:

The normal equations are


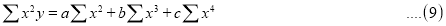
On solving three equations, we get the values of a, b and c.
Note:
1. The normal equation (4) has been obtained by putting on both sides of
on both sides of
equation (1). Equation (5) is obtained by multiplying 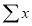 on both sides of (1).
on both sides of (1).
2. The normal equation (7), (8), (9) are obtained by multiply by
 and
and on both sides of equation (6).
on both sides of equation (6).
Example: Find the best values of a and b so that 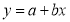 fits the data given in the table.
fits the data given in the table.
X | 0 | 1 | 2 | 3 | 4 |
Y | 1 | 2.9 | 4.8 | 6.7 | 8.6 |
Solution: 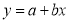
|
|
|
|
0 | 1 | 0 | 0 |
1 | 2.9 | 2.9 | 1 |
2 | 4.8 | 9.6 | 4 |
3 | 6.7 | 20.1 | 9 |
4 | 8.6 | 13.4 | 16 |
| |
|
|
Normal equations 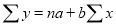 …. (2)
…. (2)
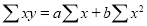 …. (3)
…. (3)
On putting the values of  in (2) and (3), we have
in (2) and (3), we have
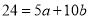 …. (4)
…. (4)
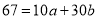 …. (5)
…. (5)
On solving (4) and (5), we get

On Substituting the values of a and b in (1), we get
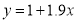
Example: By the method of least squats, find the straight line that best fits the following data:
| 1 | 2 | 3 | 4 | 5 |
| 14 | 27 | 40 | 55 | 68 |
Solution: Let the equation of the straight line best fit be  …. (1)
…. (1)
|
|
|
|
1 | 14 | 14 | 1 |
2 | 27 | 54 | 4 |
3 | 40 | 120 | 9 |
4 | 55 | 220 | 16 |
5 | 68 | 340 | 25 |
|
|
|
|
Normal equations are
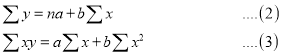
On Putting the values of 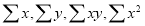 in (2) and (3), we have
in (2) and (3), we have

On solving (4) and (5), we get
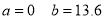
On Substituting the values of a and b in (1), we get

Example: Find the least squares approximation of second degree for the discrete data.
| -2 | -1 | 0 | 1 | 2 |
| 15 | 1 | 1 | 3 | 19 |
Solution:
Let the equation of second-degree polynomial be 
|
|
|
|
|
|
|
-2 | 15 | -30 | 4 | 60 | -8 | 16 |
-1 | 1 | -1 | 1 | 1 | -1 | 1 |
0 | 1 | 0 | 0 | 0 | 0 | 0 |
1 | 3 | 3 | 1 | 3 | 1 | 1 |
2 | 19 | 38 | 4 | 76 | 8 | 16 |
|
|
|
|
|
|
|
Normal equations are
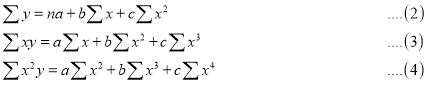
On putting the values of 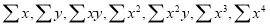 in equations (2), (3), (4), we have
in equations (2), (3), (4), we have
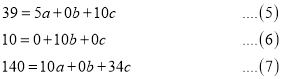
On solving (5), (6), (7), we get 
The required polynomial of second degree is 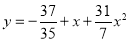
Change of Scale
If the data is of equal interval in large numbers then we change the scale as  .
.
Example: Fit a second degree parabola to the following data by least squares method.
| 1929 | 1930 | 1931 | 1932 | 1933 | 1934 | 1935 | 1936 | 1937 |
| 352 | 356 | 357 | 358 | 360 | 361 | 361 | 360 | 359 |
Solution: Taking 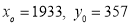
Taking 

The equation 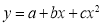 is transformed to
is transformed to 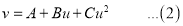
|
|
|
|
|
|
|
|
|
1929 | -4 | 352 | -5 | 20 | 16 | -80 | -64 | 256 |
1930 | -3 | 360 | -1 | 3 | 9 | -9 | -27 | 81 |
1931 | -2 | 357 | 0 | 0 | 4 | 0 | -8 | 16 |
1932 | -1 | 358 | 1 | -1 | 1 | 1 | -1 | 1 |
1933 | 0 | 360 | 3 | 0 | 0 | 0 | 0 | 0 |
1934 | 1 | 361 | 4 | 4 | 1 | 4 | 1 | 1 |
1935 | 2 | 361 | 4 | 8 | 4 | 16 | 8 | 16 |
1936 | 3 | 360 | 3 | 9 | 9 | 27 | 27 | 81 |
1937 | 4 | 359 | 2 | 8 | 16 | 32 | 64 | 256 |
Total |
|
|
|
|
|
|
|
|
Normal equations are

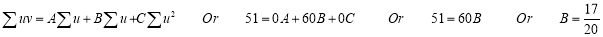

On solving these equations, we get 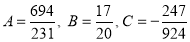
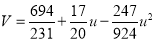
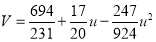
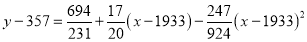
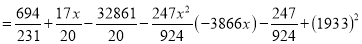


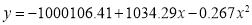
Example: Fit a second-degree parabola to the following data:
x | 0 | 1 | 2 | 3 | 4 |
y | 1 | 1.8 | 1.3 | 2.5 | 6.3 |
Solution: Let 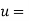 and
and 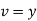 so that the parabola of fit
so that the parabola of fit 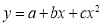 becomes
becomes
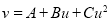 …. (i)
…. (i)
The normal equations are
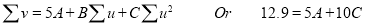
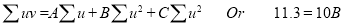

Saving these as simultaneous equations we get

(i) becomes

Or 
Hence 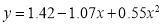
Example: Fit a second degree parabola to the following data:
| 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 1.3 | 1.6 | 2 | 2.7 | 3.4 | 4.1 |
Solution: We shift the origin to (2.5, 0) and take 0.5 as the new unit. This amounts to changing the variable 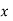 to X, by the relation
to X, by the relation 
Let the parabola of fit be  . The values of
. The values of  etc., ae calculated below:
etc., ae calculated below:
|
|
|
|
|
|
|
|
1.0 | -3 | 1.1 | -3.3 | 9 | 9.9 | -27 | 81 |
1.5 | -2 | 1.3 | -2.6 | 4 | 5.2 | -8 | 16 |
2.0 | -1 | 1.6 | -1.6 | 1 | 1.6 | -1 | 1 |
2.5 | 0 | 2 | 0 | 0 | 0 | 0 | 0 |
3.0 | 1 | 2.7 | 2.7 | 1 | 2.7 | 1 | 1 |
3.5 | 2 | 3.4 | 6.8 | 4 | 13.6 | 8 | 16 |
4.0 | 3 | 4.1 | 12.3 | 9 | 36.9 | 27 | 81 |
Total | 0 | 16.2 | 14.2 | 28 | 69.9 | 0 | 196 |
The normal equations are

Solving these as simultaneous equations, we get

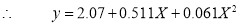
Replacing X by 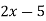 in the above equation, we get
in the above equation, we get
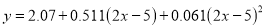
Which simplifies by  . This is the required parabola of best fit.
. This is the required parabola of best fit.
Test of Significance
The tests which enables us to decide whether to accept of to reject the null hypothesis is called the tests of significance. If the difference between the sample values and the population values are so large (lies in critical area). It is to be rejected.
Test of Significance of Large Samples (N>30)
Normal distribution is the limiting case of Binomial distribution when n is large enough. For normal distribution 5% of the items lie outside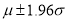 while only 1% of the items lie outside
while only 1% of the items lie outside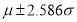 .
.
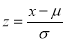
Where z is the standard normal variate and x is the observed number of successes. First we find the value of z. test of significance depends upon the value of z.
(i) (a) If  , difference between the observed and expected number of successes significant at the 5% level of significance.
, difference between the observed and expected number of successes significant at the 5% level of significance.
(b) If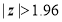 , difference is significant at 5% level of significance.
, difference is significant at 5% level of significance.
(ii) (a) If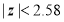 , difference between the observed and expected number of successes significant at 1% level of significance.
, difference between the observed and expected number of successes significant at 1% level of significance.
(b) If 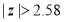 , difference is significant at 1% level of significance.
, difference is significant at 1% level of significance.
Example: A cubical die was thrown 9,000 times and 1 or 6 was obtained 3120 times. Can the deviation from expected value lie due to fluctuations of sampling?
Solution: Let us consider the hypothesis that the die is an unbiased one and hence the probability of obtaining 1 or 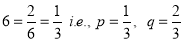
The expected value of the number of successes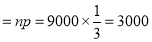
Also 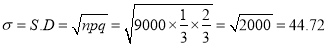

Actual number of successes = 3120
Difference between the actual number of successes and expected number of successes =3120-3000=120 which is <3
Hence the hypothesis is correct and the deviation is due to fluctuations of sampling due random causes.
Example: A coin was tossed 400 times and the head turned up 216 times. Test the hypothesis the coin unbiased at 5% level of significance.
Solution: Suppose the coin is unbiased.
Then the probability of getting the head in a toss 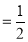
 expected number of successes
expected number of successes 
Thus the excess of observed value over expected value = 216 – 200 = 16
Also S.D. of simple sampling 
Hence 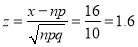
As,  the hypothesis is accepted at 5% level of significance i.e., we conclude that the coin is unbiased at 5% level of significance.
the hypothesis is accepted at 5% level of significance i.e., we conclude that the coin is unbiased at 5% level of significance.
Example: A die was thrown 9000 times and a throw of 5 or 6 was obtained 3240 times. On the assumption of random throwing, do the data indicate an unbiased die?
Solution: Suppose the die is unbiased.
Then the probability of throwing 5 or 6 with one die
The expected number of successes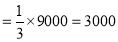
And the observed value of successes = 3240
Thus the excess of observed value over expected value 3240-3000=240
Also S.D. of simple sampling 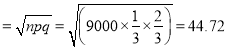
Hence 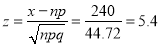 nearly.
nearly.
As  , the hypothesis has to be rejected at1% level of significance and we conclude that the die is biased.
, the hypothesis has to be rejected at1% level of significance and we conclude that the die is biased.
Comparison of Large Samples
Two large samples of sizes 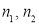 are taken from two populations giving proportions of attributes A’s as
are taken from two populations giving proportions of attributes A’s as 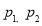 respectively.
respectively.
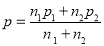
If 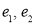 be the standard errors in the two samples then
be the standard errors in the two samples then
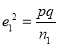 and
and 
If e be the standard error of the differences between 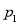 and
and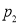 , then
, then
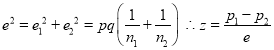
If 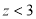 , the difference between
, the difference between 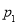 and
and 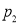 is real one.
is real one.
If  , the difference may be due to fluctuations of simple sampling.
, the difference may be due to fluctuations of simple sampling.
But if z lies between 2 and 3, then the difference is significant at 5% level of significance.
(b) If the proportions of A’s are not the same in the two populations from which the samples are drawn put 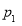 and
and 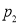 are the true values of proportions then S.E. e of the difference
are the true values of proportions then S.E. e of the difference 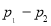 is given by
is given by
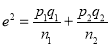
If 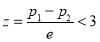 , the difference could have arisen due to fluctuations of simple sampling.
, the difference could have arisen due to fluctuations of simple sampling.
Example: In a city A 20% of a random sample of 900 school boys had a certain slight physical defect. In another city B, 18.5% of random sample of 1600 school boys had the same defect. Is this difference between the proportions significant?
Solutions: We have 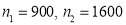
And 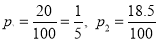
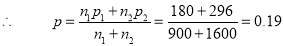
And 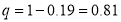
Thus 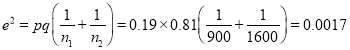
Giving 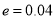 nearly
nearly
Also 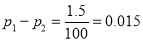

As 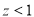 , the difference between the proportions is not significant.
, the difference between the proportions is not significant.
Example: In two large populations there are 30% and 25% respectively of fair haired people. Is this difference likely to be hidden in samples of 1200 and 900 respectively from the two populations?
Solutions:
Here 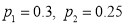 so that
so that 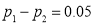 .
.

So that 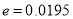
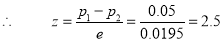
Hence it is unlikely that the real difference will be hidden.
Example: One type of aircraft is found to develop engine trouble in 5 flights out of a total of 100 and another type in 7 flights out of a total of 200 flights. Is there a significant difference in the two types of aircrafts so far as engine defects are concerned?
Solution: 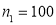 flights, Number of troubled flights
flights, Number of troubled flights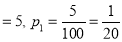
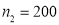 flights, Number of troubled flights
flights, Number of troubled flights

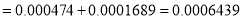
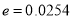
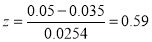
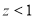 , Difference is not significant.
, Difference is not significant.
Example: In a sample of 600 men from a certain city, 450 are found smokers. In another sample of 900 men from another city, 450 are smokers. Do the data indicate that the cities are significantly different with respect to the habit of smoking among men.
Solution:  men. Number of smokers
men. Number of smokers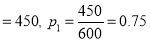
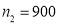 men. Number of smokers
men. Number of smokers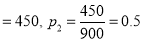

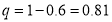

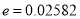

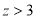 so that the difference is significant.
so that the difference is significant.
Significance Test of a sample mean
Given a random small sample  from a normal population, we have to test the hypothesis that mean of the population is
from a normal population, we have to test the hypothesis that mean of the population is 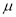 . For this, We first calculate
. For this, We first calculate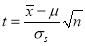 where
where  .
.
Then the find the value of P for the given df from the table.
If the calculated value of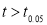 , the difference between
, the difference between  and
and 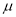 is said to be significant at 5% level if significance.
is said to be significant at 5% level if significance.
If  , the difference is said to be significant at 1% level of significance.
, the difference is said to be significant at 1% level of significance.
If 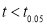 the data is said to be consistent with the hypothesis that
the data is said to be consistent with the hypothesis that 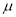 is the mean of population.
is the mean of population.
Example: A certain stimulus administered to each 12 patients resulted in the following increases of blood pressure: 5, 2. 8, -1, 3, 0, 4, 6. Can it be concluded that the stimulus will in general be accompanied by an increase in blood pressure.
Solution:
Let us assume that the stimulus administered to all the 12 patients will increase the B.P. Taking the population to be normal with mean 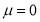 and S.D.
and S.D. ,
,

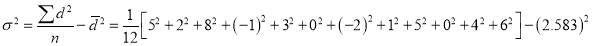
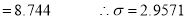
Now 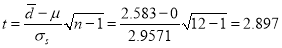
Here 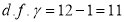
For  , from table IV.
, from table IV.
Since the  , our assumption is rejected i.e., the stimulus does not increase the B.P.
, our assumption is rejected i.e., the stimulus does not increase the B.P.
Example: The nine items of a sample have the following values: 45, 47, 50, 52, 48, 47, 49, 53, 51. Does the mean of these differ significantly from the assumed mean of 47.5?
Solution: We find the mean and standard deviation of the sample as follows:
|
|
|
45 | -3 | 9 |
47 | -1 | 1 |
50 | 2 | 4 |
52 | 2 | 4 |
48 | 0 | 0 |
47 | -1 | 1 |
49 | 1 | 1 |
53 | 5 | 25 |
51 | 3 | 9 |
Total | 10 | 66 |

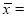 mean
mean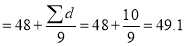



Hence 
Here 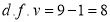
For 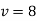 , we get table IV,
, we get table IV, 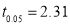
As calculated value of  , the value of t is not significant at 5% level of significance which implies that there is no significant difference between
, the value of t is not significant at 5% level of significance which implies that there is no significant difference between 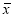 and
and  . Thus the test provides no evidence against that provides no evidence against the population mean being 47.5.
. Thus the test provides no evidence against that provides no evidence against the population mean being 47.5.
Example: A machinist is making engine parts with axle diameter of 0.7 inch. A random sample of 10 parts shows mean diameter 0.742 inch with
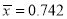
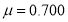

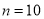
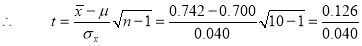
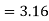
Degree of freedom 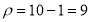
For 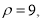 we get from table IV,
we get from table IV, 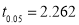 .
.
As the calculated value of 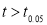 , the value of t is significant at 5% level of significant at 5% level of significance. This implies that
, the value of t is significant at 5% level of significant at 5% level of significance. This implies that 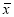 differs significantly from
differs significantly from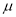 and the hypothesis is rejected. Hence the work is inferior. In fact, the work is inferior even at 2% level of significance.
and the hypothesis is rejected. Hence the work is inferior. In fact, the work is inferior even at 2% level of significance.
Significance Test of difference between sample means:
Given two independent samples 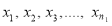 and
and 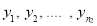 with means
with means 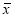 and
and standard deviations
standard deviations  and
and  from a normal population with the same variance, we have to test the hypothesis that the population means
from a normal population with the same variance, we have to test the hypothesis that the population means 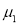 and
and are the same.
are the same.
For this, we calculate  …. (1)
…. (1)
Where 

And 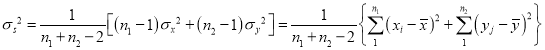
It can be shows that the variate t defined by (1) follows the t – distribution with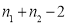 degrees of freedom.
degrees of freedom.
If the calculated value of  the difference between the sample means is said to be significant at 5% level of significance.
the difference between the sample means is said to be significant at 5% level of significance.
If 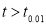 , the difference is said to be significant at 1% level of significance.
, the difference is said to be significant at 1% level of significance.
If  , the data is said to be consistent with the hypothesis, that
, the data is said to be consistent with the hypothesis, that 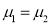 .
.
Cor: If the two samples are of the same size and the data are paired, then t is defined by
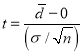 where
where 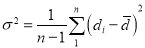
 difference of the ith members of the samples;
difference of the ith members of the samples;
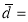 mean of the difference
mean of the difference 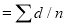 ; and the number
; and the number
Example: Eleven students were given a test in statics. They were given a month’s further tuition and a second test of equal difficulty was held at the end of it. Do the marks give evidence that the students have benefitted by extra coaching?
Boys | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Marks I test | 23 | 20 | 19 | 21 | 18 | 20 | 18 | 17 | 23 | 16 | 19 |
Marks II test | 24 | 19 | 22 | 18 | 20 | 22 | 20 | 20 | 23 | 20 | 17 |
Solution: We compute the means and the S.D. of the difference between the marks of the two tests as under:
 mean of d’s
mean of d’s
Assuming that the students have not been benefited by extra coaching, it implies that the mean of the difference between the marks of the two tests is zero i.e., 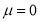 .
.
Then 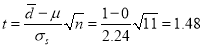 nearly and
nearly and 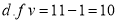
Students |
|
|
|
|
|
1 | 23 | 24 | 1 | 0 | 0 |
2 | 20 | 19 | -1 | -2 | 4 |
3 | 19 | 22 | 3 | 2 | 4 |
4 | 21 | 18 | -3 | -4 | 16 |
5 | 18 | 20 | 2 | 1 | 1 |
6 | 20 | 22 | 2 | 1 | 1 |
7 | 18 | 20 | 2 | 1 | 1 |
8 | 17 | 20 | 3 | 2 | 4 |
9 | 23 | 23 | - | -1 | 1 |
10 | 16 | 20 | 4 | 3 | 9 |
11 | 19 | 17 | -2 | -3 | 9 |
|
|
| |
|
|
From table IV, we find that  (for
(for  )
)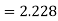 . As the calculated value of
. As the calculated value of 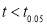 , the value of t is not significant at 5% level of significance i.e., the test provides no evidence that the students have benefited by extra coaching.
, the value of t is not significant at 5% level of significance i.e., the test provides no evidence that the students have benefited by extra coaching.
Example:
From a random sample of 10 pigs fed on diet A, the increases in weight in a certain period were 10, 6, 16, 17, 13, 12,8, 14,15, 9 lbs. for another random sample of 12 pigs fed on diet B, the increases in the same period were 7,13, 22, 15, 12, 14, 18, 8, 21, 23, 10, 17 lbs. test whether diets A and B differ significantly as regards their effect on increases in weight?
Solution: We calculate the means and standard deviations of the sample as follows:
| Diet A |
|
| Diet B |
|
|
|
|
|
|
|
10 | -2 | 4 | 7 | -8 | 64 |
6 | -6 | 36 | 13 | -2 | 4 |
16 | 4 | 16 | 22 | 7 | 49 |
17 | 5 | 25 | 15 | 0 | 0 |
13 | 1 | 1 | 12 | -3 | 9 |
12 | 0 | 0 | 14 | -1 | 1 |
8 | -4 | 16 | 18 | 3 | 9 |
14 | 2 | 4 | 8 | -7 | 49 |
15 | 3 | 9 | 21 | 6 | 36 |
9 | -3 | 9 | 23 | 8 | 64 |
|
|
| 10 | -5 | 25 |
|
|
| 17 | 2 | 4 |
120 | 0 | 120 | 180 | 0 | 314 |

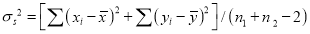
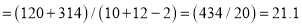

Assuming that the samples that the samples do not differ in weight so far as the two diets are connected i.e.,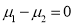
Hence 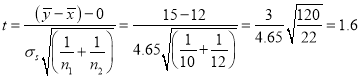 nearly
nearly
Here 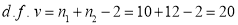
For 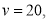 we find
we find 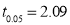 [From table IV]
[From table IV]
 the calculated value of
the calculated value of 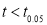 .
.
Hence the difference between the sample means is not significant i.e., the two diets do not differ significantly as regards their effect on increase in weight.
Chi-Square (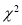 ) Test:
) Test:
When a fair coin is tossed 80 times, we expect from theoretical considerations that heads will appear 40 times. But this never happens in practice i.e., the results obtained in an experiment do not agree exactly with the theoretical results. The magnitude of discrepancy between observation and theory is given by the quantity 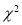 (pronounced as chi-square). If
(pronounced as chi-square). If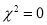 , the observed and theoretical frequencies completely agree. As the value of
, the observed and theoretical frequencies completely agree. As the value of  increases, the discrepancy between the observed and theoretical frequencies increases.
increases, the discrepancy between the observed and theoretical frequencies increases.
Definition: If 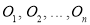 be a set of observed (experimental) frequencies and
be a set of observed (experimental) frequencies and 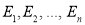 be the corresponding set of expected (theoretical) frequencies, then
be the corresponding set of expected (theoretical) frequencies, then 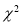 is defined by the relation
is defined by the relation
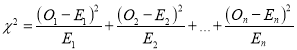

With 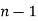 degrees of freedom.
degrees of freedom. 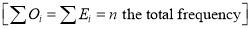
Chi-Square distribution
If 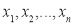 be
be  independent normal variates with mean zero and s.d. unity, then it can be shown that
independent normal variates with mean zero and s.d. unity, then it can be shown that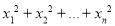 , is a random variate having
, is a random variate having  -distribution with
-distribution with 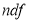 .
.
The equation of the  -curve is
-curve is
 …. (2)
…. (2)
Where 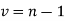 (Fig 27.3)
(Fig 27.3)
Properties of  -distribution
-distribution
(i) If 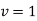 , the
, the  - curve (2) reduces to
- curve (2) reduces to  , which is the exponential distribution.
, which is the exponential distribution.
(ii) If  , this curve is tangential to x-axis at the origin and is positively skewed as the mean is at v and mode at v-2.
, this curve is tangential to x-axis at the origin and is positively skewed as the mean is at v and mode at v-2.
(iii) The probability P that the value of 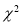 from a random sample will exceed
from a random sample will exceed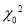 is given by
is given by

The values of 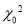 have been tabulated for various values of P and for values of v from 1 to 30. (Table-V Appendix 2)
have been tabulated for various values of P and for values of v from 1 to 30. (Table-V Appendix 2)
For 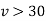 , the
, the 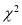 -curve approximate to the normal curve and we should refer to normal distribution tables for significant values of
-curve approximate to the normal curve and we should refer to normal distribution tables for significant values of 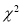 .
.
(iv) Since the equation of 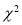 -curve does not involve any parameters of the population, this distribution does not depend on the form of population and is therefore, very useful in a large number of problems.
-curve does not involve any parameters of the population, this distribution does not depend on the form of population and is therefore, very useful in a large number of problems.
(v) Mean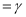 and variance
and variance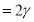
Goodness of Fit
The value of 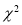 is used to test whether the deviation of the observed frequencies from the expected frequencies are significant or not. It is also used to test how will a set of observations fit a given distribution,
is used to test whether the deviation of the observed frequencies from the expected frequencies are significant or not. It is also used to test how will a set of observations fit a given distribution, therefore, provides a test of goodness of fit and may be used to examine the validity of some hypothesis about an observed frequency distribution. As a test of goodness of fit, it can be used to study the correspondence between theory and fact.
therefore, provides a test of goodness of fit and may be used to examine the validity of some hypothesis about an observed frequency distribution. As a test of goodness of fit, it can be used to study the correspondence between theory and fact.
This is a non-parametric distribution free test since in this we make no assumption about the distribution of the parent population.
Procedure to test significance and goodness of fit.
(i) Set up a ‘null hypothesis’ and calculate
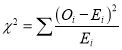
(ii) Find the df and read the corresponding values of 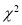 at a prescribed significance level from Table V.
at a prescribed significance level from Table V.
(iii) From 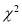 - table, we can also find the probability P corresponding to the calculated values of
- table, we can also find the probability P corresponding to the calculated values of  for the given d.f.
for the given d.f.
(iv) If P<0.05, the observed value of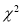 is significant at 5% level of significance.
is significant at 5% level of significance.
(v) If P<0.01, the value is significant at 1% level.
(vi) If P>0.05 it is a good fit and the value is not significant.
Example:
A set of five similar coins is tossed 320 times and the result is
No. of heads | 0 | 1 | 2 | 3 | 4 | 5 |
Frequency | 6 | 27 | 72 | 112 | 71 | 32 |
Test the hypothesis that the data follow a binomial distribution.
Solution: For v=5, we have 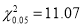
p, probability of getting a head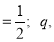 probability of getting a tail
probability of getting a tail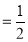
Hence the theoretical frequencies of getting 0, 1, 2, 3, 4, 5 heads are the successive terms of the binomial expansion 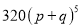
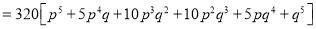

Thus the theoretical frequencies are 10, 50, 100, 100, 50, 10.
Hence
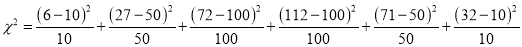
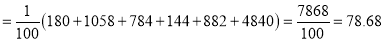
And 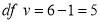
Since the calculated value of 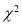 is much greater than
is much greater than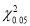 . The hypothesis that the data follow the binomial law is rejected.
. The hypothesis that the data follow the binomial law is rejected.
Example:
Fit a Poisson distribution to the following data and test for its goodness of fit at level of significance 0.05
| 0 | 1 | 2 | 3 | 4 |
| 419 | 352 | 154 | 56 | 19 |
Solution:
Mean 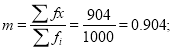

Hence the theoretical frequencies are
| 0 | 1 | 2 | 3 | 4 | Total |
| 404.9 (406.2) | 366 | 165.4 | 49.8 | 11.3 (12.6) | 997.4 |
In order that the total observed and expected frequencies may agree, we take the first and last theoretical frequencies as 406.2 and 12.6 instead of 404.9 and 11.3 as shown in brackets. (In case, the expected frequencies are less than 10, we group together such classes. Here of course, none of the frequencies < 10).

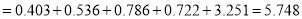
Since the mean of the theoretical distribution has been estimated from the given data and the totals have been made to agree, there are two constraints so that the number of degrees of freedom 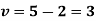 .
.
For  , we have
, we have 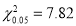 [From table – v]
[From table – v]
Since the calculated value of  , the agreement between the fact and theory is good and hence the poisson distribution can be fitted to the data.
, the agreement between the fact and theory is good and hence the poisson distribution can be fitted to the data.
Example:
In experiments on pea breeding, the following frequencies of sees were obtained:
Round and yellow | Wrinkled and yellow | Round and green | Wrinkled and green | Total |
315 | 101 | 108 | 32 | 556 |
Theory predicts that the frequencies should be in proportions 9:3:3:1. Examine the correspondence between theory and experiment.
Solution:
The corresponding frequencies are
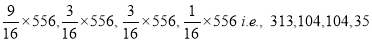
Hence 

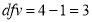
For  , we have
, we have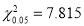
Since the calculated value of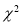 is much less than
is much less than , there is a very high degree of agreement between theory and experiment.
, there is a very high degree of agreement between theory and experiment.
Reference