Unit – 1
Deformation in solids
Below the proportionality limit of the stress-strain curve, the relationship between stress and strain is linear. The slope of this linear portion of the stress-strain curve is the elastic modulus, E, also referred to as the Young's modulus and the modulus of elasticity. Hooke's law expresses the relationship between the elastic modulus, the stress, and the strain in a material within the linear region:
σ = E ε
Where σ is the value of stress and ε is the value of strain.
Hooke's Law in Shear: Hooke's law also has a form relating shear stresses and strains:
τ = G γ
Where τ is the value of shear stress, γ is the value of shear strain, and G is the shear modulus of elasticity. The elastic modulus and the shear modulus are related by:
G = E/2(1+ ν)
Where ν is Poisson's ratio.
The restoring force (F) per unit area (A) is called stress. The unit of stress in S.I system is N/m2 and in C.G.S-dyne/cm2. The dimension of stress = [M1L-1T-2]. Stress is given by,
Stress = F/A
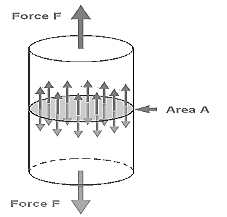
Fig.
Stress could be of the following types:
Strain:
Strain is deformation in the body which we can define as the ratio of change in length to the original length.
ε = ∆L/L
The strain is the relative change in configuration due to the application of deforming forces. It has no unit or dimensions. The strain could be of the following types:
Tensile Stress:
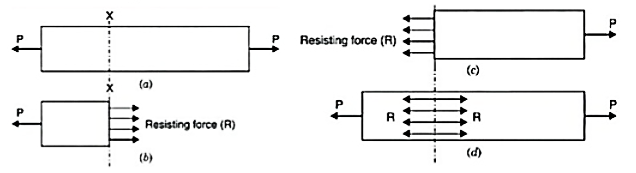
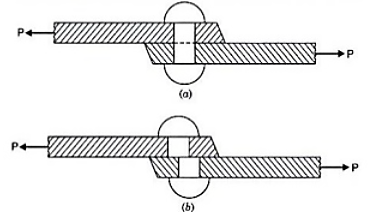
The stress induced in a body, when subjected to two equal and opposite pulls as shown in Fig. 1.2 as a result of which there is an increase in length, is known as tensile stress. The ratio of increase in length to the original length is known as tensile strain. The tensile stress acts normal to the area and it pulls on the area.
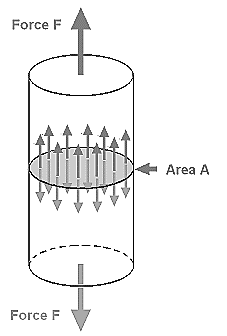
Fig. Tensile stress
Fig. 1.2: Tensile stress Fig. 1.2 (a) shows a bar subjected to a tensile force P at its ends.
Consider a section x-x, which divides the bar into two parts. The part left to the section x-x, will be in equilibrium if P = Resisting force (R). This is shown in Fig. 1.2 (b). Similarly, the part right to the section x-x, will be in equilibrium if P = Resisting force as shown in Fig. 1.2 (c). This resisting force per unit area is known as stress or intensity of stress.
Compressive Stress:
The stress induced in a body, when subjected to two equal and opposite pushes as shown in Fig. 1.3 (a) as a result of which there is a decrease in length of the body, is known as compressive stress. And the ratio of decrease in length to the original length is known as compressive strain. The compressive stress acts normal to the area and it pushes on the area. Let an axial push P is acting on a body in cross-sectional area A. Due to external push P, let the original length L of the body decreases by dL.
The compressive stress is given by-
The compressive strain is given by-
Fig. Compressive stress
Shear Stress:
The stress induced in a body, when subjected to two equal and opposite forces which are acting tangentially across the resisting section as shown in Fig. 1.4 as a result of which the body tends to shear off across the section, is known as shear stress. The corresponding strain is known as shear strain. The shear stress is the stress which acts tangential to the area. It is represented by τ.
Fig. Shear stress
Elastic moduli and the relationship between them
For all isotropic polymeric materials where Hook's law is valid, simple relationships exist between the elastic constants such as Young's modulus E, shear modulus G, bulk modulus B, and Poisson's ratio ν) As long as two of them are known, all others can be predicted. There are many different elastic constants from which we can choose. Often the relation between two moduli is expressed as a function of the Poisson ratio:
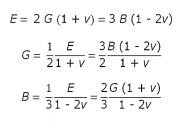
And for the Poisson’s ratio
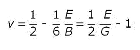
From these relations it follows that −1 < ν < 1/2 are the classical bounds to the Poisson’s ratio. However, almost all classical materials lie within 1/5 < ν < 1/2.1 For isotropic weakly compressible materials such as liquids and rubbers, the Poisson's ratio approaches the upper bound ν = 1/2. In that case the elastic tensile modulus is three time the shear modulus and the bulk modulus is much larger than the Young's modulus,
E ≈ 3 G and B »E
The Poisson's ratio of rubber is never exact 0.5 because this means the elastic bulk modulus would go to infinity which is not possible. However, values very close to 1/2 have been reported (0.4999)1. In the case of quasi-isotropic polycrystalline polymers and other rather stiff isotropic polymers like polystyrene (polymers with bulky side groups), the Poisson's ratio reaches a value of about ν ≈ 1/3.
E ≈ 8/3 G and E ≈ B
For most engineering plastics, ν is in the range 0.35 < ν < 0.45 (see table of Poisson's ratios).
For a (hypothetical) material with no lateral contraction, ν = 0, the elastic tensile modulus is about two times the shear modulus and three times the bulk modulus:
E ≈ 2 G = 3 B
However, most common plastics have much larger Poisson's ratios, ν > 0.3.
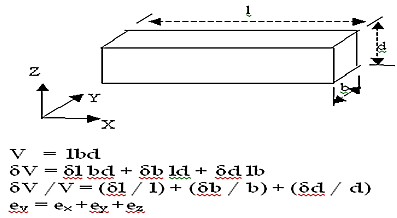
Volumetric strain:
Volumetric strain of a deformed body is defined as the ratio of the change in volume of the body to the deformation to its original volume. If V is the original volume and dV the change in volume occurred due to the deformation, the volumetric strain ev induced is given by-
ev=dV/V
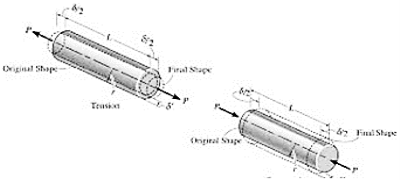
Fig. Consider a uniform rectangular bar of length l, breadth b and depth d as shown in figure. Its volume V is given by,
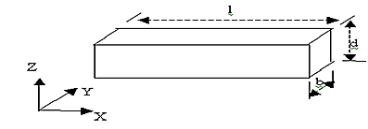
Fig.
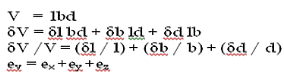
This means that volumetric strain of a deformed body is the sum of the linear strains in three mutually perpendicular directions.
Linear Strain:
It is defined as Linear strain may be either tensile or compressive. If there is some increase in the length of a body due to external force, then the strain is known as tensile strain.
On the other hand, if there is some decrease in the length of the body due to external force, then the strain is known as compressive strain. Please note that both are linear strain only. In the case of rod having uniform cross-section A. the normal stress ζ could be assumed to have a constant value P/A. Thus, it is appropriate to define ε as the ratio of the total deformation δL over the total length L of the rod. Whereas in the case of a member of variable cross-section, however, the normal stress ζ = P/A varies along the member, and it is necessary to define the strain at a given point as
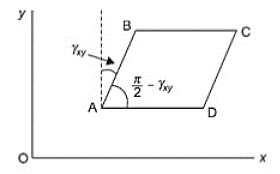
Shear Strain:
It is a measure of the angle through which a body is deformed by the applied force, denoted by γ. The shear strain is represented by the angle through which the other two faces have rotated as shown in Fig.
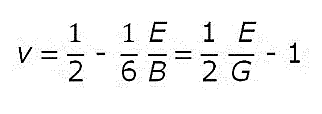
Fig. Shear strain
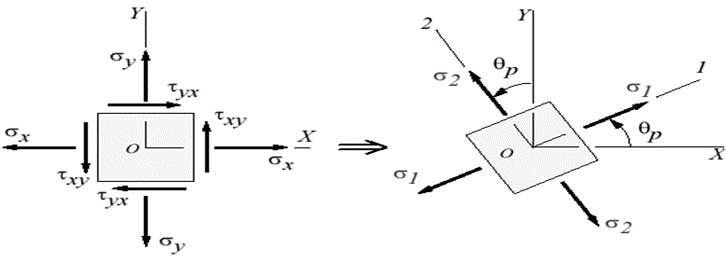
• The magnitude of normal stress and shear stress may vary with respect to the inclination of planes. If we are concerned with the safety of solids under stress, we are required to find on which planes extreme values of normal and shear stress components are present. Hence, it is essential to know:
(a) Maximum tensile stress,
(b) Maximum compressive stress, and
(c) Maximum shear stress.
• The extreme values of normal stresses are called the Principal Stresses and the planes on which the principal stresses act are called the principal planes.
• In two-dimensional problems, there are two principal stresses, namely the major principal stress and the minor principal stress which are defined as the maximum and minimum values of the normal stresses respectively. Here, the maximum or minimum is to be considered algebraically.
• For example, if the principal stresses happen to be 20 N/mm2 tensile and 75 N/mm2 compressive, the tensile stress of 20 N/mm2 is to be taken as the major principal stress denoted by the symbol σ1 and the compressive stress of 75 N/mm2 is to be taken as the minor principal stress (algebraically – 75 N/mm2) and denoted by the symbol σ2. The corresponding planes are defined as major and minor principal planes.
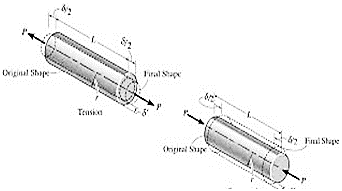
Fig 4: Principal Stress
Expressions of Principal Planes and Principal Stresses:
In calculus, you have learnt that when a function reaches maximum or minimum its derivative with respect to the independent variable becomes zero. Since the normal stress on an arbitrary plane is a function of the aspect angle θ as given by the expression,
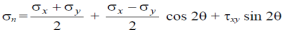
Expression for major and minor principal stresses as follows
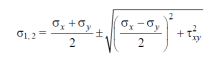
Above equations may be used to readily determine the principal planes and principal stresses.
Geologists and engineers calculate normal and shear stresses from the orientation and magnitude of two of the three principal stresses using the Mohr diagram. This diagram graphically illustrates in two dimensions the complex mathematical relationships between the components that make up a traction Software for graphing the Mohr diagram is provided in Visualizing Stress. However, before using the software to analyse various states of stress, the components that make up the Mohr circle must be first explored
The fundamental stress equations derived in the previous section (Equations and) can be rearranged as follows. For normal stress (sn)
And for shear stress (t)
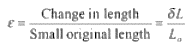
Squaring both sides of Equations and reveals
……….1
And
………………………….2
Combining Equations (1) and (2) yields
Simplifying
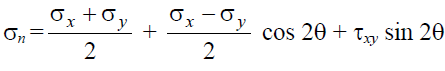
Now recall the trigonometric relationship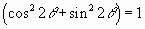 
. Substituting this relationship into the right-hand side of equation results in
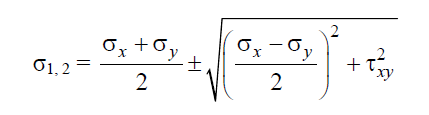
Recall from your college algebra class that the equation of a circle drawn in an x-y coordinate system is
where r is the radius of the circle and (h, k) are the coordinates of the center of the circle. Comparing Equations and reveal that the fundamental stress equations define a circle in sn-t space centered on the point
with a radius of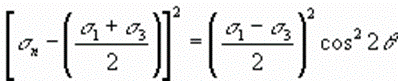 
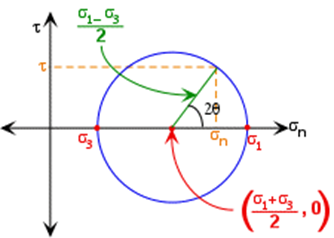
Figure 1 illustrates a circle constructed from Equation.
The circle represents the locus of all possible normal and shear stresses for a given state of stress acting on planes who’s normal make an angle of q degrees to s1.
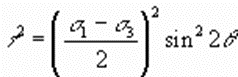
Figure 5 The Mohr circle constructed from Equation with a radius defined by Equation and a center with the coordinates in Equation.
Note further that the average stress is simply
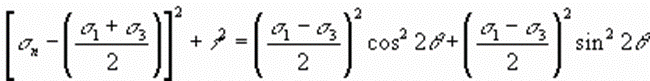
Or, in three dimensions
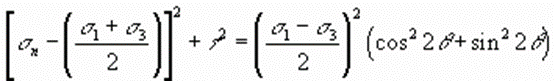
In a Mohr diagram, average stress is the center of the Mohr circle. Differential stress is the difference between the maximum and minimum principal stresses. In a two-dimensional Mohr diagram differential stress is the diameter of the Mohr circle.
Several theories are available however, only four important theories are discussed here:
Maximum shear stress (Tresca) theory for ductile materials
The French engineer Tresca proposed this theory. It states that a member subjected to any state of stress fails (yields) when the maximum shearing stress (τmax)in the member becomes equal to the yield point stress (τy)in a simple tension or compression test (Uniaxial test). Since the maximum shear stress in a material under uniaxial stress condition is one half the value of normal stress and the maximum normal stress (maximum principal stress) is σmax.
Then from Mohr’s circle,
->(1)
Maximum Principal Stress theory or (Rankine Theory):
According to this theory, it is assumed that when a member is subjected to any state of stress, fails (fracture of brittle material or yielding of ductile material) when the principal stress of largest magnitude. (σ1) in the member reaches to a limiting value that is equal to the ultimate stress).
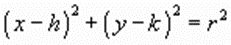
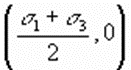
Maximum Normal Strain or Saint Venant’s Criterion:
In this theory, it is assumed that a member subjected to any state of stress fails (yields) when the maximum normal strain at any point equals, the yield point strain obtained from a simple tension or compression test (εy = σy/E). Principal strain of largest magnitude |ε max| could be one of two principal strain ε1 and ε2 depending upon the stress conditions acting in the member.
Thus, the maximum Principal strain theory may be represented by the following equation.
As stress in one direction produces the lateral deformation in the other two perpendicular directions and using law of superposition, we find two principal strains of the element.
Maximum Shear Strain Energy (Distortion Energy Criterion (Von MISES Criterion):
According to this theory when a member is subjected to any state of stress fails (yields) when the distortion energy per unit volume at a point becomes equal to the strain energy of distortion per unit volume at failure (yielding). The distortion strain energy is that energy associated with a change in the shape of the body. The total strain energy per unit volume also called strain energy density is the energy in a body stored internally throughout its volume due to deformation produced by external loading.
Distortion energy per unit volume is given by-
Strain energy due to distortion per unit volume for dual stress system-
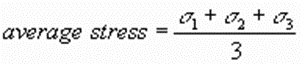
According to distortion energy theory-
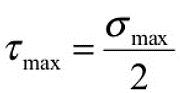
So, equation becomes,
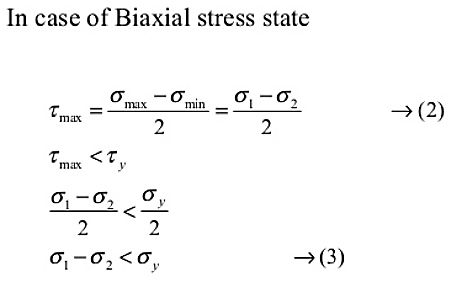
Strain Energy Theory
Failure at any point in a body is defined when the energy density in the body at the applied load equals the energy density corresponds to the elastic limit of the material.
Uni-axial loading:
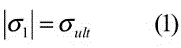
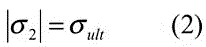
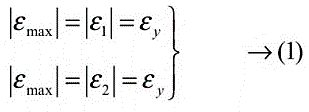
Key takeaway points:
References
