Unit - 1

Force Analysis of Mechanism

1.1 Introduction:

Equilibrium: A rigid body is said to be in equilibrium if it continues it continues its state of motion

The conditions of equilibrium can be written mathematically as:

∑M=0

∑F=0

Static force Analysis

The analysis is carried out by determining all the forces and couples acting on all the pairs. In this analysis, we ignore the forces due to acceleration. Only the effects of external forces applied to the mechanism are considered.

Necessary conditions for static equilibrium of a body for a planar system:

A body is said to be in static equilibrium if it remains in its state of rest or motion. The necessary conditions of static equilibrium are as follows:

(i)                The vector sum of all the forces on body must be zero, that is ∑F=0.

(ii)              The vector sum of all the moment about any arbitrary point must be zero, that is, ∑M=0.

If the body is planar or of 2-Dimensional system, motion then the conditions of static of static equilibrium are as follows:

(i)                ∑Fx=0, that is, sum of all the horizontal components must be zero.

(ii)              ∑Fy=0, that is, sum of all the vertical components must be zero.

(iii)           ∑M=0, that is, sum of all the moment about any arbitrary point must be zero.

Key takeaway point:

(i)                The vector sum of all the forces on body must be zero, that is ∑F=0.

(ii)              The vector sum of all the moment about any arbitrary point must be zero, that is, ∑M=0. For a body to be in a static equilibrium.

1.2 Dynamics of Plane motion of a rigid body:

A rigid body is an idealization of a body that does not deform or change shape. Formally it is defined as a collection of particles with the property that the distance between particles remains unchanged during the course of motions of the body. Like the approximation of a rigid body as a particle, this is never strictly true. All bodies deform as they move. However, the approximation remains acceptable as long as the deformations are negligible relative to the overall motion of the body.

A rigid body executes plane motion when all parts of the body move in parallel planes. It follows that all particles in a rigid body moves in a circular paths about the axis of rotation, and all lines in the body in which are perpendicular to the axis of rotation rotate through the same angle in the same time.

We can use Newton’s equations for particles to derive equations of motion of a rigid body. A rigid body which is constrained to move in a plane, has three degrees of freedom, and hence it has three independent equations of motion which relates the forces in the plane to accelerations.

1.3 Dynamically equivalent two mass system:

In order to determine the motion of a rigid body, under the action of external forces, it is usually convenient to replace the rigid body by two masses placed at a fixed distance apart, in such a way that,

When these three conditions are satisfied, then it is said to be an equivalent dynamical system. Consider a rigid body, having its centre of gravity at G, as shown in Fig.

Let m = Mass of the body,

kG = Radius of gyration about its centre of gravity G,

m1 and m 2 = Two masses which form a dynamical equivalent system, l1 = Distance of mass m1 from G,

l2 = Distance of mass m2 from G,

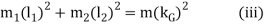
From equations (i)

Substitute the value of and in the equation (iii), we have

This equation gives the essential condition of placing the two masses, so that the system becomes dynamical equivalent. The distance of one of the masses (i.e. either l1 or l2) is arbitrary chosen and the other distance is obtained from equation (vi).

We have discussed the conditions for equivalent dynamical system of two bodies. A little consideration will show that when two masses are placed arbitrarily*, then the conditions (i) and (ii) as given in Art. 15.11 will only be satisfied. But the condition (iii) is not possible to satisfy. This means that the mass moment of inertia of these two masses placed arbitrarily, will differ than that of mass moment of inertia of the rigid body.

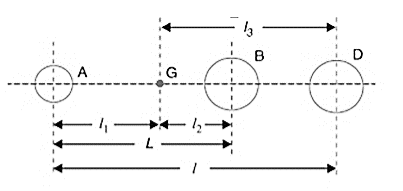
Figure 1: Correction couple to be applied to make the two-mass system dynamically equivalent

Consider two masses, one at A and the other at D be placed arbitrarily, as shown in Fig. 1. Let l3 = Distance of mass placed at D from G,

l1= New mass moment of inertia of the two masses;

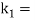New radius of gyration;

Angular acceleration of the body;

Mass moment of inertia of dynamically equivalent system;

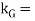Radius of gyration of a dynamically equivalent system. We know that the torque required to accelerate the body

Similarly, the torque required to accelerate the two-mass system placed arbitrarily,

∴ Difference between the torques required to accelerate the two-mass system and the torque required to accelerate the rigid body.

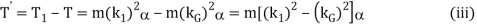
The difference of the torques T' is known as correction couple. This couple must be applied, when the masses are placed arbitrarily to make the system dynamical equivalent. This, of course, will satisfy the condition (iii)

1.4 Correction Torque:

Consider two masses, one at A and the other at D be placed arbitrarily, as shown in Fig

15.21. Let l3  = Distance of mass placed at D from G,

l1= New mass moment of inertia of the two masses;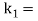 New radius of gyration;

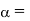Angular acceleration of the body;

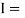Mass moment of inertia of dynamically equivalent system;

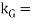Radius of gyration of a dynamically equivalent system. We know that the torque required to accelerate the body

Similarly, the torque required to accelerate the two-mass system placed arbitrarily,

∴ Difference between the torques required to accelerate the two-mass system and the torque required to accelerate the rigid body.

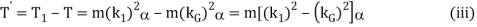
The difference of the torques T' is known as correction Torque. This couple must be applied, when the masses are placed arbitrarily to make the system dynamical equivalent. This, of course, will satisfy the condition (iii)

1.5 Forced in mechanism and machines:

According to the definition, both forces and motions are transmitted and modified in a machine. The way in which the parts of a machine are interconnected and guided to produce a required output motion from a given input motion is known as the mechanism of the machine. The piston, connecting rod, and crankshaft in a reciprocating engine constitute a mechanism for changing the rectilinear motion of the piston into the rotary motion of the crankshaft.

Although both forces and motions are involved in the operation of machines, the primary function of a machine may be either the amplification of force or the modification of motion. A lever is essentially a force increase, while a gearbox is most often used as a speed reducer. The motions and forces in a machine are inseparable, however, and are always in an inverse ratio. The output force on a lever is greater than the input force, but the output motion is less than the input motion. Similarly, the output speed of a gear reducer is less than the input speed, but the output torque is greater than the input torque. In the first case again in force is accompanied by a loss in motion, while in the second case a loss in motion is accompanied by a gain in torque.

Although the primary function of some machines can be identified, it would be difficult to classify all machines as either force or motion modifiers; some machines belong in both categories. All machines, however, must perform a motion-modifying function, since if the parts of a mechanical device do not move; it is a structure, not a machine.

While all machines have a mechanism, and consequently perform a motion-modifying function, some machines do not have a planned force-modifying purpose; the forces that exist are caused by friction and the inertia of the moving masses and do not appear as a useful output effort. This group would include measuring instruments and clocks.

In the science of mechanics, “work” is something that forces do when they move in the direction, in which they are acting, and it is equal to the product of the average force and the distance moved. If a man carries a weight along a horizontal path, he does not work according to this definition, since the force and the motion are at right angles to one another; that is, the force is vertical and the motion horizontal. If he carries the weight up a flight of stairs or a ladder, he does work, since he is moving in the same direction in which he is applying a force.

Key Takeaways:

Mathematically, if F equals force (in Newton) and S equals distance (in feet or metres), work is then equal to the applied force F multiplied by the distance this force moves S, or WORK = F × S.

References:

1. Dr. V. P. Singh, Theory of Machine, Dhanpatrai, and sons.
2. C. S. Sharma & Kamlesh Purohit, “Theory of Machine and Mechanism”, PHI.
3. Sadhu Singh, Theory of Machines, Pearson
4. Google and Power point presentations.