Unit – 3

Cams

3.1 Cams

A cam is a rotating machine element which gives reciprocating or oscillating motion to another element known as follower.

Types of Cams:

Cams can be classified according to:

• Shape
• Follower movement
• Manner of constraint of the follower

3.2 Classification of cams and followers:

3.2.1 Classification of Cam

Though the cams may be classified in many ways, among them we can classified:

1. Radial or disc cam.

2. Cylindrical cam

1. Radial or disc cam: In radial cams, the follower reciprocates or oscillates in a direction perpendicular to the cam axis. The cams as shown in Fig.3.1. Are all radial cams.

Example:  Radial or disc cam.

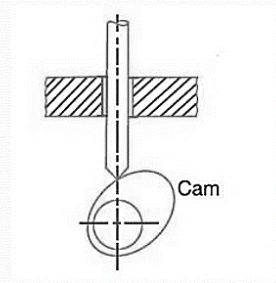
Fig.3.1. Radial or disc cam

2. Cylindrical cam:

In cylindrical cams, the follower reciprocates or oscillates in a direction parallel to the cam axis. The follower rides in a groove at its cylindrical surface. A cylindrical grooved cam with a reciprocating and an oscillating follower is shown in Fig.3.2.

Example: Cylindrical cam.

Fig.3.2. Cylindrical cam

3.2.2 Classification of cams-followers:

1. Knife edge follower: When the contacting end of the follower has a sharp knife edge, it is called a knife edge follower, as shown in Fig.3.3.

Example: Cam with knife edge follower.

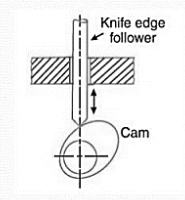
Fig.3.3. Cam with knife edge follower.

2. Roller follower: When the contacting end of the follower is a roller, it is called a roller follower, as shown in Fig.3.4.

Example: Cam with Roller follower.

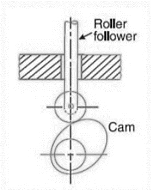
Fig.3.4. Cam with Roller follower

3. Flat faced follower: When the contacting end of the follower is perfectly Flat faced, it is called a Flat faced follower, as shown in Fig.3.5.

Example: Cam with Flat faced follower.

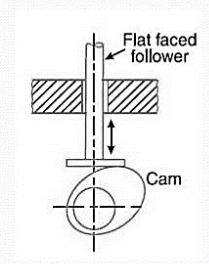
Fig.3.5. Cam with Flat faced follower

4. Spherical faced follower: When the contacting end of the follower is of spherical shape, it is called a spherical faced follower, as shown in Fig.3.6.

Example: Cam with Spherical faced follower.

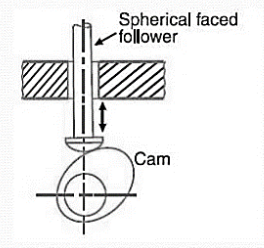
Fig.3.6. Cam with Spherical faced follower.

5. Off-set follower: When the motion of the follower is along an axis away from the axis of the cam center, it is called off-set follower.

Example: Cam with off-set follower.

Fig.3.7. Cam with off-set follower

Key takeaways:

1. Globoidal cam:  In globoidal cams have convex or concave type surface cut on circumference of cam which impart motion to the follower to oscillate about the fulcrum.

Nomenclature of cams:

• Cam Profile: The contour of the working surface of the cam.

• Trace Point: The point at the knife edge of a follower, or the center of a roller, or the center of a spherical face.

• Pitch Curve: The path of the tracer point.

• Base Circle: The smallest circle drawn, tangential to the cam profile, with its center on the axis of the cam shaft. The size of the base circle determines the size of the cam.

• Prime Circle: The smallest circle which can be drawn from the center of the cam and tangent to the pitch curve.

• Prime circle radius: Prime circle radius is the sum of Base circle radius along with radius of roller for roller follower.

• Pressure Angle: The angle between the normal to the pitch curve and the direction of Motion of the follower at the point of contact.

• Lift of stroke: It is the maximum travel of the follower from its lowest position to the topmost position. The maximum rise is called lift.

• Pitch Point: It is a point on the curve having maximum pressure angle.

• Pitch Circle: It is the circle drawn from the center of the cam through the pitch points.

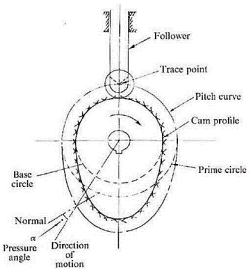
Fig.3.8. Nomenclature of cam profile

3.3 Types of follower and retardation:

Cam followers can be classified according to:

• Shape
• Movement and
• Location of line of movement

3.3.1 Classifications of followers according to shape-

• Knife edge follower
• Roller follower
• Mushroom (or Spherical) follower
• Plate type follower

3.3.2 Classifications of followers according to movement:

1. Reciprocating follower-

In this type, as the cam rotates, the follower reciprocates or translates in the guides.

2. Oscillating follower-

The follower is pivoted at a suitable point on the frame and oscillates as the cam makes rotary motion.

3.3.3 Classifications of followers according to line of movement:

1. Radial follower-

The follower is known as a radial follower if the line of movement of the follower passes through the center of rotation of cam.

2. Offset follower-

If the line of movement of follower is offset from the center of rotation of the cam, the follower is known as an offset follower.

Key takeaway:

Cam followers can be classified according to:

• Shape
• Movement and
• Location of line of movement

3.4 Cam Profile and generation of concentric and offset radial cam profile by graphical method:

The cam motion or profile:

The motion of the cam follower depends upon the profile or shape of the cam. Therefore, the profile determines the resultant action. Cams are expensive to make and therefore the cam follower is normally sacrificial - allowed to wear.

There are three types of cam profile:

•Uniform Velocity

•Uniform acceleration and retardation

•Simple Harmonic Motion

3.4.1 Cam with radial roller follower Cam Profile:

• The cam profile shown in Fig.3.9. May be drawn as explained below:

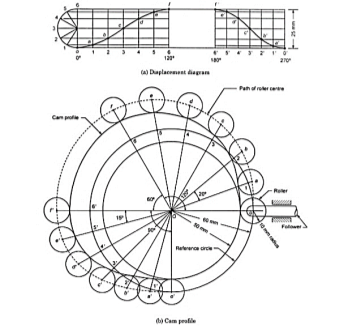
Fig.3.9. Cam profile with radial roller follower

• Draw the base circle with center O and radius 50 mm.
• Draw the reference circle with radius equal to the sum of the radius of base circle and roller radius, i.e., 60 mm. Draw angles of ascent, dwell, and descent of 120°, 60°, and 90°, respectively.
• Divide the angle of ascent and descent into six equal parts.
• Draw radial lines intersecting the reference circle at point 0 to 6 in the angle of ascent and 6′ to 0′ in the angle of descent.
• Measure distances 1a, 2b, etc. from the displacement diagram and mark corresponding distances on the radial lines in the cam profile from the reference circle.
• Repeat the same process in the angle of descent.
• Draw circles at points 0 to f and f′ to 0′ with radius equal to the roller radius of 10 mm. Draw a smooth curve touching (asymptotic) the roller radii to obtain the cam profile.
• Fig. Cam profile with radial roller follower having SHM

3.4.2 Offset Roller Follower:

A cam profile with offset roller follower is shown in Fig.3.10.

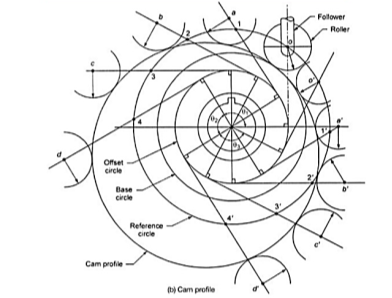
Fig.3.10. Offset radial cam profile

The following steps may be used to draw the cam profile:

• Draw the base circle.
• Draw the follower in its 0° position, tangent to the base circle.
• Draw the reference circle through the centre of the follower in its 0° position.
• Draw the offset circle tangent to the follower centre line.
• Divide the offset circle into a number of divisions corresponding to the divisions in the displacement diagram.
• Draw tangents to the offset circle at each number.
• Lay off various displacements a, b, c, …, etc. along the appropriate tangent lines, measuring from the reference circle.
• Draw in the follower outlines on the various tangent lines.
• Draw a smooth curve to these follower outlines.

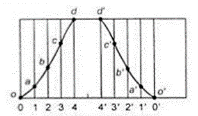
Fig.3.11. Displacement diagram

Key takeaway:

1. Period of dwell: It is the period during which the follower remains stationary for some finite rotation of cam.
2. Lift or stroke: The maximum travel of follower from the lowest position to the highest position is called lift or stroke of the follower.

3.5 Cam with specified contour tangent cam with roller follower, Circular arc cam with flat follower

When the follower moves with the specified motion, the shape of the cam profile thus obtained is difficult and costly to manufacture.

• So, cams with specified contours are specified and motion of follower is determined.

• Cam profiles consisting of circular arcs and straight lines are preferred.

3.5.1 Tangent Cam with reciprocating roller follower tangent cam:

• Flanks of the cam are straight and tangential to the base circle and nose circle.

• Used for operating inlet and exhaust valve of IC Engines.

Tangent cam with reciprocating roller follower tangent cam:

Two cases for derivation of displacement, velocity and acceleration expressions:

1. When the roller has contact with the straight flanks

2. When the roller has contact with the nose.

Let,

Radius of the base circle or minimum radius of the cam,

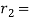Radius of the roller,

Radius of nose,

 = Semi-angle of action of cam or angle of ascent,

Θ = Angle turned by the cam from the beginning of the roller displacement

Φ = Angle turned by the cam for contact of roller with the straight flank, and

ω = Angular velocity of the cam.

CASE 1: When the roller has contact with straight flank displacement:

Let the cam has turned through an angle* θ (less than ϕ) for the roller to have contact at any point (say F) between the straight flanks EG. The centre of roller at this stage lies at C. Therefore displacement (or lift or stroke) of the roller from its lowest position is given by

Displacement

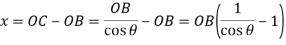
Fig.3.12. When the roller has contact with straight flank displacement

Velocity is given by: -

Differentiating equation (i) with respect to t, we have velocity of the follower,

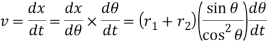
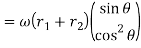
Velocity is maximum where θ maximum

This happens when roller just leaves the contact with the straight flank at G i.e. when .

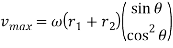
Acceleration is given by: -

Now differentiating equation with respect to t, we have acceleration of the follower,

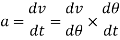
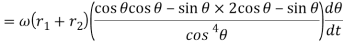
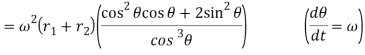
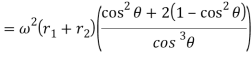
Therefore;

When θ=0° i.e. when the roller is at the beginning of its lift along the straight flank (or when the roller has contact with the straight flank at E).

∴ Minimum acceleration of the follower,

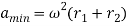
The acceleration is maximum when θ=ϕ i.e. when the roller just leaves contact with the straight flank merges into a circular nose.

∴ Maximum acceleration of the follower,

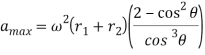
CASE 2: When the roller has contact with the nose displacement:

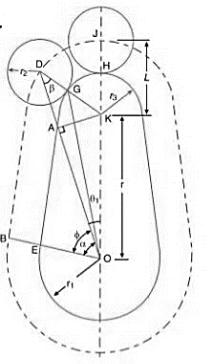
Fig.3.13. Roller has contact with nose displacement

The displacement of the roller is given by

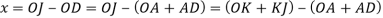
Substituting and we have

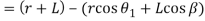
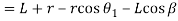
Now from right angles triangles OAK and DAK,

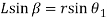
Squaring both sides,

∴

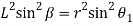
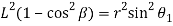
Substituting the value of in equation we get

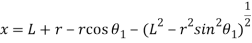
Velocity: -

Differentiating equation with respect to t, we have velocity of the follower,

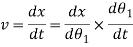
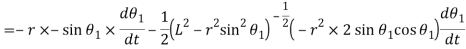
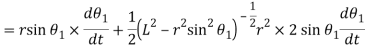
Acceleration: -

Now differentiating equation with respect to t, we have acceleration of the follower,

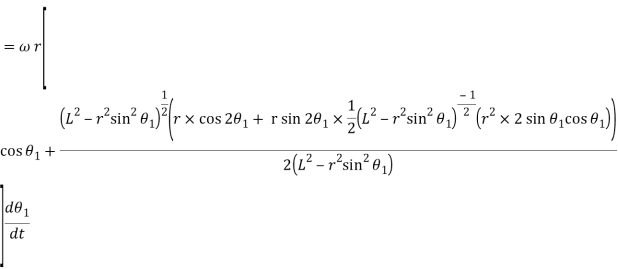
Substituting 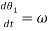and multiplying the numerator and denominator of second term by 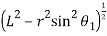, we have

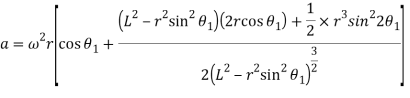
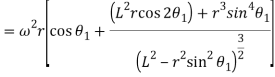
Key takeaway point:

1. When the roller has contact with straight flank displacement then

Velocity is given as:

Acceleration is given by:

2.     When the roller has contact with the nose displacement:

Velocity is given by:

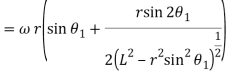
Acceleration is given by:

3.6 Circular arc cam with flat faced follower:

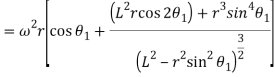
3.6.1 Determining the displacement, velocity and acceleration of the follower when flat face of the follower has contact on the circular flank-

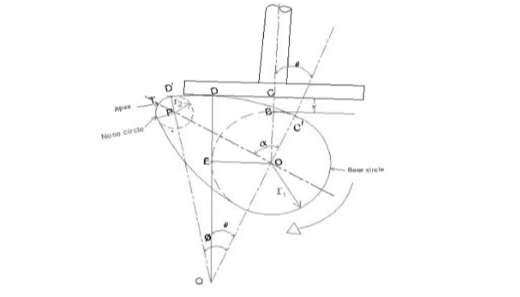
Fig.3.14. Circular arc cam with flat faced follower

Let

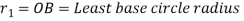
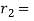Nose circle radius

Flank circle radius

Distance between centre of radius and nose circles.

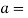Angle of ascent

Φ= Angle of contact on circular flank

Displacement :

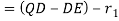
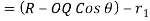
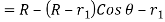
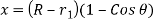
Velocity-

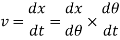
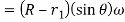
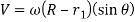
From this equation, it is evident that, at the beginning of the ascent, the velocity is zero (when θ=0) and it increases with θ. It will be maximum when the follower is just shift from circular flank to circular nose.

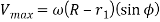
Acceleration-

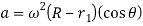
It is obvious from the above equation that at the beginning of the ascent when θ=0, acceleration is maximum and it goes on decreasing and is maximum when θ=ϕ

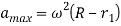
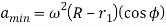
3.6.2 Determining the displacement, velocity and acceleration of the follower when flat face of the follower has contact on the nose-

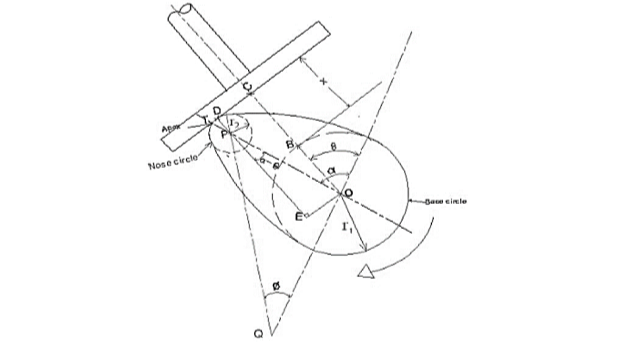
Fig.3.15. Circular arc cam with flat faced of the follower has contact on the nose

Let

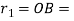Least base circle radius

Nose circle radius

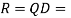Flank circle radius

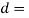Distance between centres of cam and nose circles

Angle of ascent

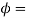Angle of contact on circular flank

Displacement

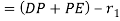
Velocity-

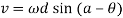
The velocity is minimum when This happens when follower is at the apex of circular nose and it is maximum when 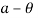is maximum and it is so when the contact changes from circular flank to circular nose i.e.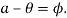

Acceleration-

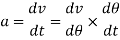
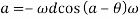
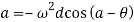
Negative sign indicates retardation. It is maximum when 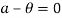i.e., when the follower is at the apex of the nose and minimum 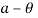is maximum i.e., when the follower changes contact from circular flank to circular nose.

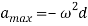
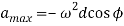
It may be noted that as the contact between cam and follower passes through point D, the acceleration of the follower suddenly changes from 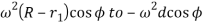i.e., sudden change from positive acceleration to negative acceleration (retardation).

Key takeaway:

1. Determining the displacement, velocity and acceleration of the follower when flat face of the follower has contact on the circular flank.

Velocity is given as-

Acceleration is given as-

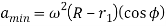
2.     Determining the displacement, velocity and acceleration of the follower when flat face of the follower has contact on the nose.

Velocity is given as-

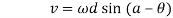
Acceleration is given as-

References:

1. Dr. V. P. Singh, Theory of Machine, Dhanpatrai, and sons.
2. C. S. Sharma & Kamlesh Purohit, “Theory of Machine and Mechanism”, PHI.
3. Sadhu Singh, Theory of Machines, Pearson
4. Various Sites and PPTs. From Google.