Unit - 2

Heat convection

2.1 Heat convection and basic equation

The process of heat transfer between a solid surface and fluid in motion is called convection.

2.1.1 Types of fluid

• Ideal fluid-Fluid which is incompressible and have no viscosity.
• Real fluid-Fluid having viscosity.
• Newtonian fluid-Real fluid in which shear stress is directly proportional to rate of shear strain.
• Non-newtonian fluid- Real fluid in which shear stress is not directly proportional to rate of shear strain.

2.1.2 Laminar and turbulent flow

• A flow in which particles move in well-defined path or stream line is called laminar flow.
• A flow in which fluid move in zigzag motion is called turbulent flow.
• Reynold’s number is used to decide whether a flow is laminar or turbulent.

Where 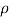=density,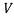=velocity,D=diameter of pipe,=viscosity

• Re>2300 flow is turbulent else it is laminar.

2.1.3 Newton’s law of cooling

Rate of convective heat transfer is determined by Newton’s law of cooling.

It states that rate of heat transfer is proportional surface area perpendicular to heat flow direction and temperature difference between wall surface (Tw) and fluid temperature (T∞) in direction perpendicular to flow.

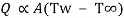
...(2.1)

Where, Q is rate of heat transfer (W), A is area in m2, h is constant known as coefficient of convective heat transfer or film coefficient with unit W/m2K.

Key Takeaways:

• The process of heat transfer between a solid surface and fluid in motion is called convection.
• Real fluid in which shear stress is not directly proportional to rate of shear strain.
• It states that rate of heat transfer is proportional surface area perpendicular to heat flow direction and temperature difference between wall surface (Tw) and fluid temperature (T∞) in direction perpendicular to flow.

2.2 Forced convection and natural convection:

Natural convection-

The convection in which fluid moves due to density difference caused by heat transfer between solid surface and fluid it said to be natural or free convection.

Natural convection is a sort of flow, of movement of a liquid along with water or a fuelling along with air, wherein the fluid movement isn't always generated through any outside source (like a pump, fan, suction device, etc. ) however through a few components of the fluid being heavier than different components. In maximum instances this ends in herbal circulation, the cap potential of a fluid in a gadget to flow into continuously, with gravity and viable modifications in warmness energy. The using pressure for herbal convection is gravity. For instance if there's a layer of bloodless dense air on pinnacle of warmer much less dense air, gravity pulls extra strongly at the denser layer on pinnacle, so it falls even as the warmer much less dense air rises to take its place. This creates circulating flow: convection.

As it is based on gravity, there's no convection in free-fall (inertial) environments, along with that of the orbiting International Space Station. Natural convection can arise whilst there are warm and bloodless areas of both air or water, due to the fact each water and air grow to be much less dense as they may be heated.

Forced convection-

If fluid motion is imparted by external means like pump is called forced convection.

This is a simplification of the concept that warm fluids are nearly constantly much less dense than the identical fluid whilst cold, however there are exceptions (see the layers of the surroundings and thermo hyaline flow for exceptions). This distinction in density makes warmer fabric certainly become on pinnacle of cooler fabric because of the better buoyancy of the warmer fabric.

In herbal convection, any fluid movement is precipitated via way of means of herbal manner consisting of the buoyancy effect, i.e. the upward push of hotter fluid and fall the cooler fluid. Whereas in pressured convection, the fluid is pressured to waft over a floor or in a tube via way of means of outside manner consisting of a pump or fan.

Key Takeaways:

• The using pressure for herbal convection is gravity.
• Natural convection can arise whilst there are warm and bloodless areas of both air or water, due to the fact each water and air grow to be much less dense as they may be heated.
• This distinction in density makes warmer fabric certainly become on pinnacle of cooler fabric because of the better buoyancy of the warmer fabric.

2.3 External and Internal flow convection:

External flow convection-Convection takes place as fluid flows over body with temperature difference.

In evaluation to inner go with the drift, outside flows function exceedingly viscous outcomes constrained to unexpectedly growing “boundary layers” with inside the front vicinity, or to skinny shear layers alongside the stable surface.

In this vicinity velocity, temperature, and/or awareness does now no longer extrude in and their gradients can be neglected. This impact reasons the boundary layer to be increasing and the boundary-layer thickness pertains to the fluid’s kinematic viscosity. This is validated on the subsequent picture. Far from the frame the go with the drift is almost in viscid, it is able to be described because the go with the drift of a fluid round a frame this is absolutely submerged in it.

Internal flow convection- Convection takes place as fluid flows inside body with temperature difference.

In fluid dynamics, inner waft is a waft for which the fluid is limited with the aid of using a surface. Detailed information of behavior of inner waft regimes is of significance in engineering, due to the fact round pipes can face up to excessive pressures and consequently are used to bring liquids. Non-round ducts are used to move low-stress gases, which include air in cooling and heating systems. The inner waft configuration is a handy geometry for heating and cooling fluids utilized in power conversion technology which include nuclear energy plants. For inner waft regime an front location is typical. In this location a almost in viscid upstream waft converges and enters the tube.

Key takeaways:

• Convection takes place as fluid flows over body with temperature difference.
• This is validated on the subsequent picture.
• Non-round ducts are used to move low-stress gases, which include air in cooling and heating systems.

2.4 Dimensionless parameters and correlations for forced convection

The convection in which fluid moves due to motion imparted by external means like pump is called forced convection.

Convection heat transfer coefficient depends on large number of variables like density, dimension of pipe, viscosity etc. various methods are can be opted to find heat transfer. One of which is dimensionless analysis which deals with usage of characteristic dimensionless numbers.

2.4.1 Dimensionless numbers

• Nusselt number(Nu):

Dimensionless heat transfer coefficient. It is ratio of convection heat transfer to conduction in a fluid layer of thickness L.

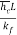…(2.2)

It measure energy transfer by convection occurring at surface.

If Nu=1, heat transfer is purely by conduction. Larger the value of Nu, larger will be rate of heat transfer by convection.

• Reynolds number(Re):

Ratio of inertia to viscous forces.

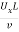…(2.3)

L=characteristic length which is equal to diameter in pipes. U=velocity and

It characterizes type of flow, whether laminar or turbulent.

• Prandtl Number(Pr):

Ratio of molecular momentum diffusivity to thermal diffusivity.

…(2.4)

Cp=specific heat, u=dynamic viscosity, 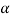=thermal diffusivity.

Higher the Pr higher is Nu and higher is the heat transfer.

• Stanton number(St):

It is dimensionless heat transfer coefficient. It is ratio of convective heat flux to heat transfer capacity.

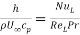…(2.5)

NuL=Nusselt number, ReL=Reynolds number for liquid, =density.

• Peclet number(Pe):

It is product of Reynolds and Prandtl numbers.

…(2.6)

2.4.2 Correlations for various shapes

Correlation between dimensionless numbers and convective heat transfer coefficient are used to determine heat flow rate.

2.4.2.1 Flow over the plate (External flow)

• For laminar flow

Local Nusselt number:

Average Nusselt number:

• For turbulent flow

Local Nusselt number: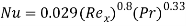

Average Nusselt number: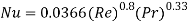

2.4.2.2 Flow through pipes (Internal flow)

• For laminar flow

(for constant heat flux)

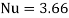(for constant wall temperature)

• For turbulent flow

When fluid is heated i.e. :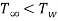

When fluid is cooled i.e.: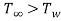

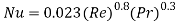
From value of Nusselt number, value of convective heat transfer coefficient can be found out which is then used to find heat transfer rate.

Mean film temperature=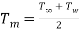

2.4.2.3 Characteristic length

Characteristic length also known as hydraulic diameter is important parameter for analysis of convection. As the geometry of conduit changes in internal flow, this length also changes. It is given as

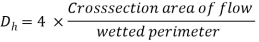
• For circular pipe

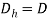
• For rectangular cross-section

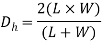
• For hollow pipe

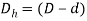
D=Outer diameter, d=inner diameter

2.4.3 Difference between average and local heat transfer coefficient

• Local heat transfer coefficient means that it is applicable at given point of solid body, over which fluid flow is taking place. Similarly local heat transfer coefficient applies to that particular point only.
• In practice, heat transfer rate would be required to found out over the entire surface hence, average heat transfer coefficient is used.
• Average heat transfer coefficient is found out by integrating local heat transfer coefficient over length of entire surface.

Key takeaways:

• One of which is dimensionless analysis which deals with usage of characteristic dimensionless numbers.
• Larger the value of Nu, larger will be rate of heat transfer by convection.
• It is dimensionless heat transfer coefficient. It is ratio of convective heat flux to heat transfer capacity.

2.5 Dimensionless parameters and correlations for natural(free) convection

The convection in which fluid moves due to density difference caused by heat transfer between solid surface and fluid it said to be natural or free convection.

2.5.1 Mechanism of natural convection

• When the air comes in contact with hot surface, its molecule in immediate vicinity of surface receives heat from hot surface. This causes temperature of molecules and its volume to increase.
• The density of air decrease due to increase in temperature of air adjacent to surface. Thus hot air rises under the action of buoyancy forces.
• The place of hot air is taken by heavier molecules which will also rise in similar manner on receiving energy from hot surface.
• This way natural motion in molecules is set and hence heat transfer is called natural convection.

2. 5.2 Coefficient of volumetric expansion

The coefficient of volumetric expansion is defined as density of fluid variation per degree change in temperature at constant pressure. It is denoted by 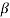and equal to

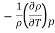…(2.7)

Negative sign since density decrease with increase in temperature. For ideal gas

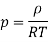
Therefore,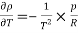

Higher value of 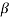higher will be density gradient hence higher heat transfer rate.

2.5.3 Dimensionless numbers

• Grashoff number(Gr):

It represents the product of buoyant and inertia forces to the square of viscous force.

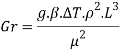
The role of Grashoff number in natural convection is similar to role of Reynolds number in forced convection. It provides criteria to decide whether flow is laminar or turbulent.

• Rayleigh number(Ra):

It is defined as product of Grashoff number and Prandtl number.

2.5.4 Correlations for various shapes

• Vertical plates and cylinders

Nu=0.59(Gr.Pr)0.25 when 104<Gr.Pr<109

Nu=0.13(Gr.Pr)0.33 when 109<Gr.Pr<1012

• Horizontal plates

Nu=0.54(Gr.Pr)0.25 when 105<Gr.Pr<2 x 107

Nu=0.15(Gr.Pr)0.33 when 2 x 107<Gr.Pr<3 x 1010

Comparison between Forced and natural convection

Key Takeaways:

• This causes temperature of molecules and its volume to increase.
• The coefficient of volumetric expansion is defined as density of fluid variation per degree change in temperature at constant pressure
• It represents the product of buoyant and inertia forces to the square of viscous force.

2.6 Correlations for forced and free convection-Approximate solutions to laminar boundary layer equations (momentum and energy) for both internal and external flow

The laminar boundary is a totally easy waft, whilst the turbulent boundary layer incorporates swirls or "eddies. The laminar waft creates much less pores and skin friction drag than the turbulent waft, however is much less stable. Boundary layer waft over a wing floor starts off evolved as a easy laminar waft.

To hire boundary layer ideas in actual engineering designs, we want approximate techniques that might speedy result in a solution although the accuracy is relatively less. Karman and Pohlhausen devised a simplified technique with the aid of using pleasurable simplest the boundary situations of the boundary layer go with the drift as opposed to pleasurable Prandtl's differential equations for every and each particle inside the boundary layer. We shall speak this technique herein.

In many realistic packages is isn't important to decide the “exact” answers of the boundary equations: its miles sufficient to recognize the end result to “within some percent”.

Approximate answers to the boundary–layer equations may be obtained with inside the following manner. The crucial members of the family of the boundary layer derived in Sect. 7.6 are used as a basis here. They may be study as everyday differential equations for, for example, the displacement thickness δ1 or the momentum thickness δ2, in addition to for the wall shear pressure we and the dissipation crucial D.

In order to collect further equations of motion, we want an approximation assumption: we think that the speed profiles all come from one “profile own circle of relatives”, i.e. they may be from a given quantity of feasible profiles. They range from different individuals of the own circle of relatives with the aid of using one or greater parameters, subsequently the expressions single–parameter or multi–parameter profile own circle of relatives.

These assumptions result in members of the family between the boundary function values and the profile parameters, which accordingly continue to be as features alongside the boundary layer wanting to be found. The quantity of equations which then want to be introduced to the crucial members of the family therefore relies upon immediately at the quantity of profile parameters.

 As we've got already mentioned, the numerous critical strategies fluctuate in particular in the profile own circle of relatives prescribed. Frequently a energy ansatz is used to describe the rate profile. In the primary critical approach ever used, a fourth order polynomial changed into applied. When the boundary situations have been taken into account this results in a single–parameter profile own circle of relatives

With the similarity variables from Eq.

We find the following relations for the boundary–layer characteristic quantities appearing in Eq. With the parameter β:

Displacement thickness eq.

Momentum thickness eq.

Wall shear stress:

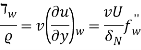
Here the quantities β1(β), β2(β) and fw” w(β) are all functions of the parameter β, as can also be seen from Table. The quantity δN is a measure of the boundary–layer thickness. It is proportional to the thickness δ99, where the constant of proportionality β99 still depends on β, cf. Table 8.1.

We have,

δ99 = β99δN

Key Takeaways:

• Approximate answers to the boundary–layer equations may be obtained with inside the following manner.
• The quantity of equations which then want to be introduced to the crucial members of the family therefore relies upon immediately at the quantity of profile parameters.
• When the boundary situations have been taken into account this results in a single–parameter profile own circle of relatives

2.7 Estimating heat transfer rates in laminar and turbulent flow situations using appropriate correlations for forced and free convection

• Laminar flow over flat plate:

Laminar go with the drift over a flat plate is a hassle that has been studied extensively, each analytically and experimentally. A option to a simplified shape of this hassle may be received whilst numerous assumptions are made. These assumptions had been first supplied via way of means of Blasius in 1908. Comparisons of experiments with this answer have proved to be accurate. Consider a go with the drift at pace U beyond a skinny plate of duration L. The time a fluid particle spends close to the frame is about L/U, at the same time as the time required for viscous results to unfold throughout the streamlines is of order.

This means that the Reynolds quantity need to be huge enough. This situation is understood to maintain genuine with inside the area 1000< Re < 106 out of doors of which the go with the drift will become turbulent.

The Blasius answer assumes that there may be an internal boundary layer area beneath an outer area at which the go with the drift stays similar to unfastened circulation conditions. A numerical simulation is installation to simulate the identical conditions.

Average friction coefficient

Local friction coefficient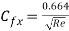

Thickness of boundary layer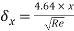

Thickness of thermal boundary layer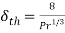

• Turbulent flow over plate:

Empirical correlations derived from the ones experiments, including the established regulation of the wall, are vital in derivations of turbulent version formulations and validations of turbulent version implementations in CFD codes.

Turbulent float over a 0 stress gradient flat plate is a not unusual place check case for the verification of turbulence fashions in CFD solvers. The float is anywhere turbulent and a boundary layer develops over the floor of the flat plate.

Average friction coefficient

Local friction coefficient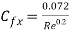

Thickness of boundary layer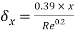

Key Takeaways:

• An option to a simplified shape of this hassle may be received whilst numerous assumptions are made.
• This situation is understood to maintain genuine with inside the area 1000< Re < 106 out of doors of which the go with the drift will become turbulent.
• Turbulent float over a 0 stress gradient flat plate is a not unusual place check case for the verification of turbulence fashions in CFD solvers.

References:

1. Bejan, Heat Transfer John Wiley, 1993
2. J.P. Holman, Heat Transfer, Eighth Edition, McGraw Hill, 1997.
3. F.P. Incropera, and D.P. Dewitt, Fundamentals of Heat and Mass Transfer, John Wiley, Sixth Edition, 2007.
4. Massoud Kaviany, Principles of Heat Transfer, John Wiley, 2002
5. Yunus A Cengel, Heat Transfer: A Practical Approach, McGraw Hill, 2002