Unit -3

Interaction of radiation with materials

3.1 Interaction of radiation with material

Introduction

• Thermal radiation refers to the radiant energy emitted by bodies by virtue of their own temperatures, resulting from the thermal excitation of the molecules.
• Radiation travels at the speed of light.The wavelength and frequency of radiation propagating in a medium are related by

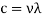
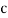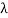Where =speed, =frequency and =wavelength

• The electromagnetic spectrum covering a wide range of wavelengths from less than 10-10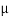m for cosmic rays to more than 1010m for electrical power waves includes gamma rays, X-rays, ultraviolet radiation, visible light, infrared radiation, thermal radiation, microwaves and radio waves.
• The type of electromagnetic radiation that is pertinent to heat transfer is the thermal radiation emitted as a result of vibration and rotational motions of molecules, atoms and electrons of a substance, and higher the temperature, higher is the rate of emission.
• It is the portion of electromagnetic spectrum that extends from 0.1 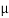m to 100 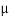m wavelength range.

3.2 Definitions of radiative properties

Properties of Radiation

• Reflectivity-It is defined as fraction of total incident radiations that are reflected by material.

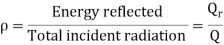
• Absorpivity-It is defined as fraction of total incident radiations that are absorbed by materials.

• Transmissivity-It is defined as fraction of total incident radiation that are transmitted by through material.

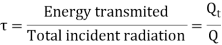
From law of conservation of energy,

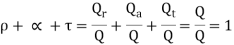
…(3.1)

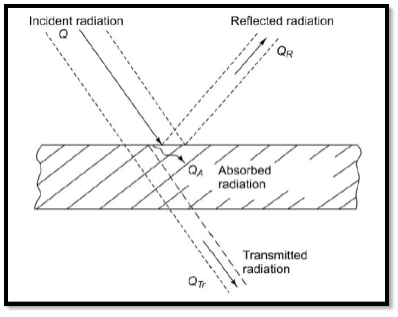
Fig.1 Radiation incident on a surface

3.3 Stefan Boltzmann’s law, black and gray body radiation

Types of bodies

• Black body-The body which absorbs entire radiations and emits maximum radiations is called a black body.

It implies that ,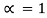

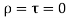
No perfect black body exist.

• Opaque body- The bodies or surfaces which have negligible transmissivity of energy are called opaque bodies e.g. Solid and liquid surface.                                        By opaque surface the radiant energy received is either absorbed or reflected i.e.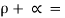1 and

• White body-The surface which reflects total radian energy are called white bodies.

For such bodies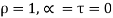

• Grey body-The body which has its absorptivity equal to its emissivity is called a grey body provided the temperature of the surface of incident radiation and the body are same.

1. Emissive power

The total emissive power of a body, E, is defined as the total radiant energy emitted by the body at a certain temperature per unit time and per unit surface area at all wavelengths.

Where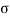 = 5.67x 10-8 W/m2 K4 is called the Stefan–Boltzmann constant and T is the absolute temperature of the surface in kelvin.

2.     Emissivity

The emissivity of a surface is defined as the ratio of radiation emitted by the surface to the radiation emitted by a black body at the same temperature.

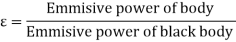
It is denoted by 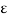, and it varies between 0 and 1. Emissivity is a measure of how closely a surface approximates a black body for which 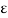= 1.

Monochromatic emissive power is ratio of monochromatic emissive power of a body to monochromatic emissive power of black body and denoted by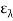

3.     Planck’s Law

Planck’s law is based on quantum theory. It states that for monochromatic emissive power of black body as function of absolute temperature.

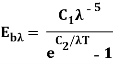
Where C1=3.742 x 10-16 W/m2 C2=1.438 x 10-2 m/K, 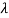is wavelength.

4.     Stefan–Boltzmann Law

It states that total emissive power of black body is directly proportional to fourth power of absolute temperature.

Planck’s law also permits to derive Stefan–Boltzmann law, which establishes the dependence of total hemispherical radiation on temperature.

The total emissive power of a black body is given by

Substituting

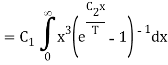
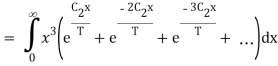
Since

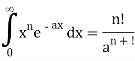
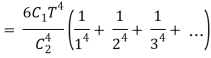
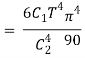
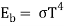
Where 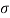is the Stefan-Boltzmann constant.

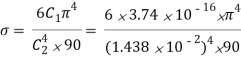
=5.67  X 10-8 W/m2 K4

5.     Wien’s displacement law

Wien’s displacement law gives relationship between maximum wavelength 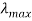at which maximum monochromatic emissive power is obtained and the absolute temperature T for black body.

According to this law,

Where

6.     Kirchhoff’s law

It states that the emissivity of the surface is equals to its absorptivity when the surface or the body is in thermal equilibrium with surrounding.

3.4 Calculation of radiation heat transfer between surfaces using

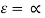
Radiative properties

Intensity of radiation

The intensity of radiation, I is defined as the rate of heat radiation in a given direction from a surface per unit solid angle per unit area of the projection of the surface on a plane normal to the direction of radiation.

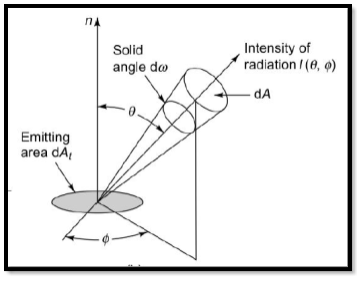
Fig2 Intensity of radiation

A solid angle is defined as the ratio of the spherical surface enclosed by a cone, with its vertex at the centre of the sphere, to the square of the radius of the sphere.

The solid angle subtended by the spherical surface dA at the centre would be dA/r2, where r is the radius of the sphere.

Intensity is given as

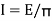…(3.2)

Where E=emissive power of body.

Radiant heat exchange between two black bodies

The radiant heat exchange between two bodies depends upon

• The views the surfaces have of each other
• Their emitting and absorbing characteristics and
• The medium that intervenes the two bodies.

Let us assume that the two bodies are black and the medium is nonparticipating in the energy exchange. Let us consider the area elements dA1 and dA2on the two surfaces. The distance between them is r and the angles made by the normals to the two area elements with the line joining them are and respectively. The projected area of dA1 in the direction of radiation is.

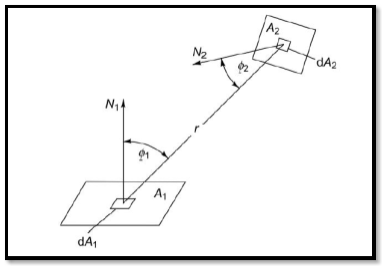
Fig3 Radiant heat exchange between 2 black surfaces

Energy leaving dA1 and intercepted (and absorbed, since the surface is black) by dA2 is

DQ1-2 = I1 dA1 cos 1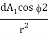 

Where the solid angle subtended by the element dA1 at the centre of dA1 is (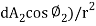. Since I1 is independent of the direction, the energy emitted per unit of area dA1 per unit solid angle is proportional to the cosine of the angle . This is known as Lambert’s cosine law. From eq 3.2

DA2dQ1 – 2 = 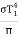dA1 cos 1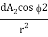 

The total radiation leaving A1 and being absorbed by A2 is

Q1 – 2 =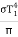

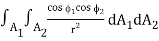
= A1 F12 σT14                       …..(3.3)

Where      A1F12 = 1/π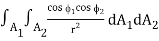

Similarly, energy leaving dA2 and intercepted (and absorbed) by dA1 is

DQ2 – 1 = I2 dA2 cos 2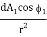 

=

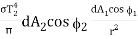
Therefore total radiation leaving A2 and being absorbed by A1 is

Q2-1 =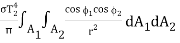

= A2F21 σT24   …(3.4)

Where

A2 F21 = 1/π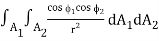

Net energy exchange between A1 and A2 using 3.3 and 3.4

(Q12)net = Q1-2 – Q2-1

= σA1 F12 (T14 – T14)   …(3.5)

And also

A2 F21 = A2F21 = 1/π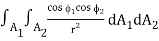

…(3.6)

Here, F12 is called the shape factor of A1 with respect to A2. This is the fraction of energy leaving A1 thatstrikes A2 (and is absorbed, because the surface is black). Similarly, F21 is the shape factor of A2 with respect to A1, which is also the fraction of energy leaving A2 that strikes A1 (and is absorbed). Since the values of F12 and F21 depend on how the two surfaces are exposed to each other or “see” each other, these are also called view factors, geometry factors or configuration factors. Unless A1 is equal to A2,. But

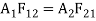…(3.7)

This is known as reciprocity theorem.

7.     Shape Factor

• Shape factor is defined as fraction of energy emitted by one surface and directly intercepted by another surface.
• It is also called as view factor or angle factor.
• It depends upon size and shape of surfaces, orientation and distances between them.
• Reciprocal relationship between two shape factors is given in eq. 3.7.

Enclosure theorem

Consider an enclosure of n surfaces and each is maintained at different temperatures. Each surface will exchange radiant energy with n surfaces including itself. Hence,

F11 + F12 + F13 + . . . + F1n =1

F21 + F22 + F23 + . . . + F2n = 1

.

.

.

Fn1 + Fn2 + Fn3 + . . . + Fnn = 1

…(3.8)

This is known as enclosure theorem. It holds true for every surface.

Shape factor for standard configurations

Hemispherical shape

A surface has a shape factor with respect to itself if it is concave, because some of the emitting radiation will be intercepted by the surface itself. If the surface is flat or convex, the shape factor with respect to itself is zero.Let us consider a hemispherical black cavity with a flat black plate over it. The surface of the cavity is denoted by 1 and that of the plate by 2. Then

F11 + F12 =1

F21 + F22 = 1

But F22 = 0, therefore, F21 = 1

A1F12 = A2F21 = A2

Fig4 Radiation in a hemispherical cavity

F12 = A2/A1

F11 = 1 – A2/A1 = 1 – πr2/2πr2 =1/2

Therefore, 50% of radiation emitted from the hemispherical surface is striking the surface itself, and is absorbed.

Two concentric cylinders

In two concentric black cylinders, if 1 represents the outer surface of the inner cylinder and 2 represents the inner surface of outer cylinder then,

Fig5 Radiant heat exchange between concentric cylinders

F11 + F12 = 1,

F11 = 0.

F12 = 1,

A1 F12 = A2F21, F21 = A1/A2

F21 + F22 = 1

F22 = 1 – A1/A2 = 1 – (πd1L)/(πd2L) = 1 – d1/d2

Therefore fraction of 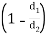of radiations will fall back on surface 2.

Electrical analogy

The black enclosure may be represented by an analogous electrical network. The rate of radiant flux between two black surfaces may be written as

Q1-2 = σA1F12 (T14 – T24)

=

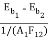
Where (according to Stephan-Boltzmann law)

(Eb1 – Eb2) is the driving force or potential between the two nodes 1 and 2 forradiative energy transfer and (1/A1 F12) is the resistance. The corresponding network is given in Fig.

Fig6 Electrical analogy of radiative energy transfer between two black surfaces 1 and 2

Similarly for 4 wall enclosure

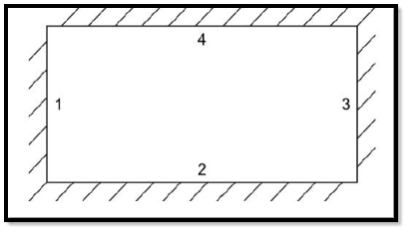
Fig7. Radiative flux between the walls of a four-wall black enclosure

(Q1)net = σ A1F12(T14 – T24) + σ A1 F13(T14 – T34) + σA1F14(T14 – T44)

(Q1)net =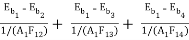 

Radiant heat exchange between two grey bodies

Let us consider two gray bodies, represented by suffices 1 and 2, having emissivity’s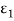and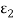. Let us suppose that the bodies are small compared with the distance between them. It may thus be assumed that of the radiation unabsorbed and reflected diffusely at each surface, a negligible proportion returns to the original emitting body.

The energy emitted by the body 1 is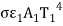, of which F12 (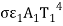) is incident on the second body, of which (F12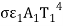) is absorbed(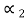is absorptivity). Since the bodies are gray, 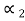= 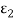and energy transfer from 1 to 2 is

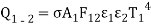
Similarly

Therefore, the net radiant heat transfer between the two bodies is

(Q1-2)net = σ A1F12 1 2(T14 – T24)

The equivalent emissivity of two small gray bodies is

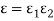
Radiosity and Irradiation

• Radiosity is the term used to indicate the total radiant energy leaving a surface per unit time and per unit surface area. It is denoted by the symbol J.
• This quantity differs from the emissive power in that the radiosity includes reflected energy as well as the original emission, regardless of any directional dependence or spectral preference.
• Irradiation is the term used to denote the total radiation incident on a surface per unit time and per unit surface area. It is denoted by the symbol G.

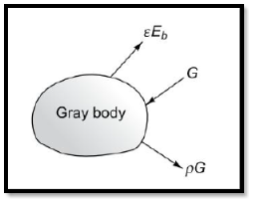
Fig8 Radiosity and irradiation in a gray body

The radiosity is the sum of the energy emitted and the energy reflected, when no energy is transmitted )

J =  Eb + G

=  Eb + (1 - )G

G = (J - Eb)/(1 - ) …(3.9)

Q/A = J – G =  Eb + (1 - )G – G

=  (Eb – G)

Substitute 3.9 in above equation

Q/A = (Eb – ) = 

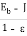
Qnet =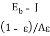

This equation provides a basis for network representation of the gray enclosure. If the numerator on the right side is considered as the potential difference, the denominator as the “surface resistance” to radiation heat transfer and the heat flow as current, then a network element could be drawn, as shown in Fig.

3.5 View factors and the radiosity method

Radiant heat transfer between grey bodies using radiosity method

Consider the exchange of radiant energy by two surfaces A1 and A2 Of the total radiation which leaves the surface 1, the amount that reaches surface 2 is J1A1F12, and of the total energy leaving surface 2, the amount that reaches surface 1 is J2A2F21

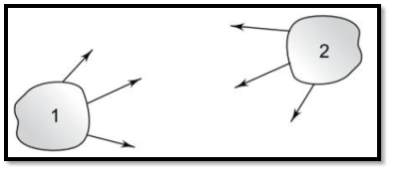
Fig9. Radiant interchange between two gray surfaces

Net energy interchange between two surfaces

Q1-2 = J1A1F2 – J2A2F21

= (J1 – J2)A1F12

Since  A1F12 = A2F21

Q-2 = 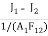             …(3.10)

The denominator of this equation is called space resistance and numerator is called potential difference.

Radiation heat transfer between two parallel bodies

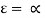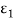The radiant interchange between two infinite parallel gray planes involves no geometry factor, since F12 = F21 = 1.0. Let us consider two gray planes, as shown in Fig. 7.34. For gray surfaces, and. Surface 1 emits Eb1per unit time and area. Surface 2 absorbs the fraction 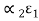Eb1or 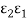Eb1 and reflects

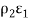Eb1 or 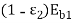back towards A1. The net heat transferred per unit of surface 1 to 2 is the emission 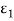Eb1minus the fraction of Eb1and 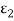Eb2 which is ultimately absorbed by surface 1 after successive reflections. Therefore,

(Q 1- 2)net = A 1Eb1 [ 1 - 1(1 - 2) - 1 ( 1- 1)(1 - 2)2 - 1 (1 - 1)2 (1 - 2)3 - . . . ]

- A2 2Eb2 [ 1 + 1 (1 - 1)(1 - 2) + 1(1 - 1)2 (1 - 2)2 + . . .]

= A1 1 Eb1 [ 1 – (1(1 - 2))/(1 – (1 - 1)(1 - 2))] + A2 2 Eb2  1/(1 – (1 - 1)(1 - 2))

= A (12)/(1 + 2 - 12)   (Eb1 – Eb2 )

Since A1 = A2 = A.

(Q1-2)net = A σ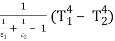

Or  (Q1 – 2)net = σ A F12 (T14 – T24 )

  where F12 =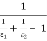

Where F12 is the view factor for gray bodies.

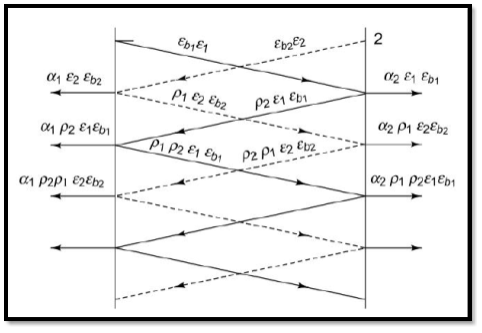
Fig9 Radiant heat exchange between two infinite parallel gray planes

Important formulae

Speed of radiation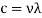
Reflectivity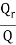
Absorptivity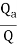
Transmisivity
Relation between reflectivity,absorptivity and transmisivity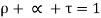
Emissive power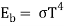
Emissive power of black body(Plank’s law)	Ebλ =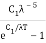
Solid angle	A/r2
Intensity of radiation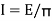
Net radiative heat exchange between black bodies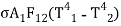
Heat exchange in form of electrical analogy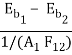
Radiation heat transfer between two parallel bodies	(Q1-2)net = Aσ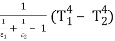

References:

1. Bejan, Heat Transfer John Wiley, 1993

2. J.P.Holman, Heat Transfer, Eighth Edition, McGraw Hill, 1997.

3. F.P.Incropera, and D.P. Dewitt, Fundamentals of Heat and Mass Transfer, John Wiley, Sixth Edition, 2007.

4. MassoudKaviany, Principles of Heat Transfer, John Wiley, 2002

5. Yunus A Cengel, Heat Transfer: A Practical Approach, McGraw Hill, 2002