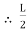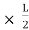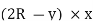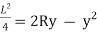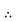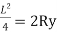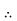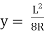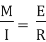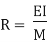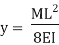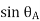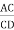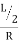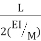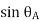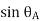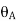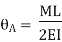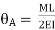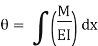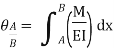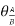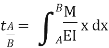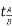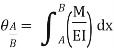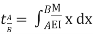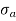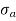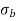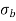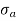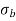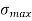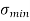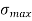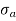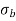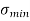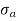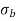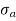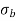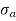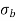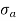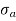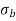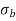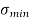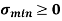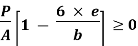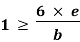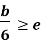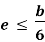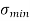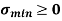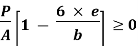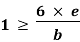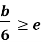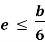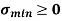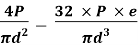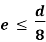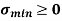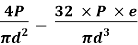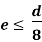4.1 Slope and Deflection – | unit 4 deflection of beams

Back to Study material

ISM

Unit - 4

Deflection of Beams

4.1 Slope and Deflection –

A) Slope –

It is angular shift at any point of the beam between no load condition and loaded beam.
Its value is different at different points on the length of the beam.
It is represented by dy/dx or θ.
Its unit is radians.
There is a maximum limit for slope for any loaded beam.

B) Deflection –

It is the vertical shift of a point on the beam between no load condition and loaded beam.
Its value is different at different points on the length of the beam.
It is represented by y or 𝜹.
Its units are mm.
There is a limit for maximum deflection for any loaded beam.

Key Takeaways-

Slope is angular shift at any point of the beam between no load condition and loaded beam.
Deflection is the vertical shift of a point on the beam between no load condition and loaded beam.

4.2 Relationship Between Moment, Slope and Deflection –

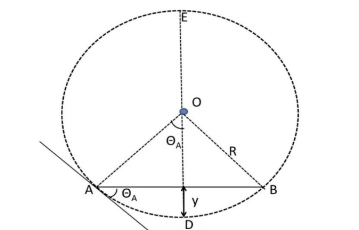
Let,

L = Span of Beam

M = Bending Moment

R = Radius of curvature of beam after bending

Y = Deflection of beam at centre

= Slope of beam

$C:\Users\DELL\AppData\Local\Microsoft\Windows\INetCacheContent.Word\Screenshot_20210118-090649__01__01.jpg$

Fig No 4.1

From the above figure,

AC BC = CE CD

In practice, deflection of beam y is very small and square of y is negligible.

............eq. no 1

By using Bending Formula,

Put the value of R in eq. no 1, we get

From the geometry of fig.

= = =

Since, is very small quantity =

Key Takeaways-

is the Relationship Between Moment, Slope and Deflection

4.3 Moment Area Method –

The moment-area theorem is an engineering tool to derive the slope, rotation and deflection of beams and frames.
This method is advantageous when we solve problems involving beams, especially for those subjected to a series of concentrated loadings or having segments with different moments of inertia.
If we draw the moment diagram for the beam and then divided it by the flexural rigidity(EI), the 'M/EI diagram' results by the following equation.

4.3.1 Theorem 1 –

The change in slope between any two points on the elastic curve equals the area of the M/EI (moment) diagram between these two points.

Where,

M = Moment

EI = Flexural Rigidity

= Change in slope between points A and B

A, B = Points on Elastic curve

4.3.2 Theorem 2 –

The vertical deviation of a point A on an elastic curve with respect to the tangent which is extended from another point B equals the moment of the area under the M/EI diagram between those two points (A and B). This moment is computed about point A where the deviation from B to A is to be determined.

Where,

M = Moment

EI = Flexural Rigidity

= deviation of tangent at point A with respect to the tangent at point B

A, B = Points on Elastic curve

4.3.3 Rules of Sign Convention –

The deviation of any point is positive if the point lies above the tangent, negative if the point is below the tangent.
Measured from left tangent, if anticlockwise, the change of slope is positive, if is clockwise.

4.3.4 Procedure of Analysis –

The following procedure provides a method that may be used to determine the displacement and slope at a point on the elastic curve of a beam using the moment-area theorem.

Determine the reaction forces of a structure and draw the M/EI diagram of the structure.
If there are only concentrated loads on the structure, the problem will be easy to draw M/EI diagram which will result a series of triangular shapes.
If there are mixed with distributed loads and concentrated, the moment diagram (M/EI) will results parabolic curves, cubic, etc.
Then, assume and draw the deflection shape of the structure by looking at M/EI diagram.
Find the rotations, change of slopes and deflections of the structure by using the geometric mathematics.

Key Takeaways-

Theorem 1 –

The change in slope between any two points on the elastic curve equals the area of the M/EI (moment) diagram between these two points.

Theorem 2 –

4.4 Macaulay’s method –

When the beam is subjected to point loads (but several loads) this is very convenient method for determining the deflection of the beam.
In this method we will write single moment equation in such a way that it becomes continuous for entire length of the beam in spite of the discontinuity of loading.
After integrating this equation, we will find the integration constants which are valid for entire length of the beam. This method is known as method of singularity constant.

4.4.1 Procedure of Analysis –

Step – I:

Calculate all reactions and moments.

Step – II:

Write down the moment equation which is valid for all values of x. This must contain brackets.

Step – III:

Integrate the moment equation by a typical manner. Integration of (x-a) will be 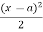not 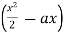and integration of 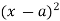will be 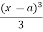and so on.

Step – IV:

After first integration write the first integration constant (A) after first terms and after second time integration write the second integration constant (B) after A.x. Constant A and B are valid for all values of x.

Step – V:

Using Boundary condition find A and B at a point x = p if any term in Macaulay’s method, (x-a) is negative (-ve) the term will be neglected.

Key Takeaways-

1. Procedure of Analysis –

Step – I:

Calculate all reactions and moments.

Step – II:

Write down the moment equation which is valid for all values of x. This must contain brackets.

Step – III:

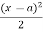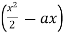Integrate the moment equation by a typical manner. Integration of (x-a) will be not and integration of 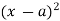will be 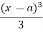and so on.

Step – IV:

Step – V:

Using Boundary condition find A and B at a point x = p if any term in Macaulay’s method, (x-a) is negative (-ve) the term will be neglected.

4.5 Buckling and Stability –

A) Buckling –

Buckling is the sudden change in shape (deformation) of a structural component under load, such as the bowing of a column under compression or the wrinkling of a plate under shear.

If a structure is subjected to a gradually increasing load, when the load reaches a critical level, a member may suddenly change shape and the structure and component is said to have buckled.

B) Stability –

Stability is the ability of the structure to support a specified load without undergoing unacceptable (or sudden) deformations.

Key Takeaways-

Buckling is the sudden change in shape (deformation) of a structural component under load, such as the bowing of a column under compression or the wrinkling of a plate under shear.
Stability is the ability of the structure to support a specified load without undergoing unacceptable (or sudden) deformations.

4.6 Slenderness Ratio –

The ratio of the effective length of a column to the least radius of gyration of its cross section is called the slenderness ratio (sometimes expressed with the Greek letter lambda, λ).
This ratio affords a means of classifying columns and their failure mode.
The slenderness ratio is important for design considerations. All the following are approximate values used for convenience.

Key Takeaways-

The ratio of the effective length of a column to the least radius of gyration of its cross section is called the slenderness ratio (sometimes expressed with the Greek letter lambda, λ).

4.7 Combined Bending and Direct Stress –

Direct Stresses alone is produced in a body when it is subjected to an axial tensile or compressive load, and Bending stress is produced in the body when it is subjected to bending moment.
But if a body is subjected to axial loads and bending moments, then both the stresses will be produced in the body. Therefore,
The Direct stress (or) Axial

= Load/ Area

=P/A

The Bending stress

= + Moment at the section / Section Modulus

= + M/Z

Where e is eccentricity of load P, M is bending moment and Z is the section modulus about bending axis.
When a column of rectangular section is subjected to an eccentric load the section is subjected both direct stress and bending stress. the Resultant stresses due to the combined Bending and Direct Stress are,

σ = +

σ = P/A + M/Z

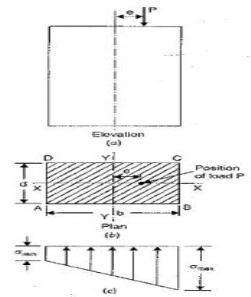
Fig No 4.2 Combined Bending and Direct Stress

= P/A + M/Z

= P/A - M/Z

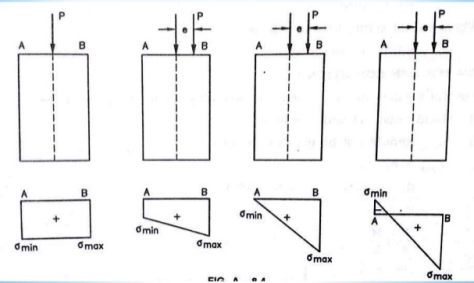
The stress distribution form face A to face B as shown in the figure.

= +

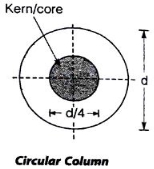
Fig No 4.3 Stress Distribution

Note:

1.Eccentric load produces direct stress as well as bending stress.

2. If direct stress is more than bending stress ( greater than ), then the stress throughout the section will be compressive

3.If direct stress is equal to bending stress ( = ), then the tensile stress will be zero.

4.If direct stress is less than bending stress ( less than ), then there will be tensile stress.

5.Hence for no tensile stress in the section, the direct stress will be greater than or equal to bending stress.

Key Takeaways-

The Direct stress (or) Axial

= Load/ Area

=P/A

The Bending stress

= + Moment at the section / Section Modulus

= + M/Z

4.8 Middle Third Rule –

For a rectangular section there will be no tensile stress if the load is on either axis within the middle third of the section.

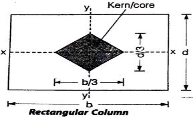
Fig No 4.4 Rectangular Column

The minimum stress () must be greater or equal to zero for no tensile stress at any point along the width of the column.

Therefore, we can say that if load will be applied with an eccentricity equal to or less than b/6 from the axis YY and on any side of the axis YY then there will not be any tensile stress developed in the column.
Hence range within which load could be applied without developing any tensile stress at any point of the section along the width of the column will be b/3 or middle third of the base.
Similarly, in order to not develop any tensile stress at any point in the section along the depth of the column, eccentricity of the load must be less than or equal to (d/6) with respect to axis XX.
Therefore, we can say that if load will be applied with an eccentricity equal to or less than d/6 from the axis XX and on any side of the axis XX then there will not be any tensile stress developed in the column.

Key Takeaways-

The minimum stress () must be greater or equal to zero for no tensile stress at any point along the width of the column.

4.9 Middle Quarter Rule –

For a circular section there will be no tensile stress if the load is on either axis within the circle of diameter equal to one-fourth of the main section diameter.

Fig No 4.5 Circular Column

If load will be applied with an eccentricity equal to or less than d/8 from the axis XX and on any side of the axis XX then there will not be any tensile stress developed in the circular section.
Hence range within which load could be applied without developing any tensile stress at any point of the section will be d/4 or middle quarter of the main circular section.
Area of the circle of diameter d/4 within which load could be applied without developing any tensile stress at any point of the section will be termed as Kernel of the section.

Key Takeaways-

For a circular section there will be no tensile stress if the load is on either axis within the circle of diameter equal to one-fourth of the main section diameter.

References-

Mechanics of Materials by Hibbeler,Pearson.
Mechanics of Materials by Gere,Cengage Learning.
Strength of Materials by Ryder,Macmillan.
Mechanics of Materials by Patel, Cengage Learning.

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined