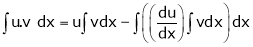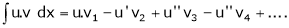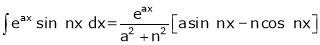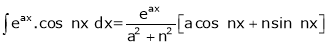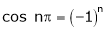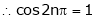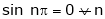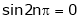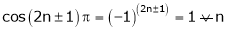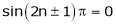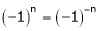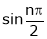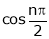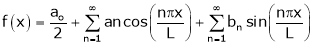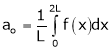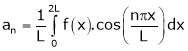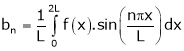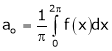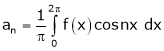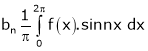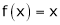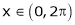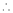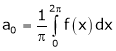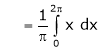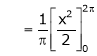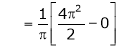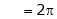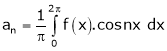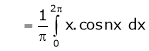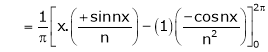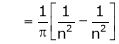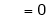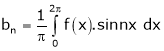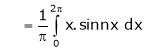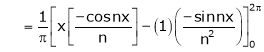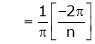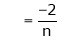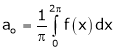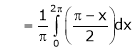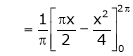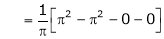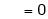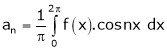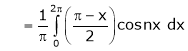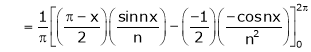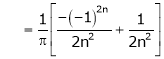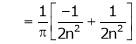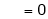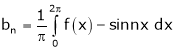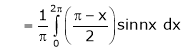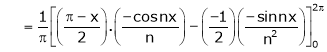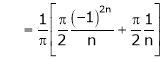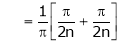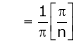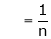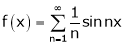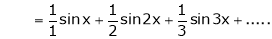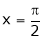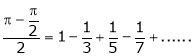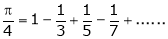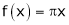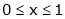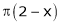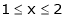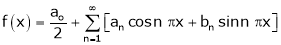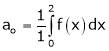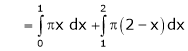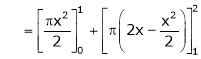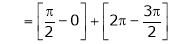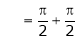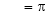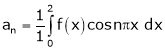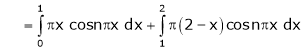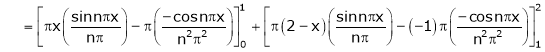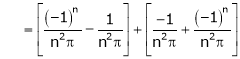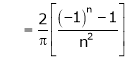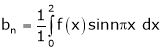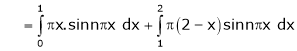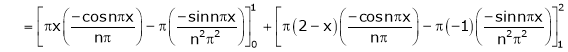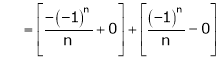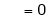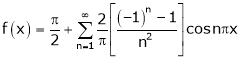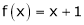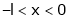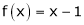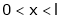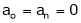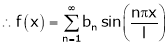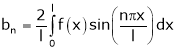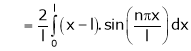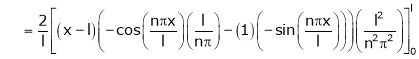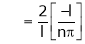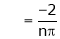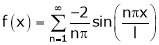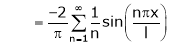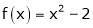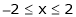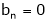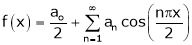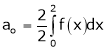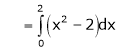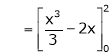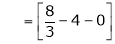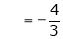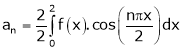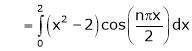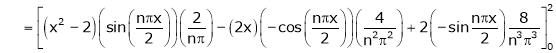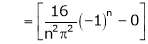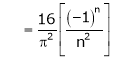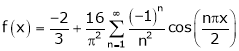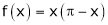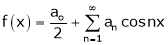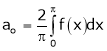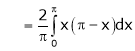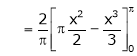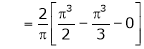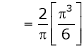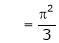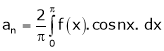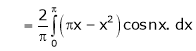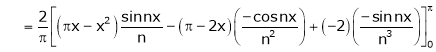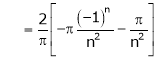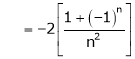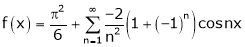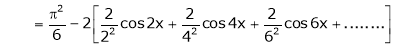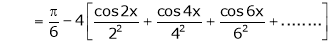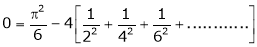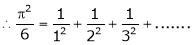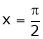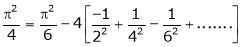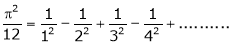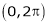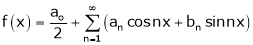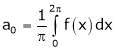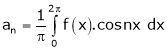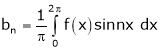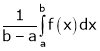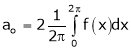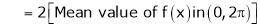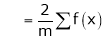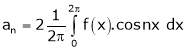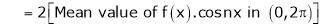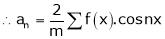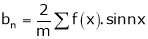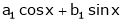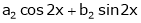Unit - 2
Fourier Series
In last semester we find expansions of functions by using Taylor’s series as well as Maclaurin’s series. Now here we express a special type of function in terms of sines and cosines are called as a Fourier Series.
Periodic Function:
A function is called periodic if it is defined every real x and if there exist a some positive integer ‘T’ such that 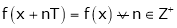 , n = 1, 2, 3, ……
, n = 1, 2, 3, ……
The number ‘T’ is called period of the function f(x). i.e. The graph of f(x) repeats after the interval T.
e.g. sin x or cos x are periodic functions of period 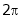 .
.
Note:
If ‘T’ is a period of function f(x) then 2T, 3T, 4T, ….. are also periods of f(x). The smallest of all these is called as primitive period of f(x).
Important formulas to evaluating integrals
Where dashes indicates derivatives and suffixes indicates integrations. 3. 2. sin A. cos B = sin (A + B) + sin (A – B) 2. cos A. sin B = sin (A + B) + sin (A – B) 2. cos A. cos B = cos (A + B) + cos (A – B) 2. sin A. sin B = cos (A – B) – cos (A + B) 4. 5. 6.
7.
8. 9.
|
Even and odd functions
- Even functions:-
A function f(x) is defined on the both sided interval i.e. on (-l, l) or 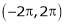 or
or 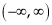 or
or 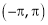 is said to be even if.
is said to be even if.
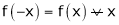
Also if
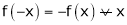 ; then f(x) is called odd function.
; then f(x) is called odd function.
e.g.
(i) f(x) = x2 is even function
(ii) f(x) = sin x is odd function.
Note:-
1) The addition or subtraction of two odd functions is again odd.
2) The addition or subtraction of two even functions is even.
3) The addition or subtraction of even and odd function neither odd nor even.
4) The product of two even functions is again even.
5) The product of two odd functions is also even.
6) The product of even and odd functions is odd.
Let f(x) be a function defined in C < x < C + 2L such that
1) f(x) is defined and single valued in the given internal also. 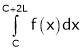 exist.
exist.
2) f(x) may have finite number of finite discontinuities in the interval.
3) f(x) may have finite number of maxima or minima in the given interval.
Definition:
Fourier Series
Let f(x) be a periodic function of period 2L. defined in the internal 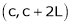 and satisfied Dirichlet's conditions, then f(x) can be expressed as,
and satisfied Dirichlet's conditions, then f(x) can be expressed as,
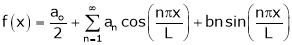 .
.
Where ao, an, bn are called Fourier constant’s or Fourier coefficients and are given by,
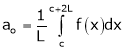
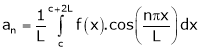
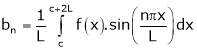
Note:
That there are only 4 intervals as below. i.e. 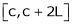 is divided into following four intervals.
is divided into following four intervals.
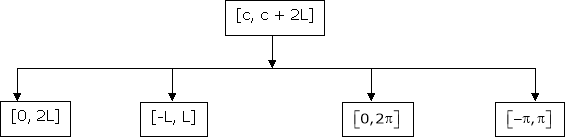
Note that for [0, 2L] we put c = 0 |
Hence Fourier series in this interval will be, |
|
Where |
|
|
|
Simillarly, for the interval |
Hence Fourier series in this interval will be |
|
Where |
|
|
|
Note that for the interval [-L, L] i.e. put C = -L, |
First we check whether f(x) is even function or odd. |
Case I:-
If f(x) is even function. Then we get half range cosine series as,
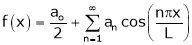
Where
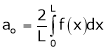
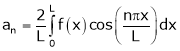
Case II:-
If f(x) is odd function. Then we get half range sine series as,
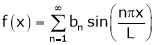
Where
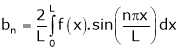
Simillarly
Note that for that interval 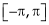 i.e. put
i.e. put 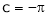 ,
, 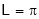
First we check wheatear f(x) is even or odd function.
Case I:-
If f(x) is even function then we get half range cosine series as
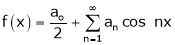
Where
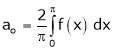
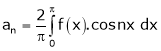
Case II:-
If f(x) is odd function then we get half range sine series as,
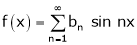
Where
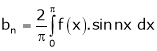
Note that
- For half range cosine series i.e. f(x) is even function bn = 0
- For half range sine series i.e. f(x) is odd function ao = an = 0
Q1)
Find the Fourier series of f(x) = x in the interval 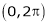
S1)
Here |
|
|
Where |
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
Hence the required Fourier series is |
|
Q1) Find the Fourier series for
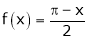 in the interval
in the interval 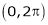
Hence deduce that
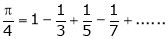
S1)
Here |
Hence it’s Fourier series is, |
|
Where |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Hence equation (1) becomes |
|
|
Put |
|
i.e. |
|
Q2) Find a Fourier series expansion in the interval 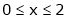 for
for
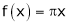 ;
; 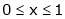
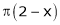 ;
; 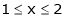
S2)
Here |
|
|
Hence it’s Fourier series expansion is, |
|
Where |
|
|
|
|
|
|
|
|
|
|
|
And |
|
|
|
|
|
Hence equation (1) becomes |
|
|
Q3) Find a Fourier series of
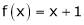 ;
; 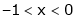
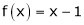 ;
; 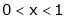
S3)
Here |
|
|
Here f(x) is odd function Hence we get half range sine series i.e. |
|
Where |
|
|
|
|
|
Hence equation (1) becomes, |
|
|
Q4) Find a Fourier series for
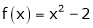 ;
; 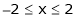
S4)
Here |
|
Since f(x) is even function hence |
|
|
Where |
|
|
|
|
|
|
|
|
|
|
Hence equation (1) becomes, |
|
Q5) Find half range cosine series of 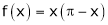 in the interval
in the interval 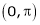 and hence deduce that
and hence deduce that
a) 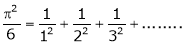
b) 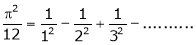
S5)
Here |
|
Hence it’s half range cosine series is, |
|
Where |
|
|
|
|
|
|
|
|
|
|
|
Hence equation (1) becomes, |
|
|
|
Put x = 0, we get |
|
|
Hence the result |
Put |
|
i.e. |
|
The Fourier expansion of any function f(x) in the interval |
|
Where |
|
|
|
Practically these functions are often not given by formula but by table of corresponding values. In such cases integral is cannot be evaluated and Hence we use mean value of the function |
|
Thus the above formulas becomes, |
|
|
|
Where m is the no of subintervals |
|
|
|
Simillarly, |
|
Here the term in (1) is |
|
Note that
- The amplitude of nth harmonic is
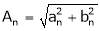
- The square of amplitude is called energy of the nth harmonic.
i.e. 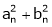 is called energy of the nth harmonic
is called energy of the nth harmonic
3. % of nth harmonic
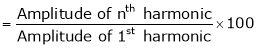
Exercise
- Find Fourier series for
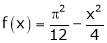 in
in 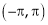 & Hence deduce that
& Hence deduce that
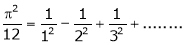
2. Find a Fourier series for
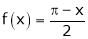 in the internal
in the internal 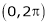 & hence deduce that
& hence deduce that
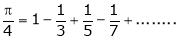
3. Find a Fourier series for
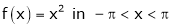 ,
,
Hence, show that
a) 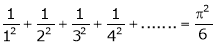
b) 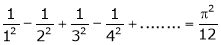
c) 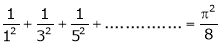
Find the Fourier series of the Function
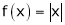 ;
; 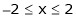
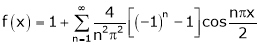
Find Half range cosine series of 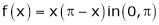 and Hence deduce that
and Hence deduce that
a) 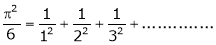
b) 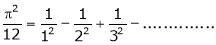
Find half range sine series of 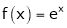 in
in 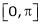 .
.
Reference Books:
1. Advanced Engineering Mathematics by Erwin Kreyszig (Wiley Eastern Ltd.)
2. Advanced Engineering Mathematics by M. D. Greenberg (Pearson Education)
3. Advanced Engineering Mathematics by Peter V. O’Neil (Thomson Learning)
4. Thomas’ Calculus by George B. Thomas, (Addison-Wesley, Pearson)
5. Applied Mathematics (Vol. I & Vol. II) by P.N.Wartikar and J.N.Wartikar Vidyarthi Griha Prakashan, Pune.
6. Linear Algebra –An Introduction, Ron Larson, David C. Falvo (Cenage Learning, Indian edition)