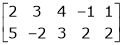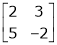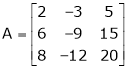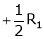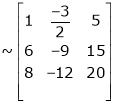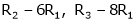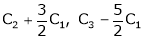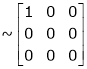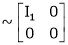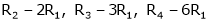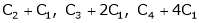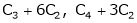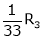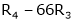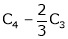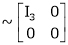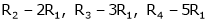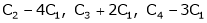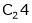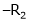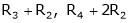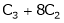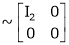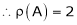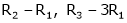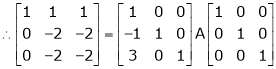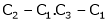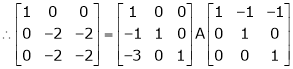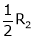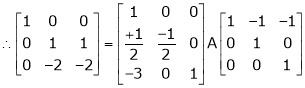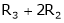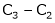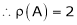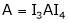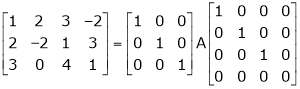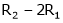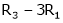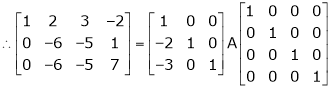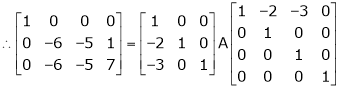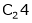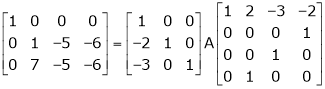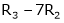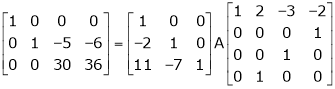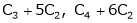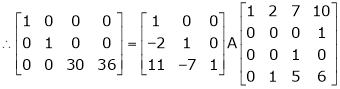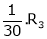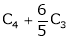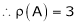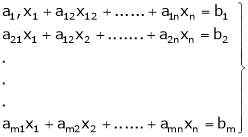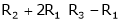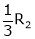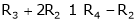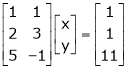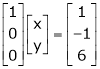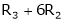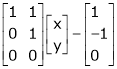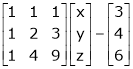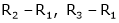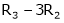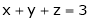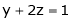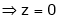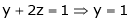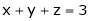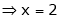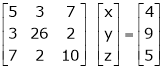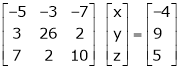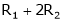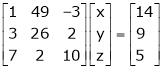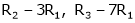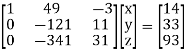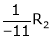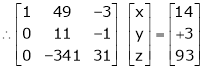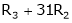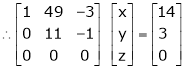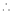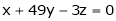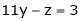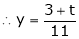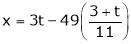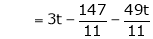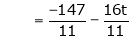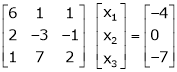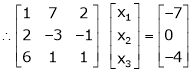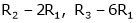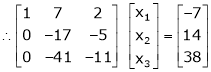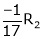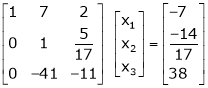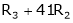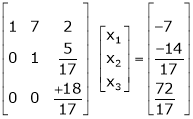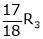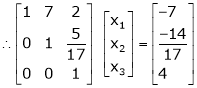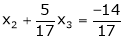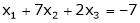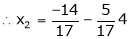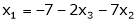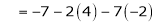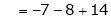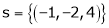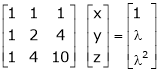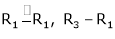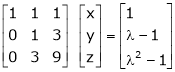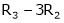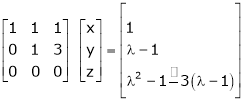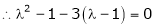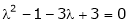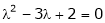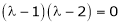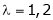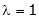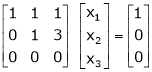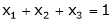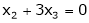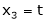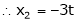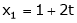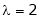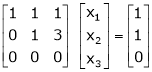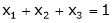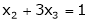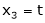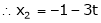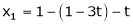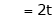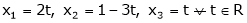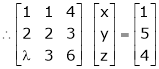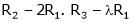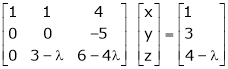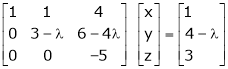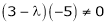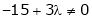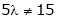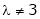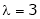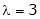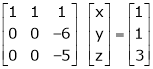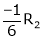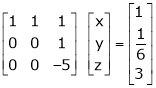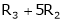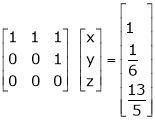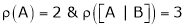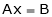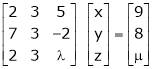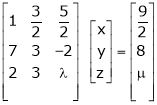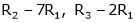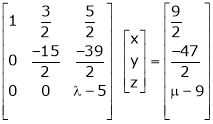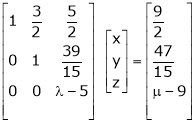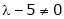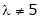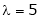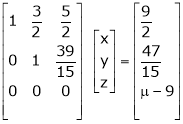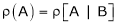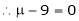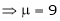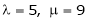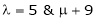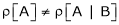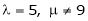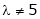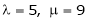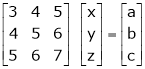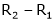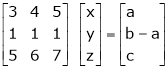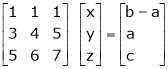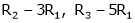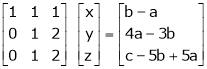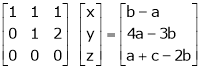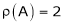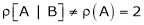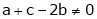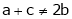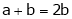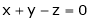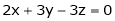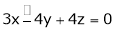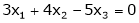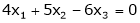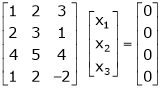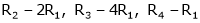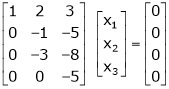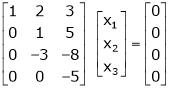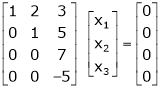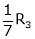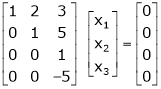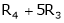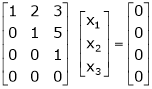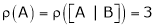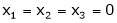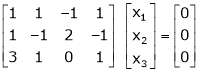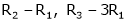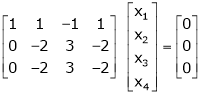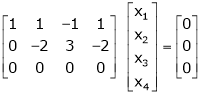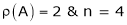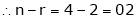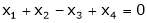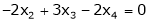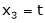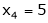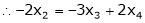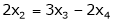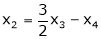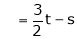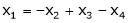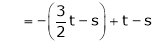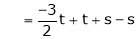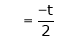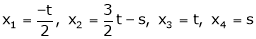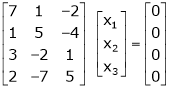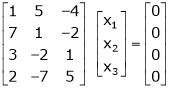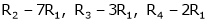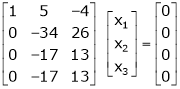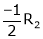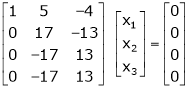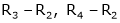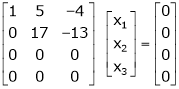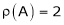UNIT 5
Linear Algebra-Matrices, System of Linear Equations
- Definition:
An arrangement of m.n numbers in m rows and n columns is called a matrix of order mxn.
Generally a matrix is denoted by capital letters. Like, A, B, C, ….. etc.
2. Types of matrices:- (Review)
- Row matrix
- Column matrix
- Square matrix
- Diagonal matrix
- Trace of a matrix
- Determinant of a square matrix
- Singular matrix
- Non – singular matrix
- Zero/ null matrix
- Unit/ Identity matrix
- Scaler matrix
- Transpose of a matrix
- Triangular matrices
Upper triangular and lower triangular matrices,
14. Conjugate of a matrix
15. Symmetric matrix
16. Skew – symmetric matrix
3. Operations on matrices:
- Equality of two matrices
- Multiplication of A by a scalar k.
- Addition and subtraction of two matrices
- Product of two matrices
- Inverse of a matrix
4. Elementary transformations
a) Elementary row transformation
These are three elementary transformations
- Interchanging any two rows (Rij)
- Multiplying all elements in ist row by a non – zero constant k is denoted by KRi
- Adding to the elements in ith row by the kth multiple of jth row is denoted by
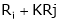 .
.
b) Elementary column transformations:
There are three elementary column transformations.
- Interchanging ith and jth column. is denoted by Cij.
- Multiplying ith column by a non – zero constant k is denoted by kCj.
- Adding to the element of ith column by the kth multiple of jth column is denoted by Ci + kCj.
Rank of a matrix:
Let A be a given rectangular matrix or square matrix. From this matrix select any r rows from these r rows select any r columns thus getting a square matrix of order r x r. The determinant of this matrix of order r x r is called minor or order r.
e.g. |
If |
For example select 2nd and 3rd row. i.e. |
|
Now select any two columns. Suppose, 1st and 2nd. |
i.e. |
Invariance of rank through elementary transformations.
- The rank of matrix remains unchanged by elementary transformations. i.e. from a matrix. A we get another matrix B by using some elementary transformation. Then
Rank of A = Rank of B
2. Equivalent matrices:
The matrix B is obtained from a matrix A by a sequence of a finite no. of elementary transformations is said to be equivalent to A. and we write.
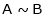
Normal form or canonical form:
Every mxn matrix of rank r can be reduced to the form 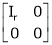
By a finite sequence of elementary transformation. This form is called normal form or the first canonical form of the matrix A.
Q1) Reduce the following matrix to normal form of Hence find it’s rank,
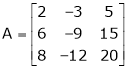
S1)
We have, |
|
|
|
|
|
Apply |
|
|
|
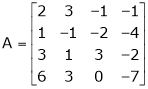
Q2) Find the rank of the matrix
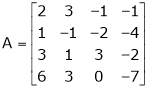
S2)
We have, |
|
Apply R12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q3) Find the rank of the following matrices by reducing it to the normal form.
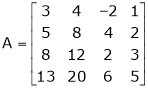
S3)
|
|
Apply C14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H.W.
Q4) Reduce the follo9wing matrices in to the normal form and hence find their ranks.
a) 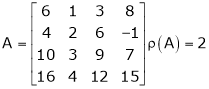
b) 
Q5) Reduction of a matrix a to normal form PAQ.
If A is a matrix of rank r, then there exist a non – singular matrices P & Q such that PAQ is in normal form.
i.e. 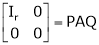
To obtained the matrices P and Q we use the following procedure.
Working rule:-
- If A is a mxn matrix, write A = Im A In.
- Apply row transformations on A on l.h.s. and the same row transformations on the prefactor Im.
- Apply column transformations on A on l.h.s and the column transformations on the postfactor In.
So that A on the l.h.s. reduces to normal form.
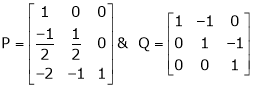
Ex1)
If 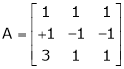 Find Two
Find Two
Matrices P and Q such that PAQ is in normal form.
S1)
Here A is a square matrix of order 3 x 3. Hence we write, |
A = I3 A.I3 |
i.e. |
|
|
|
|
|
|
|
|
|
|
i.e. |
|
|
|
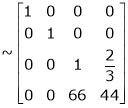
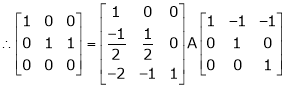
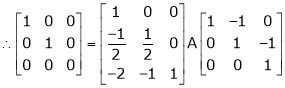
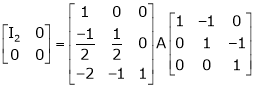
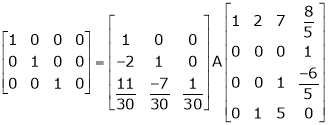
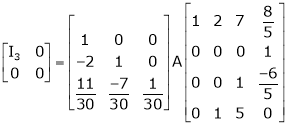
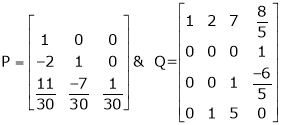
Ex2)
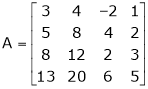
Find a non – singular matrices p and Q such that P A Q is in normal form where
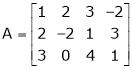
S2)
Here A is a matrix of order 3 x 4. Hence we write A as, |
|
i.e. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
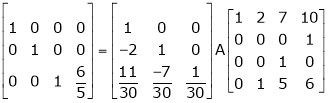
i.e. |
|
|
Simultaneous linear equations
- Non – homogeneous linear equations
Consider a system of m linear equations in n unknowns as,
|
|
Which can be written in matrix from as, |
Ax = B … (2) |
Where |
|
The matrix [A:B] or  formed by coefficient and constants is called augmented matrix.
formed by coefficient and constants is called augmented matrix.
Any set of values of the unknowns x1, x2, …..,xn which satisfied all the of the system AX = B.
When the system has at least one solution, then the system is said to be consistent, otherwise it is called inconsistent.
a) Condition of consistency:
1) If in a system of n linear equations and n unknown i.e. coefficient matrix of is of order n x n. (i.e. square matrix). & 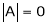 . i.e.
. i.e. 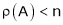 . Then the system has no solution.
. Then the system has no solution.
2) If coefficient matrix is of order mxn then
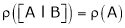 .
.
Then system is consistent.
b) Echelon form of a matrix:
A matrix is said to be echelon form if
1) There are some row which have all elements zero are placed at the bottom of the matrix.
2) The no. of zero elements in preceding row are less than the next row.
i.e. We have to make a given matrix. A to an upper triangular matrix by using a row transformations only.
c) Rank in echelon form
The rank of matrix is the no. of non – zero rows in echelon form of a matrix.
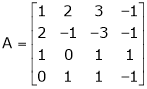
Ex 1) Reduce the following matrix to echelon form and find t rank.
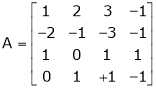
S1)
We have |
|
|
|
|
|
|
|
Which is the required row echelon form and no. of non – zero rows are. 2.
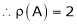
- Working rule to solve a system of non – homogeneous linear equations by reducing to echelon form.
a) Write the given system of m eqn. in n unknowns in matrix form as, AX = B.
b) Apply the row transformation on A as well as on the column matrix B. till you get an echelon from to A.
c) Then rewrite the equations as a set of linear equations.
d) We know that rank of a matrix in echelon form is equal to the no. of non – zero rows.
Case I
If rank (A) < Rank 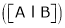 . Then equations are inconsistence i.e. they have no. solutions.
. Then equations are inconsistence i.e. they have no. solutions.
Case II
If rank A = Rank 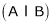 .
.
Then system has solution i.e. system is consistent. Further.
a) If r = n (i.e. rank of A is equal to no. of unknowns system has solution.
b) If 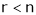 (i.e. rank of A is less than the no. of unknowns, system has infinitely many solutions.
(i.e. rank of A is less than the no. of unknowns, system has infinitely many solutions.
Ex.1)
Show that the equations
x + y = 1
2x + 3y = 1
5x – 7 = 11 are consistent and solve.
S1)
For consistency we have, Rank of A = Rank of [A l B] … (1) |
Now writing the given system in matrix form as, AX = B |
i.e. |
|
R2 – 2R1, R3 – 5R1 |
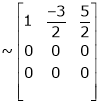
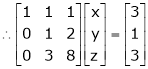
|
|
|
Thus Rank of A = 2 |
& Rank of [A | B] = 2 |
|
x + y = 1 |
y = -1 |
Solving them we get, |
y = -1, x=2 |
|
Ex. 2)
Solve system by matrix method
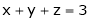
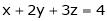
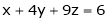
S2)
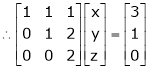
The given system can be written in matrix form as, |
Ax = B |
i.e. |
|
|
|
|
|
Here Rank of A = 23 |
& rank of [A | B] = 3 |
|
|
|
|
|
& |
& |
|
Thus the solution is x = 2, y = 1, z = 0 |
Ex. 3)
Test for consistency and solve by matrix method.
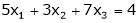
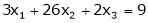
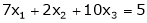
S3)
The given system ca be written in matrix form as, |
Ax = B |
i.e. |
|
|
|
|
|
|
|
|
|
|
|
Here Rank of A = 2 |
& Rank of [A | B] = 2 |
|
But r < n. (i.e. 2 < 3). |
Hence the system has infinitely many solutions. |
Now rewrite the equations are |
|
|
Put Z = t |
|
|
& |
|
|
Ex.4)
Test for consistency the following equations and if possible solve them by matrix method.
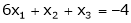
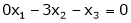
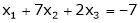
S4)
The given system can be written in matrix form as, Ax = B |
i.e. |
|
R13 |
|
|
|
|
|
|
|
|
|
Thus Rank of A = Rank of [A | B]. Hence the system is consistence now |
Rewriting the equations as, |
Z3 = 4 |
|
|
|
|
& |
|
|
|
|
Thus solution get is |
|
Ex. 5
For what value of ‘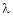 ’ the equations
’ the equations 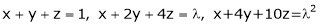 have a solution and solve them completely in each case.
have a solution and solve them completely in each case.
S5)
The given system can be written in matrix form as, |
Ax = B |
i.e. |
|
|
|
|
|
Since the system is consistent. |
|
|
|
|
|
Case I: |
If |
|
Rewriting equation as, |
|
|
Put |
& |
Case II: |
For |
|
Rewriting equation as, |
|
|
Put |
|
|
& |
|
|
Hence solution is |
|
Ex. 6)
For what value of 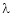 the equations
the equations
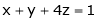
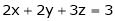
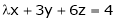
Will have no unique solution? Will the equations have any solution for this value of 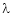 ?
?
S6)
The given system can be written in matrix form as, Ax = B. |
|
|
|
R12 |
|
The system has unique solutions if the coefficient matrix is non singular. |
i.e. |
|
|
|
Thus the above system has no unique solution for |
Now if |
|
|
|
|
|
Here |
Hence the system is inconsistent |
Ex.7)
Investigate for what values of 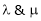 the equations
the equations
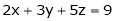
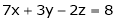
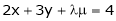 have
have
- No solution
- Unique solution
- An infinite no. of solutions?
S7)
The given system can be written in matrix form as, |
i.e. |
|
|
|
|
|
|
|
This system has unique solution if determinant of coefficient matrix is non – singular. |
i.e. |
|
Now if |
|
Now this system is consistent. |
If and only if |
|
|
Thus, if |
If |
|
Then system is inconsistent |
Thus |
|
2. A Unique solution if |
3. Infinitely many solutions if |
|
Ex.8)
Show that the system
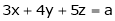
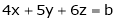
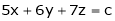 has no solution
has no solution
Unless 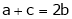
S8)
The given system can be written in matrix form as, Ax = 8 |
i.e. |
|
Apply |
|
R12 |
|
|
|
R3 – R2 |
|
Which is the required row echelon form, |
Here |
Thus the system has no solution |
If and only if |
i.e. |
If and only if |
i.e. |
hence the given system has no solution unless |
Solution: |
|
|
|
Solution: |
|
|
|
|
H.W.
Ex.8
Investigate for what values of 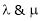 the equations,
the equations,
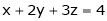
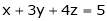
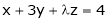
Have
- No solution
- A unique solution
- An infinite no. of solutions.
Homogeneous linear equations
If a system of linear equations every equations has r.h.s. is zero. Then this system is called homogeneous system of linear equation. Such a system can be written in matrix form as, AX = 0.
Where
A is the matrix of coefficient
X is the matrix of unknowns
O is the zero matrix (column)
Every homogeneous system has always a one solutions i.e. x1 = 0, x2 = 0, ….., xn=0. Such a solution is called as zero solute or trivial solution and all other solutions are called non–zero or non – trivial solutions (i.e. at least one of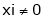 ).
).
Important result
Consider a homogeneous system of m linear equations in n unknowns, then the coefficient matrix. A will be mxn order let r be the rank of matrix A
Case I:
If r = n then system has a unique solution (i.e. 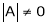
Case II:
If r < n; then the rank of matrix A is less than the no. of unknowns the system has infinitely many solutions i.e. non – trivial solution.
Ex. 1
Solve
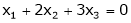
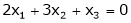
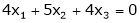
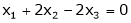
S1)
The given homogeneous system can be written matrix form as Ax = 0 |
i.e. |
|
|
|
-R2 |
|
|
|
|
|
|
|
Which is the required row echelon form. |
Here |
= no. of unknowns. |
Hence system has only trivial solution |
i.e. |
Ex. 2
Solve the equations
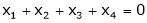
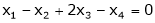
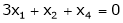
S2)
The given system can be written in matrix form as |
Ax = B |
i.e. |
|
|
|
|
|
Which is the required row echelon form. |
Here |
|
Now rewrite the equations as, |
|
|
Put |
|
|
|
|
|
|
|
|
|
Thus solution set is, |
|
Ex.3)
Some the following equations.
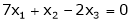
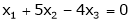
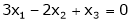
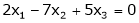
S3)
The given system can be written in matrix form as, Ax = 0 |
i.e. |
|
R12 |
|
|
|
|
|
|
|
Here |
i.e. r < n |
Hence system has infinity many solution and there are n – r = 3 – 2 = 1 independent variables. |
Reference Books:
1. Advanced Engineering Mathematics by Erwin Kreyszig (Wiley Eastern Ltd.)
2. Advanced Engineering Mathematics by M. D. Greenberg (Pearson Education)
3. Advanced Engineering Mathematics by Peter V. O’Neil (Thomson Learning)
4. Thomas’ Calculus by George B. Thomas, (Addison-Wesley, Pearson)
5. Applied Mathematics (Vol. I & Vol. II) by P.N.Wartikar and J.N.Wartikar Vidyarthi Griha Prakashan, Pune.
6. Linear Algebra –An Introduction, Ron Larson, David C. Falvo (Cenage Learning, Indian edition)