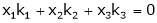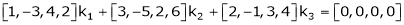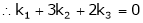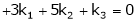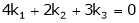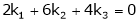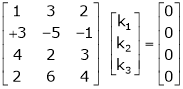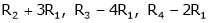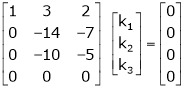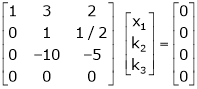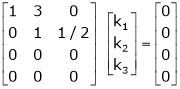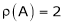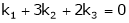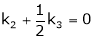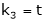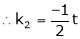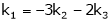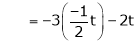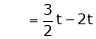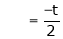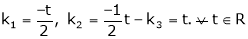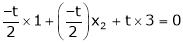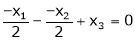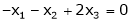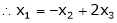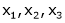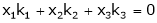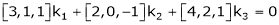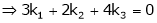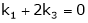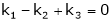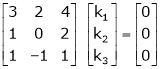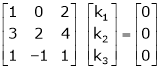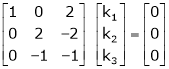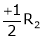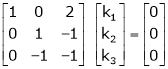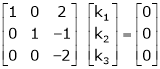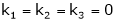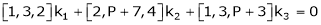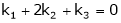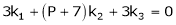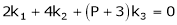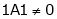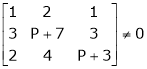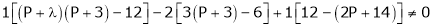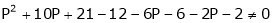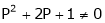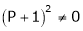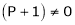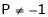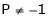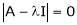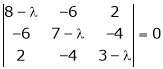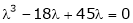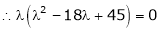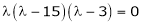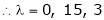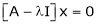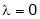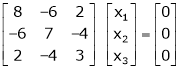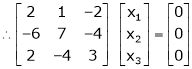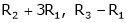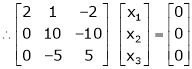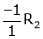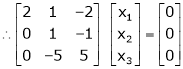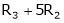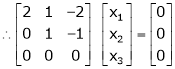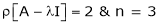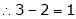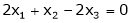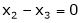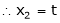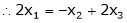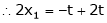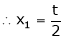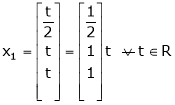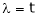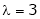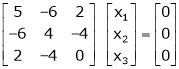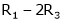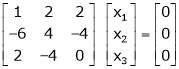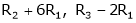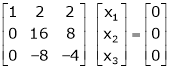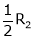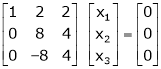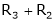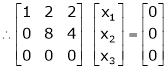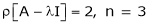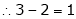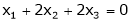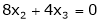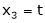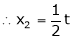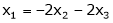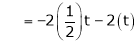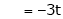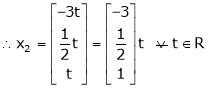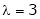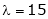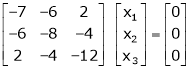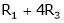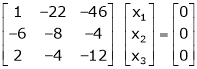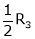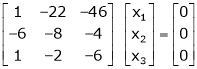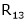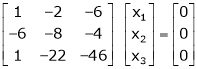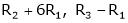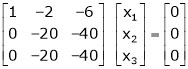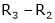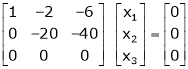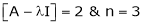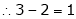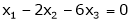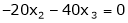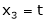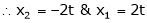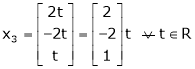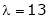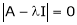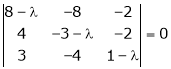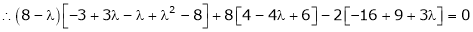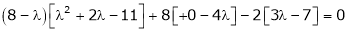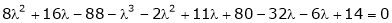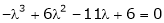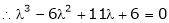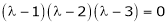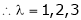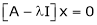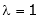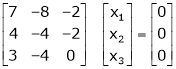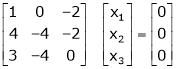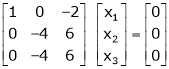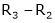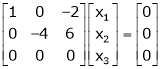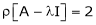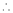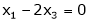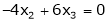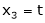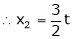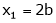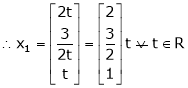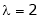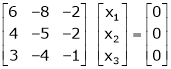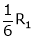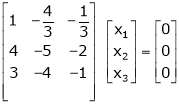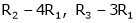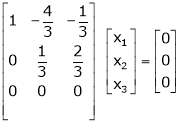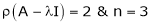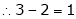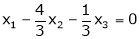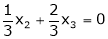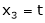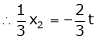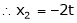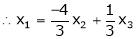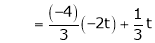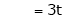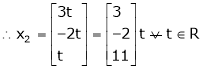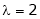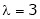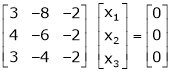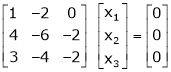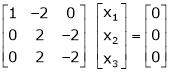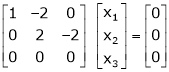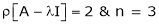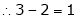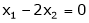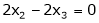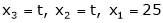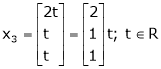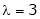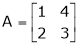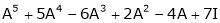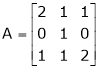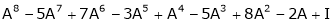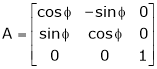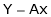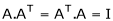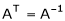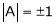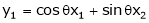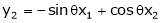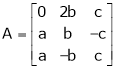6.1 Eigen Values and Eigen Vectors | unit 6 linear algebra eigen values and eigen vectors diagonaliztion

Chapter 6

Linear Algebra-Eigen Values and Eigen Vectors, Diagonaliztion

6.1 Eigen Values and Eigen Vectors

Introduction:

In this chapter we are going to study a very important theorem viz first we have to study of eigen values and eigen vector.

Vector

An ordered n – touple of numbers is called an n – vector. Thus the ‘n’ numbers x1, x2, ………… xn taken in order denote the vector x. i.e. x = (x1, x2, ……., xn).

Where the numbers x1, x2, ……….., xn are called component or co – ordinates of a vector x. A vector may be written as row vector or a column vector.

If A be an mxn matrix then each row will be an n – vector & each column will be an m – vector.

2. Linear Dependence

A set of n – vectors. x1, x2, …….., xr is said to be linearly dependent if there exist scalars. k1, k2, ……., kr not all zero such that

k1 + x2k2 + …………….. + xr kr = 0 … (1)

3. Linear Independence

A set of r vectors x1, x2, …………., xr is said to be linearly independent if there exist scalars k1, k2, …………, kr all zero such that

x1 k1 + x2 k2 + …….. + xr kr = 0

Note:-

Equation (1) is known as a vector equation.
If the vector equation has non – zero solution i.e. k1, k2, …., kr not all zero. Then the vector x1, x2, ………. xr are said to be linearly dependent.
If the vector equation has only trivial solution i.e.

k1 = k2 = …….= kr = 0. Then the vector x1, x2, ……, xr are said to linearly independent.

4. Linear combination

A vector x can be written in the form.

x = x1 k1 + x2 k2 + ……….+xr kr

where k1, k2, ………….., kr are scalars, then X is called linear combination of x1, x2, ……, xr.

Results:

A set of two or more vectors are said to be linearly dependent if at least one vector can be written as a linear combination of the other vectors.
A set of two or more vector are said to be linearly independent then no vector can be expressed as linear combination of the other vectors.

Ex1)

Are the vectors 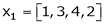, , 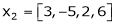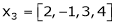linearly dependent. If so, express x1 as a linear combination of the others.

S1)

Consider a vector equation,

i.e.

Which can be written in matrix form as,

Here & no. of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,

Put

and

Thus

i.e.

Since F11 k2, k3 not all zero. Hence are linearly dependent.

Ex2)

Examine whether the following vectors are linearly independent or not.

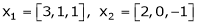and .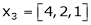

S2)

Consider the vector equation,

i.e. … (1)

Which can be written in matrix form as,

R12

R2 – 3R1, R3 – R1

R3 + R2

Here Rank of coefficient matrix is equal to the no. of unknowns. i.e. r = n = 3.

Hence the system has unique trivial solution.

i.e.

i.e. vector equation (1) has only trivial solution. Hence the given vectors x1, x2, x3 are linearly independent.

Ex3)

At what value of P the following vectors are linearly independent.

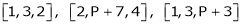
S3)

Consider the vector equation.

i.e.

Which is a homogeneous system of three equations in 3 unknowns and has a unique trivial solution.

If and only if Determinant of coefficient matrix is non zero.

consider .

i.e.

Thus for the system has only trivial solution and Hence the vectors are linearly independent.

Note:-

If the rank of the coefficient matrix is r, it contains r linearly independent variables & the remaining vectors (if any) can be expressed as linear combination of these vectors.

Characteristic equation:-

Let A he a square matrix, 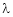be any scaler then 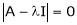is called characteristic equation of a matrix A.

Note:

Let a be a square matrix and ‘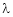’ be any scaler then,

1) 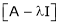is called characteristic matrix

2) 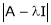is called characteristic polynomial.

The roots of a characteristic equations are known as characteristic root or latent roots, eigen values or proper values of a matrix A.

Eigen vector:-

Suppose 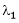be an eigen value of a matrix A. Then 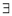a non – zero vector x1 such that.

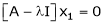… (1)

Such a vector ‘x1’ is called as eigen vector corresponding to the eigen value .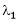

Properties of Eigen values:-

Then sum of the eigen values of a matrix A is equal to sum of the diagonal elements of a matrix A.
The product of all eigen values of a matrix A is equal to the value of the determinant.
If 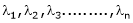are n eigen values of square matrix A then are m eigen values of a matrix A-1.
The eigen values of a symmetric matrix are all real.
If all eigen values are non – zen then A-1 exist and conversely.
The eigen values of A and A’ are same.

Properties of eigen vector:-

Eigen vector corresponding to distinct eigen values are linearly independent.
If two are more eigen values are identical then the corresponding eigen vectors may or may not be linearly independent.
The eigen vectors corresponding to distinct eigen values of a real symmetric matrix are orthogonal.

Ex1)

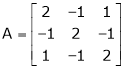
Determine the eigen values of eigen vector of the matrix.

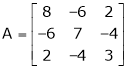
S1)

Consider the characteristic equation as,

i.e.

which is the required characteristic equation.

are the required eigen values.

Now consider the equation

… (1)

Case I:

If Equation (1) becomes

R1 + R2

Thus

independent variable.

Now rewrite equation as,

Put x3 = t

Thus .

Is the eigen vector corresponding to .

Case II:

If equation (1) becomes,

Here

independent variables

Now rewrite the equations as,

Put

Is the eigen vector corresponding to .

Case III:

If equation (1) becomes,

Here rank of

independent variable.

Now rewrite the equations as,

Put

Thus .

Is the eigen vector for .

Ex2)

Find the eigen values of eigen vector for the matrix.

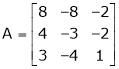
S2)

Consider the characteristic equation as

i.e.

are the required eigen values.

Now consider the equation

… (1)

Case I:

Equation (1) becomes,

Thus and n = 3

3 – 2 = 1 independent variables.

Now rewrite the equations as,

Put

i.e. the eigen vector for

Case II:

If equation (1) becomes,

Thus

Independent variables.

Now rewrite the equations as,

Put

Is the eigen vector for

Now

Case II:-

If equation (1) gives,

R1 – R2

Thus

independent variables

Now

Put

Thus

Is the eigen vector for .

6.2 Caylley Hamilton theorem

Every square matrix satisfied it’s characteristic equation

Ex.

Verify cayley – Hamilton theorem and use it to find A4 and A-1

Ex. Verify cayley – Hamilton theorem and hence find A-1, A-2, A-3

Ex. For find the value of , using cayley Hamilton theorem.

Ex. Find the characteristic equation of the matrix

And hence find the matrix represented by

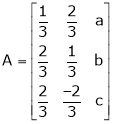
Verify whether the following matrix is orthogonal or not if so find A-1

6.3 Reduction of Quadratic forms to Canonical form by linear and orthogonal transformation

A linear transformation is said to orthogonal if it transforms .

The matrix of an orthogonal transfer motion is called on orthogonal matrix.

Definition:

A square matrix ‘A’ is said to be orthogonal if

Note:-

, for an orthogonal transformation
If ‘A’ is orthogonal then A-1, AT are also orthogonal.
If a is orthogonal,

Ex.

Show that the transformation

is orthogonal.

2. If is orthogonal, find a, b, c.

Ex. Determine the values of a, b, c when

is orthogonal.

Reference Books:

1. Advanced Engineering Mathematics by Erwin Kreyszig (Wiley Eastern Ltd.)

2. Advanced Engineering Mathematics by M. D. Greenberg (Pearson Education)

3. Advanced Engineering Mathematics by Peter V. O’Neil (Thomson Learning)

4. Thomas’ Calculus by George B. Thomas, (Addison-Wesley, Pearson)

5. Applied Mathematics (Vol. I & Vol. II) by P.N.Wartikar and J.N.Wartikar Vidyarthi Griha Prakashan, Pune.

6. Linear Algebra –An Introduction, Ron Larson, David C. Falvo (Cenage Learning, Indian edition)

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined