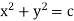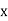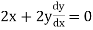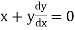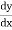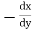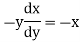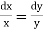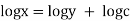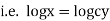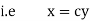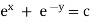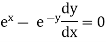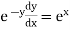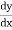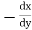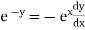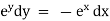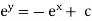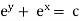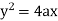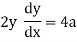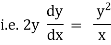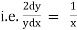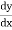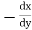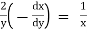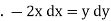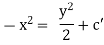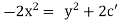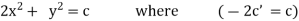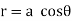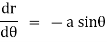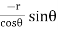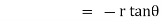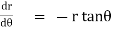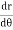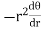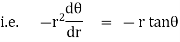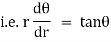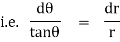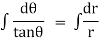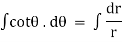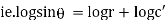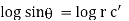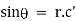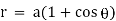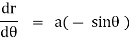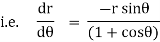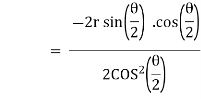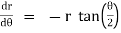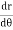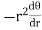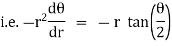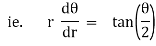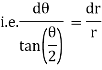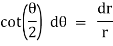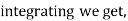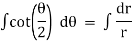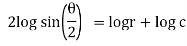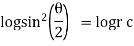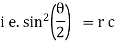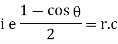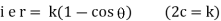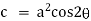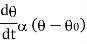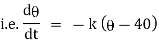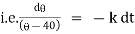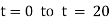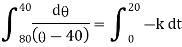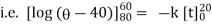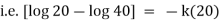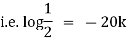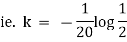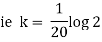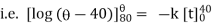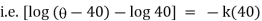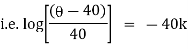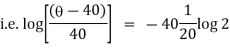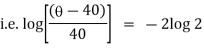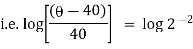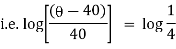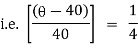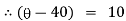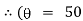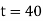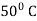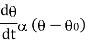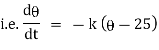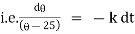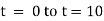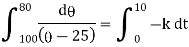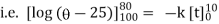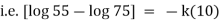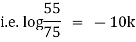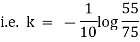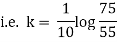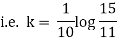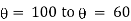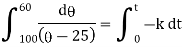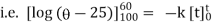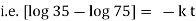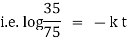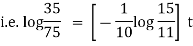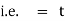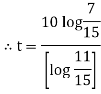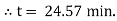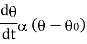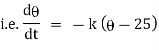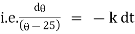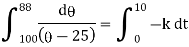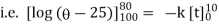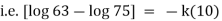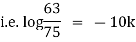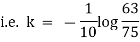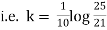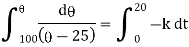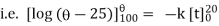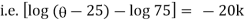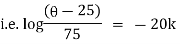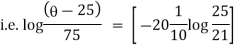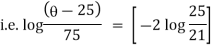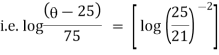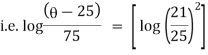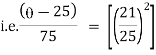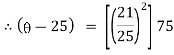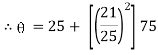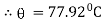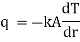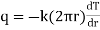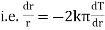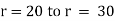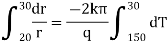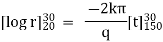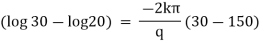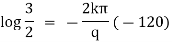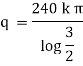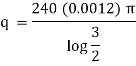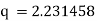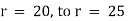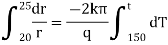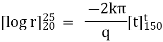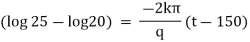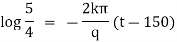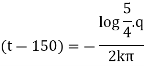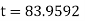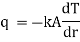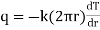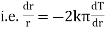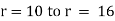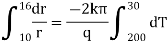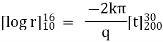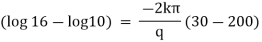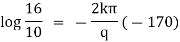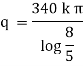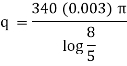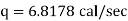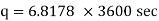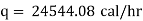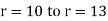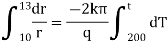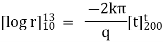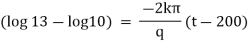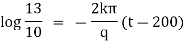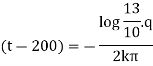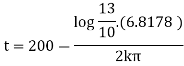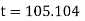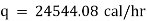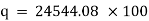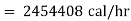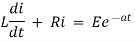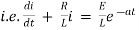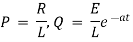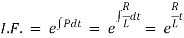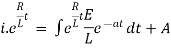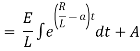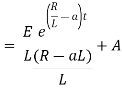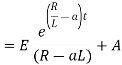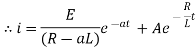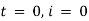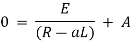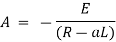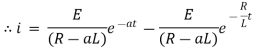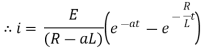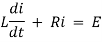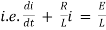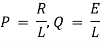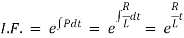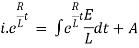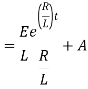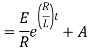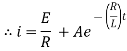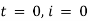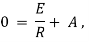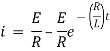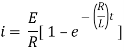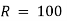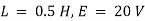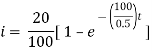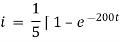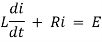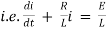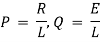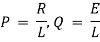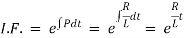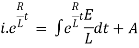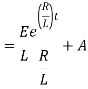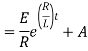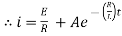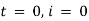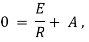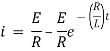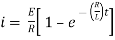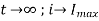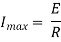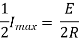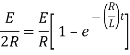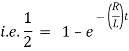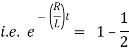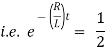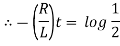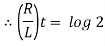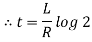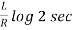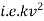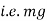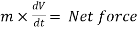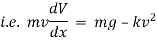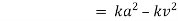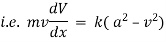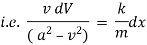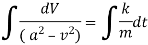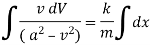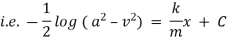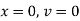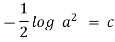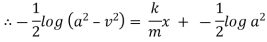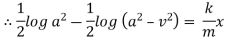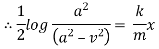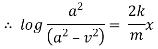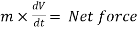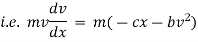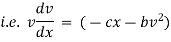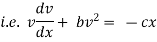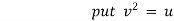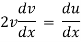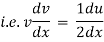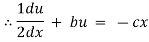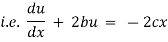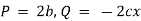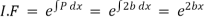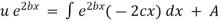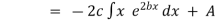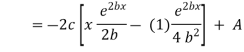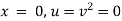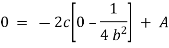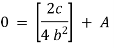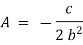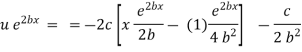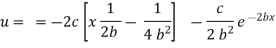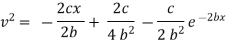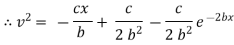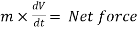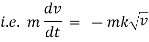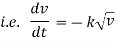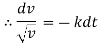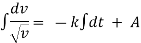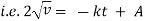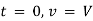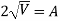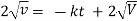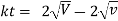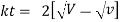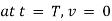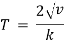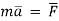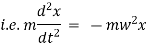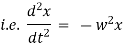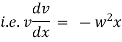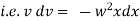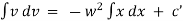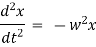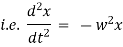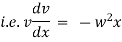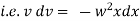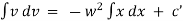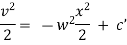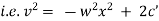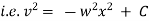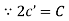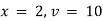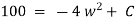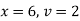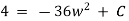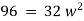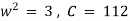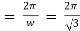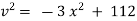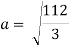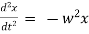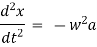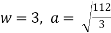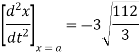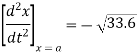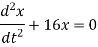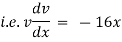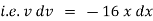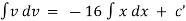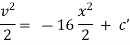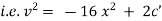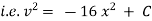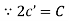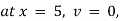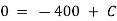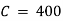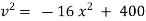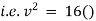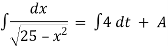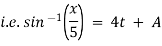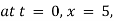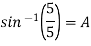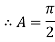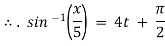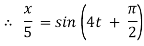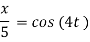UNIT –2
Application Of Differential Equation
Introduction :-
Differential equation plays a very important role in mathematics, physics and many branches of Engineering problems. In this chapter we will study some important problems in mechanical, Electrical Engineering.
There are some applications of differential equations in.
Orthogonal Trajectories :-
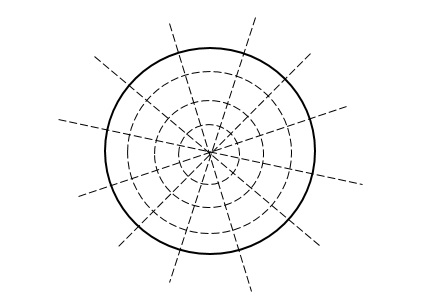
Two family of curves are said to be orthogonal trajectories if they cuts each member with every member of other family at right angles.
eg. A family of straight lines passing through origin i.e. y=mx and the family of circles . x2+y2=r2 ,are orthogonal trajectories
|
Working Rule to find orthogonal trajectories in Cartesian form (f(x,y)=c)
Consider the given function f(x,y,c)=0 Where c is arbitrary constant.
Step I :- Differential the given function
w.r.t x to find 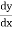 .
.
Step II :- Eliminate arbitrary constant, if any by using given equation.
Step III :- We have diff. equation of given family of curves.we Replace
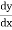 by
by 
Step V :- Solve the diff equation, we get the equation of orthogonal trajectory.
Note :- To find orthogonal trajectory in polar form f(r,) = c, we replace
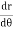 by
by 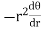
Proceeding as above we get orthogonal trajectory of given curves.
Ex) Find orthogonal trajectory of 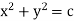
Sol)
|
We have, |
|
diff. w.r.t |
|
i.e. |
i.e |
which is a diff. equation of given family of curves. |
Now for orthogonal trajectories, replace |
|
|
i.e. |
integrating we get |
|
|
|
Which is the required orthogonal trajectories of given family of curves. |
Ex) Find the orthogonal trajectories of the family of 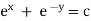
Sol)
We have, |
|
diff w.r.t |
|
|
i.e |
Which is a differential equation of given family of curves. |
To find orthogonal trajectories. We replace |
|
i.e. |
i.e. |
Integrating we get, |
i.e. |
i. e. |
Ex) Find the orthogonal trajectory of the family of 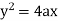
Sol)
We have, |
|
diff. w.r.t. x we get |
|
|
|
|
|
|
which is a diff equation of given family of curves. |
Now to find orthogonal trajectory |
we replace |
i.e. |
i.e |
integrating we get, |
|
i.e. |
i.e. |
is the required equation of given family of orthogonal trajectory. |
Exercise :-
Find orthogonal trajectories of
(i) 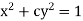
(ii) 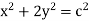
(iii) 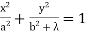 , where
, where 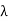 is a parameter
is a parameter
Ex) Find orthogonal trajectories of r = a cosθ.
Sol)
We have |
|
diff. w.r.t. we get, |
|
= |
|
Thus |
|
Which is a differential equation of given family of curves. To find orthogonal trajectory we replace |
|
|
|
|
|
|
|
|
|
|
|
It is the required equation of orthogonal trajectory. |
Ex) Find the orthogonal trajectories of family of curves.
r = a(1+cos ).
Sol)
We have, |
|
diff w.r.t . We get, |
|
|
|
|
|
|
|
|
Which is a differential equation of given family of curve? Now to find orthogonal trajectory we replace |
|
|
|
|
|
|
|
|
|
|
|
which is a required equation of orthogonal trajectory of given family of curves. |
Exercise :-
Find orthogonal trajectories of
2. 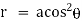
3. 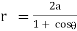
4. 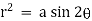
Newton’s low of cooling states that, the rate of temperature of the body is proportional to the difference between the temperature of the body and that of surrounding.
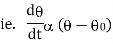
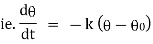
where
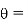 temperature of the body
temperature of the body
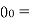 temperature of the surrounding
temperature of the surrounding
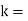 proportionality constant
proportionality constant
Ex) A body originally at 800 C cool to 600 C in 20 minutes, the temperature of air being 400 C, what will be the temperature of the body after 40 minutes from the original.
Sol)
Here |
= 800 C 0 = 400 C |
Now at t = 0 = 800 C |
t = 20 = 600 C |
t = 40 = ? |
Now by Newton’s cooling low |
|
|
integrating above from |
|
|
|
|
|
|
|
Now integrate above equation (1) from |
|
|
|
|
|
|
|
|
|
|
|
Thus at time |
Ex) A body at temperature 1000 C is placed in a room temperature whose temperature is 250 C and cools to 800 C in 10 minutes. Find the time when temperature will be 600 C.
Sol)
Here |
= 100 C 0 = 250 C |
Now at t = 0 = 1000 C |
t = 10 = 800 C |
t = ? = 600 C |
Now by Newton’s cooling low |
|
|
integrating equation (1) from |
|
|
|
|
|
|
|
|
|
Now integrating equation (1) from |
|
|
|
|
|
|
|
|
Ex) Water at temperature 1000 C cools in 10 minutes to 880 C in a room temperature 250 C. find the temperature of water after 20 minutes.
Sol)
Here |
= 1000 C 0 = 250 C |
Now at t = 0 = 1000 C |
t = 10 = 880 C |
t = 20 = ? |
Now by Newtons low of cooling, |
|
|
Now integrate equation 1 from t = 0 to t = 10 |
|
|
|
|
|
|
Now again integrate equation (1) from |
|
|
|
|
|
|
|
|
|
|
|
|
Thus at 20 minutes water will be at temperature 77.920 C |
Exercise :-
- The temperature of water initially is 1000 C and that of surrounding is 200 C. If the water will be the time required to fall temperature up to 300 C.
- If the temperature of air is 3000 C and the substance cools from 3700 C to 3400 C in 15 minutes. Find when the temperature will be 3100 C.
[C] Heat Flow (One Dimensional heat equation ):-
Whenever there is a temperature difference, there is heat transfer from warmer region to colder region (i.e. from high temperature region to low temperature region) by conduction mode of heat transfer.
Fourier low of Heat Conduction :-
Fourier low of heat conduction states that, the rate of heat conduction per unit area is directly proportional to the temperature gradient.
i.e. 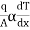
i.e. 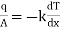
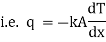
where q = rate of heat transfer.
K = Proportionality constant (Thermal Conductivity)
A = Area of heat transfer
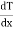 = Temperature gradient.
= Temperature gradient.
Note that for hallow pipe the Area = A = 2πx
[x = radius of circle]
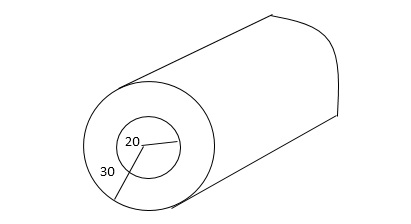
Ex) A steam pipe 40cm in diameter contains steam at 150 C and protected with covering 10cm thick for which k = 0.0012. If the temperature of the outer surface of covering is 30 C. Find the temperature at a distance 25cm from the centre of pipe under steady state conditions.
Sol)
|
Here at r1 = 20 t1 = 150 C, k = 0.0012 |
r2 = 30 t2 = 300 C |
and r = 25 t = ? |
Now by Fourier low of Heat Conduction, |
|
|
|
integrating equation (1) from |
|
|
|
|
|
|
|
|
Now again integrate equation (1) from |
We get, |
|
|
|
|
|
|
|
|
Thus |
Ex) A steam pipe 20cmin diameter is protected with a covering 6cm thick for which the co=efficient of thermal conductivity k = 0.003 cal/cm deg. Sec in steady state. Find the temperature half way through the covering if the covering is at 300 C. Also find the heat lost per hour through the meter length of a pipe.
Sol)
|
Here r1 =10 t1 =2000 C k = 0.003 |
r2 =16 t2 =300 C |
r =13 t = ? |
Now by Fourier low of heat flow, |
|
|
|
integrating equation (1) from |
|
|
|
|
|
|
|
|
|
|
Now again integrate equation (1) from |
|
|
|
|
|
|
|
|
Now heat lost per hour is |
|
Heat lost per hour through a 1 meter pipe is |
|
|
Exercise :-
- A pipe 10cm in diameter contains steam at 1000 C. It is covered with asbestos 5cm thick for which k = 0.0006 and outside surface is at 300 C. Find the amount of heat lost per hour from a meter long pipe.
2. A metallic pipe 20cm in diameter contains steam at 2000 C and is protected with covering 5cm thick for which k=0.025. If the temperature of outer surface is kept at 200 C. Find the temperature half way through the covering under steady condition. Also find quantity of heat loss if pipe is of 2 meter length.
[ D ] Simple Electric Circuit :-
Consider the circuit which contains
(i). Resistance(R) (ii).Inductance(L)
(iii). Capacitance(C) & (in Battery / Generator(E).
Symbols :-
(i). Resistance (R) :-
 (ii). Capacitance (C) :-
(ii). Capacitance (C) :-
 (iii). Inductance (L) :-
(iii). Inductance (L) :-
 (iv). Battery (E) :-
(iv). Battery (E) :-
 (v)Generator (E) :-
(v)Generator (E) :-
Basic Relations :-
(i).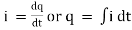
(ii). Now by ohms law
(a). Voltage drop across resistance 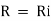
(b). Voltage drop across capacitance 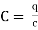
(c). Voltage drop across inductance 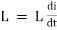
Kirchhoff’s Law :-
The algebraic sum of voltage drop around any closed circuit is equal to the resultant electromotive force in the circuit.
Some Useful Formulae :-
i) 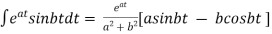
ii) 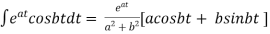
iii) 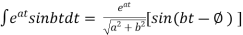
iv) 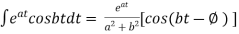
Where 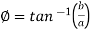
Ex) A voltage E e-at is applied at t = 0 to a circuit containing inductance L and resistance R, show that the current at any time t is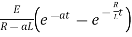
Sol)
By Kirchhoff’s law, |
|
|
Which is a linear differential equation with |
|
|
|
|
|
|
|
|
|
Now at |
|
|
|
|
Ex) A resistance 100 ohms, an inductance 0.5 H are connected in a series with battery of 20 V. Find current in a circuit as a function of t.
Sol)
By Kirchhoff’s law, |
|
|
Which is a linear differential equation with |
|
|
|
|
|
|
|
Now at |
|
|
|
|
Now at |
|
|
Ex) A constant electromotive force E volts is applied to a circuit containing a constant Resistance R ohms in a series and constant inductance L henries. If the initial current is zero. Show that the current builds up to half it’s theoretical maximum in [ L/R log 2 ]sec.
Sol)
By Kirchhoff’s law, |
|
|
Which is a linear differential equation with |
|
|
|
|
|
|
|
|
|
|
|
|
Now as |
|
Thus |
|
Therefore From equation (2), |
|
|
|
|
|
|
|
|
Thus the current builds up its half theoretical maximum in |
.Exercise
- An electric circuit contains an inductance of 5 henries, Resistance of 12 ohms in a series with an emf 120 sin20t volts. Find current at t = 0.01 if it is zero when t = 0
2. The equation of electromotive force in terms of current I, for an electric circuit having resistance R, and condencer of capacity C, in a series is E = R i + ∫i/c dt.
Find the current i at time t when E = E0sinwt
3. In a circuit inductance L = 640 H, Resistance R = 250 Ω and emf E = 500 volts. Find the time that elapses before it reches 90 % of its maximum value.
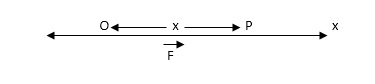
A motion of a particle or body along a straight line, is called rectilinear motion. The direction motion of a body is either upward or downward or slanting straight line.
Consider a body of mass ‘ m ’ starts moving from a fixed point ‘ O ’ along a straight line OX under the action of force F.
Let ‘P’ be the position of a body at any time ‘ t ’ where OP = x then,
(i). Velocity of a body is given by
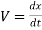
(ii). Acceleration of a body is given by,
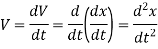
also
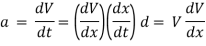
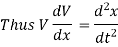
(iii). Momentum of a body = mass x Acceleration
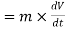
Newton’s second law of motion :-
The rate of change of momentum of a body is proportional to resultant force acting on a body.
Net force 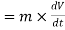
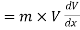 or
or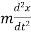
D’ Alembert Principle :-
The algebraic sum of forces acting on a body along a given direction is equal to the product of mass and acceleration in that direction.
Newton’s law of Gravitation :-
Every particle attracts every other particle in the universe with a force which is directly proportional to the product of the masses and inversely proportional to the square of the distance between their centres.
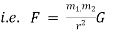 ( G is gravitational constant )
( G is gravitational constant )
Terminal velocity :-
Terminal velocity is the maximum velocity attainable by an object as it falls through a fluid or air.
Retarding Force :-
It is a force which produces negative acceleration on a body. It is a force which mainly resist motion & brings it to rest position. Thus retarding force brings retardation of a body and decreases its velocity
Ex. A body of mass ‘ m ’ falling from rest is subject to a force of gravity and an air resistance proportional to the square of velocity 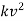 . If it falls through a distance
. If it falls through a distance 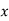 and passes a velocity
and passes a velocity 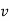 at that instant prove that
at that instant prove that 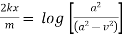
where 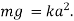
Sol)
Here the forces acting on a body are, |
(i). The resistance due to air |
(ii). The gravitational acceleration |
By Newton’s second law of motion. |
|
|
|
|
|
Integrating we get, |
|
|
|
|
Now initially at |
|
|
|
|
|
which is the required result. |
Ex) A moving body opposed by a force per unit mass of value cx and resistance per unit of mass of value bv2 where x and v are displacement and velocity of a particle of that instant. Find the velocity of the particle in terms of x if it starts from rest
Sol)
By Newton’s second law of motion |
|
|
|
|
|
|
|
|
|
|
which is a linear differential equation |
with |
|
Hence it’s solution is given by, |
|
|
|
Now at |
|
|
|
Thus |
|
|
|
|
which is the required velocity. |
Ex) A bullet is fired into sand tank, it’s retardation is proportional to square root of it’s velocity. Show that in time 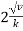 the bullet will come to rest.
the bullet will come to rest.
Where v is the initial velocity.
Sol)
By Newtons second law of motion, |
|
|
|
|
|
integrating we get, |
|
|
Now at |
|
|
|
|
|
Now |
|
is the required time. |
Exercise:-
1 A particle moves in a horizontal line OA with an acceleration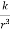 at a distance r and directed towards O. Initially a particle was at rest at a distance ‘ a ’ from O. Find the time when it will be at a distance
at a distance r and directed towards O. Initially a particle was at rest at a distance ‘ a ’ from O. Find the time when it will be at a distance from O.
from O.
2 The acceleration of moving particle being proportional to the cube of its velocity & negative, show that distance passed over in time t is given by
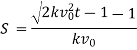
Where 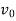 being initial velocity and the distance being measured from the position of particle at time
being initial velocity and the distance being measured from the position of particle at time 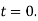
Simple Harmonic Motion :-
A particle is said to execute simple harmonic motion, if the particle moves in a straight line and the force acting on it is always directed towards a fixed point in the line and is proportional to the distance of the particle from the fixed point.
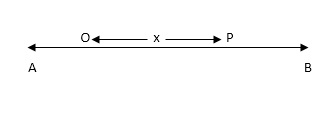 Let ‘P’ be the position of the particle at any time ‘t’ moving in the line AB and let O be the fixed point and OP = x as shown below,
Let ‘P’ be the position of the particle at any time ‘t’ moving in the line AB and let O be the fixed point and OP = x as shown below,
Equation of motion of particle is, |
|
|
|
|
|
integrating we get, |
|
Note :-
- Maximum displacement on either sde of ‘ O ’ is called as amplitude
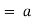 .
. - Frequency
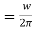
- S.H.M. is a periodic motion with period =
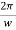
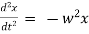 represents diff. equation of SHM
represents diff. equation of SHM- We have maximum acceleration when velocity
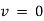
Ex) A particle execute SHM when it is 2cm from mid path it’s velocity is 10 cm/sec and when it is 6 cm from centre of it’s path it’s velocity is 2 cm/sec. Find his period &greatest acceleration.
Sol)
We have for S.H.M. |
|
|
|
|
integrating we get, |
|
|
integrating we get, |
|
|
|
Now when |
|
Also when |
|
Solving (1) & (2) we get, |
|
|
Thus period |
|
Now the greatest acceleration is achieved when |
|
|
|
|
Now Acceleration = |
|
But |
|
|
Thus gretest acceleration is |
Ex) The motion of a particle moving along a straight line is given by 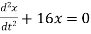 with initial conditions
with initial conditions 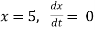 when
when 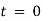 . Find the displacement at time t.
. Find the displacement at time t.
Sol)
We have, |
|
|
|
integrating we get, |
|
|
|
|
Now |
|
|
|
|
|
But |
|
|
integrating we get, |
|
|
now initially |
|
|
|
|
|
|
which is the required displacement at any time t. |
Exercise:-
1 A particle executing SHM has velocity 8 cm/sec and 6 cm/sec when it is at distance 3 cm & 4 cm respectively from the centre of its path find its period & amplitude.
2 A body moves in SHM accelerating to the low 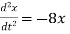 ; if
; if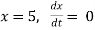 Find the period and amplitude.
Find the period and amplitude.
3 In case of starched elastic spring which has one end fixed and a particle of mass m attached at the other end. The equation of motion is,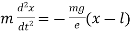 where
where 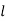 is natural length spring and
is natural length spring and 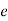 is the elongation due to weight
is the elongation due to weight 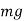 . find
. find 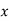 and
and 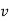 under the condition that at
under the condition that at 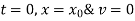
Reference Books:
1. Advanced Engineering Mathematics by Erwin Kreyszig (Wiley Eastern Ltd.)
2. Advanced Engineering Mathematics by M. D. Greenberg (Pearson Education)
3. Advanced Engineering Mathematics by Peter V. O’Neil (Thomson Learning)
4. Thomas’ Calculus by George B. Thomas, (Addison-Wesley, Pearson)
5. Applied Mathematics (Vol. I and II) by P.N. Wartikar and J.N.Wartikar Vidyarthi Griha Prakashan, Pune.
6. Differential Equations by S. L. Ross (John Wiley and Sons)