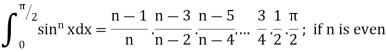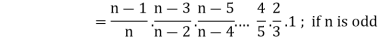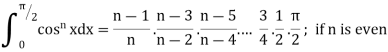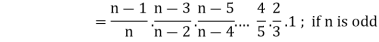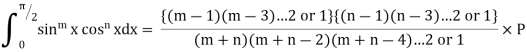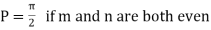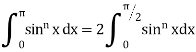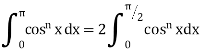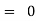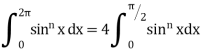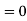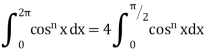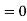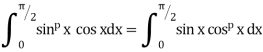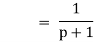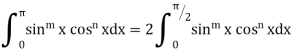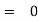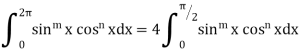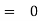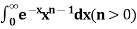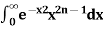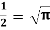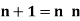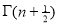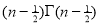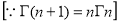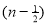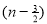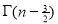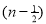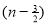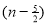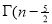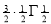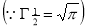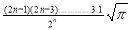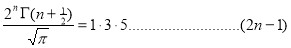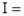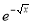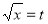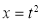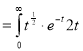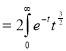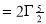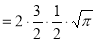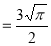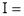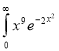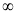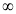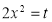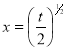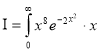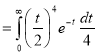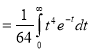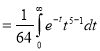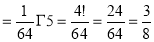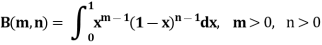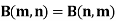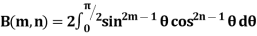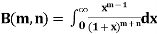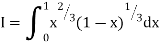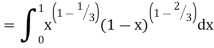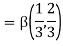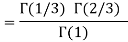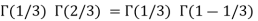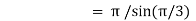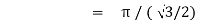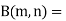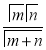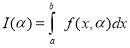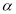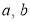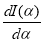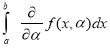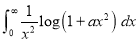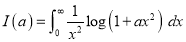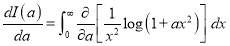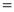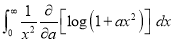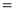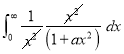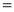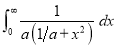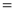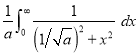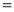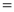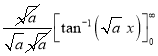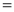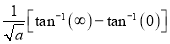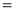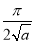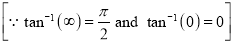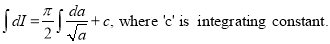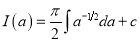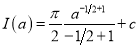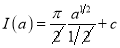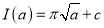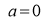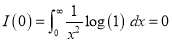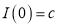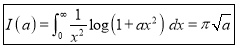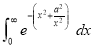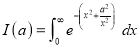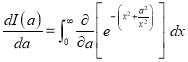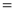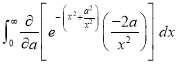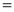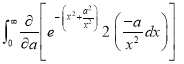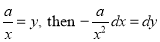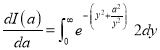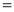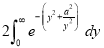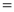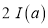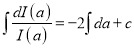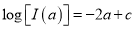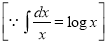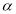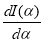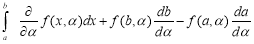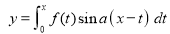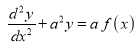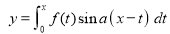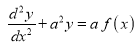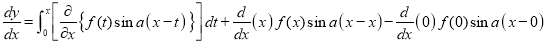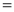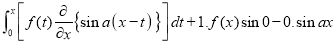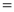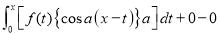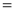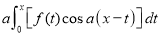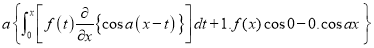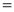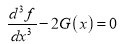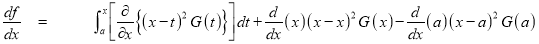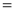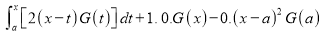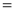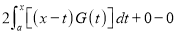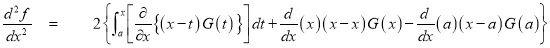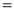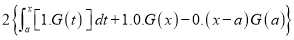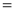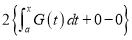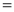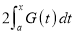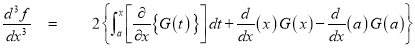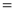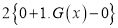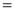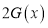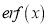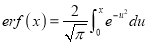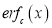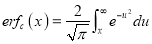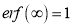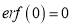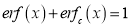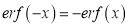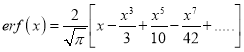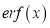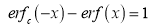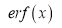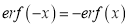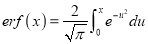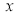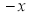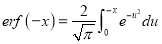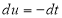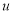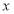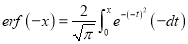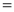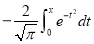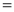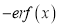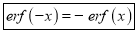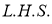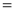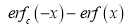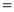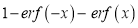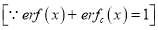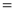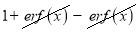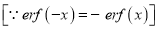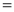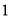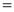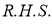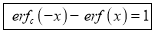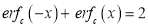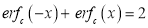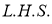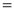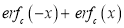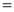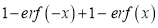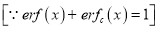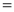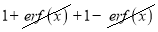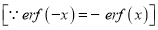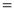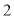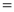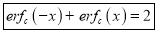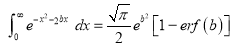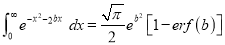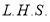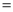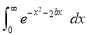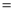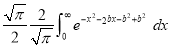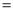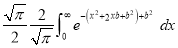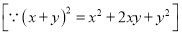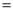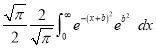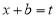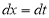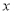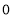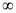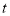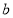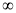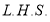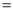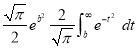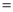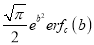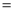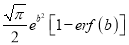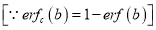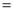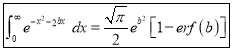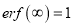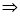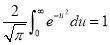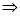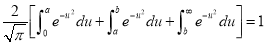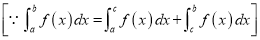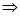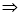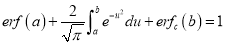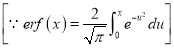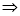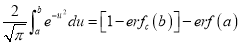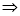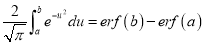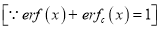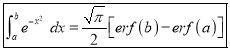3.1 REDUCTION FORMULAE | unit 3 integral calculus

Back to Study material

Unit-3

Integral Calculus

3.1 REDUCTION FORMULAE

Reduction formulae:

Where

Ex1) cos3 x dx

Sol)

Here n = 3, odd

cos3 x dx = 1

Ex2) cos8x dx

Sol)

Here n = 8 = even

cos8 x dx = 

Ex3) Evaluate cos3cos4 d

Sol)

By using reduction formula

sin3cos4  d =  1

Ex4) Evaluate sin6cos8 d

Sol)

= 

(∵ m and n both are even)

Ex5) Evaluate sin6cos5 d

Sol)

=  1

Ex6) Evaluate sin4 cos8 d

Sol)

= 

Ex7) (sin x )4 (cos x)2 dx

Sol)

We have,

f(x) dx = f(x) dx + f( – x) dx

 I = sin4 (x) (cos x)2 dx + [sin – (– x)]4 [cos (– x)]2 dx

= sin4 x cos2 x dx + sin4 x cos2 x dx

= +

= 2

 I =

REDUCTION FORMULAE PROBLEMS, GAMMA FUNCTION

Additional results :

For all integral values of n.

II.

If n is an even integer.

If n is an odd integer.

III.

If n is an even integer.

If n is an odd integer.

IV.

If n is an even integer.

If n is an odd integer.

VI.

If n is even, m is even or odd

If n is odd, m is even or odd

VII.

If m and n both are even

Otherwise

Ex1) dx

Sol)

Put x = sin  dx = cos d

When x = 0,  = 0

x = 1,  = /2

 I = cos d

= sin7  d

=  1

Ex2) dx

Sol)

Put x = sin  dx = cos d

 = 0 to /2

I = cos d

= 4 sin2 d – sin4 4 d

= 4 –

=  –

Ex3) dx

Sol)

Put x = 3 sin2 dx = 6 sin cos d

 = 0 to /2

I =  6 sin cos d

I = 6 sin cos d

= 18 sin4 a d

= 189

I =

Ex4) Find the reduction formula for sinn x dx and hence evaluate sin6 x dx

Sol)

Let In= sinn x dx

= sinn – 1 x sin x dx

Integrating by parts,

= sinn – 1 x  sin x dx –

= [sinn– 1 x (– cos x)] – [(n – 1) sinn – 2 x (cos x)] (– cos x) dx

= + (n – 1) sinn – 2 x cos2 x dx

= – + (n – 1) sinn – 2 x (1 – sin2 x) dx

= – + (n – 1)

In = – + (n – 1) [In – 2 – In]

In + (n – 1) In = – + (n – 1) In – 2

n In = – + (n – 1) In – 2

In = – – + In – 2 …(1)

Now, sin6 x dx = I6

 Put n = 6 in equation (1)

I6 = – + I4

I6 = – + I4 …(2)

Put n = 4 in equation (1)

I4 = – + I2

I4 = – + I2 …(3)

Put n = 2 in equation (1)

I2 = – + I0

I2 = – + I0 …(4)

But I0 = sin0 x dx = 1 dx =

 Equation (4)  I2 = –

I2 = –

Equation (3)  I4 = –

= –

I4 = –

Equation (2)  I6 = –

= –

I6 = –

 sin6 x dx = –

GAMMA FUNCTION AND ITS PROPERTIES.

Definition : Gamma function

n =

Properties :

1. n = 2

2. 1 = 1

3.2 GAMMA FUNCTION, BETA FUNCTION

Ex1) Evaluate 0∞ x3/2 e -x dx

Sol) 0

∞ x3/2 e -x dx = 0∞ x 5/2-1 e -x dx

= γ(5/2)

= γ(3/2+ 1)

= 3/2 γ(3/2 )

= 3/2 . ½ γ(½ )

= 3/2 . ½ .π

= ¾ π

Ex2) Find γ(-½)

Sol) (-½) + 1 = ½
γ(-1/2) = γ(-½ + 1) / (-½)

= - 2 γ(1/2 )

= - 2 π

Ex3) Show that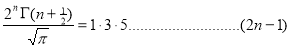

Sol)

= ) .......................

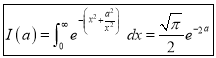
Ex4) Evaluate 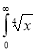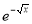dx.

Sol)

Let dx

X	0
t	0

Put or ;dx =2t dt .

Ex5) Evaluate 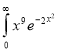dx.

Sol)

Let dx.

x	0
t	0

Put or ; 4x dx = dt

Definition : Beta function

Properties of Beta function :

Ex1) Evaluate I =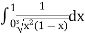

Sol)

= 2 π/3

Ex2) Evaluate: I = 02 x2 / (2 – x ) . dx

Sol)

Letting x = 2y, we get

I = (8/2) 01 y 2 (1 – y ) -1/2dy

= (8/2) . B(3 , 1/2 )

= 642 /15

BETA FUNCTION MORE PROBLEMS

Relation between Beta and Gamma functions :

Ex1) Evaluate: I = 0a x4  (a2 – x2 ) . dx

Sol)

Letting x2 = a2 y , we get

I = (a6 / 2) 01 y 3/2 (1 – y )1/2dy

= (a6 / 2) . B(5/2 , 3/2 )

= a6 /3 2

Ex2) Evaluate: I = 02 x (8 – x3 ) . dx

Sol)

Let x3 = 8y

I = (8/3) 01 y-1/3 (1 – y ) 1/3 . dy

= (8/3) B(2/3 , 4/3 )

= 16 π / ( 9 3 )

3.3 DIFFERENTIATION UNDER INTEGRAL SIGN RULE I (for one parameter)

RULE I: If where is parameter and are constants then

Q1) Evaluate:

(i) .

Sol)

Let

- - - - - - - - - - - - - - - - (1)

Differentiating by DUIS rule

Separating vectors and integrating, we have

- - - - - - - - - - - - - - - - (2)

Putting in equation (1) and (2), we get

and

(ii)

Solution:

Let

- - - - - - - - - - - - - - - - (1)

Differentiating by DUIS rule

Put

Integrating, we get

- - - - - - - - - - - - - - - - (2)

Putting in equation (1) and (2), we get

DIFFERENTIATION UNDER INTEGRAL SIGN RULE – II(Leibnitz’s Rule)

RULE II: Ifwhere are function of parameter then

Q)Prove that:

(i) If , then show that.

Sol)

We have given that

- - - - - - - - - - - - - - - - (1)

Then we have to prove that.

Differentiating by DUIS rule (Leibnitz’s Rule), we have

Again differentiating by DUIS rule (Leibnitz’s Rule), we have

This is the desired result.

(ii)If, then prove that.

Solution:

We have given that

- - - - - - - - - - - - - - - - (1)

Then we have to prove that.

Differentiating by DUIS rule (Leibnitz’s Rule), we have

Again differentiating by DUIS rule (Leibnitz’s Rule), we have

ERROR FUNCTION

Introduction to error function and its properties.

Error Function:

Error function is denoted by and defined as

2. Complementary Error function is denoted by and defined as

3. Properties of Error function

(i)

(ii)

(iii)

(iv) i.e. error function is odd function.

(v)

Q) Prove that

(i) is an odd function and hence deduce .

Sol)

We have to prove thatis an odd function i.e.

We know that

- - - - - - - - - - - - - - - - (1)

Replace by, we have

Put , then and

Hence the error function is odd function.

Now we have to prove that

Consider

This is the desired result.

(ii)

Solution:

We have to prove that

Consider

This is the desired result.

(iii)

Solution:

We have to prove that

Consider

Put , then and

This is the desired result.

(iv)

Solution:

We have to prove that

We know that

References:

Advanced Engineering Mathematics by Erwin Kreyszig (Wiley Eastern Ltd.)

2. Advanced Engineering Mathematics by M. D. Greenberg (Pearson Education)

3. Advanced Engineering Mathematics by Peter V. O’Neil (Thomson Learning)

4. Thomas’ Calculus by George B. Thomas, (Addison-Wesley, Pearson)

5. Applied Mathematics (Vol. I and II) by P.N. Wartikar and J.N.Wartikar Vidyarthi GrihaPrakashan, Pune.

6. Differential Equations by S. L. Ross (John Wiley and Sons)

Sign Up

Index

Notes

Highlighted

Underlined

Browse by Topics

Notes

Highlighted

Underlined