Unit 1
Introduction
Introduction
Data Structure can be defined as the group of data elements which provides an efficient way of storing and organising data in the computer so that it can be used efficiently. Some examples of Data Structures are arrays, Linked List, Stack, Queue, etc. Data Structures are widely used in almost every aspect of Computer Science i.e. Operating System, Compiler Design, Artifical intelligence, Graphics and many more.
Data Structures are the main part of many computer science algorithms as they enable the programmers to handle the data in an efficient way. It plays a vitle role in enhancing the performance of a software or a program as the main function of the software is to store and retrieve the user's data as fast as possible
Basic Terminology
Data structures are the building blocks of any program or the software. Choosing the appropriate data structure for a program is the most difficult task for a programmer. Following terminology is used as far as data structures are concerned
Data: Data can be defined as an elementary value or the collection of values, for example, student's name and its id are the data about the student.
Group Items: Data items which have subordinate data items are called Group item, for example, name of a student can have first name and the last name.
Record: Record can be defined as the collection of various data items, for example, if we talk about the student entity, then its name, address, course and marks can be grouped together to form the record for the student.
File: A File is a collection of various records of one type of entity, for example, if there are 60 employees in the class, then there will be 20 records in the related file where each record contains the data about each employee.
Attribute and Entity: An entity represents the class of certain objects. It contains various attributes. Each attribute represents the particular property of that entity.
Field: Field is a single elementary unit of information representing the attribute of an entity.
Need of Data Structures
As applications are getting complexed and amount of data is increasing day by day, there may arrise the following problems:
Processor speed: To handle very large amout of data, high speed processing is required, but as the data is growing day by day to the billions of files per entity, processor may fail to deal with that much amount of data.
Data Search: Consider an inventory size of 106 items in a store, If our application needs to search for a particular item, it needs to traverse 106 items every time, results in slowing down the search process.
Multiple requests: If thousands of users are searching the data simultaneously on a web server, then there are the chances that a very large server can be failed during that process
In order to solve the above problems, data structures are used. Data is organized to form a data structure in such a way that all items are not required to be searched and required data can be searched instantly.
Advantages of Data Structures
Efficiency: Efficiency of a program depends upon the choice of data structures. For example: suppose, we have some data and we need to perform the search for a perticular record. In that case, if we organize our data in an array, we will have to search sequentially element by element. Hence, using array may not be very efficient here. There are better data structures which can make the search process efficient like ordered array, binary search tree or hash tables.
Reusability: Data structures are reusable, i.e. once we have implemented a particular data structure, we can use it at any other place. Implementation of data structures can be compiled into libraries which can be used by different clients.
Abstraction: Data structure is specified by the ADT which provides a level of abstraction. The client program uses the data structure through interface only, without getting into the implementation details.
Data Structure Classification
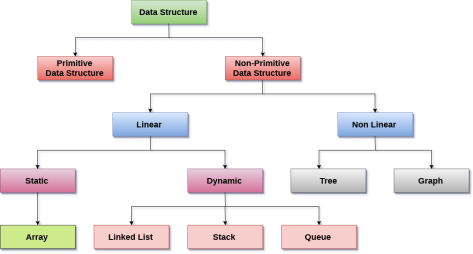
Linear Data Structures: A data structure is called linear if all of its elements are arranged in the linear order. In linear data structures, the elements are stored in non-hierarchical way where each element has the successors and predecessors except the first and last element.
Types of Linear Data Structures are given below:
Arrays: An array is a collection of similar type of data items and each data item is called an element of the array. The data type of the element may be any valid data type like char, int, float or double.
The elements of array share the same variable name but each one carries a different index number known as subscript. The array can be one dimensional, two dimensional or multidimensional.
The individual elements of the array age are:
Age[0], age[1], age[2], age[3],......... Age[98], age[99].
Linked List: Linked list is a linear data structure which is used to maintain a list in the memory. It can be seen as the collection of nodes stored at non-contiguous memory locations. Each node of the list contains a pointer to its adjacent node.
Stack: Stack is a linear list in which insertion and deletions are allowed only at one end, called top.
A stack is an abstract data type (ADT), can be implemented in most of the programming languages. It is named as stack because it behaves like a real-world stack, for example: - piles of plates or deck of cards etc.
Queue: Queue is a linear list in which elements can be inserted only at one end called rear and deleted only at the other end called front.
It is an abstract data structure, similar to stack. Queue is opened at both end therefore it follows First-In-First-Out (FIFO) methodology for storing the data items.
Non Linear Data Structures: This data structure does not form a sequence i.e. each item or element is connected with two or more other items in a non-linear arrangement. The data elements are not arranged in sequential structure.
Types of Non Linear Data Structures are given below:
Trees: Trees are multilevel data structures with a hierarchical relationship among its elements known as nodes. The bottommost nodes in the hierarchy are called leaf node while the topmost node is called root node. Each node contains pointers to point adjacent nodes.
Tree data structure is based on the parent-child relationship among the nodes. Each node in the tree can have more than one child except the leaf nodes whereas each node can have almost one parent except the root node. Trees can be classified into many categories which will be discussed later in this tutorial.
Graphs: Graphs can be defined as the pictorial representation of the set of elements (represented by vertices) connected by the links known as edges. A graph is different from tree in the sense that a graph can have cycle while the tree cannot have the one.
Operations on data structure
1) Traversing: Every data structure contains the set of data elements. Traversing the data structure means visiting each element of the data structure in order to perform some specific operation like searching or sorting.
Example: If we need to calculate the average of the marks obtained by a student in 6 different subjects, we need to traverse the complete array of marks and calculate the total sum, and then we will divide that sum by the number of subjects i.e. 6, in order to find the average.
2) Insertion: Insertion can be defined as the process of adding the elements to the data structure at any location.
If the size of data structure is n then we can only insert n-1 data elements into it.
3) Deletion: The process of removing an element from the data structure is called Deletion. We can delete an element from the data structure at any random location.
If we try to delete an element from an empty data structure then underflow occurs.
4) Searching: The process of finding the location of an element within the data structure is called Searching. There are two algorithms to perform searching, Linear Search and Binary Search. We will discuss each one of them later in this tutorial.
5) Sorting: The process of arranging the data structure in a specific order is known as Sorting. There are many algorithms that can be used to perform sorting, for example, insertion sort, selection sort, bubble sort, etc.
6) Merging: When two lists List A and List B of size M and N respectively, of similar type of elements, clubbed or joined to produce the third list, List C of size (M+N), then this process is called merging
Data Model is an abstract model that represents the data objects, data flow between these data objects, and the interrelationship between these data objects. It is a way of storing data on a computer so that it can be used in a more efficient manner for further purposes.
Data model or data structure consists of following fundamental elements:
1. Data object:
The data object is actually a location or region of storage that contains a collection of attributes or groups of values that act as an aspect, characteristic, quality, or descriptor of the object. A vehicle is a data object which can be defined or described with the help of a set of attributes or data.
Different data objects are present which are shown below:
- External entities such as a printer, user, speakers, keyboard, etc.
- Things such as reports, displays, signals.
- Occurrences or events such as alarm, telephone calls.
- Sales databases such as customers, store items, sales.
- Organizational units such as division, departments.
- Places such as manufacturing floor, workshops.
- Structures such as student records, accounts, files, documents.
2. Attributes:
Attributes define the properties of a data object. The attribute is a quality or characteristic that defines a person, group, or data objects. It is actually the properties that define the type of entity. An attribute can have a single or multiple or range of values as per our needs.
There are three types of attributes:
- Naming attributes –
To name an instance of a data object, naming attributes are used. User naming attributes identify user objects such as Login_names and User_Id for some security purpose. For example- Make and model are naming attributes in a vehicle data object. - Descriptive attributes –
These attributes are used to describe the characteristics or features or the relationship of the data object. Sometimes also referred to as relationship attributes. For example- In a vehicle, the color of a data object is a descriptive attribute that describes the features of the object. - Referential attribute –
These are the attributes that are used to formalize binary and associative relationships and in making reference to another instance in another table. For example- The data object is a referential attribute in a vehicle.
3. Relationship:
The relationship represents the connection or relation between different data objects and describes association among entities. Relationships are of three types: one-to-many, many-to-many, and many-to-one.
For example, toy and shopkeeper are two objects that share the following relationship:
- The Shopkeeper order toys.
- The shopkeeper sells toys.
- The shopkeeper shows toys.
- The Shopkeeper stocks toys.
What is Data Structure?
The data structure name indicates itself that organizing the data in memory. There are many ways of organizing the data in the memory as we have already seen one of the data structures, i.e., array in C language. Array is a collection of memory elements in which data is stored sequentially, i.e., one after another. In other words, we can say that array stores the elements in a continuous manner. This organization of data is done with the help of an array of data structures. There are also other ways to organize the data in memory. Let's see the different types of data structures.
The data structure is not any programming language like C, C++, java, etc. It is a set of algorithms that we can use in any programming language to structure the data in the memory.
To structure the data in memory, 'n' number of algorithms were proposed, and all these algorithms are known as Abstract data types. These abstract data types are the set of rules.
Types of Data Structures
There are two types of data structures:
- Primitive data structure
- Non-primitive data structure
Primitive Data structure
The primitive data structures are primitive data types. The int, char, float, double, and pointer are the primitive data structures that can hold a single value.
Non-Primitive Data structure
The non-primitive data structure is divided into two types:
- Linear data structure
- Non-linear data structure
Linear Data Structure
The arrangement of data in a sequential manner is known as a linear data structure. The data structures used for this purpose are Arrays, Linked list, Stacks, and Queues. In these data structures, one element is connected to only one another element in a linear form.
When one element is connected to the 'n' number of elements known as a non-linear data structure. The best example is trees and graphs. In this case, the elements are arranged in a random manner.
We will discuss the above data structures in brief in the coming topics. Now, we will see the common operations that we can perform on these data structures.
Data structures can also be classified as:
- Static data structure: It is a type of data structure where the size is allocated at the compile time. Therefore, the maximum size is fixed.
- Dynamic data structure: It is a type of data structure where the size is allocated at the run time. Therefore, the maximum size is flexible.
Major Operations
The major or the common operations that can be performed on the data structures are:
- Searching: We can search for any element in a data structure.
- Sorting: We can sort the elements of a data structure either in an ascending or descending order.
- Insertion: We can also insert the new element in a data structure.
- Updation: We can also update the element, i.e., we can replace the element with another element.
- Deletion: We can also perform the delete operation to remove the element from the data structure.
Which Data Structure?
A data structure is a way of organizing the data so that it can be used efficiently. Here, we have used the word efficiently, which in terms of both the space and time. For example, a stack is an ADT (Abstract data type) which uses either arrays or linked list data structure for the implementation. Therefore, we conclude that we require some data structure to implement a particular ADT.
An ADT tells what is to be done and data structure tells how it is to be done. In other words, we can say that ADT gives us the blueprint while data structure provides the implementation part. Now the question arises: how can one get to know which data structure to be used for a particular ADT?.
As the different data structures can be implemented in a particular ADT, but the different implementations are compared for time and space. For example, the Stack ADT can be implemented by both Arrays and linked list. Suppose the array is providing time efficiency while the linked list is providing space efficiency, so the one which is the best suited for the current user's requirements will be selected.
Advantages of Data structures
The following are the advantages of a data structure:
- Efficiency: If the choice of a data structure for implementing a particular ADT is proper, it makes the program very efficient in terms of time and space.
- Reusability: he data structures provide reusability means that multiple client programs can use the data structure.
- Abstraction: The data structure specified by an ADT also provides the level of abstraction. The client cannot see the internal working of the data structure, so it does not have to worry about the implementation part. The client can only see the interface.
- Primitive data structures
- Non-primitive data structures
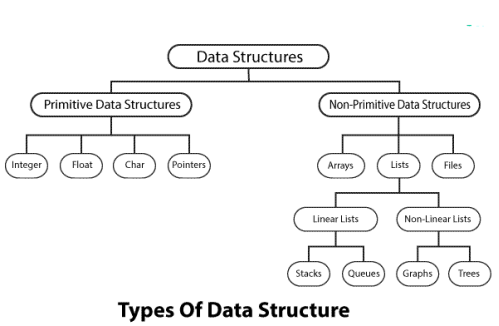
Primitive and Non-primitive data structures
Primitive Data Structures
Primitive Data Structures are the basic data structures that directly operate upon the machine instructions.
hey have different representations on different computers.
Integers, Floating point numbers, Character constants, String constants and Pointers come under this category.
Non-primitive Data Structures
Non-primitive data structures are more complicated data structures and are derived from primitive data structures.
They emphasize on grouping same or different data items with relationship between each data item.
Arrays, Lists and Files come under this category.
Linear Data Structures
A Linear data structure have data elements arranged in sequential manner and each member element is connected to its previous and next element. This connection helps to traverse a linear data structure in a single level and in single run. Such data structures are easy to implement as computer memory is also sequential. Examples of linear data structures are List, Queue, Stack, Array etc.
Non-linear Data Structures
A non-linear data structure has no set sequence of connecting all its elements and each element can have multiple paths to connect to other elements. Such data structures supports multi-level storage and often cannot be traversed in single run. Such data structures are not easy to implement but are more efficient in utilizing computer memory. Examples of non-linear data structures are Tree, BST, Graphs etc.
Following are the important differences between Linear Data Structures and Non-linear Data Structures.
Sr. No. | Key | Linear Data Structures | Non-linear Data Structures | |
1 | Data Element Arrangement | In linear data structure, data elements are sequentially connected and each element is traversable through a single run. | In non-linear data structure, data elements are hierarchically connected and are present at various levels. | |
2 | Levels | In linear data structure, all data elements are present at a single level. | In non-linear data structure, data elements are present at multiple levels. |
|
3 | Implementation complexity | Linear data structures are easier to implement. | Non-linear data structures are difficult to understand and implement as compared to linear data structures. |
|
4 | Traversal | Linear data structures can be traversed completely in a single run. | Non-linear data structures are not easy to traverse and needs multiple runs to be traversed completely. |
|
5 | Memory utilization | Linear data structures are not very memory friendly and are not utilizing memory efficiently. | Non-linear data structures uses memory very efficiently. |
|
6 | Time Complexity | Time complexity of linear data structure often increases with increase in size. | Time complexity of non-linear data structure often remain with increase in size. |
|
7 | Examples | Array, List, Queue, Stack. | Graph, Map, Tree. |
|
Data Structure is a way of storing and organising data efficiently such that the required operations on them can be performed be efficient with respect to time as well as memory. Simply, Data Structure are used to reduce complexity (mostly the time complexity) of the code.
Data structures can be two types :
1. Static Data Structure
2. Dynamic Data Structure
What is a Static Data structure?
In Static data structure the size of the structure is fixed. The content of the data structure can be modified but without changing the memory space allocated to it.
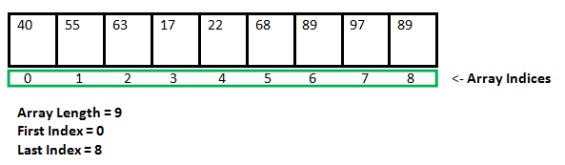
Example of Static Data Structures: Array
What is Dynamic Data Structure?
In Dynamic data structure the size of the structure in not fixed and can be modified during the operations performed on it. Dynamic data structures are designed to facilitate change of data structures in the run time.
Example of Dynamic Data Structures: Linked List
Static Data Structure vs Dynamic Data Structure
Static Data structure has fixed memory size whereas in Dynamic Data Structure, the size can be randomly updated during run time which may be considered efficient with respect to memory complexity of the code. Static Data Structure provides more easier access to elements with respect to dynamic data structure. Unlike static data structures, dynamic data structures are flexible.
Persistent data structures
All the data structures discussed here so far are non-persistent (or ephermal). A persistent data structure is a data structure that always preserves the previous version of itself when it is modified. They can be considered as ‘immutable’ as updates are not in-place.
A data structure is partially persistent if all versions can be accessed but only the newest version can be modified. Fully persistent if every version can be both accessed and modified. Confluently persistent is when we merge two or more versions to get a new version. This induces a DAG on the version graph.
Persistence can be achieved by simply copying, but this is inefficient in CPU and RAM usage as most operations will make only a small change is the DS. Therefore, a better method is to exploit the similarity between the new and old versions to share structure between them.
Examples:
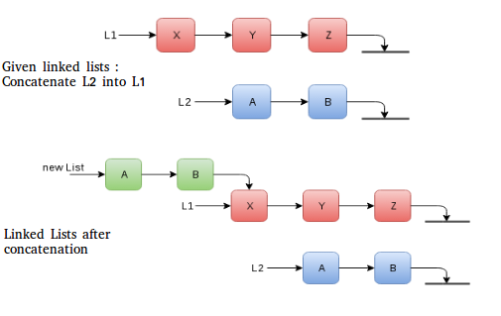
- Linked List Concatenation : Consider the problem of concatenating two singly linked lists with n and m as the number of nodes in them. Say n>m. We need to keep the versions, i.e., we should be able to original list.
One way is to make a copy of every node and do the connections. O(n + m) for traversal of lists and O(1) each for adding (n + m – 1) connections.
Other way, and a more efficient way in time and space, involves traversal of only one of the two lists and fewer new connections. Since we assume m<n, we can pick list with m nodes to be copied. This means O(m) for traversal and O(1) for each one of the (m) connections. We must copy it otherwise the original form of list wouldn’t have persisted.
2. Binary Search Tree Insertion: Consider the problem of insertion of a new node in a binary search tree. Being a binary search tree, there is a specific location where the new node will be placed. All the nodes in the path from the new node to the root of the BST will observe a change in structure (cascading). For example, the node for which the new node is the child will now have a new pointer. This change in structure induces change in the complete path up to the root. Consider tree below with value for node listed inside each one of them.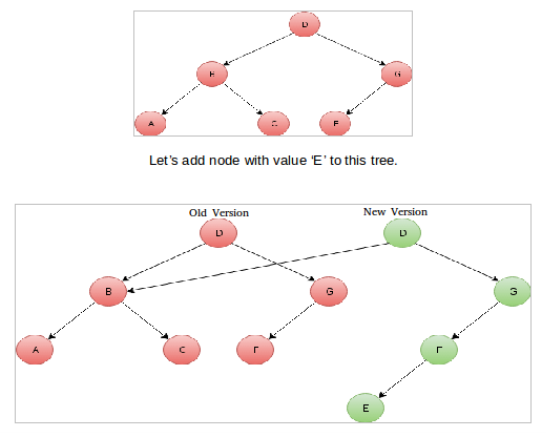
Approaches to make data structures persistent
For the methods suggested below, updates and access time and space of versions vary with whether we are implementing full or partial persistence.
- Path copying: Make a copy of the node we are about to update. Then proceed for update. And finally, cascade the change back through the data structure, something very similar to what we did in example two above. This causes a chain of updates, until you reach a node no other node points to — the root.
How to access the state at time t? Maintain an array of roots indexed by timestamp. - Fat nodes: As the name suggests, we make every node store its modification history, thereby making it ‘fat’.
- Nodes with boxes: Amortized O(1) time and space can be achieved for access and updates. This method was given by Sleator, Tarjan and their team. For a tree, it involves using a modification box that can hold:
a. One modification to the node (the modification could be of one of the pointers, or to the node’s key or to some other node-specific data)
b. The time when the mod was applied
The timestamp is crucial for reaching to the version of the node we care about. One can read more about it here.With this algorithm, given any time t, at most one modification box exists in the data structure with time t. Thus, a modification at time t splits the tree into three parts: one
part contains the data from before time t, one part contains the data from after time t, and
one part was unaffected by the modification.
Non-tree data structures may require more than one modification box, but limited to in-degree of the node for amortized O(1).
Ephemeral data
Much of the data stored on computers, such as the data stored in random access memory (RAM) and caches, is temporary and therefore referred to as "ephemeral" (which means transitory, or existing only briefly). These temporary, transient files are deleted as often as every few hours.
In computing, a "persistent data structure" is a data structure that always preserves the previous version of itself when it is modified. A data structure is partially persistent if all versions can be accessed but only the newest version can be modified. The data structure is fully persistent if every version can be both accessed and modified. If there is also a meld or merge operation that can create a new version from two previous versions, the data structure is called confluently persistent. Structures that are not persistent are called ephemeral.
The Data Type is basically a type of data that can be used in different computer program. It signifies the type like integer, float etc, the space like integer will take 4-bytes, character will take 1-byte of space etc.
The abstract datatype is special kind of datatype, whose behavior is defined by a set of values and set of operations. The keyword “Abstract” is used as we can use these datatypes, we can perform different operations. But how those operations are working that is totally hidden from the user. The ADT is made of with primitive datatypes, but operation logics are hidden.
Some examples of ADT are Stack, Queue, List etc.
Let us see some operations of those mentioned ADT −
- Stack −
- IsFull(), This is used to check whether stack is full or not
- IsEmpry(), This is used to check whether stack is empty or not
- Push(x), This is used to push x into the stack
- Pop(), This is used to delete one element from top of the stack
- Peek(), This is used to get the top most element of the stack
- Size(), this function is used to get number of elements present into the stack
- Queue −
- IsFull(), This is used to check whether queue is full or not
- IsEmpry(), This is used to check whether queue is empty or not
- Insert(x), This is used to add x into the queue at the rear end
- Delete(), This is used to delete one element from the front end of the queue
- Size(), this function is used to get number of elements present into the queue
- List −
- Size(), this function is used to get number of elements present into the list
- Insert(x), this function is used to insert one element into the list
- Remove(x), this function is used to remove given element from the list
- Get(i), this function is used to get element at position i
- Replace(x, y), this function is used to replace x with y value
Algorithm is a step-by-step procedure, which defines a set of instructions to be executed in a certain order to get the desired output. Algorithms are generally created independent of underlying languages, i.e. an algorithm can be implemented in more than one programming language.
From the data structure point of view, following are some important categories of algorithms −
- Search − Algorithm to search an item in a data structure.
- Sort − Algorithm to sort items in a certain order.
- Insert − Algorithm to insert item in a data structure.
- Update − Algorithm to update an existing item in a data structure.
- Delete − Algorithm to delete an existing item from a data structure.
Characteristics of an Algorithm
Not all procedures can be called an algorithm. An algorithm should have the following characteristics −
- Unambiguous − Algorithm should be clear and unambiguous. Each of its steps (or phases), and their inputs/outputs should be clear and must lead to only one meaning.
- Input − An algorithm should have 0 or more well-defined inputs.
- Output − An algorithm should have 1 or more well-defined outputs, and should match the desired output.
- Finiteness − Algorithms must terminate after a finite number of steps.
- Feasibility − Should be feasible with the available resources.
- Independent − An algorithm should have step-by-step directions, which should be independent of any programming code.
How to Write an Algorithm?
There are no well-defined standards for writing algorithms. Rather, it is problem and resource dependent. Algorithms are never written to support a particular programming code.
As we know that all programming languages share basic code constructs like loops (do, for, while), flow-control (if-else), etc. These common constructs can be used to write an algorithm.
We write algorithms in a step-by-step manner, but it is not always the case. Algorithm writing is a process and is executed after the problem domain is well-defined. That is, we should know the problem domain, for which we are designing a solution.
Example
Let's try to learn algorithm-writing by using an example.
Problem − Design an algorithm to add two numbers and display the result.
Step 1 − START
Step 2 − declare three integers a, b & c
Step 3 − define values of a & b
Step 4 − add values of a & b
Step 5 − store output of step 4 to c
Step 6 − print c
Step 7 − STOP
Algorithms tell the programmers how to code the program. Alternatively, the algorithm can be written as −
Step 1 − START ADD
Step 2 − get values of a & b
Step 3 − c ← a + b
Step 4 − display c
Step 5 − STOP
In design and analysis of algorithms, usually the second method is used to describe an algorithm. It makes it easy for the analyst to analyze the algorithm ignoring all unwanted definitions. He can observe what operations are being used and how the process is flowing.
Writing step numbers, is optional.
We design an algorithm to get a solution of a given problem. A problem can be solved in more than one ways.
Hence, many solution algorithms can be derived for a given problem. The next step is to analyse those proposed solution algorithms and implement the best suitable solution.
Algorithm Analysis
Efficiency of an algorithm can be analyzed at two different stages, before implementation and after implementation. They are the following −
- A Priori Analysis − This is a theoretical analysis of an algorithm. Efficiency of an algorithm is measured by assuming that all other factors, for example, processor speed, are constant and have no effect on the implementation.
- A Posterior Analysis − This is an empirical analysis of an algorithm. The selected algorithm is implemented using programming language. This is then executed on target computer machine. In this analysis, actual statistics like running time and space required, are collected.
We shall learn about a priori algorithm analysis. Algorithm analysis deals with the execution or running time of various operations involved. The running time of an operation can be defined as the number of computer instructions executed per operation.
Algorithm Complexity
Suppose X is an algorithm and n is the size of input data, the time and space used by the algorithm X are the two main factors, which decide the efficiency of X.
- Time Factor − Time is measured by counting the number of key operations such as comparisons in the sorting algorithm.
- Space Factor − Space is measured by counting the maximum memory space required by the algorithm.
The complexity of an algorithm f(n) gives the running time and/or the storage space required by the algorithm in terms of n as the size of input data.
Space Complexity
Space complexity of an algorithm represents the amount of memory space required by the algorithm in its life cycle. The space required by an algorithm is equal to the sum of the following two components −
- A fixed part that is a space required to store certain data and variables, that are independent of the size of the problem. For example, simple variables and constants used, program size, etc.
- A variable part is a space required by variables, whose size depends on the size of the problem. For example, dynamic memory allocation, recursion stack space, etc.
Space complexity S(P) of any algorithm P is S(P) = C + SP(I), where C is the fixed part and S(I) is the variable part of the algorithm, which depends on instance characteristic I. Following is a simple example that tries to explain the concept −
Algorithm: SUM(A, B)
Step 1 - START
Step 2 - C ← A + B + 10
Step 3 - Stop
Here we have three variables A, B, and C and one constant. Hence S(P) = 1 + 3. Now, space depends on data types of given variables and constant types and it will be multiplied accordingly.
Time Complexity
Time complexity of an algorithm represents the amount of time required by the algorithm to run to completion. Time requirements can be defined as a numerical function T(n), where T(n) can be measured as the number of steps, provided each step consumes constant time.
For example, addition of two n-bit integers takes n steps. Consequently, the total computational time is T(n) = c ∗ n, where c is the time taken for the addition of two bits. Here, we observe that T(n) grows linearly as the input size increases.
The main idea of asymptotic analysis is to have a measure of efficiency of algorithms that doesn’t depend on machine specific constants, and doesn’t require algorithms to be implemented and time taken by programs to be compared. Asymptotic notations are mathematical tools to represent time complexity of algorithms for asymptotic analysis. The following 3 asymptotic notations are mostly used to represent time complexity of algorithms.
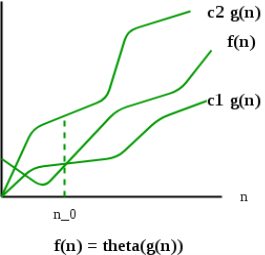
1) Θ Notation: The theta notation bounds a functions from above and below, so it defines exact asymptotic behavior.
A simple way to get Theta notation of an expression is to drop low order terms and ignore leading constants. For example, consider the following expression.
3n3 + 6n2 + 6000 = Θ(n3)
Dropping lower order terms is always fine because there will always be a n0 after which Θ(n3) has higher values than Θn2) irrespective of the constants involved.
For a given function g(n), we denote Θ(g(n)) is following set of functions.
Θ(g(n)) = {f(n): there exist positive constants c1, c2 and n0 such
That 0 <= c1*g(n) <= f(n) <= c2*g(n) for all n >= n0}
The above definition means, if f(n) is theta of g(n), then the value f(n) is always between c1*g(n) and c2*g(n) for large values of n (n >= n0). The definition of theta also requires that f(n) must be non-negative for values of n greater than n0.
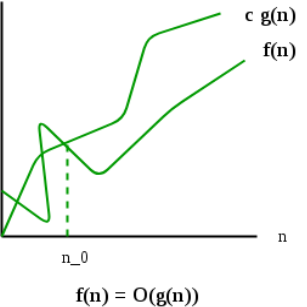
2) Big O Notation: The Big O notation defines an upper bound of an algorithm, it bounds a function only from above. For example, consider the case of Insertion Sort. It takes linear time in best case and quadratic time in worst case. We can safely say that the time complexity of Insertion sort is O(n^2). Note that O(n^2) also covers linear time.
If we use Θ notation to represent time complexity of Insertion sort, we have to use two statements for best and worst cases:
1. The worst case time complexity of Insertion Sort is Θ(n^2).
2. The best case time complexity of Insertion Sort is Θ(n).
The Big O notation is useful when we only have upper bound on time complexity of an algorithm. Many times we easily find an upper bound by simply looking at the algorithm.
O(g(n)) = { f(n): there exist positive constants c and
n0 such that 0 <= f(n) <= c*g(n) for
All n >= n0}
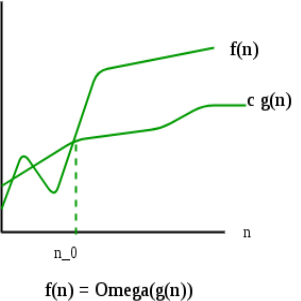
3) Ω Notation: Just as Big O notation provides an asymptotic upper bound on a function, Ω notation provides an asymptotic lower bound.
Ω Notation can be useful when we have lower bound on time complexity of an algorithm. As discussed in the previous post, the best case performance of an algorithm is generally not useful, the Omega notation is the least used notation among all three.
For a given function g(n), we denote by Ω(g(n)) the set of functions.
Ω (g(n)) = {f(n): there exist positive constants c and
n0 such that 0 <= c*g(n) <= f(n) for
All n >= n0}.
Let us consider the same Insertion sort example here. The time complexity of Insertion Sort can be written as Ω(n), but it is not a very useful information about insertion sort, as we are generally interested in worst case and sometimes in average case.
Properties of Asymptotic Notations :
As we have gone through the definition of this three notations let’s now discuss some important properties of those notations.
- General Properties :
If f(n) is O(g(n)) then a*f(n) is also O(g(n)) ; where a is a constant.
Example: f(n) = 2n²+5 is O(n²)
then 7*f(n) = 7(2n²+5)
= 14n²+35 is also O(n²)
Similarly this property satisfies for both Θ and Ω notation.
We can say
If f(n) is Θ(g(n)) then a*f(n) is also Θ(g(n)) ; where a is a constant.
If f(n) is Ω (g(n)) then a*f(n) is also Ω (g(n)) ; where a is a constant.
2. Reflexive Properties :
If f(n) is given then f(n) is O(f(n)).
Example: f(n) = n² ; O(n²) i.e O(f(n))
Similarly this property satisfies for both Θ and Ω notation.
We can say
If f(n) is given then f(n) is Θ(f(n)).
If f(n) is given then f(n) is Ω (f(n)).
3. Transitive Properties :
If f(n) is O(g(n)) and g(n) is O(h(n)) then f(n) = O(h(n)) .
Example: if f(n) = n , g(n) = n² and h(n)=n³
n is O(n²) and n² is O(n³)
then n is O(n³)
Similarly this property satisfies for both Θ and Ω notation.
We can say
If f(n) is Θ(g(n)) and g(n) is Θ(h(n)) then f(n) = Θ(h(n)) .
If f(n) is Ω (g(n)) and g(n) is Ω (h(n)) then f(n) = Ω (h(n))
4. Symmetric Properties :
If f(n) is Θ(g(n)) then g(n) is Θ(f(n)) .
Example: f(n) = n² and g(n) = n²
then f(n) = Θ(n²) and g(n) = Θ(n²)
This property only satisfies for Θ notation.
5. Transpose Symmetric Properties :
If f(n) is O(g(n)) then g(n) is Ω (f(n)).
Example: f(n) = n , g(n) = n²
then n is O(n²) and n² is Ω (n)
This property only satisfies for O and Ω notations.
6. Some More Properties :
- If f(n) = O(g(n)) and f(n) = Ω(g(n)) then f(n) = Θ(g(n))
- If f(n) = O(g(n)) and d(n)=O(e(n))
then f(n) + d(n) = O( max( g(n), e(n) ))
Example: f(n) = n i.e O(n)
d(n) = n² i.e O(n²)
then f(n) + d(n) = n + n² i.e O(n²) - If f(n)=O(g(n)) and d(n)=O(e(n))
then f(n) * d(n) = O( g(n) * e(n) )
Example: f(n) = n i.e O(n)
d(n) = n² i.e O(n²)
then f(n) * d(n) = n * n² = n³ i.e O(n³)
One dimensional Array
The variable allows us to store a single value at a time, what if we want to store roll no. Of 100 students? For this task, we have to declare 100 variables, then assign values to each of them. What if there are 10000 students or more? As you can see declaring that many variables for a single entity (i.e student) is not a good idea. In a situation like these arrays provide a better way to store data.
What is an Array?
An array is a collection of one or more values of the same type. Each value is called an element of the array. The elements of the array share the same variable name but each element has its own unique index number (also known as a subscript). An array can be of any type, For example: int, float, char etc. If an array is of type int then it's elements must be of type int only.
To store roll no. Of 100 students, we have to declare an array of size 100 i.e roll_no[100]. Here size of the array is 100 , so it is capable of storing 100 values. In C, index or subscript starts from 0, so roll_no[0] is the first element, roll_no[1] is the second element and so on. Note that the last element of the array will be at roll_no[99] not at roll_no[100] because the index starts at 0.
Arrays can be single or multidimensional. The number of subscript or index determines the dimensions of the array. An array of one dimension is known as a one-dimensional array or 1-D array, while an array of two dimensions is known as a two-dimensional array or 2-D array.
Let's start with a one-dimensional array.
One-dimensional array
Conceptually you can think of a one-dimensional array as a row, where elements are stored one after another.

Syntax: datatype array_name[size];
Datatype: It denotes the type of the elements in the array.
Array_name: Name of the array. It must be a valid identifier.
Size: Number of elements an array can hold. Here are some example of array declarations:
1 2 3 | Int num[100]; Float temp[20]; Char ch[50]; |
Num is an array of type int, which can only store 100 elements of type int.
temp is an array of type float, which can only store 20 elements of type float.
ch is an array of type char, which can only store 50 elements of type char.
Note: When an array is declared it contains garbage values.
The individual elements in the array:
1 2 3 | Num[0], num[1], num[2], ....., num[99] Temp[0], temp[1], temp[2], ....., temp[19] Ch[0], ch[1], ch[2], ....., ch[49] |
We can also use variables and symbolic constants to specify the size of the array.
1 2 3 4 5 6 7 8 9 10 | #define SIZE 10
Int main() { Int size = 10;
Int my_arr1[SIZE]; // ok Int my_arr2[size]; // not allowed until C99 // ... } |
Note: Until C99 standard, we were not allowed to use variables to specify the size of the array. If you are using a compiler which supports C99 standard, the above code would compile successfully. However, If you're using an older version of C compiler like Turbo C++, then you will get an error.
The use of symbolic constants makes the program maintainable, because later if you want to change the size of the array you need to modify it at once place only i.e in the #define directive.
Accessing elements of an array
The elements of an array can be accessed by specifying array name followed by subscript or index inside square brackets (i.e []). Array subscript or index starts at 0. If the size of an array is 10 then the first element is at index 0, while the last element is at index 9. The first valid subscript (i.e 0) is known as the lower bound, while last valid subscript is known as the upper bound.
Int my_arr[5];
Then elements of this array are;
First element – my_arr[0]
Second element – my_arr[1]
Third element – my_arr[2]
Fourth element – my_arr[3]
Fifth element – my_arr[4]
Array subscript or index can be any expression that yields an integer value. For example:
1 2 3 4 | Int i = 0, j = 2; My_arr[i]; // 1st element My_arr[i+1]; // 2nd element My_arr[i+j]; // 3rd element |
In the array my_arr, the last element is at my_arr[4], What if you try to access elements beyond the last valid index of the array?
1 2 3 | Printf("%d", my_arr[5]); // 6th element Printf("%d", my_arr[10]); // 11th element Printf("%d", my_arr[-1]); // element just before 0 |
Sure indexes 5, 10 and -1 are not valid but C compiler will not show any error message instead some garbage value will be printed. The C language doesn't check bounds of the array. It is the responsibility of the programmer to check array bounds whenever required.
Processing 1-D arrays
The following program uses for loop to take input and print elements of a 1-D array.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | #include<stdio.h>
Int main() { Int arr[5], i;
For(i = 0; i < 5; i++) { Printf("Enter a[%d]: ", i); Scanf("%d", &arr[i]); }
Printf("\nPrinting elements of the array: \n\n");
For(i = 0; i < 5; i++) { Printf("%d ", arr[i]); }
// signal to operating system program ran fine Return 0; } |
Expected Output:
1 2 3 4 5 6 7 8 9 | Enter a[0]: 11 Enter a[1]: 22 Enter a[2]: 34 Enter a[3]: 4 Enter a[4]: 34
Printing elements of the array:
11 22 34 4 34 |
How it works:
In Line 5, we have declared an array of 5 integers and variable i of type int. Then a for loop is used to enter five elements into an array. In scanf() we have used & operator (also known as the address of operator) on element arr[i] of an array, just like we had done with variables of type int, float, char etc. Line 13 prints "Printing elements of the array" to the console. The second for loop prints all the elements of an array one by one.
The following program prints the sum of elements of an array.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | #include<stdio.h>
Int main() { Int arr[5], i, s = 0;
For(i = 0; i < 5; i++) { Printf("Enter a[%d]: ", i); Scanf("%d", &arr[i]); }
For(i = 0; i < 5; i++) { s += arr[i]; }
Printf("\nSum of elements = %d ", s);
// signal to operating system program ran fine Return 0; } |
Expected Output:
1 2 3 4 5 6 7 | Enter a[0]: 22 Enter a[1]: 33 Enter a[2]: 56 Enter a[3]: 73 Enter a[4]: 23
Sum of elements = 207 |
How it works: The first for loop asks the user to enter five elements into the array. The second for loop reads all the elements of an array one by one and accumulate the sum of all the elements in the variable s. Note that it is necessary to initialize the variable s to 0, otherwise, we will get the wrong answer because of the garbage value of s.
Initializing Array
When an array is declared inside a function the elements of the array have garbage value. If an array is global or static, then its elements are automatically initialized to 0. We can explicitly initialize elements of an array at the time of declaration using the following syntax:
Syntax: datatype array_name[size] = { val1, val2, val3, ..... ValN };
Datatype is the type of elements of an array.
Array_name is the variable name, which must be any valid identifier.
Size is the size of the array.
Val1, val2 ... Are the constants known as initializers. Each value is separated by a comma(,) and then there is a semi-colon (;) after the closing curly brace (}).
Here is are some examples:
1 2 3 | Float temp[5] = {12.3, 4.1, 3.8, 9.5, 4.5}; // an array of 5 floats
Int arr[9] = {11, 22, 33, 44, 55, 66, 77, 88, 99}; // an array of 9 ints |
While initializing 1-D array it is optional to specify the size of the array, so you can also write the above statements as:
1 2 3 | Float temp[] = {12.3, 4.1, 3.8, 9.5, 4.5}; // an array of 5 floats
Int arr[] = {11, 22, 33, 44, 55, 66, 77, 88, 99}; // an array of 9 ints |
If the number of initializers is less than the specified size then the remaining elements of the array are assigned a value of 0.
Float temp[5] = {12.3, 4.1};
Here the size of temp array is 5 but there are only two initializers. After this initialization the elements of the array are as follows:
Temp[0] is 12.3
temp[1] is 4.1
temp[2] is 0
temp[3] is 0
temp[4] is 0
If the number of initializers is greater than the size of the array then the old compilers will report an error. However, most new compilers simply issue a warning message.
Int num[5] = {1, 2, 3, 4, 5, 6, 7, 8} // Error in old compilers, warning in new ones
The following program finds the highest and lowest elements in an array.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | #include<stdio.h> #define SIZE 10
Int main() { Int my_arr[SIZE] = {34,56,78,15,43,71,89,34,70,91}; Int i, max, min;
Max = min = my_arr[0];
For(i = 0; i < SIZE; i++) { // if value of current element is greater than previous value // then assign new value to max If(my_arr[i] > max) { Max = my_arr[i]; }
// if the value of current element is less than previous element // then assign new value to min If(my_arr[i] < min) { Min = my_arr[i]; } }
Printf("Lowest value = %d\n", min); Printf("Highest value = %d", max);
// signal to operating system everything works fine Return 0; } |
Expected Output:
1 2 | Lowest value = 15 Highest value = 91 |
How it works: In line 6, first, we have declared and initialized an array of 10 integers. In the next line, we have declared three more variables of type int namely: i, max and min. In line 9, we have assigned the value of the first element of my_arr to max and min. A for loop is used to iterate through all the elements of an array. Inside the for loop, the first if condition (my_arr[i] > max) checks whether the current element is greater than max, if it is, we assign the value of the current element to max.
The second if statement checks whether the value of the current element is smaller than the value of min. If it is, we assign the value of the current element to min. This process continues until there are elements in the array left to iterate.
When the process is finished, max and min variables will have maximum and minimum values respectively.
2D Array
2D array can be defined as an array of arrays. The 2D array is organized as matrices which can be represented as the collection of rows and columns.
However, 2D arrays are created to implement a relational database look alike data structure. It provides ease of holding bulk of data at once which can be passed to any number of functions wherever required.
How to declare 2D Array
The syntax of declaring two dimensional array is very much similar to that of a one dimensional array, given as follows.
- Int arr[max_rows][max_columns];
However, It produces the data structure which looks like following.
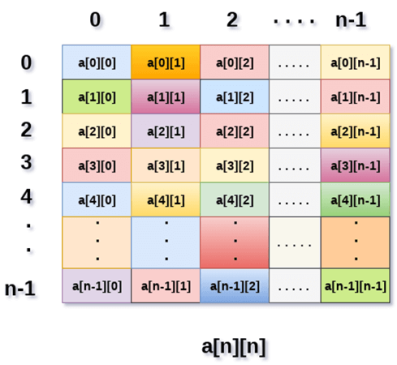
Above image shows the two dimensional array, the elements are organized in the form of rows and columns. First element of the first row is represented by a[0][0] where the number shown in the first index is the number of that row while the number shown in the second index is the number of the column.
How do we access data in a 2D array
Due to the fact that the elements of 2D arrays can be random accessed. Similar to one dimensional arrays, we can access the individual cells in a 2D array by using the indices of the cells. There are two indices attached to a particular cell, one is its row number while the other is its column number.
However, we can store the value stored in any particular cell of a 2D array to some variable x by using the following syntax.
- Int x = a[i][j];
Where i and j is the row and column number of the cell respectively.
We can assign each cell of a 2D array to 0 by using the following code:
- For ( int i=0; i<n ;i++)
- {
- For (int j=0; j<n; j++)
- {
- a[i][j] = 0;
- }
- }
Initializing 2D Arrays
We know that, when we declare and initialize one dimensional array in C programming simultaneously, we don't need to specify the size of the array. However this will not work with 2D arrays. We will have to define at least the second dimension of the array.
The syntax to declare and initialize the 2D array is given as follows.
- Int arr[2][2] = {0,1,2,3};
The number of elements that can be present in a 2D array will always be equal to (number of rows * number of columns).
Example : Storing User's data into a 2D array and printing it.
C Example :
- #include <stdio.h>
- Void main ()
- {
- Int arr[3][3],i,j;
- For (i=0;i<3;i++)
- {
- For (j=0;j<3;j++)
- {
- Printf("Enter a[%d][%d]: ",i,j);
- Scanf("%d",&arr[i][j]);
- }
- }
- Printf("\n printing the elements ....\n");
- For(i=0;i<3;i++)
- {
- Printf("\n");
- For (j=0;j<3;j++)
- {
- Printf("%d\t",arr[i][j]);
- }
- }
- }
Java Example
- Import java.util.Scanner;
- Publicclass TwoDArray {
- Publicstaticvoid main(String[] args) {
- Int[][] arr = newint[3][3];
- Scanner sc = new Scanner(System.in);
- For (inti =0;i<3;i++)
- {
- For(intj=0;j<3;j++)
- {
- System.out.print("Enter Element");
- Arr[i][j]=sc.nextInt();
- System.out.println();
- }
- }
- System.out.println("Printing Elements...");
- For(inti=0;i<3;i++)
- {
- System.out.println();
- For(intj=0;j<3;j++)
- {
- System.out.print(arr[i][j]+"\t");
- }
- }
- }
- }
C# Example
- Using System;
- Public class Program
- {
- Public static void Main()
- {
- Int[,] arr = new int[3,3];
- For (int i=0;i<3;i++)
- {
- For (int j=0;j<3;j++)
- {
- Console.WriteLine("Enter Element");
- Arr[i,j]= Convert.ToInt32(Console.ReadLine());
- }
- }
- Console.WriteLine("Printing Elements...");
- For (int i=0;i<3;i++)
- {
- Console.WriteLine();
- For (int j=0;j<3;j++)
- {
- Console.Write(arr[i,j]+" ");
- }
- }
- }
- }
Mapping 2D array to 1D array
When it comes to map a 2 dimensional array, most of us might think that why this mapping is required. However, 2 D arrays exists from the user point of view. 2D arrays are created to implement a relational database table lookalike data structure, in computer memory, the storage technique for 2D array is similar to that of an one dimensional array.
The size of a two dimensional array is equal to the multiplication of number of rows and the number of columns present in the array. We do need to map two dimensional array to the one dimensional array in order to store them in the memory.
A 3 X 3 two dimensional array is shown in the following image. However, this array needs to be mapped to a one dimensional array in order to store it into the memory.
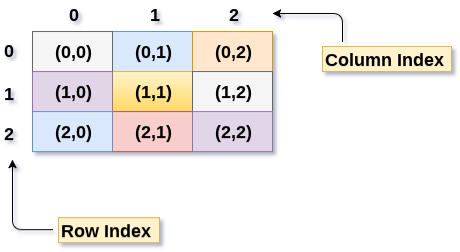
There are two main techniques of storing 2D array elements into memory
1. Row Major ordering
In row major ordering, all the rows of the 2D array are stored into the memory contiguously. Considering the array shown in the above image, its memory allocation according to row major order is shown as follows.
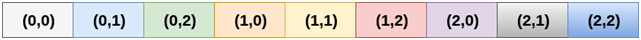
First, the 1st row of the array is stored into the memory completely, then the 2nd row of the array is stored into the memory completely and so on till the last row.
2. Column Major ordering
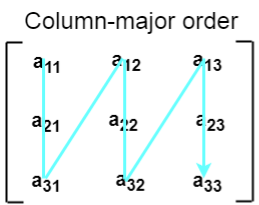
According to the column major ordering, all the columns of the 2D array are stored into the memory contiguously. The memory allocation of the array which is shown in in the above image is given as follows.
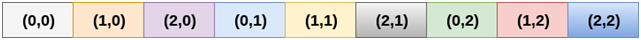
First, the 1st column of the array is stored into the memory completely, then the 2nd row of the array is stored into the memory completely and so on till the last column of the array.
Calculating the Address of the random element of a 2D array
Due to the fact that, there are two different techniques of storing the two dimensional array into the memory, there are two different formulas to calculate the address of a random element of the 2D array.
By Row Major Order
If array is declared by a[m][n] where m is the number of rows while n is the number of columns, then address of an element a[i][j] of the array stored in row major order is calculated as,
- Address(a[i][j]) = B. A. + (i * n + j) * size
Where, B. A. Is the base address or the address of the first element of the array a[0][0] .
Example :
- a[10...30, 55...75], base address of the array (BA) = 0, size of an element = 4 bytes .
- Find the location of a[15][68].
- Address(a[15][68]) = 0 +
- ((15 - 10) x (68 - 55 + 1) + (68 - 55)) x 4
- = (5 x 14 + 13) x 4
- = 83 x 4
- = 332 answer
By Column major order
If array is declared by a[m][n] where m is the number of rows while n is the number of columns, then address of an element a[i][j] of the array stored in row major order is calculated as,
- Address(a[i][j]) = ((j*m)+i)*Size + BA
Where BA is the base address of the array.
Example:
- A [-5 ... +20][20 ... 70], BA = 1020, Size of element = 8 bytes. Find the location of a[0][30].
- Address [A[0][30]) = ((30-20) x 24 + 5) x 8 + 1020 = 245 x 8 + 1020 = 2980 bytes
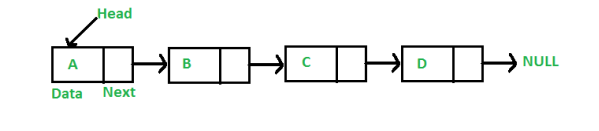
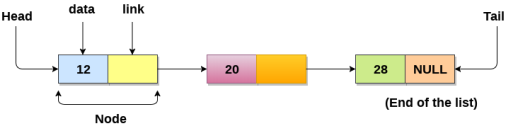
A linked list is a sequence of data structures, which are connected together via links.
Linked List is a sequence of links which contains items. Each link contains a connection to another link. Linked list is the second most-used data structure after array. Following are the important terms to understand the concept of Linked List.
- Link − Each link of a linked list can store a data called an element.
- Next − Each link of a linked list contains a link to the next link called Next.
- LinkedList − A Linked List contains the connection link to the first link called First.
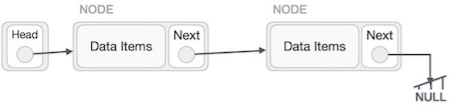
Linked List Representation
Linked list can be visualized as a chain of nodes, where every node points to the next node.

As per the above illustration, following are the important points to be considered.
- Linked List contains a link element called first.
- Each link carries a data field(s) and a link field called next.
- Each link is linked with its next link using its next link.
- Last link carries a link as null to mark the end of the list.
Types of Linked List
Following are the various types of linked list.
- Simple Linked List − Item navigation is forward only.
- Doubly Linked List − Items can be navigated forward and backward.
- Circular Linked List − Last item contains link of the first element as next and the first element has a link to the last element as previous.
Basic Operations
Following are the basic operations supported by a list.
- Insertion − Adds an element at the beginning of the list.
- Deletion − Deletes an element at the beginning of the list.
- Display − Displays the complete list.
- Search − Searches an element using the given key.
- Delete − Deletes an element using the given key.
Insertion Operation
Adding a new node in linked list is a more than one step activity. We shall learn this with diagrams here. First, create a node using the same structure and find the location where it has to be inserted.
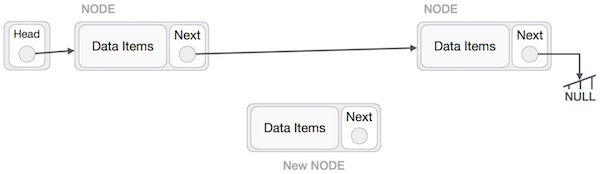
Imagine that we are inserting a node B (NewNode), between A (LeftNode) and C (RightNode). Then point B.next to C −
NewNode.next −> RightNode;
It should look like this −
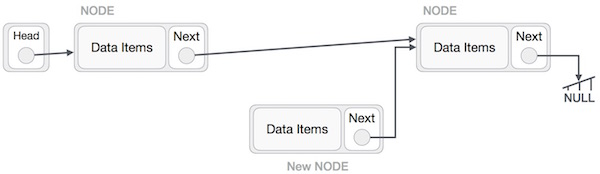
Now, the next node at the left should point to the new node.
LeftNode.next −> NewNode;
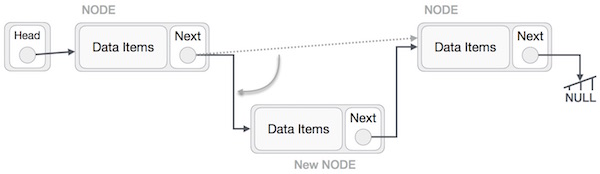
This will put the new node in the middle of the two. The new list should look like this −

Similar steps should be taken if the node is being inserted at the beginning of the list. While inserting it at the end, the second last node of the list should point to the new node and the new node will point to NULL.
Deletion Operation
Deletion is also a more than one step process. We shall learn with pictorial representation. First, locate the target node to be removed, by using searching algorithms.

The left (previous) node of the target node now should point to the next node of the target node −
LeftNode.next −> TargetNode.next;

This will remove the link that was pointing to the target node. Now, using the following code, we will remove what the target node is pointing at.
TargetNode.next −> NULL;

We need to use the deleted node. We can keep that in memory otherwise we can simply deallocate memory and wipe off the target node completely.
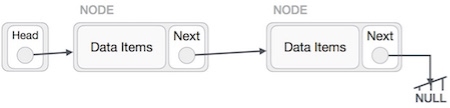
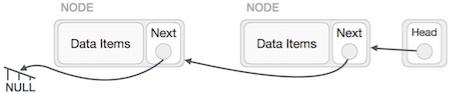
Reverse Operation
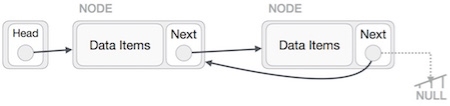
This operation is a thorough one. We need to make the last node to be pointed by the head node and reverse the whole linked list.
First, we traverse to the end of the list. It should be pointing to NULL. Now, we shall make it point to its previous node −
We have to make sure that the last node is not the last node. So we'll have some temp node, which looks like the head node pointing to the last node. Now, we shall make all left side nodes point to their previous nodes one by one.
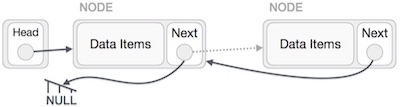
Except the node (first node) pointed by the head node, all nodes should point to their predecessor, making them their new successor. The first node will point to NULL.
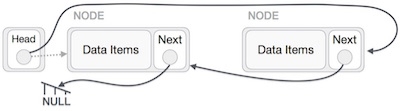
We'll make the head node point to the new first node by using the temp node.
A linked list is a sequence of data structures, which are connected together via links. Linked List is a sequence of links which contains items. Each link contains a connection to another link. Linked list is the second most-used data structure after array.
Implementation
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
Struct node {
Int data;
Int key;
Struct node *next;
};
Struct node *head = NULL;
Struct node *current = NULL;
//display the list
Void printList() {
Struct node *ptr = head;
Printf("\n[ ");
//start from the beginning
While(ptr != NULL) {
Printf("(%d,%d) ",ptr->key,ptr->data);
Ptr = ptr->next;
}
Printf(" ]");
}
//insert link at the first location
Void insertFirst(int key, int data) {
//create a link
Struct node *link = (struct node*) malloc(sizeof(struct node));
Link->key = key;
Link->data = data;
//point it to old first node
Link->next = head;
//point first to new first node
Head = link;
}
//delete first item
Struct node* deleteFirst() {
//save reference to first link
Struct node *tempLink = head;
//mark next to first link as first
Head = head->next;
//return the deleted link
Return tempLink;
}
//is list empty
Bool isEmpty() {
Return head == NULL;
}
Int length() {
Int length = 0;
Struct node *current;
For(current = head; current != NULL; current = current->next) {
Length++;
}
Return length;
}
//find a link with given key
Struct node* find(int key) {
//start from the first link
Struct node* current = head;
//if list is empty
If(head == NULL) {
Return NULL;
}
//navigate through list
While(current->key != key) {
//if it is last node
If(current->next == NULL) {
Return NULL;
} else {
//go to next link
Current = current->next;
}
}
//if data found, return the current Link
Return current;
}
//delete a link with given key
Struct node* delete(int key) {
//start from the first link
Struct node* current = head;
Struct node* previous = NULL;
//if list is empty
If(head == NULL) {
Return NULL;
}
//navigate through list
While(current->key != key) {
//if it is last node
If(current->next == NULL) {
Return NULL;
} else {
//store reference to current link
Previous = current;
//move to next link
Current = current->next;
}
}
//found a match, update the link
If(current == head) {
//change first to point to next link
Head = head->next;
} else {
//bypass the current link
Previous->next = current->next;
}
Return current;
}
Void sort() {
Int i, j, k, tempKey, tempData;
Struct node *current;
Struct node *next;
Int size = length();
k = size ;
For ( i = 0 ; i < size - 1 ; i++, k-- ) {
Current = head;
Next = head->next;
For ( j = 1 ; j < k ; j++ ) {
If ( current->data > next->data ) {
TempData = current->data;
Current->data = next->data;
Next->data = tempData;
TempKey = current->key;
Current->key = next->key;
Next->key = tempKey;
}
Current = current->next;
Next = next->next;
}
}
}
Void reverse(struct node** head_ref) {
Struct node* prev = NULL;
Struct node* current = *head_ref;
Struct node* next;
While (current != NULL) {
Next = current->next;
Current->next = prev;
Prev = current;
Current = next;
}
*head_ref = prev;
}
Void main() {
InsertFirst(1,10);
InsertFirst(2,20);
InsertFirst(3,30);
InsertFirst(4,1);
InsertFirst(5,40);
InsertFirst(6,56);
Printf("Original List: ");
//print list
PrintList();
While(!isEmpty()) {
Struct node *temp = deleteFirst();
Printf("\nDeleted value:");
Printf("(%d,%d) ",temp->key,temp->data);
}
Printf("\nList after deleting all items: ");
PrintList();
InsertFirst(1,10);
InsertFirst(2,20);
InsertFirst(3,30);
InsertFirst(4,1);
InsertFirst(5,40);
InsertFirst(6,56);
Printf("\nRestored List: ");
PrintList();
Printf("\n");
Struct node *foundLink = find(4);
If(foundLink != NULL) {
Printf("Element found: ");
Printf("(%d,%d) ",foundLink->key,foundLink->data);
Printf("\n");
} else {
Printf("Element not found.");
}
Delete(4);
Printf("List after deleting an item: ");
PrintList();
Printf("\n");
FoundLink = find(4);
If(foundLink != NULL) {
Printf("Element found: ");
Printf("(%d,%d) ",foundLink->key,foundLink->data);
Printf("\n");
} else {
Printf("Element not found.");
}
Printf("\n");
Sort();
Printf("List after sorting the data: ");
PrintList();
Reverse(&head);
Printf("\nList after reversing the data: ");
PrintList();
}
If we compile and run the above program, it will produce the following result −
Output
Original List:
[ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ]
Deleted value:(6,56)
Deleted value:(5,40)
Deleted value:(4,1)
Deleted value:(3,30)
Deleted value:(2,20)
Deleted value:(1,10)
List after deleting all items:
[ ]
Restored List:
[ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ]
Element found: (4,1)
List after deleting an item:
[ (6,56) (5,40) (3,30) (2,20) (1,10) ]
Element not found.
List after sorting the data:
[ (1,10) (2,20) (3,30) (5,40) (6,56) ]
List after reversing the data:
[ (6,56) (5,40) (3,30) (2,20) (1,10) ]
Linked List
- Linked List can be defined as collection of objects called nodes that are randomly stored in the memory.
- A node contains two fields i.e. data stored at that particular address and the pointer which contains the address of the next node in the memory.
- The last node of the list contains pointer to the null.
Uses of Linked List
- The list is not required to be contiguously present in the memory. The node can reside any where in the memory and linked together to make a list. This achieves optimized utilization of space.
- List size is limited to the memory size and doesn't need to be declared in advance.
- Empty node can not be present in the linked list.
- We can store values of primitive types or objects in the singly linked list.
Why use linked list over array?
Till now, we were using array data structure to organize the group of elements that are to be stored individually in the memory. However, Array has several advantages and disadvantages which must be known in order to decide the data structure which will be used throughout the program.
Array contains following limitations:
- The size of array must be known in advance before using it in the program.
- Increasing size of the array is a time taking process. It is almost impossible to expand the size of the array at run time.
- All the elements in the array need to be contiguously stored in the memory. Inserting any element in the array needs shifting of all its predecessors.
Linked list is the data structure which can overcome all the limitations of an array. Using linked list is useful because,
- It allocates the memory dynamically. All the nodes of linked list are non-contiguously stored in the memory and linked together with the help of pointers.
- Sizing is no longer a problem since we do not need to define its size at the time of declaration. List grows as per the program's demand and limited to the available memory space.
Singly linked list or One way chain
Singly linked list can be defined as the collection of ordered set of elements. The number of elements may vary according to need of the program. A node in the singly linked list consist of two parts: data part and link part. Data part of the node stores actual information that is to be represented by the node while the link part of the node stores the address of its immediate successor.
One way chain or singly linked list can be traversed only in one direction. In other words, we can say that each node contains only next pointer, therefore we can not traverse the list in the reverse direction.
Consider an example where the marks obtained by the student in three subjects are stored in a linked list as shown in the figure.
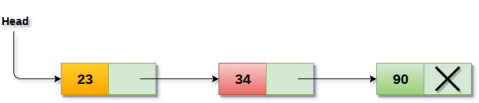
In the above figure, the arrow represents the links. The data part of every node contains the marks obtained by the student in the different subject. The last node in the list is identified by the null pointer which is present in the address part of the last node. We can have as many elements we require, in the data part of the list.
Complexity
Data Structure | Time Complexity | Space Compleity | |||||||
| Average | Worst | Worst | ||||||
| Access | Search | Insertion | Deletion | Access | Search | Insertion | Deletion |
|
Singly Linked List | θ(n) | θ(n) | θ(1) | θ(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
Operations on Singly Linked List
There are various operations which can be performed on singly linked list. A list of all such operations is given below.
Node Creation
- Struct node
- {
- Int data;
- Struct node *next;
- };
- Struct node *head, *ptr;
- Ptr = (struct node *)malloc(sizeof(struct node *));
Insertion
The insertion into a singly linked list can be performed at different positions. Based on the position of the new node being inserted, the insertion is categorized into the following categories.
SN | Operation | Description |
1 | Insertion at beginning | It involves inserting any element at the front of the list. We just need to a few link adjustments to make the new node as the head of the list. |
2 | Insertion at end of the list | It involves insertion at the last of the linked list. The new node can be inserted as the only node in the list or it can be inserted as the last one. Different logics are implemented in each scenario. |
3 | Insertion after specified node | It involves insertion after the specified node of the linked list. We need to skip the desired number of nodes in order to reach the node after which the new node will be inserted. . |
Deletion and Traversing
The Deletion of a node from a singly linked list can be performed at different positions. Based on the position of the node being deleted, the operation is categorized into the following categories.
SN | Operation | Description |
1 | Deletion at beginning | It involves deletion of a node from the beginning of the list. This is the simplest operation among all. It just need a few adjustments in the node pointers. |
2 | Deletion at the end of the list | It involves deleting the last node of the list. The list can either be empty or full. Different logic is implemented for the different scenarios. |
3 | Deletion after specified node | It involves deleting the node after the specified node in the list. We need to skip the desired number of nodes to reach the node after which the node will be deleted. This requires traversing through the list. |
4 | Traversing | In traversing, we simply visit each node of the list at least once in order to perform some specific operation on it, for example, printing data part of each node present in the list. |
5 | Searching | In searching, we match each element of the list with the given element. If the element is found on any of the location then location of that element is returned otherwise null is returned. . |
Linked List: Menu Driven Program
- #include<stdio.h>
- #include<stdlib.h>
- Struct node
- {
- Int data;
- Struct node *next;
- };
- Struct node *head;
- Void beginsert ();
- Void lastinsert ();
- Void randominsert();
- Void begin_delete();
- Void last_delete();
- Void random_delete();
- Void display();
- Void search();
- Void main ()
- {
- Int choice =0;
- While(choice != 9)
- {
- Printf("\n\n*********Main Menu*********\n");
- Printf("\nChoose one option from the following list ...\n");
- Printf("\n===============================================\n");
- Printf("\n1.Insert in begining\n2.Insert at last\n3.Insert at any random location\n4.Delete from Beginning\n
- 5.Delete from last\n6.Delete node after specified location\n7.Search for an element\n8.Show\n9.Exit\n");
- Printf("\nEnter your choice?\n");
- Scanf("\n%d",&choice);
- Switch(choice)
- {
- Case 1:
- Beginsert();
- Break;
- Case 2:
- Lastinsert();
- Break;
- Case 3:
- Randominsert();
- Break;
- Case 4:
- Begin_delete();
- Break;
- Case 5:
- Last_delete();
- Break;
- Case 6:
- Random_delete();
- Break;
- Case 7:
- Search();
- Break;
- Case 8:
- Display();
- Break;
- Case 9:
- Exit(0);
- Break;
- Default:
- Printf("Please enter valid choice..");
- }
- }
- }
- Void beginsert()
- {
- Struct node *ptr;
- Int item;
- Ptr = (struct node *) malloc(sizeof(struct node *));
- If(ptr == NULL)
- {
- Printf("\nOVERFLOW");
- }
- Else
- {
- Printf("\nEnter value\n");
- Scanf("%d",&item);
- Ptr->data = item;
- Ptr->next = head;
- Head = ptr;
- Printf("\nNode inserted");
- }
- }
- Void lastinsert()
- {
- Struct node *ptr,*temp;
- Int item;
- Ptr = (struct node*)malloc(sizeof(struct node));
- If(ptr == NULL)
- {
- Printf("\nOVERFLOW");
- }
- Else
- {
- Printf("\nEnter value?\n");
- Scanf("%d",&item);
- Ptr->data = item;
- If(head == NULL)
- {
- Ptr -> next = NULL;
- Head = ptr;
- Printf("\nNode inserted");
- }
- Else
- {
- Temp = head;
- While (temp -> next != NULL)
- {
- Temp = temp -> next;
- }
- Temp->next = ptr;
- Ptr->next = NULL;
- Printf("\nNode inserted");
- }
- }
- }
- Void randominsert()
- {
- Int i,loc,item;
- Struct node *ptr, *temp;
- Ptr = (struct node *) malloc (sizeof(struct node));
- If(ptr == NULL)
- {
- Printf("\nOVERFLOW");
- }
- Else
- {
- Printf("\nEnter element value");
- Scanf("%d",&item);
- Ptr->data = item;
- Printf("\nEnter the location after which you want to insert ");
- Scanf("\n%d",&loc);
- Temp=head;
- For(i=0;i<loc;i++)
- {
- Temp = temp->next;
- If(temp == NULL)
- {
- Printf("\ncan't insert\n");
- Return;
- }
- }
- Ptr ->next = temp ->next;
- Temp ->next = ptr;
- Printf("\nNode inserted");
- }
- }
- Void begin_delete()
- {
- Struct node *ptr;
- If(head == NULL)
- {
- Printf("\nList is empty\n");
- }
- Else
- {
- Ptr = head;
- Head = ptr->next;
- Free(ptr);
- Printf("\nNode deleted from the begining ...\n");
- }
- }
- Void last_delete()
- {
- Struct node *ptr,*ptr1;
- If(head == NULL)
- {
- Printf("\nlist is empty");
- }
- Else if(head -> next == NULL)
- {
- Head = NULL;
- Free(head);
- Printf("\nOnly node of the list deleted ...\n");
- }
- Else
- {
- Ptr = head;
- While(ptr->next != NULL)
- {
- Ptr1 = ptr;
- Ptr = ptr ->next;
- }
- Ptr1->next = NULL;
- Free(ptr);
- Printf("\nDeleted Node from the last ...\n");
- }
- }
- Void random_delete()
- {
- Struct node *ptr,*ptr1;
- Int loc,i;
- Printf("\n Enter the location of the node after which you want to perform deletion \n");
- Scanf("%d",&loc);
- Ptr=head;
- For(i=0;i<loc;i++)
- {
- Ptr1 = ptr;
- Ptr = ptr->next;
- If(ptr == NULL)
- {
- Printf("\nCan't delete");
- Return;
- }
- }
- Ptr1 ->next = ptr ->next;
- Free(ptr);
- Printf("\nDeleted node %d ",loc+1);
- }
- Void search()
- {
- Struct node *ptr;
- Int item,i=0,flag;
- Ptr = head;
- If(ptr == NULL)
- {
- Printf("\nEmpty List\n");
- }
- Else
- {
- Printf("\nEnter item which you want to search?\n");
- Scanf("%d",&item);
- While (ptr!=NULL)
- {
- If(ptr->data == item)
- {
- Printf("item found at location %d ",i+1);
- Flag=0;
- }
- Else
- {
- Flag=1;
- }
- i++;
- Ptr = ptr -> next;
- }
- If(flag==1)
- {
- Printf("Item not found\n");
- }
- }
- }
- Void display()
- {
- Struct node *ptr;
- Ptr = head;
- If(ptr == NULL)
- {
- Printf("Nothing to print");
- }
- Else
- {
- Printf("\nprinting values . . . . .\n");
- While (ptr!=NULL)
- {
- Printf("\n%d",ptr->data);
- Ptr = ptr -> next;
- }
- }
- }
Output:
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete node after specified location
7.Search for an element
8.Show
9.Exit
Enter your choice?
1
Enter value
1
Node inserted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete node after specified location
7.Search for an element
8.Show
9.Exit
Enter your choice?
2
Enter value?
2
Node inserted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete node after specified location
7.Search for an element
8.Show
9.Exit
Enter your choice?
3
Enter element value1
Enter the location after which you want to insert 1
Node inserted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete node after specified location
7.Search for an element
8.Show
9.Exit
Enter your choice?
8
Printing values . . . . .
1
2
1
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete node after specified location
7.Search for an element
8.Show
9.Exit
Enter your choice?
2
Enter value?
123
Node inserted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete node after specified location
7.Search for an element
8.Show
9.Exit
Enter your choice?
1
Enter value
1234
Node inserted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete node after specified location
7.Search for an element
8.Show
9.Exit
Enter your choice?
4
Node deleted from the begining ...
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete node after specified location
7.Search for an element
8.Show
9.Exit
Enter your choice?
5
Deleted Node from the last ...
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in beginning
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete node after specified location
7.Search for an element
8.Show
9.Exit
Enter your choice?
6
Enter the location of the node after which you want to perform deletion
1
Deleted node 2
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete node after specified location
7.Search for an element
8.Show
9.Exit
Enter your choice?
8
Printing values . . . . .
1
1
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete node after specified location
7.Search for an element
8.Show
9.Exit
Enter your choice?
7
Enter item which you want to search?
1
Item found at location 1
Item found at location 2
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete node after specified location
7.Search for an element
8.Show
9.Exit
Enter your choice?
9
Doubly linked list is a complex type of linked list in which a node contains a pointer to the previous as well as the next node in the sequence. Therefore, in a doubly linked list, a node consists of three parts: node data, pointer to the next node in sequence (next pointer) , pointer to the previous node (previous pointer). A sample node in a doubly linked list is shown in the figure.
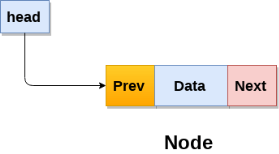
A doubly linked list containing three nodes having numbers from 1 to 3 in their data part, is shown in the following image.
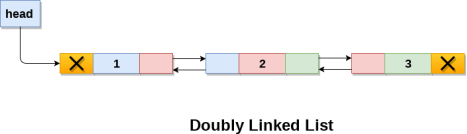
In C, structure of a node in doubly linked list can be given as :
- Struct node
- {
- Struct node *prev;
- Int data;
- Struct node *next;
- }
The prev part of the first node and the next part of the last node will always contain null indicating end in each direction.
In a singly linked list, we could traverse only in one direction, because each node contains address of the next node and it doesn't have any record of its previous nodes. However, doubly linked list overcome this limitation of singly linked list. Due to the fact that, each node of the list contains the address of its previous node, we can find all the details about the previous node as well by using the previous address stored inside the previous part of each node.
Memory Representation of a doubly linked list
Memory Representation of a doubly linked list is shown in the following image. Generally, doubly linked list consumes more space for every node and therefore, causes more expansive basic operations such as insertion and deletion. However, we can easily manipulate the elements of the list since the list maintains pointers in both the directions (forward and backward).
In the following image, the first element of the list that is i.e. 13 stored at address 1. The head pointer points to the starting address 1. Since this is the first element being added to the list therefore the prev of the list contains null. The next node of the list resides at address 4 therefore the first node contains 4 in its next pointer.
We can traverse the list in this way until we find any node containing null or -1 in its next part.
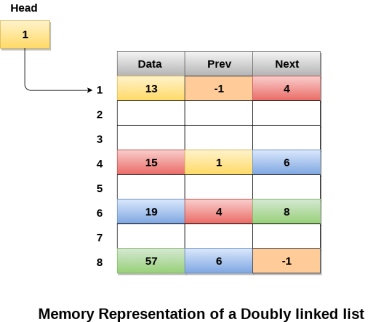
Operations on doubly linked list
Node Creation
- Struct node
- {
- Struct node *prev;
- Int data;
- Struct node *next;
- };
- Struct node *head;
All the remaining operations regarding doubly linked list are described in the following table.
SN | Operation | Description |
1 | Insertion at beginning
| Adding the node into the linked list at beginning. |
2 | Insertion at end | Adding the node into the linked list to the end. |
3 | Insertion after specified node | Adding the node into the linked list after the specified node. |
4 | Deletion at beginning | Removing the node from beginning of the list |
5 | Deletion at the end | Removing the node from end of the list. |
6 | Deletion of the node having given data | Removing the node which is present just after the node containing the given data. |
7 | Searching | Comparing each node data with the item to be searched and return the location of the item in the list if the item found else return null. |
8 | Traversing | Visiting each node of the list at least once in order to perform some specific operation like searching, sorting, display, etc. |
Menu Driven Program to implement all the operations of doubly linked list
- #include<stdio.h>
- #include<stdlib.h>
- Struct node
- {
- Struct node *prev;
- Struct node *next;
- Int data;
- };
- Struct node *head;
- Void insertion_beginning();
- Void insertion_last();
- Void insertion_specified();
- Void deletion_beginning();
- Void deletion_last();
- Void deletion_specified();
- Void display();
- Void search();
- Void main ()
- {
- Int choice =0;
- While(choice != 9)
- {
- Printf("\n*********Main Menu*********\n");
- Printf("\nChoose one option from the following list ...\n");
- Printf("\n===============================================\n");
- Printf("\n1.Insert in begining\n2.Insert at last\n3.Insert at any random location\n4.Delete from Beginning\n
- 5.Delete from last\n6.Delete the node after the given data\n7.Search\n8.Show\n9.Exit\n");
- Printf("\nEnter your choice?\n");
- Scanf("\n%d",&choice);
- Switch(choice)
- {
- Case 1:
- Insertion_beginning();
- Break;
- Case 2:
- Insertion_last();
- Break;
- Case 3:
- Insertion_specified();
- Break;
- Case 4:
- Deletion_beginning();
- Break;
- Case 5:
- Deletion_last();
- Break;
- Case 6:
- Deletion_specified();
- Break;
- Case 7:
- Search();
- Break;
- Case 8:
- Display();
- Break;
- Case 9:
- Exit(0);
- Break;
- Default:
- Printf("Please enter valid choice..");
- }
- }
- }
- Void insertion_beginning()
- {
- Struct node *ptr;
- Int item;
- Ptr = (struct node *)malloc(sizeof(struct node));
- If(ptr == NULL)
- {
- Printf("\nOVERFLOW");
- }
- Else
- {
- Printf("\nEnter Item value");
- Scanf("%d",&item);
- If(head==NULL)
- {
- Ptr->next = NULL;
- Ptr->prev=NULL;
- Ptr->data=item;
- Head=ptr;
- }
- Else
- {
- Ptr->data=item;
- Ptr->prev=NULL;
- Ptr->next = head;
- Head->prev=ptr;
- Head=ptr;
- }
- Printf("\nNode inserted\n");
- }
- }
- Void insertion_last()
- {
- Struct node *ptr,*temp;
- Int item;
- Ptr = (struct node *) malloc(sizeof(struct node));
- If(ptr == NULL)
- {
- Printf("\nOVERFLOW");
- }
- Else
- {
- Printf("\nEnter value");
- Scanf("%d",&item);
- Ptr->data=item;
- If(head == NULL)
- {
- Ptr->next = NULL;
- Ptr->prev = NULL;
- Head = ptr;
- }
- Else
- {
- Temp = head;
- While(temp->next!=NULL)
- {
- Temp = temp->next;
- }
- Temp->next = ptr;
- Ptr ->prev=temp;
- Ptr->next = NULL;
- }
- }
- Printf("\nnode inserted\n");
- }
- Void insertion_specified()
- {
- Struct node *ptr,*temp;
- Int item,loc,i;
- Ptr = (struct node *)malloc(sizeof(struct node));
- If(ptr == NULL)
- {
- Printf("\n OVERFLOW");
- }
- Else
- {
- Temp=head;
- Printf("Enter the location");
- Scanf("%d",&loc);
- For(i=0;i<loc;i++)
- {
- Temp = temp->next;
- If(temp == NULL)
- {
- Printf("\n There are less than %d elements", loc);
- Return;
- }
- }
- Printf("Enter value");
- Scanf("%d",&item);
- Ptr->data = item;
- Ptr->next = temp->next;
- Ptr -> prev = temp;
- Temp->next = ptr;
- Temp->next->prev=ptr;
- Printf("\nnode inserted\n");
- }
- }
- Void deletion_beginning()
- {
- Struct node *ptr;
- If(head == NULL)
- {
- Printf("\n UNDERFLOW");
- }
- Else if(head->next == NULL)
- {
- Head = NULL;
- Free(head);
- Printf("\nnode deleted\n");
- }
- Else
- {
- Ptr = head;
- Head = head -> next;
- Head -> prev = NULL;
- Free(ptr);
- Printf("\nnode deleted\n");
- }
- }
- Void deletion_last()
- {
- Struct node *ptr;
- If(head == NULL)
- {
- Printf("\n UNDERFLOW");
- }
- Else if(head->next == NULL)
- {
- Head = NULL;
- Free(head);
- Printf("\nnode deleted\n");
- }
- Else
- {
- Ptr = head;
- If(ptr->next != NULL)
- {
- Ptr = ptr -> next;
- }
- Ptr -> prev -> next = NULL;
- Free(ptr);
- Printf("\nnode deleted\n");
- }
- }
- Void deletion_specified()
- {
- Struct node *ptr, *temp;
- Int val;
- Printf("\n Enter the data after which the node is to be deleted : ");
- Scanf("%d", &val);
- Ptr = head;
- While(ptr -> data != val)
- Ptr = ptr -> next;
- If(ptr -> next == NULL)
- {
- Printf("\nCan't delete\n");
- }
- Else if(ptr -> next -> next == NULL)
- {
- Ptr ->next = NULL;
- }
- Else
- {
- Temp = ptr -> next;
- Ptr -> next = temp -> next;
- Temp -> next -> prev = ptr;
- Free(temp);
- Printf("\nnode deleted\n");
- }
- }
- Void display()
- {
- Struct node *ptr;
- Printf("\n printing values...\n");
- Ptr = head;
- While(ptr != NULL)
- {
- Printf("%d\n",ptr->data);
- Ptr=ptr->next;
- }
- }
- Void search()
- {
- Struct node *ptr;
- Int item,i=0,flag;
- Ptr = head;
- If(ptr == NULL)
- {
- Printf("\nEmpty List\n");
- }
- Else
- {
- Printf("\nEnter item which you want to search?\n");
- Scanf("%d",&item);
- While (ptr!=NULL)
- {
- If(ptr->data == item)
- {
- Printf("\nitem found at location %d ",i+1);
- Flag=0;
- Break;
- }
- Else
- {
- Flag=1;
- }
- i++;
- Ptr = ptr -> next;
- }
- If(flag==1)
- {
- Printf("\nItem not found\n");
- }
- }
- }
Output
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete the node after the given data
7.Search
8.Show
9.Exit
Enter your choice?
8
Printing values...
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete the node after the given data
7.Search
8.Show
9.Exit
Enter your choice?
1
Enter Item value12
Node inserted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete the node after the given data
7.Search
8.Show
9.Exit
Enter your choice?
1
Enter Item value123
Node inserted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete the node after the given data
7.Search
8.Show
9.Exit
Enter your choice?
1
Enter Item value1234
Node inserted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete the node after the given data
7.Search
8.Show
9.Exit
Enter your choice?
8
Printing values...
1234
123
12
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete the node after the given data
7.Search
8.Show
9.Exit
Enter your choice?
2
Enter value89
Node inserted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete the node after the given data
7.Search
8.Show
9.Exit
Enter your choice?
3
Enter the location1
Enter value12345
Node inserted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete the node after the given data
7.Search
8.Show
9.Exit
Enter your choice?
8
Printing values...
1234
123
12345
12
89
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete the node after the given data
7.Search
8.Show
9.Exit
Enter your choice?
4
Node deleted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete the node after the given data
7.Search
8.Show
9.Exit
Enter your choice?
5
Node deleted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete the node after the given data
7.Search
8.Show
9.Exit
Enter your choice?
8
Printing values...
123
12345
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete the node after the given data
7.Search
8.Show
9.Exit
Enter your choice?
6
Enter the data after which the node is to be deleted : 123
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete the node after the given data
7.Search
8.Show
9.Exit
Enter your choice?
8
Printing values...
123
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete the node after the given data
7.Search
8.Show
9.Exit
Enter your choice?
7
Enter item which you want to search?
123
Item found at location 1
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete the node after the given data
7.Search
8.Show
9.Exit
Enter your choice?
6
Enter the data after which the node is to be deleted : 123
Can't delete
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Insert at any random location
4.Delete from Beginning
5.Delete from last
6.Delete the node after the given data
7.Search
8.Show
9.Exit
Enter your choice?
9
Exited..
Circular Singly Linked List
In a circular Singly linked list, the last node of the list contains a pointer to the first node of the list. We can have circular singly linked list as well as circular doubly linked list.
We traverse a circular singly linked list until we reach the same node where we started. The circular singly liked list has no beginning and no ending. There is no null value present in the next part of any of the nodes.
The following image shows a circular singly linked list.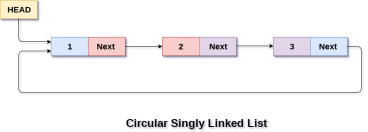
Circular linked list are mostly used in task maintenance in operating systems. There are many examples where circular linked list are being used in computer science including browser surfing where a record of pages visited in the past by the user, is maintained in the form of circular linked lists and can be accessed again on clicking the previous button.
Memory Representation of circular linked list:
In the following image, memory representation of a circular linked list containing marks of a student in 4 subjects. However, the image shows a glimpse of how the circular list is being stored in the memory. The start or head of the list is pointing to the element with the index 1 and containing 13 marks in the data part and 4 in the next part. Which means that it is linked with the node that is being stored at 4th index of the list.
However, due to the fact that we are considering circular linked list in the memory therefore the last node of the list contains the address of the first node of the list.
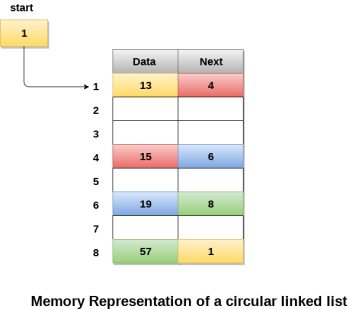
We can also have more than one number of linked list in the memory with the different start pointers pointing to the different start nodes in the list. The last node is identified by its next part which contains the address of the start node of the list. We must be able to identify the last node of any linked list so that we can find out the number of iterations which need to be performed while traversing the list.
Operations on Circular Singly linked list:
Insertion
SN | Operation | Description |
1 | Insertion at beginning | Adding a node into circular singly linked list at the beginning. |
2 | Insertion at the end | Adding a node into circular singly linked list at the end. |
Deletion & Traversing
SN | Operation | Description |
1 | Deletion at beginning | Removing the node from circular singly linked list at the beginning. |
2 | Deletion at the end | Removing the node from circular singly linked list at the end. |
3 | Searching | Compare each element of the node with the given item and return the location at which the item is present in the list otherwise return null. |
4 | Traversing | Visiting each element of the list at least once in order to perform some specific operation. |
Menu-driven program in C implementing all operations
On circular singly linked list
- #include<stdio.h>
- #include<stdlib.h>
- Struct node
- {
- Int data;
- Struct node *next;
- };
- Struct node *head;
- Void beginsert ();
- Void lastinsert ();
- Void randominsert();
- Void begin_delete();
- Void last_delete();
- Void random_delete();
- Void display();
- Void search();
- Void main ()
- {
- Int choice =0;
- While(choice != 7)
- {
- Printf("\n*********Main Menu*********\n");
- Printf("\nChoose one option from the following list ...\n");
- Printf("\n===============================================\n");
- Printf("\n1.Insert in begining\n2.Insert at last\n3.Delete from Beginning\n4.Delete from last\n5.Search for an element\n6.Show\n7.Exit\n");
- Printf("\nEnter your choice?\n");
- Scanf("\n%d",&choice);
- Switch(choice)
- {
- Case 1:
- Beginsert();
- Break;
- Case 2:
- Lastinsert();
- Break;
- Case 3:
- Begin_delete();
- Break;
- Case 4:
- Last_delete();
- Break;
- Case 5:
- Search();
- Break;
- Case 6:
- Display();
- Break;
- Case 7:
- Exit(0);
- Break;
- Default:
- Printf("Please enter valid choice..");
- }
- }
- }
- Void beginsert()
- {
- Struct node *ptr,*temp;
- Int item;
- Ptr = (struct node *)malloc(sizeof(struct node));
- If(ptr == NULL)
- {
- Printf("\nOVERFLOW");
- }
- Else
- {
- Printf("\nEnter the node data?");
- Scanf("%d",&item);
- Ptr -> data = item;
- If(head == NULL)
- {
- Head = ptr;
- Ptr -> next = head;
- }
- Else
- {
- Temp = head;
- While(temp->next != head)
- Temp = temp->next;
- Ptr->next = head;
- Temp -> next = ptr;
- Head = ptr;
- }
- Printf("\nnode inserted\n");
- }
- }
- Void lastinsert()
- {
- Struct node *ptr,*temp;
- Int item;
- Ptr = (struct node *)malloc(sizeof(struct node));
- If(ptr == NULL)
- {
- Printf("\nOVERFLOW\n");
- }
- Else
- {
- Printf("\nEnter Data?");
- Scanf("%d",&item);
- Ptr->data = item;
- If(head == NULL)
- {
- Head = ptr;
- Ptr -> next = head;
- }
- Else
- {
- Temp = head;
- While(temp -> next != head)
- {
- Temp = temp -> next;
- }
- Temp -> next = ptr;
- Ptr -> next = head;
- }
- Printf("\nnode inserted\n");
- }
- }
- Void begin_delete()
- {
- Struct node *ptr;
- If(head == NULL)
- {
- Printf("\nUNDERFLOW");
- }
- Else if(head->next == head)
- {
- Head = NULL;
- Free(head);
- Printf("\nnode deleted\n");
- }
- Else
- { ptr = head;
- While(ptr -> next != head)
- Ptr = ptr -> next;
- Ptr->next = head->next;
- Free(head);
- Head = ptr->next;
- Printf("\nnode deleted\n");
- }
- }
- Void last_delete()
- {
- Struct node *ptr, *preptr;
- If(head==NULL)
- {
- Printf("\nUNDERFLOW");
- }
- Else if (head ->next == head)
- {
- Head = NULL;
- Free(head);
- Printf("\nnode deleted\n");
- }
- Else
- {
- Ptr = head;
- While(ptr ->next != head)
- {
- Preptr=ptr;
- Ptr = ptr->next;
- }
- Preptr->next = ptr -> next;
- Free(ptr);
- Printf("\nnode deleted\n");
- }
- }
- Void search()
- {
- Struct node *ptr;
- Int item,i=0,flag=1;
- Ptr = head;
- If(ptr == NULL)
- {
- Printf("\nEmpty List\n");
- }
- Else
- {
- Printf("\nEnter item which you want to search?\n");
- Scanf("%d",&item);
- If(head ->data == item)
- {
- Printf("item found at location %d",i+1);
- Flag=0;
- }
- Else
- {
- While (ptr->next != head)
- {
- If(ptr->data == item)
- {
- Printf("item found at location %d ",i+1);
- Flag=0;
- Break;
- }
- Else
- {
- Flag=1;
- }
- i++;
- Ptr = ptr -> next;
- }
- }
- If(flag != 0)
- {
- Printf("Item not found\n");
- }
- }
- }
- Void display()
- {
- Struct node *ptr;
- Ptr=head;
- If(head == NULL)
- {
- Printf("\nnothing to print");
- }
- Else
- {
- Printf("\n printing values ... \n");
- While(ptr -> next != head)
- {
- Printf("%d\n", ptr -> data);
- Ptr = ptr -> next;
- }
- Printf("%d\n", ptr -> data);
- }
- }
Output:
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Delete from Beginning
4.Delete from last
5.Search for an element
6.Show
7.Exit
Enter your choice?
1
Enter the node data?10
Node inserted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Delete from Beginning
4.Delete from last
5.Search for an element
6.Show
7.Exit
Enter your choice?
2
Enter Data?20
Node inserted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Delete from Beginning
4.Delete from last
5.Search for an element
6.Show
7.Exit
Enter your choice?
2
Enter Data?30
Node inserted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Delete from Beginning
4.Delete from last
5.Search for an element
6.Show
7.Exit
Enter your choice?
3
Node deleted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Delete from Beginning
4.Delete from last
5.Search for an element
6.Show
7.Exit
Enter your choice?
4
Node deleted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Delete from Beginning
4.Delete from last
5.Search for an element
6.Show
7.Exit
Enter your choice?
5
Enter item which you want to search?
20
Item found at location 1
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Delete from Beginning
4.Delete from last
5.Search for an element
6.Show
7.Exit
Enter your choice?
6
Printing values ...
20
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in begining
2.Insert at last
3.Delete from Beginning
4.Delete from last
5.Search for an element
6.Show
7.Exit
Enter your choice?
7
Circular Doubly Linked List
Circular doubly linked list is a more complexed type of data structure in which a node contain pointers to its previous node as well as the next node. Circular doubly linked list doesn't contain NULL in any of the node. The last node of the list contains the address of the first node of the list. The first node of the list also contain address of the last node in its previous pointer.
A circular doubly linked list is shown in the following figure.
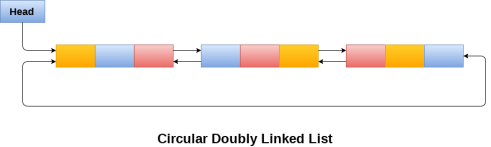
Due to the fact that a circular doubly linked list contains three parts in its structure therefore, it demands more space per node and more expensive basic operations. However, a circular doubly linked list provides easy manipulation of the pointers and the searching becomes twice as efficient.
Memory Management of Circular Doubly linked list
The following figure shows the way in which the memory is allocated for a circular doubly linked list. The variable head contains the address of the first element of the list i.e. 1 hence the starting node of the list contains data A is stored at address 1. Since, each node of the list is supposed to have three parts therefore, the starting node of the list contains address of the last node i.e. 8 and the next node i.e. 4. The last node of the list that is stored at address 8 and containing data as 6, contains address of the first node of the list as shown in the image i.e. 1. In circular doubly linked list, the last node is identified by the address of the first node which is stored in the next part of the last node therefore the node which contains the address of the first node, is actually the last node of the list.
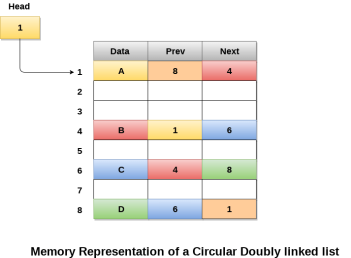
Operations on circular doubly linked list :
There are various operations which can be performed on circular doubly linked list. The node structure of a circular doubly linked list is similar to doubly linked list. However, the operations on circular doubly linked list is described in the following table.
SN | Operation | Description |
1 | Insertion at beginning | Adding a node in circular doubly linked list at the beginning. |
2 | Insertion at end | Adding a node in circular doubly linked list at the end. |
3 | Deletion at beginning | Removing a node in circular doubly linked list from beginning. |
4 | Deletion at end | Removing a node in circular doubly linked list at the end. |
Traversing and searching in circular doubly linked list is similar to that in the circular singly linked list.
C program to implement all the operations on circular doubly linked list
- #include<stdio.h>
- #include<stdlib.h>
- Struct node
- {
- Struct node *prev;
- Struct node *next;
- Int data;
- };
- Struct node *head;
- Void insertion_beginning();
- Void insertion_last();
- Void deletion_beginning();
- Void deletion_last();
- Void display();
- Void search();
- Void main ()
- {
- Int choice =0;
- While(choice != 9)
- {
- Printf("\n*********Main Menu*********\n");
- Printf("\nChoose one option from the following list ...\n");
- Printf("\n===============================================\n");
- Printf("\n1.Insert in Beginning\n2.Insert at last\n3.Delete from Beginning\n4.Delete from last\n5.Search\n6.Show\n7.Exit\n");
- Printf("\nEnter your choice?\n");
- Scanf("\n%d",&choice);
- Switch(choice)
- {
- Case 1:
- Insertion_beginning();
- Break;
- Case 2:
- Insertion_last();
- Break;
- Case 3:
- Deletion_beginning();
- Break;
- Case 4:
- Deletion_last();
- Break;
- Case 5:
- Search();
- Break;
- Case 6:
- Display();
- Break;
- Case 7:
- Exit(0);
- Break;
- Default:
- Printf("Please enter valid choice..");
- }
- }
- }
- Void insertion_beginning()
- {
- Struct node *ptr,*temp;
- Int item;
- Ptr = (struct node *)malloc(sizeof(struct node));
- If(ptr == NULL)
- {
- Printf("\nOVERFLOW");
- }
- Else
- {
- Printf("\nEnter Item value");
- Scanf("%d",&item);
- Ptr->data=item;
- If(head==NULL)
- {
- Head = ptr;
- Ptr -> next = head;
- Ptr -> prev = head;
- }
- Else
- {
- Temp = head;
- While(temp -> next != head)
- {
- Temp = temp -> next;
- }
- Temp -> next = ptr;
- Ptr -> prev = temp;
- Head -> prev = ptr;
- Ptr -> next = head;
- Head = ptr;
- }
- Printf("\nNode inserted\n");
- }
- }
- Void insertion_last()
- {
- Struct node *ptr,*temp;
- Int item;
- Ptr = (struct node *) malloc(sizeof(struct node));
- If(ptr == NULL)
- {
- Printf("\nOVERFLOW");
- }
- Else
- {
- Printf("\nEnter value");
- Scanf("%d",&item);
- Ptr->data=item;
- If(head == NULL)
- {
- Head = ptr;
- Ptr -> next = head;
- Ptr -> prev = head;
- }
- Else
- {
- Temp = head;
- While(temp->next !=head)
- {
- Temp = temp->next;
- }
- Temp->next = ptr;
- Ptr ->prev=temp;
- Head -> prev = ptr;
- Ptr -> next = head;
- }
- }
- Printf("\nnode inserted\n");
- }
- Void deletion_beginning()
- {
- Struct node *temp;
- If(head == NULL)
- {
- Printf("\n UNDERFLOW");
- }
- Else if(head->next == head)
- {
- Head = NULL;
- Free(head);
- Printf("\nnode deleted\n");
- }
- Else
- {
- Temp = head;
- While(temp -> next != head)
- {
- Temp = temp -> next;
- }
- Temp -> next = head -> next;
- Head -> next -> prev = temp;
- Free(head);
- Head = temp -> next;
- }
- }
- Void deletion_last()
- {
- Struct node *ptr;
- If(head == NULL)
- {
- Printf("\n UNDERFLOW");
- }
- Else if(head->next == head)
- {
- Head = NULL;
- Free(head);
- Printf("\nnode deleted\n");
- }
- Else
- {
- Ptr = head;
- If(ptr->next != head)
- {
- Ptr = ptr -> next;
- }
- Ptr -> prev -> next = head;
- Head -> prev = ptr -> prev;
- Free(ptr);
- Printf("\nnode deleted\n");
- }
- }
- Void display()
- {
- Struct node *ptr;
- Ptr=head;
- If(head == NULL)
- {
- Printf("\nnothing to print");
- }
- Else
- {
- Printf("\n printing values ... \n");
- While(ptr -> next != head)
- {
- Printf("%d\n", ptr -> data);
- Ptr = ptr -> next;
- }
- Printf("%d\n", ptr -> data);
- }
- }
- Void search()
- {
- Struct node *ptr;
- Int item,i=0,flag=1;
- Ptr = head;
- If(ptr == NULL)
- {
- Printf("\nEmpty List\n");
- }
- Else
- {
- Printf("\nEnter item which you want to search?\n");
- Scanf("%d",&item);
- If(head ->data == item)
- {
- Printf("item found at location %d",i+1);
- Flag=0;
- }
- Else
- {
- While (ptr->next != head)
- {
- If(ptr->data == item)
- {
- Printf("item found at location %d ",i+1);
- Flag=0;
- Break;
- }
- Else
- {
- Flag=1;
- }
- i++;
- Ptr = ptr -> next;
- }
- }
- If(flag != 0)
- {
- Printf("Item not found\n");
- }
- }
- }
Output:
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in Beginning
2.Insert at last
3.Delete from Beginning
4.Delete from last
5.Search
6.Show
7.Exit
Enter your choice?
1
Enter Item value123
Node inserted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in Beginning
2.Insert at last
3.Delete from Beginning
4.Delete from last
5.Search
6.Show
7.Exit
Enter your choice?
2
Enter value234
Node inserted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in Beginning
2.Insert at last
3.Delete from Beginning
4.Delete from last
5.Search
6.Show
7.Exit
Enter your choice?
1
Enter Item value90
Node inserted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in Beginning
2.Insert at last
3.Delete from Beginning
4.Delete from last
5.Search
6.Show
7.Exit
Enter your choice?
2
Enter value80
Node inserted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in Beginning
2.Insert at last
3.Delete from Beginning
4.Delete from last
5.Search
6.Show
7.Exit
Enter your choice?
3
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in Beginning
2.Insert at last
3.Delete from Beginning
4.Delete from last
5.Search
6.Show
7.Exit
Enter your choice?
4
Node deleted
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in Beginning
2.Insert at last
3.Delete from Beginning
4.Delete from last
5.Search
6.Show
7.Exit
Enter your choice?
6
Printing values ...
123
*********Main Menu*********
Choose one option from the following list ...
===============================================
1.Insert in Beginning
2.Insert at last
3.Delete from Beginning
4.Delete from last
5.Search
6.Show
7.Exit
Enter your choice?
5
Enter item which you want to search?
123
Item found at location 1
*********Main Menu*********
Choose one option from the following list ...
============================================
1.Insert in Beginning
2.Insert at last
3.Delete from Beginning
4.Delete from last
5.Search
6.Show
7.Exit
Enter your choice?
7
References:
1. G. A.V, PAI , “Data Structures and Algorithms “, McGraw Hill, ISBN -13: 978-0-07-066726-6
2. A. Tharp ,"File Organization and Processing", 2008 ,Willey India edition, 9788126518685
3. M. Folk, B. Zoellick, G. Riccardi, "File Structure An Object Oriented Approach with C++", Pearson Education, 2002, ISBN 81 - 7808 - 131 - 8.
4. M. Welss, “Data Structures and Algorithm Analysis in C++", 2nd edition, Pearson Education, 2002, ISBN81-7808-670-0