Unit 2
Searching and Sorting
Introduction to Searching
Searching in data structure refers to the process of finding location LOC of an element in a list. This is one of the important parts of many data structures algorithms, as one operation can be performed on an element if and only if we find it. Various algorithms have been defined to find whether an element is present in the collection of items or not. This algorithm can be executed on both internal as well as external data structures. The efficiency of searching an element increases the efficiency of any algorithm.
Searching Techniques in Data Structure
The most famous techniques of searching in data structures are:
1. Sequential Search
This is the traditional technique for searching an element in a collection of elements. In this type of search, all the elements of the list are traversed one by one to find if the element is present in the list or not. One example of such an algorithm is a linear search. This is a very simple and basic algorithm. Suppose ARR is an array of n elements, and we need to find location LOC of element ITEM in ARR. For this, LOC is assigned to -1 which indicates that ITEM is not present in ARR. While comparing ITEM with data at each location of ARR, and once ITEM == ARR[N], LOC is updated with location N+1. Hence we found the ITEM in ARR.
Algorithm:
LSEARCH(ARR, N, ITEM, LOC) Here ARR Is the array of N number of elements, ITEM holds the value we need to search in the array and algorithm returns LOC, the location where ITEM is present in the ARR. Initially, we have to set LOC = -1.
1. Set LOC = -1,i=1
2. Repeat while DATA[i] != ITEM:
i=i+1
3. If i=N+1 ,then Set LOC =0
Else LOC = N+1
4. Exit.
Let’s say, below is the ARR with 10 elements. And we need to find whether ITEM= 18 is present in this array or not.

In the start, LOC =-1
Step 1: ITEM != 77 thus we move to next element.
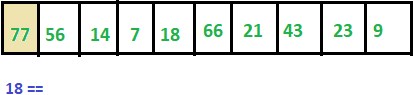
Step 2: ITEM != 56 thus we move to next element.
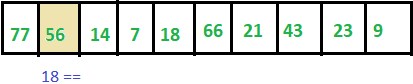
Step 3: ITEM != 14 thus we move to next element.
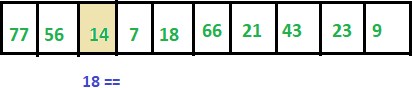
Step 4: ITEM != 7 thus we move to the next element.
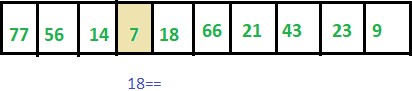
Step 5: Hence ITEM == ARR[4] thus LOC updated to 5.

Complexity of Sequential Search
Here are the complexities of the linear search given below.
Space complexity
As linear search algorithm does not use any extra space thus its space complexity = O(n) for an array of n number of elements.
Time Complexity
- Worst case complexity: O(n) – This case occurs when the element to search is not present in the array.
- Best case complexity: O(1) – This case occurs when the first element is the element to be searched.
- Average complexity: O(n) – This means when an element is present somewhere in the middle of the array.
2. Binary Search
This is a technique to search an element in the list using the divide and conquer technique. This type of technique is used in the case of sorted lists. Instead of searching an element one by one in the list, it directly goes to the middle element of the list and divides the array into 2 parts, and decides element lies in which sub-array does the element exist.
Suppose ARR is an array with sorted n number of elements present in increasing order. With every step of this algorithm, the searching is confined within BEG and END, which are the beginning and ending index of sub-arrays. The index MID defines the middle index of the array where,
MID = INT(beg + end )/2
And then, it needs to be checked if ITEM < ARR[N} where ITEM is the element that we need to search in ARR.
- If ITEM = ARR[MID] then LOC = MID and exit .
- If ITEM < ARR[MID} then ITEM can appear in the left sub-array, then BEG will be the same and END = MID -1 and repeat.
- If ITEM > ARR[MID] then ITEM can appear in the right subarray then BEG = MID+1 and END will be the same and repeat.
After this MID is again calculated for respective sub-arrays. In case we didn’t find the ITEM, the algorithm returns -1 otherwise LOC = MID.
Algorithm:
BSEARCH(ARR, LB, UB, ITEM, LOC) Here, ARR is a sorted list of elements, with LB and UB are lower and upper bounds for the array. ITEM needs to be searched in the array and algorithm returns location LOC, index at which ITEM is present else return -1.
1. Set BEG = LB, END = UB and MID = INT([BEG+END]/2)
2. Repeat step 3 and 4 while BEG <= END and ARR[MID] != ITEM
3. IF ITEM< ARR[MID] then:
Set END = MID-1
Else:
Set BEG = MID+1
4. Set MID = INT(BEG+END)/2
5. IF ARR[MID] = ITEM then:
Set LOC = MID
Else:
Set LOC = NULL
6. Exit.
Let’s say here, ITEM = 62

BEG = 1 and END =9 Hence MID = (1+9)/2 = 5
ARR[MID] = 52
Step 1: ARR[MID] < ITEM : thus END =9 and BEG = MID +1 = 6. Thus our new sub-array is,

Step 2: Now BEG =6 and END =9 thus MID = INT([6+9]/2)= 6
NOW ARR[6] =ITEM. Thus LOC = MID
Thus LOC = 6
Complexity of Binary Search
Here are the complexities of the binary search given below.
- Worst Case: O(nlogn)
- Best Case: O(1)
- Average Case: O(nlogn)
Conclusion
Searching refers to finding the location of one element in the array of n elements. There are 2 types of search linear and binary Search, Linear search algorithm is very simple and has O(n) of complexity whereas Binary Search is a very fast searching algorithm having the complexity of (logn) but can only be used in case of the sorted list of elements. In case the size of the array is large, it is preferable to use binary search instead of linear search. Binary search is used in many searching data structures. In the case of mid-size arrays, the linear search algorithm is more preferred.
Sorting Techniques
Sorting refers to arranging data in a particular format. Sorting algorithm specifies the way to arrange data in a particular order. Most common orders are in numerical or lexicographical order.
The importance of sorting lies in the fact that data searching can be optimized to a very high level, if data is stored in a sorted manner. Sorting is also used to represent data in more readable formats. Following are some of the examples of sorting in real-life scenarios −
- Telephone Directory − The telephone directory stores the telephone numbers of people sorted by their names, so that the names can be searched easily.
- Dictionary − The dictionary stores words in an alphabetical order so that searching of any word becomes easy.
In-place Sorting and Not-in-place Sorting
Sorting algorithms may require some extra space for comparison and temporary storage of few data elements. These algorithms do not require any extra space and sorting is said to happen in-place, or for example, within the array itself. This is called in-place sorting. Bubble sort is an example of in-place sorting.
However, in some sorting algorithms, the program requires space which is more than or equal to the elements being sorted. Sorting which uses equal or more space is called not-in-place sorting. Merge-sort is an example of not-in-place sorting.
Stable and Not Stable Sorting
If a sorting algorithm, after sorting the contents, does not change the sequence of similar content in which they appear, it is called stable sorting.
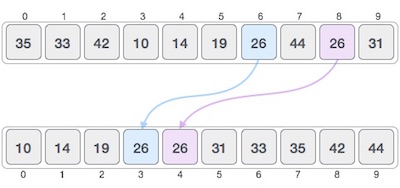
If a sorting algorithm, after sorting the contents, changes the sequence of similar content in which they appear, it is called unstable sorting.
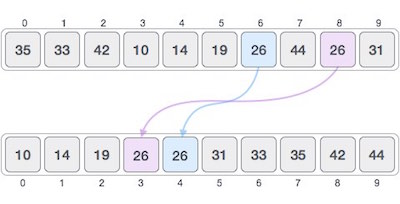
Stability of an algorithm matters when we wish to maintain the sequence of original elements, like in a tuple for example.
Adaptive and Non-Adaptive Sorting Algorithm
A sorting algorithm is said to be adaptive, if it takes advantage of already 'sorted' elements in the list that is to be sorted. That is, while sorting if the source list has some element already sorted, adaptive algorithms will take this into account and will try not to re-order them.
A non-adaptive algorithm is one which does not take into account the elements which are already sorted. They try to force every single element to be re-ordered to confirm their sortedness.
Important Terms
Some terms are generally coined while discussing sorting techniques, here is a brief introduction to them −
Increasing Order
A sequence of values is said to be in increasing order, if the successive element is greater than the previous one. For example, 1, 3, 4, 6, 8, 9 are in increasing order, as every next element is greater than the previous element.
Decreasing Order
A sequence of values is said to be in decreasing order, if the successive element is less than the current one. For example, 9, 8, 6, 4, 3, 1 are in decreasing order, as every next element is less than the previous element.
Non-Increasing Order
A sequence of values is said to be in non-increasing order, if the successive element is less than or equal to its previous element in the sequence. This order occurs when the sequence contains duplicate values. For example, 9, 8, 6, 3, 3, 1 are in non-increasing order, as every next element is less than or equal to (in case of 3) but not greater than any previous element.
Non-Decreasing Order
A sequence of values is said to be in non-decreasing order, if the successive element is greater than or equal to its previous element in the sequence. This order occurs when the sequence contains duplicate values. For example, 1, 3, 3, 6, 8, 9 are in non-decreasing order, as every next element is greater than or equal to (in case of 3) but not less than the previous one.
Sorting is a technique through which we arrange the data in such a manner so that the searching of the data becomes easy. A lot of sorting techniques has been implemented till now to cope up the faster execution of the result and to manage the data comfortably . Sorting and Searching are fundamental operations in computer science. Sorting refers to the operation of arranging data in some given order. Searching refers to the operation of searching the particular record from the existing information. Normally, the information retrieval involves searching, sorting and merging. In this chapter we will discuss the searching and sorting techniques in detail.Sorting is very important in every computer application. Sorting refers to arranging of data elements in some given order. Many Sorting algorithms are available to sort the given set of elements.
Let get to know about two sorting techniques and analyze their performance. The two techniques are:
Internal Sorting
External Sorting
Internal Sorting takes place in the main memory of a computer. The internal sorting methods are applied to small collection of data. It means that, the entire collection of data to be sorted in small enough that the sorting can take place within main memory. We will study the following methods of internal sorting
1. Insertion sort
2. Selection sort
3. Merge Sort
4. Radix Sort
5. Quick Sort
6. Heap Sort
7. Bubble Sort
Also a lot of algorithms are involved in sorting . Hence we should understand first that what is an algorithm .
Informally, an algorithm is any well-defined computational procedure that takes some value,
Or set of values, as input and produces some value, or set of values, as output. An algorithm is
Thus a sequence of computational steps that transform the input into the output.
We can also view an algorithm as a tool for solving a well-specified computational problem.
The statement of the problem specifies in general terms the desired input/output relationship.
The algorithm describes a specific computational procedure for achieving that input/output
Relationship.
For example, one might need to sort a sequence of numbers into non decreasing order. This
Problem arises frequently in practice and provides fertile ground for introducing many
Standard design techniques and analysis tools. Here is how we formally define the sorting problem.
Insertion Sort
This is a naturally occurring sorting method exemplified by a card player arranging the cards dealt to him. He picks up the cards as they are dealt and inserts them into the required position. Thus at every step, we insert an item into its proper place in an already ordered list.
We will illustrate insertion sort with an example (refer to Figure 10.1) before presenting the formal algorithm.
Sort the following list using the insertion sort method:
Thus to find the correct position search the list till an item just greater than the target is found. Shift all the items from this point one down the list. Insert the target in the vacated slot. Repeat this process for all the elements in the list. This results in sorted list.
Bubble Sort
In this sorting algorithm, multiple swappings take place in one pass. Smaller elements move or ‘bubble’ up to the top of the list, hence the name given to the algorithm.
In this method, adjacent members of the list to be sorted are compared.If the item on top is greater than the item immediately below it, then they are swapped. This process is carried on till the list is sorted.
The detailed algorithm follows:
Algorithm: BUBBLE SORT 6
1. Begin
2. Read the n elements
3. For i=1 to n
For j=n downto i+1
If a[j] <= a[j-1]
Swap(a[j],a[j-1])
4. End // of Bubble Sort
Total number of comparisons in Bubble sort :
= (N-1) +(N-2) . . . + 2 + 1
= (N-1)*N / 2 =O(N2)
This inefficiency is due to the fact that an item moves only to the next position in each pass.
Quick Sort
This is the most widely used internal sorting algorithm. In its basic form, it was invented by C.A.R. Hoare in 1960. Its popularity lies in the ease of implementation, moderate use of resources and acceptable behaviour for a variety of sorting cases. The basis of quick sort is the divide and conquer strategy i.e. Divide the problem [list to be sorted] into sub-problems [sub-lists], until solved sub problems [sorted sub-lists] are found. This is implemented as follows:
Choose one item A[I] from the list A[ ].
Rearrange the list so that this item is in the proper position, i.e., all preceding items have a lesser value and all succeeding items have a greater value than this item.
1. Place A[0], A[1] .. A[I-1] in sublist 1
2. A[I]
3. Place A[I + 1], A[I + 2] … A[N] in sublist 2
Repeat steps 1 & 2 for sublist1 & sublist2 till A[ ] is a sorted list.
As can be seen, this algorithm has a recursive structure.
The divide’ procedure is of utmost importance in this algorithm. This is usually implemented as follows:
1. Choose A[I] as the dividing element.
2. From the left end of the list (A[O] onwards) scan till an item A[R] is found whose value is greater than A[I].
3. From the right end of list [A[N] backwards] scan till an item A[L] is found whose value is less than A[1].
4. Swap A[R] & A[L].
5. Continue steps 2, 3 & 4 till the scan pointers cross. Stop at this stage.
6. At this point, sublist1 & sublist are ready.
7. Now do the same for each of sublist1 & sublist2.
C:UserssaurabhDesktopbubble-sort-3.pngC:UserssaurabhDesktopbubble_sort.jpg
EXTERNAL SORT GENERAL
Merging Lists Outline
1.Load the next sorted runs R1and R2into main memory buffers B1and B2 a page-at-a-time (i.e., initially first page from each run) (see left figure)
•Obviously R1>=B1 and R2>=B2 (a Run might be larger than a Buffer)
•The rest pages will be loaded to main memory during subsequent steps.
2.Initialize indices i, j to the head of each list (i.e., i=j=0)
3.Compare B1[i] with B2[j] and move smallest item to OUTPUT buffer.
•If B1[i] was smallest item then i++ else j++ (see right figure)
•If OUTPUT gets full, it is appended to the end of a file on DISK and cleared in RAM.
4.Repeat the above until either index i or j reaches the end of its buffer.
•At this point write the remaining records to OUTPUT, flush it to disk and finish.
5.Repeat procedure from 1-4 until all runs have been traversed.
A new sort algorithm, called AlphaSort, demonstrates that commodity processors and disks can handle commercial batch workloads. Using commodity processors, memory, and arrays of SCSI disks, AlphaSort runs the industry-standard sort benchmark in seven seconds. This beats the best published record on a 32-CPU 32-disk Hypercube by 8:1. On another benchmark, AlphaSort sorted more than a gigabyte in one minute. AlphaSort is a cache-sensitive, memory-intensive sort algorithm. We argue that modern architectures require algorithm designers to re-examine their use of the memory hierarchy. AlphaSort uses clustered data structures to get good cache locality, file striping to get high disk bandwidth, QuickSort to generate runs, and replacement-selection to merge the runs. It uses shared memory multiprocessors to break the sort into subsort chores. Because startup times are becoming a significant part of the total time, we propose two new benchmarks: (1) MinuteSort: how much can you sort in one minute, and (2) PennySort: how much can you sort for one penny.
Internal or External?
In an internal sort, the list of records is small enough to be maintained entirely in
Physical memory for the duration of the sort.
In an external sort, the list of records will not fit entirely into physical memory at once.
In that case, the records are kept in disk files and only a selection of them are resident
In physical memory at any given time.
The records stored in the list may be simple (e.g., string or int) or they may be
Complex structures. In any case, we will assume that:
– there is an implicit conversion of a record into its key value,
– key values may be compared using the usual relational operators (<, >, etc.).
The first assumption requires that the record type implementation provides an
Appropriate conversion operator.
The second assumption requires that the key type implementation provides an
Overloading of the relational operators.
None of these features are difficult for a client of the sortable list to implement, and the
Assumptions will make the implementation of the sortable list considerably simpler and
More elegant.
Sorting a list requires accessing the data elements stored in the list. For efficiency this
Suggests that the sort capability should be provided via member functions of the list
Class in question. We will follow that approach here, although the alternative is
Certainly feasible.
Building upon the LinkListT or ArrayT classes discussed earlier, we could derive
Sorted variants, overriding some member functions of the base class and adding new
Member functions for sorting.
If we do that, what base member functions must be overridden?
– The insertion functions must now take into account the ordering of the list
Elements, placing each new element in the proper location.
– A number of the base member functions are unsuitable for a sorted list type
And must be disabled.
– The search functions may now take advantage of the list element ordering.
Template class LinkListT {
Protected:
LinkNodeT* Head; // points to head node in list
LinkNodeT* Tail; // points to tail node in list
LinkNodeT* Curr; // points to “current” node in list
Public:
LinkListT();
LinkListT(const LinkListT& Source);
LinkListT& operator=(const LinkListT& Source);
~LinkListT();
Bool isEmpty() const;
Bool inList() const;
Bool PrefixNode(Item newData);
Bool AppendNode(Item newData);
Bool InsertAfterCurr(Item newData);
Bool Advance();
Void gotoHead();
Void gotoTail();
Bool MakeEmpty();
Bool DeleteCurrentNode();
Bool DeleteValue(Item Target);
Item getCurrentData() const;
Void PrintList(ostream& Out);
Inserting a new record into an ordered list requires:
– searching the list until the appropriate location is found
– creating an empty “slot” in the list to hold the new record
– placing the new record into that “slot”
The search phase is essentially trivial, aside from the issue of ties.
Naturally, a binary search should be used.
The creation of an empty “slot” depends upon the type of list:
– For a contiguous list, the tail of the list must be shifted to make room for the
New element.
– For a linked list, a new list node must be allocated and inserted.
Placing the record into the “slot” is trivial.
The approach described so far maintains the list in sorted order at all times, by placing
Each new element in the appropriate location when it is inserted to the list.
For a list containing N elements, whether contiguous or linked, the average cost of
Ordered insertion of a single new element is Θ(N). When an exact analysis is done,
Performance is worse, of course, for a contiguous list.
Greater efficiency can be obtained if the list elements are inserted and then an efficient
Sort algorithm is applied to the list.
Which approach is preferred depends upon how often the list receives insertions, and
Whether those insertions tend to be grouped or isolated (in time).
A sorting algorithm is said to be stable if two objects with equal keys appear in the same order in sorted output as they appear in the input unsorted array.
Some Sorting Algorithm is stable by nature like Insertion Sort, Merge Sort and Bubble Sort etc.
Sorting Algorithm is not stable like Quick Sort, Heap Sort etc.
Another Definition of Stable Sorting:
A Stable Sort is one which preserves the original order of input set, where the comparison algorithm does not distinguish between two or more items. A Stable Sort will guarantee that the original order of data having the same rank is preserved in the output.
In Place Sorting Algorithm:
- An In-Place Sorting Algorithm directly modifies the list that is received as input instead of creating a new list that is then modified.
- In this Sorting, a small amount of extra space it uses to manipulate the input set. In other Words, the output is placed in the correct position while the algorithm is still executing, which means that the input will be overwritten by the desired output on run-time.
- In-Place, Sorting Algorithm updates input only through replacement or swapping of elements.
- An algorithm which is not in-place is sometimes called not-in-Place or out of Place.
- An Algorithm can only have a constant amount of extra space, counting everything including function call and Pointers, Usually; this space is O (log n).
Note:
- Bubble sort, insertion sort, and selection sort are in-place sorting algorithms. Because only swapping of the element in the input array is required.
- Bubble sort and insertion sort can be applying as stable algorithms but selection sort cannot (without significant modifications).
- Merge sort is a stable algorithm but not an in-place algorithm. It requires extra array storage.
- Quicksort is not stable but is an in-place algorithm.
- Heap sort is an in-place algorithm but is not stable.
Searching
Searching is the process of finding some particular element in the list. If the element is present in the list, then the process is called successful and the process returns the location of that element, otherwise the search is called unsuccessful.
There are two popular search methods that are widely used in order to search some item into the list. However, choice of the algorithm depends upon the arrangement of the list.
- Linear Search
- Binary Search
Linear Search
Linear search is the simplest search algorithm and often called sequential search. In this type of searching, we simply traverse the list completely and match each element of the list with the item whose location is to be found. If the match found then location of the item is returned otherwise the algorithm return NULL.
Linear search is mostly used to search an unordered list in which the items are not sorted. The algorithm of linear search is given as follows.
Algorithm
- LINEAR_SEARCH(A, N, VAL)
- Step 1: [INITIALIZE] SET POS = -1
- Step 2: [INITIALIZE] SET I = 1
- Step 3: Repeat Step 4 while I<=N
- Step 4: IF A[I] = VAL
SET POS = I
PRINT POS
Go to Step 6
[END OF IF]
SET I = I + 1
[END OF LOOP] - Step 5: IF POS = -1
PRINT " VALUE IS NOT PRESENTIN THE ARRAY "
[END OF IF] - Step 6: EXIT
Complexity of algorithm
Complexity | Best Case | Average Case | Worst Case |
Time | O(1) | O(n) | O(n) |
Space |
|
| O(1) |
C Program
- #include<stdio.h>
- Void main ()
- {
- Int a[10] = {10, 23, 40, 1, 2, 0, 14, 13, 50, 9};
- Int item, i,flag;
- Printf("\nEnter Item which is to be searched\n");
- Scanf("%d",&item);
- For (i = 0; i< 10; i++)
- {
- If(a[i] == item)
- {
- Flag = i+1;
- Break;
- }
- Else
- Flag = 0;
- }
- If(flag != 0)
- {
- Printf("\nItem found at location %d\n",flag);
- }
- Else
- {
- Printf("\nItem not found\n");
- }
- }
Output:
Enter Item which is to be searched
20
Item not found
Enter Item which is to be searched
23
Item found at location 2
Java Program
- Import java.util.Scanner;
- Public class Leniear_Search {
- Public static void main(String[] args) {
- Int[] arr = {10, 23, 15, 8, 4, 3, 25, 30, 34, 2, 19};
- Int item,flag=0;
- Scanner sc = new Scanner(System.in);
- System.out.println("Enter Item ?");
- Item = sc.nextInt();
- For(int i = 0; i<10; i++)
- {
- If(arr[i]==item)
- {
- Flag = i+1;
- Break;
- }
- Else
- Flag = 0;
- }
- If(flag != 0)
- {
- System.out.println("Item found at location" + flag);
- }
- Else
- System.out.println("Item not found");
- }
- }
Output:
Enter Item ?
23
Item found at location 2
Enter Item ?
22
Item not found
C# Program
- Using System;
- Public class LinearSearch
- {
- Public static void Main()
- {
- Int item, flag = 0;
- Int[] a= {10, 23, 5, 90, 89, 34, 12, 34, 1, 78};
- Console.WriteLine("Enter the item value");
- Item = Convert.ToInt32(Console.ReadLine());
- For(int i=0;i<10;i++)
- {
- If(item == a[i])
- {
- Flag = i+1;
- Break;
- }
- Else
- Flag = 0;
- }
- If(flag != 0 )
- {
- Console.WriteLine("Item Found at Location " + flag);
- }
- Else
- Console.WriteLine("Item Not Found");
- }
- }
Output:
Enter the item value
78
Item Found at Location 10
Enter the item value
22
Item not found
Python Program
- Arr = [10,2,3,4,23,5,21,45,90,100];
- Item = int(input("Enter the item which you want to search "));
- For i in range (0,len(arr)):
- If arr[i] == item:
- Flag = i+1;
- Break;
- Else:
- Flag = 0;
- If flag != 0:
- Print("Item found at location %d" % (flag));
- Else :
- Print("Item not found");
Output:
Enter the item which you want to search 2
Item found at location 2
Enter the item which you want to search 101
Item not found
Binary Search
Binary search is the search technique which works efficiently on the sorted lists. Hence, in order to search an element into some list by using binary search technique, we must ensure that the list is sorted.
Binary search follows divide and conquer approach in which, the list is divided into two halves and the item is compared with the middle element of the list. If the match is found then, the location of middle element is returned otherwise, we search into either of the halves depending upon the result produced through the match.
Binary search algorithm is given below.
BINARY_SEARCH(A, lower_bound, upper_bound, VAL)
- Step 1: [INITIALIZE] SET BEG = lower_bound
END = upper_bound, POS = - 1 - Step 2: Repeat Steps 3 and 4 while BEG <=END
- Step 3: SET MID = (BEG + END)/2
- Step 4: IF A[MID] = VAL
SET POS = MID
PRINT POS
Go to Step 6
ELSE IF A[MID] > VAL
SET END = MID - 1
ELSE
SET BEG = MID + 1
[END OF IF]
[END OF LOOP] - Step 5: IF POS = -1
PRINT "VALUE IS NOT PRESENT IN THE ARRAY"
[END OF IF] - Step 6: EXIT
Complexity
SN | Performance | Complexity |
1 | Worst case | O(log n) |
2 | Best case | O(1) |
3 | Average Case | O(log n) |
4 | Worst case space complexity | O(1) |
Example
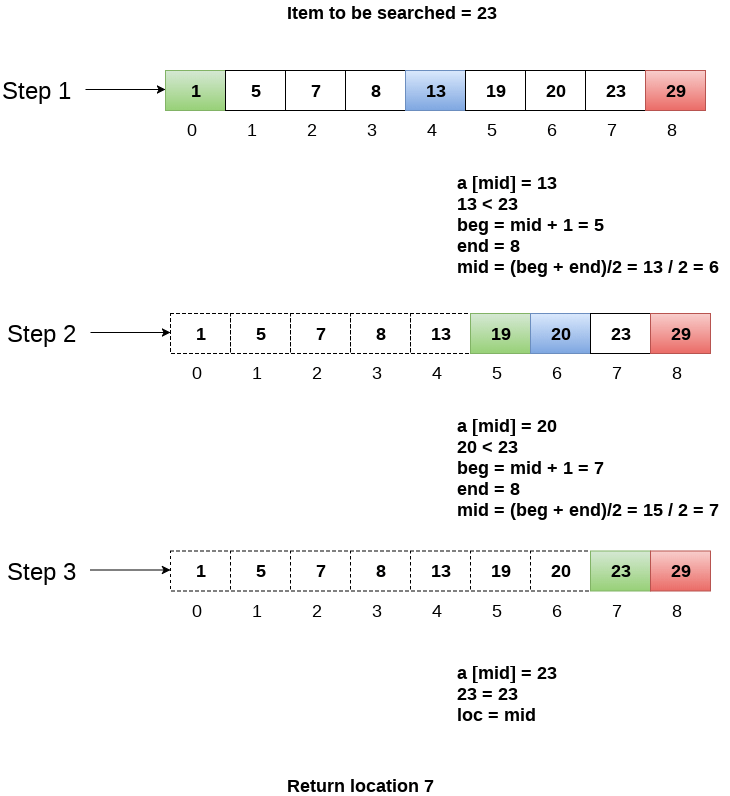
Let us consider an array arr = {1, 5, 7, 8, 13, 19, 20, 23, 29}. Find the location of the item 23 in the array.
In 1st step :
- BEG = 0
- END = 8ron
- MID = 4
- a[mid] = a[4] = 13 < 23, therefore
In Second step:
- Beg = mid +1 = 5
- End = 8
- Mid = 13/2 = 6
- a[mid] = a[6] = 20 < 23, therefore;
In third step:
- Beg = mid + 1 = 7
- End = 8
- Mid = 15/2 = 7
- a[mid] = a[7]
- a[7] = 23 = item;
- Therefore, set location = mid;
- The location of the item will be 7.
Binary Search Program using Recursion
C program
- #include<stdio.h>
- Int binarySearch(int[], int, int, int);
- Void main ()
- {
- Int arr[10] = {16, 19, 20, 23, 45, 56, 78, 90, 96, 100};
- Int item, location=-1;
- Printf("Enter the item which you want to search ");
- Scanf("%d",&item);
- Location = binarySearch(arr, 0, 9, item);
- If(location != -1)
- {
- Printf("Item found at location %d",location);
- }
- Else
- {
- Printf("Item not found");
- }
- }
- Int binarySearch(int a[], int beg, int end, int item)
- {
- Int mid;
- If(end >= beg)
- {
- Mid = (beg + end)/2;
- If(a[mid] == item)
- {
- Return mid+1;
- }
- Else if(a[mid] < item)
- {
- Return binarySearch(a,mid+1,end,item);
- }
- Else
- {
- Return binarySearch(a,beg,mid-1,item);
- }
- }
- Return -1;
- }
Output:
Enter the item which you want to search
19
Item found at location 2
Java
- Import java.util.*;
- Public class BinarySearch {
- Public static void main(String[] args) {
- Int[] arr = {16, 19, 20, 23, 45, 56, 78, 90, 96, 100};
- Int item, location = -1;
- System.out.println("Enter the item which you want to search");
- Scanner sc = new Scanner(System.in);
- Item = sc.nextInt();
- Location = binarySearch(arr,0,9,item);
- If(location != -1)
- System.out.println("the location of the item is "+location);
- Else
- System.out.println("Item not found");
- }
- Public static int binarySearch(int[] a, int beg, int end, int item)
- {
- Int mid;
- If(end >= beg)
- {
- Mid = (beg + end)/2;
- If(a[mid] == item)
- {
- Return mid+1;
- }
- Else if(a[mid] < item)
- {
- Return binarySearch(a,mid+1,end,item);
- }
- Else
- {
- Return binarySearch(a,beg,mid-1,item);
- }
- }
- Return -1;
- }
- }
Output:
Enter the item which you want to search
45
The location of the item is 5
C#
- Using System;
- Public class LinearSearch
- {
- Public static void Main()
- {
- Int[] arr = {16, 19, 20, 23, 45, 56, 78, 90, 96, 100};
- Int location=-1;
- Console.WriteLine("Enter the item which you want to search ");
- Int item = Convert.ToInt32(Console.ReadLine());
- Location = binarySearch(arr, 0, 9, item);
- If(location != -1)
- {
- Console.WriteLine("Item found at location "+ location);
- }
- Else
- {
- Console.WriteLine("Item not found");
- }
- }
- Public static int binarySearch(int[] a, int beg, int end, int item)
- {
- Int mid;
- If(end >= beg)
- {
- Mid = (beg + end)/2;
- If(a[mid] == item)
- {
- Return mid+1;
- }
- Else if(a[mid] < item)
- {
- Return binarySearch(a,mid+1,end,item);
- }
- Else
- {
- Return binarySearch(a,beg,mid-1,item);
- }
- }
- Return -1;
- }
- }
Output:
Enter the item which you want to search
20
Item found at location 3
Python
- Def binarySearch(arr,beg,end,item):
- If end >= beg:
- Mid = int((beg+end)/2)
- If arr[mid] == item :
- Return mid+1
- Elif arr[mid] < item :
- Return binarySearch(arr,mid+1,end,item)
- Else:
- Return binarySearch(arr,beg,mid-1,item)
- Return -1
- Arr=[16, 19, 20, 23, 45, 56, 78, 90, 96, 100];
- Item = int(input("Enter the item which you want to search ?"))
- Location = -1;
- Location = binarySearch(arr,0,9,item);
- If location != -1:
- Print("Item found at location %d" %(location))
- Else:
- Print("Item not found")
Output:
Enter the item which you want to search ?
96
Item found at location 9
Enter the item which you want to search ?
101
Item not found
Binary Search function using Iteration
- Int binarySearch(int a[], int beg, int end, int item)
- {
- Int mid;
- While(end >= beg)
- {
- Mid = (beg + end)/2;
- If(a[mid] == item)
- {
- Return mid+1;
- }
- Else if(a[mid] < item)
- {
- Beg = mid + 1;
- }
- Else
- {
- End = mid - 1;
- }
- }
- Return -1;
- }
Fibonacci Series
Fibonacci series generates the subsequent number by adding two previous numbers. Fibonacci series starts from two numbers − F0 & F1. The initial values of F0 & F1 can be taken 0, 1 or 1, 1 respectively.
Fibonacci series satisfies the following conditions −
Fn = Fn-1 + Fn-2
Hence, a Fibonacci series can look like this −
F8 = 0 1 1 2 3 5 8 13
Or, this −
F8 = 1 1 2 3 5 8 13 21
For illustration purpose, Fibonacci of F8 is displayed as −
Fibonacci Iterative Algorithm
First we try to draft the iterative algorithm for Fibonacci series.
Procedure Fibonacci(n)
Declare f0, f1, fib, loop
Set f0 to 0
Set f1 to 1
Display f0, f1
For loop ← 1 to n
Fib ← f0 + f1
f0 ← f1
f1 ← fib
Display fib
End for
End procedure
Fibonacci Recursive Algorithm
Let us learn how to create a recursive algorithm Fibonacci series. The base criteria of recursion.
START
Procedure Fibonacci(n)
Declare f0, f1, fib, loop
Set f0 to 0
Set f1 to 1
Display f0, f1
For loop ← 1 to n
Fib ← f0 + f1
f0 ← f1
f1 ← fib
Display fib
End for
END
Bubble Sort
In Bubble sort, Each element of the array is compared with its adjacent element. The algorithm processes the list in passes. A list with n elements requires n-1 passes for sorting. Consider an array A of n elements whose elements are to be sorted by using Bubble sort. The algorithm processes like following.
- In Pass 1, A[0] is compared with A[1], A[1] is compared with A[2], A[2] is compared with A[3] and so on. At the end of pass 1, the largest element of the list is placed at the highest index of the list.
- In Pass 2, A[0] is compared with A[1], A[1] is compared with A[2] and so on. At the end of Pass 2 the second largest element of the list is placed at the second highest index of the list.
- In pass n-1, A[0] is compared with A[1], A[1] is compared with A[2] and so on. At the end of this pass. The smallest element of the list is placed at the first index of the list.
Algorithm :
- Step 1: Repeat Step 2 For i = 0 to N-1
- Step 2: Repeat For J = i + 1 to N - I
- Step 3: IF A[J] > A[i]
SWAP A[J] and A[i]
[END OF INNER LOOP]
[END OF OUTER LOOP - Step 4: EXIT
Complexity
Scenario | Complexity |
Space | O(1) |
Worst case running time | O(n2) |
Average case running time | O(n) |
Best case running time | O(n2) |
C Program
- #include<stdio.h>
- Void main ()
- {
- Int i, j,temp;
- Int a[10] = { 10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
- For(i = 0; i<10; i++)
- {
- For(j = i+1; j<10; j++)
- {
- If(a[j] > a[i])
- {
- Temp = a[i];
- a[i] = a[j];
- a[j] = temp;
- }
- }
- }
- Printf("Printing Sorted Element List ...\n");
- For(i = 0; i<10; i++)
- {
- Printf("%d\n",a[i]);
- }
- }
Output:
Printing Sorted Element List . . .
7
9
10
12
23
34
34
44
78
101
C++ Program
- #include<iostream>
- Using namespace std;
- Int main ()
- {
- Int i, j,temp;
- Int a[10] = { 10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
- For(i = 0; i<10; i++)
- {
- For(j = i+1; j<10; j++)
- {
- If(a[j] < a[i])
- {
- Temp = a[i];
- a[i] = a[j];
- a[j] = temp;
- }
- }
- }
- Cout <<"Printing Sorted Element List ...\n";
- For(i = 0; i<10; i++)
- {
- Cout <<a[i]<<"\n";
- }
- Return 0;
- }
Output:
Printing Sorted Element List ...
7
9
10
12
23
23
34
44
78
101
Java Program
- Public class BubbleSort {
- Public static void main(String[] args) {
- Int[] a = {10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
- For(int i=0;i<10;i++)
- {
- For (int j=0;j<10;j++)
- {
- If(a[i]<a[j])
- {
- Int temp = a[i];
- a[i]=a[j];
- a[j] = temp;
- }
- }
- }
- System.out.println("Printing Sorted List ...");
- For(int i=0;i<10;i++)
- {
- System.out.println(a[i]);
- }
- }
- }
Output:
Printing Sorted List . . .
7
9
10
12
23
34
34
44
78
101
C# Program
- Using System;
- Public class Program
- {
- Public static void Main()
- {
- Int i, j,temp;
- Int[] a = {10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
- For(i = 0; i<10; i++)
- {
- For(j = i+1; j<10; j++)
- {
- If(a[j] > a[i])
- {
- Temp = a[i];
- a[i] = a[j];
- a[j] = temp;
- }
- }
- }
- Console.WriteLine("Printing Sorted Element List ...\n");
- For(i = 0; i<10; i++)
- {
- Console.WriteLine(a[i]);
- }
- }
- }
Output:
Printing Sorted Element List . . .
7
9
10
12
23
34
34
44
78
101
Python Program
- a=[10, 9, 7, 101, 23, 44, 12, 78, 34, 23]
- For i in range(0,len(a)):
- For j in range(i+1,len(a)):
- If a[j]<a[i]:
- Temp = a[j]
- a[j]=a[i]
- a[i]=temp
- Print("Printing Sorted Element List...")
- For i in a:
- Print(i)
Output:
Printing Sorted Element List . . .
7
9
10
12
23
34
34
44
78
101
Rust Program
- Fn main()
- {
- Let mut temp;
- Let mut a: [i32; 10] = [10, 9, 7, 101, 23, 44, 12, 78, 34, 23];
- For i in 0..10
- {
- For j in (i+1)..10
- {
- If a[j] < a[i]
- {
- Temp = a[i];
- a[i] = a[j];
- a[j] = temp;
- }
- }
- }
- Println!("Printing Sorted Element List ...\n");
- For i in &a
- {
- Println!("{} ",i);
- }
- }
Output:
Printing Sorted Element List . . .
7
9
10
12
23
34
34
44
78
101
4
JavaScript Program
- <html>
- <head>
- <title>
- Bubble Sort
- </title>
- </head>
- <body>
- <script>
- Var a = [10, 9, 7, 101, 23, 44, 12, 78, 34, 23];
- For(i=0;i<10;i++)
- {
- For (j=0;j<10;j++)
- {
- If(a[i]<a[j])
- {
- Temp = a[i];
- a[i]=a[j];
- a[j] = temp;
- }
- }
- }
- Txt = "<br>";
- Document.writeln("Printing Sorted Element List ..."+txt);
- For(i=0;i<10;i++)
- {
- Document.writeln(a[i]);
- Document.writeln(txt);
- }
- </script>
- </body>
- </html>
Output:
Printing Sorted Element List ...
7
9
10
12
23
23
34
44
78
101
PHP Program
- <html>
- <head>
- <title>Bubble Sort</title>
- </head>
- <body>
- <?php
- $a = array(10, 9, 7, 101, 23, 44, 12, 78, 34, 23);
- For($i=0;$i<10;$i++)
- {
- For ($j=0;$j<10;$j++)
- {
- If($a[$i]<$a[$j])
- {
- $temp = $a[$i];
- $a[$i]=$a[$j];
- $a[$j] = $temp;
- }
- }
- }
- Echo "Printing Sorted Element List ...\n";
- For($i=0;$i<10;$i++)
- {
- Echo $a[$i];
- Echo "\n";
- }
- ?>
- </body>
- </html>
Output:
Printing Sorted Element List ...
7
9
10
12
23
23
34
44
78
101
Insertion Sort
Insertion sort is the simple sorting algorithm which is commonly used in the daily lives while ordering a deck of cards. In this algorithm, we insert each element onto its proper place in the sorted array. This is less efficient than the other sort algorithms like quick sort, merge sort, etc.
Technique
Consider an array A whose elements are to be sorted. Initially, A[0] is the only element on the sorted set. In pass 1, A[1] is placed at its proper index in the array.
In pass 2, A[2] is placed at its proper index in the array. Likewise, in pass n-1, A[n-1] is placed at its proper index into the array.
To insert an element A[k] to its proper index, we must compare it with all other elements i.e. A[k-1], A[k-2], and so on until we find an element A[j] such that, A[j]<=A[k].
All the elements from A[k-1] to A[j] need to be shifted and A[k] will be moved to A[j+1].
Complexity
Complexity | Best Case | Average Case | Worst Case |
Time | Ω(n) | θ(n2) | o(n2) |
Space |
|
| o(1) |
Algorithm
- Step 1: Repeat Steps 2 to 5 for K = 1 to N-1
- Step 2: SET TEMP = ARR[K]
- Step 3: SET J = K - 1
- Step 4: Repeat while TEMP <=ARR[J]
SET ARR[J + 1] = ARR[J]
SET J = J - 1
[END OF INNER LOOP] - Step 5: SET ARR[J + 1] = TEMP
[END OF LOOP] - Step 6: EXIT
C Program
- #include<stdio.h>
- Void main ()
- {
- Int i,j, k,temp;
- Int a[10] = { 10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
- Printf("\nprinting sorted elements...\n");
- For(k=1; k<10; k++)
- {
- Temp = a[k];
- j= k-1;
- While(j>=0 && temp <= a[j])
- {
- a[j+1] = a[j];
- j = j-1;
- }
- a[j+1] = temp;
- }
- For(i=0;i<10;i++)
- {
- Printf("\n%d\n",a[i]);
- }
- }
Output:
Printing Sorted Elements . . .
7
9
10
12
23
23
34
44
78
101
C++ Program
- #include<iostream>
- Using namespace std;
- Int main ()
- {
- Int i,j, k,temp;
- Int a[10] = { 10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
- Cout<<"\nprinting sorted elements...\n";
- For(k=1; k<10; k++)
- {
- Temp = a[k];
- j= k-1;
- While(j>=0 && temp <= a[j])
- {
- a[j+1] = a[j];
- j = j-1;
- }
- a[j+1] = temp;
- }
- For(i=0;i<10;i++)
- {
- Cout <<a[i]<<"\n";
- }
- }
Output:
Printing sorted elements...
7
9
10
12
23
23
34
44
78
101
Java Program
- Public class InsertionSort {
- Public static void main(String[] args) {
- Int[] a = {10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
- For(int k=1; k<10; k++)
- {
- Int temp = a[k];
- Int j= k-1;
- While(j>=0 && temp <= a[j])
- {
- a[j+1] = a[j];
- j = j-1;
- }
- a[j+1] = temp;
- }
- System.out.println("printing sorted elements ...");
- For(int i=0;i<10;i++)
- {
- System.out.println(a[i]);
- }
- }
- }
Output:
Printing sorted elements . . .
7
9
10
12
23
23
34
44
78
101
C# Program
- Using System;
- Public class Program
- {
- Public static void Main()
- {
- Int i,j, k,temp;
- Int[] a = { 10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
- Console.WriteLine("\nprinting sorted elements...\n");
- For(k=1; k<10; k++)
- {
- Temp = a[k];
- j= k-1;
- While(j>=0 && temp <= a[j])
- {
- a[j+1] = a[j];
- j = j-1;
- }
- a[j+1] = temp;
- }
- For(i=0;i<10;i++)
- {
- Console.WriteLine(a[i]);
- }
- }
- }
Output:
Printing sorted elements . . .
7
9
10
12
23
23
34
44
78
101
Python Program
- a=[10, 9, 7, 101, 23, 44, 12, 78, 34, 23]
- For k in range(1,10):
- Temp = a[k]
- j = k-1
- While j>=0 and temp <=a[j]:
- a[j+1]=a[j]
- j = j-1
- a[j+1] = temp
- Print("printing sorted elements...")
- For i in a:
- Print(i)
Output:
Printing sorted elements . . .
7
9
10
12
23
23
34
44
78
101
Swift Program
- Import Foundation
- Import Glibc
- Var a = [10, 9, 7, 101, 23, 44, 12, 78, 34, 23];
- Print("\nprinting sorted elements...\n");
- For k in 1...9
- {
- Let temp = a[k];
- Var j = k-1;
- While j>=0 && temp <= a[j]
- {
- a[j+1] = a[j];
- j = j-1;
- }
- a[j+1] = temp;
- }
- For i in a
- {
- Print(i);
- }
Output:
Printing sorted elements...
7
9
10
12
23
23
34
44
78
101
JavaScript Program
- <html>
- <head>
- <title>
- Insertion Sort
- </title>
- </head>
- <body>
- <script>
- Var txt = "<br>";
- Var a = [10, 9, 7, 101, 23, 44, 12, 78, 34, 23];
- Document.writeln("printing sorted elements ... "+txt);
- For(k=0;k<10;k++)
- {
- Var temp = a[k]
- j=k-1;
- While (j>=0 && temp <= a[j])
- {
- a[j+1] = a[j];
- jj = j-1;
- }
- a[j+1] = temp;
- }
- For(i=0;i<10;i++)
- {
- Document.writeln(a[i]);
- Document.writeln(txt);
- }
- </script>
- </body>
- </html>
Output:
Printing sorted elements ...
7
9
10
12
23
23
34
44
78
101
PHP Program
- <html>
- <head>
- <title>Insertion Sort</title>
- </head>
- <body>
- <?php
- $a = array(10, 9, 7, 101, 23, 44, 12, 78, 34, 23);
- Echo("printing sorted elements ... \n");
- For($k=0;$k<10;$k++)
- {
- $temp = $a[$k];
- $j=$k-1;
- While ($j>=0 && $temp <= $a[$j])
- {
- $a[$j+1] = $a[$j];
- $j = $j-1;
- }
- $a[$j+1] = $temp;
- }
- For($i=0;$i<10;$i++)
- {
- Echo $a[$i];
- Echo "\n";
- }
- ?>
- </body>
- </html>
Output:
Printing sorted elements ...
7
9
10
12
23
23
34
44
78
101
Quick Sort
Quick sort is the widely used sorting algorithm that makes n log n comparisons in average case for sorting of an array of n elements. This algorithm follows divide and conquer approach. The algorithm processes the array in the following way.
- Set the first index of the array to left and loc variable. Set the last index of the array to right variable. i.e. left = 0, loc = 0, en d = n - 1, where n is the length of the array.
- Start from the right of the array and scan the complete array from right to beginning comparing each element of the array with the element pointed by loc.
Ensure that, a[loc] is less than a[right].
- If this is the case, then continue with the comparison until right becomes equal to the loc.
- If a[loc] > a[right], then swap the two values. And go to step 3.
- Set, loc = right
- Start from element pointed by left and compare each element in its way with the element pointed by the variable loc. Ensure that a[loc] > a[left]
- If this is the case, then continue with the comparison until loc becomes equal to left.
- [loc] < a[right], then swap the two values and go to step 2.
- Set, loc = left.
Complexity
Complexity | Best Case | Average Case | Worst Case |
Time Complexity | O(n) for 3 way partition or O(n log n) simple partition | O(n log n) | O(n2) |
Space Complexity |
|
| O(log n) |
Algorithm
PARTITION (ARR, BEG, END, LOC)
- Step 1: [INITIALIZE] SET LEFT = BEG, RIGHT = END, LOC = BEG, FLAG =
- Step 2: Repeat Steps 3 to 6 while FLAG =
- Step 3: Repeat while ARR[LOC] <=ARR[RIGHT]
AND LOC != RIGHT
SET RIGHT = RIGHT - 1
[END OF LOOP] - Step 4: IF LOC = RIGHT
SET FLAG = 1
ELSE IF ARR[LOC] > ARR[RIGHT]
SWAP ARR[LOC] with ARR[RIGHT]
SET LOC = RIGHT
[END OF IF] - Step 5: IF FLAG = 0
Repeat while ARR[LOC] >= ARR[LEFT] AND LOC != LEFT
SET LEFT = LEFT + 1
[END OF LOOP] - Step 6:IF LOC = LEFT
SET FLAG = 1
ELSE IF ARR[LOC] < ARR[LEFT]
SWAP ARR[LOC] with ARR[LEFT]
SET LOC = LEFT
[END OF IF]
[END OF IF] - Step 7: [END OF LOOP]
- Step 8: END
QUICK_SORT (ARR, BEG, END)
- Step 1: IF (BEG < END)
CALL PARTITION (ARR, BEG, END, LOC)
CALL QUICKSORT(ARR, BEG, LOC - 1)
CALL QUICKSORT(ARR, LOC + 1, END)
[END OF IF] - Step 2: END
C Program
- #include <stdio.h>
- Int partition(int a[], int beg, int end);
- Void quickSort(int a[], int beg, int end);
- Void main()
- {
- Int i;
- Int arr[10]={90,23,101,45,65,23,67,89,34,23};
- QuickSort(arr, 0, 9);
- Printf("\n The sorted array is: \n");
- For(i=0;i<10;i++)
- Printf(" %d\t", arr[i]);
- }
- Int partition(int a[], int beg, int end)
- {
- Int left, right, temp, loc, flag;
- Loc = left = beg;
- Right = end;
- Flag = 0;
- While(flag != 1)
- {
- While((a[loc] <= a[right]) && (loc!=right))
- Right--;
- If(loc==right)
- Flag =1;
- Else if(a[loc]>a[right])
- {
- Temp = a[loc];
- a[loc] = a[right];
- a[right] = temp;
- Loc = right;
- }
- If(flag!=1)
- {
- While((a[loc] >= a[left]) && (loc!=left))
- Left++;
- If(loc==left)
- Flag =1;
- Else if(a[loc] <a[left])
- {
- Temp = a[loc];
- a[loc] = a[left];
- a[left] = temp;
- Loc = left;
- }
- }
- }
- Return loc;
- }
- Void quickSort(int a[], int beg, int end)
- {
- Int loc;
- If(beg<end)
- {
- Loc = partition(a, beg, end);
- QuickSort(a, beg, loc-1);
- QuickSort(a, loc+1, end);
- }
- }
Output:
The sorted array is:
23
23
23
34
45
65
67
89
90
101
Java Program
- Public class QuickSort {
- Public static void main(String[] args) {
- Int i;
- Int[] arr={90,23,101,45,65,23,67,89,34,23};
- QuickSort(arr, 0, 9);
- System.out.println("\n The sorted array is: \n");
- For(i=0;i<10;i++)
- System.out.println(arr[i]);
- }
- Public static int partition(int a[], int beg, int end)
- {
- Int left, right, temp, loc, flag;
- Loc = left = beg;
- Right = end;
- Flag = 0;
- While(flag != 1)
- {
- While((a[loc] <= a[right]) && (loc!=right))
- Right--;
- If(loc==right)
- Flag =1;
- Elseif(a[loc]>a[right])
- {
- Temp = a[loc];
- a[loc] = a[right];
- a[right] = temp;
- Loc = right;
- }
- If(flag!=1)
- {
- While((a[loc] >= a[left]) && (loc!=left))
- Left++;
- If(loc==left)
- Flag =1;
- Elseif(a[loc] <a[left])
- {
- Temp = a[loc];
- a[loc] = a[left];
- a[left] = temp;
- Loc = left;
- }
- }
- }
- Returnloc;
- }
- Static void quickSort(int a[], int beg, int end)
- {
- Int loc;
- If(beg<end)
- {
- Loc = partition(a, beg, end);
- QuickSort(a, beg, loc-1);
- QuickSort(a, loc+1, end);
- }
- }
- }
Output:
The sorted array is:
23
23
23
34
45
65
67
89
90
101
C# Program
- Using System;
- Public class QueueSort{
- Public static void Main() {
- Int i;
- Int[] arr={90,23,101,45,65,23,67,89,34,23};
- QuickSort(arr, 0, 9);
- Console.WriteLine("\n The sorted array is: \n");
- For(i=0;i<10;i++)
- Console.WriteLine(arr[i]);
- }
- Public static int partition(int[] a, int beg, int end)
- {
- Int left, right, temp, loc, flag;
- Loc = left = beg;
- Right = end;
- Flag = 0;
- While(flag != 1)
- {
- While((a[loc] <= a[right]) && (loc!=right))
- Right--;
- If(loc==right)
- Flag =1;
- Else if(a[loc]>a[right])
- {
- Temp = a[loc];
- a[loc] = a[right];
- a[right] = temp;
- Loc = right;
- }
- If(flag!=1)
- {
- While((a[loc] >= a[left]) && (loc!=left))
- Left++;
- If(loc==left)
- Flag =1;
- Else if(a[loc] <a[left])
- {
- Temp = a[loc];
- a[loc] = a[left];
- a[left] = temp;
- Loc = left;
- }
- }
- }
- Return loc;
- }
- Static void quickSort(int[] a, int beg, int end)
- {
- Int loc;
- If(beg<end)
- {
- Loc = partition(a, beg, end);
- QuickSort(a, beg, loc-1);
- QuickSort(a, loc+1, end);
- }
- }
- }
Output:
The sorted array is:
23
23
23
34
45
65
67
89
90
101
Merge sort
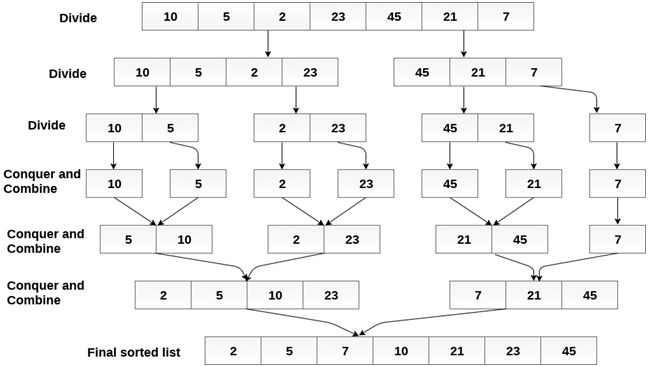
Merge sort is the algorithm which follows divide and conquer approach. Consider an array A of n number of elements. The algorithm processes the elements in 3 steps.
- If A Contains 0 or 1 elements then it is already sorted, otherwise, Divide A into two sub-array of equal number of elements.
- Conquer means sort the two sub-arrays recursively using the merge sort.
- Combine the sub-arrays to form a single final sorted array maintaining the ordering of the array.
The main idea behind merge sort is that, the short list takes less time to be sorted.
Complexity
Complexity | Best case | Average Case | Worst Case |
Time Complexity | O(n log n) | O(n log n) | O(n log n) |
Space Complexity |
|
| O(n) |
Example :
Consider the following array of 7 elements. Sort the array by using merge sort.
- A = {10, 5, 2, 23, 45, 21, 7}
Algorithm
- Step 1: [INITIALIZE] SET I = BEG, J = MID + 1, INDEX = 0
- Step 2: Repeat while (I <= MID) AND (J<=END)
IF ARR[I] < ARR[J]
SET TEMP[INDEX] = ARR[I]
SET I = I + 1
ELSE
SET TEMP[INDEX] = ARR[J]
SET J = J + 1
[END OF IF]
SET INDEX = INDEX + 1
[END OF LOOP]
Step 3: [Copy the remaining
elements of right sub-array, if
any]
IF I > MID
Repeat while J <= END
SET TEMP[INDEX] = ARR[J]
SET INDEX = INDEX + 1, SET J = J + 1
[END OF LOOP]
[Copy the remaining elements of
left sub-array, if any]
ELSE
Repeat while I <= MID
SET TEMP[INDEX] = ARR[I]
SET INDEX = INDEX + 1, SET I = I + 1
[END OF LOOP]
[END OF IF] - Step 4: [Copy the contents of TEMP back to ARR] SET K = 0
- Step 5: Repeat while K < INDEX
SET ARR[K] = TEMP[K]
SET K = K + 1
[END OF LOOP] - Step 6: Exit
MERGE_SORT(ARR, BEG, END)
- Step 1: IF BEG < END
SET MID = (BEG + END)/2
CALL MERGE_SORT (ARR, BEG, MID)
CALL MERGE_SORT (ARR, MID + 1, END)
MERGE (ARR, BEG, MID, END)
[END OF IF] - Step 2: END
C Program
- #include<stdio.h>
- Void mergeSort(int[],int,int);
- Void merge(int[],int,int,int);
- Void main ()
- {
- Int a[10]= {10, 9, 7, 101, 23, 44, 12, 78, 34, 23};
- Int i;
- MergeSort(a,0,9);
- Printf("printing the sorted elements");
- For(i=0;i<10;i++)
- {
- Printf("\n%d\n",a[i]);
- }
- }
- Void mergeSort(int a[], int beg, int end)
- {
- Int mid;
- If(beg<end)
- {
- Mid = (beg+end)/2;
- MergeSort(a,beg,mid);
- MergeSort(a,mid+1,end);
- Merge(a,beg,mid,end);
- }
- }
- Void merge(int a[], int beg, int mid, int end)
- {
- Int i=beg,j=mid+1,k,index = beg;
- Int temp[10];
- While(i<=mid && j<=end)
- {
- If(a[i]<a[j])
- {
- Temp[index] = a[i];
- i = i+1;
- }
- Else
- {
- Temp[index] = a[j];
- j = j+1;
- }
- Index++;
- }
- If(i>mid)
- {
- While(j<=end)
- {
- Temp[index] = a[j];
- Index++;
- j++;
- }
- }
- Else
- {
- While(i<=mid)
- {
- Temp[index] = a[i];
- Index++;
- i++;
- }
- }
- k = beg;
- While(k<index)
- {
- a[k]=temp[k];
- k++;
- }
- }
Output:
Printing the sorted elements
7
9
10
12
23
23
34
44
78
101
Java Program
- Public class MyMergeSort
- {
- Void merge(int arr[], int beg, int mid, int end)
- {
- Int l = mid - beg + 1;
- Int r = end - mid;
- IntLeftArray[] = new int [l];
- IntRightArray[] = new int [r];
- For (int i=0; i<l; ++i)
- LeftArray[i] = arr[beg + i];
- For (int j=0; j<r; ++j)
- RightArray[j] = arr[mid + 1+ j];
- Int i = 0, j = 0;
- Int k = beg;
- While (i<l&&j<r)
- {
- If (LeftArray[i] <= RightArray[j])
- {
- Arr[k] = LeftArray[i];
- i++;
- }
- Else
- {
- Arr[k] = RightArray[j];
- j++;
- }
- k++;
- }
- While (i<l)
- {
- Arr[k] = LeftArray[i];
- i++;
- k++;
- }
- While (j<r)
- {
- Arr[k] = RightArray[j];
- j++;
- k++;
- }
- }
- Void sort(int arr[], int beg, int end)
- {
- If (beg<end)
- {
- Int mid = (beg+end)/2;
- Sort(arr, beg, mid);
- Sort(arr , mid+1, end);
- Merge(arr, beg, mid, end);
- }
- }
- Public static void main(String args[])
- {
- Intarr[] = {90,23,101,45,65,23,67,89,34,23};
- MyMergeSort ob = new MyMergeSort();
- Ob.sort(arr, 0, arr.length-1);
- System.out.println("\nSorted array");
- For(int i =0; i<arr.length;i++)
- {
- System.out.println(arr[i]+"");
- }
- }
- }
Output:
Sorted array
23
23
23
34
45
65
67
89
90
101
C# Program
- Using System;
- Public class MyMergeSort
- {
- Void merge(int[] arr, int beg, int mid, int end)
- {
- Int l = mid - beg + 1;
- Int r = end - mid;
- Int i,j;
- Int[] LeftArray = new int [l];
- Int[] RightArray = new int [r];
- For (i=0; i<l; ++i)
- LeftArray[i] = arr[beg + i];
- For (j=0; j<r; ++j)
- RightArray[j] = arr[mid + 1+ j];
- i = 0; j = 0;
- Int k = beg;
- While (i < l && j < r)
- {
- If (LeftArray[i] <= RightArray[j])
- {
- Arr[k] = LeftArray[i];
- i++;
- }
- Else
- {
- Arr[k] = RightArray[j];
- j++;
- }
- k++;
- }
- While (i < l)
- {
- Arr[k] = LeftArray[i];
- i++;
- k++;
- }
- While (j < r)
- {
- Arr[k] = RightArray[j];
- j++;
- k++;
- }
- }
- Void sort(int[] arr, int beg, int end)
- {
- If (beg < end)
- {
- Int mid = (beg+end)/2;
- Sort(arr, beg, mid);
- Sort(arr , mid+1, end);
- Merge(arr, beg, mid, end);
- }
- }
- Public static void Main()
- {
- Int[] arr = {90,23,101,45,65,23,67,89,34,23};
- MyMergeSort ob = new MyMergeSort();
- Ob.sort(arr, 0, 9);
- Console.WriteLine("\nSorted array");
- For(int i =0; i<10;i++)
- {
- Console.WriteLine(arr[i]+"");
- }
- }
- }
Output:
Sorted array
23
23
23
34
45
65
67
89
90
101
Shell Sort
Shell sort is the generalization of insertion sort which overcomes the drawbacks of insertion sort by comparing elements separated by a gap of several positions. In general, Shell sort performs the following steps.
- Step 1: Arrange the elements in the tabular form and sort the columns by using insertion sort.
- Step 2: Repeat Step 1; each time with smaller number of longer columns in such a way that at the end, there is only one column of data to be sorted.
Complexity
Complexity | Best Case | Average Case | Worst Case |
Time Complexity | Ω(n log(n)) | θ(n log(n)2) | O(n log(n)2) |
Space Complexity |
|
| O(1) |
Algorithm
Shell_Sort(Arr, n)
- Step 1: SET FLAG = 1, GAP_SIZE = N
- Step 2: Repeat Steps 3 to 6 while FLAG = 1 OR GAP_SIZE > 1
- Step 3:SET FLAG = 0
- Step 4:SET GAP_SIZE = (GAP_SIZE + 1) / 2
- Step 5:Repeat Step 6 for I = 0 to I < (N -GAP_SIZE)
- Step 6:IF Arr[I + GAP_SIZE] > Arr[I]
SWAP Arr[I + GAP_SIZE], Arr[I]
SET FLAG = 0 - Step 7: END
C Program
- #include <stdio.h>
- Void shellsort(int arr[], int num)
- {
- Int i, j, k, tmp;
- For (i = num / 2; i > 0; i = i / 2)
- {
- For (j = i; j < num; j++)
- {
- For(k = j - i; k >= 0; k = k - i)
- {
- If (arr[k+i] >= arr[k])
- Break;
- Else
- {
- Tmp = arr[k];
- Arr[k] = arr[k+i];
- Arr[k+i] = tmp;
- }
- }
- }
- }
- }
- Int main()
- {
- Int arr[30];
- Int k, num;
- Printf("Enter total no. of elements : ");
- Scanf("%d", &num);
- Printf("\nEnter %d numbers: ", num);
- For (k = 0 ; k < num; k++)
- {
- Scanf("%d", &arr[k]);
- }
- Shellsort(arr, num);
- Printf("\n Sorted array is: ");
- For (k = 0; k < num; k++)
- Printf("%d ", arr[k]);
- Return 0;
- }
Output:
Enter total no. Of elements : 6
Enter 6 numbers: 3
2
4
10
2
1
Sorted array is: 1 2 2 3 4 10
Java Program
- Import java.util.*;
- Public class Shell_Sort
- {
- Static void shellsort(int[] arr, intnum)
- {
- Int i, j, k, tmp;
- For (i = num / 2; i> 0; i = i / 2)
- {
- For (j = i; j<num; j++)
- {
- For(k = j - i; k>= 0; k = k - i)
- {
- If (arr[k+i] >= arr[k])
- Break;
- Else
- {
- Tmp = arr[k];
- Arr[k] = arr[k+i];
- Arr[k+i] = tmp;
- }
- }
- }
- }
- }
- Public static void main(String[] args)
- {
- Scanner sc = new Scanner(System.in);
- Int arr[]= newint[30];
- Intk, num;
- System.out.println("Enter total no. of elements : ");
- Num = sc.nextInt();
- For (k = 0 ; k<num; k++)
- {
- Arr[k]=sc.nextInt();
- }
- Shellsort(arr, num);
- System.out.println("\n Sorted array is: ");
- For (k = 0; k<num; k++)
- System.out.println(arr[k]);
- }
- }
Output:
Enter total no. Of elements : 6
3
2
4
10
2
1
Sorted array is: 1 2 2 3 4 10
C# Program
- Using System;
- Public class Shell_Sort
- {
- Static void shellsort(int[] arr, int num)
- {
- Int i, j, k, tmp;
- For (i = num / 2; i > 0; i = i / 2)
- {
- For (j = i; j < num; j++)
- {
- For(k = j - i; k >= 0; k = k - i)
- {
- If (arr[k+i] >= arr[k])
- Break;
- Else
- {
- Tmp = arr[k];
- Arr[k] = arr[k+i];
- Arr[k+i] = tmp;
- }
- }
- }
- }
- }
- Public void Main()
- {
- Int[] arr=new int[10];
- Int k, num;
- Console.WriteLine("Enter total no. of elements : ");
- Num = Convert.ToInt32(Console.ReadLine());
- For (k = 0 ; k < num; k++)
- {
- Arr[k]=Convert.ToInt32(Console.ReadLine());
- }
- Shellsort(arr, num);
- Console.WriteLine("\n Sorted array is: ");
- For (k = 0; k < num; k++)
- Console.WriteLine(arr[k]);
- }
- }
Output:
Enter total no. Of elements : 6
3
2
4
10
2
1
Sorted array is: 1 2 2 3 4 10
Comparison of sorting methods
Here we will see some sorting methods. There are 200+ sorting techniques. We will see few of them. Some sorting techniques are comparison based sort, some are non-comparison based sorting technique.
Comparison Based Soring techniques are bubble sort, selection sort, insertion sort, Merge sort, quicksort, heap sort etc. These techniques are considered as comparison based sort because in these techniques the values are compared, and placed into sorted position in ifferent phases. Here we will see time complexity of these techniques.
Analysis Type | Bubble Sort | Selection Sort | Insertion Sort | Merge Sort | Quick Sort | Heap Sort |
Best Case | O(n2) | O(n2) | O(n) | O(log n) | O(log n) | O(logn) |
Average Case | O(n2) | O(n2) | O(n2) | O(log n) | O(log n) | O(log n) |
Worst Case | O(n2) | O(n2) | O(n2) | O(log n) | O(n2) | O(log n) |
Some sorting algorithms are non-comparison based algorithm. Some of them are Radix sort, Bucket sort, count sort. These are non-comparison based sort because here two elements are not compared while sorting. The techniques are slightly different. Now we will see the difference between them based on different type of analysis.
Analysis Type | Radix Sort (k is maximum digit) | Counting Sort (k is size of count array) | Bucket Sort (k is number of buckets) |
Best Case | O(nk) | O(n + k) | O(n + k) |
Average Case | O(nk) | O(n + k) | O(n + k) |
Worst Case | O(nk) | O(n + k) | O(n2) |
Sorting techniques can also be compared using some other parameters. Some sorting algorithms are in-place sorting algorithms, and some are out-place sorting algorithms. Those algorithms, that does not require any extra space is called in-place sorting algorithm. Such as quicksort, heapsort algorithms are in-place. But merge sort is out-place sorting technique.
Some algorithms are online and some are offline. If the algorithm accepts new element while the sorting process is going on, that is called the online sorting algorithm. From the above mentioned techniques, the insertion sort is online sorting technique.
Analysis of different sorting techniques
In this article, we will discuss important properties of different sorting techniques including their complexity, stability and memory constraints. Before understanding this article, you should understand basics of different sorting techniques
Time complexity Analysis –
We have discussed the best, average and worst case complexity of different sorting techniques with possible scenarios.
Comparison based sorting –
In comparison based sorting, elements of an array are compared with each other to find the sorted array.
- Bubble sort and Insertion sort –
Average and worst case time complexity: n^2
Best case time complexity: n when array is already sorted.
Worst case: when the array is reverse sorted. - Selection sort –
Best, average and worst case time complexity: n^2 which is independent of distribution of data. - Merge sort –
Best, average and worst case time complexity: nlogn which is independent of distribution of data. - Heap sort –
Best, average and worst case time complexity: nlogn which is independent of distribution of data. - Quick sort –
It is a divide and conquer approach with recurrence relation: - T(n) = T(k) + T(n-k-1) + cn
Worst case: when the array is sorted or reverse sorted, the partition algorithm divides the array in two subarrays with 0 and n-1 elements. Therefore,
T(n) = T(0) + T(n-1) + cn
Solving this we get, T(n) = O(n^2)
Best case and Average case: On an average, the partition algorithm divides the array in two subarrays with equal size. Therefore,
T(n) = 2T(n/2) + cn
Solving this we get, T(n) = O(nlogn)
Non-comparison based sorting –
In non-comparison based sorting, elements of array are not compared with each other to find the sorted array.
- Radix sort –
Best, average and worst case time complexity: nk where k is the maximum number of digits in elements of array. - Count sort –
Best, average and worst case time complexity: n+k where k is the size of count array. - Bucket sort –
Best and average time complexity: n+k where k is the number of buckets.
Worst case time complexity: n^2 if all elements belong to same bucket.
In-place/Outplace technique –
A sorting technique is inplace if it does not use any extra memory to sort the array.
Among the comparison based techniques discussed, only merge sort is outplaced technique as it requires an extra array to merge the sorted subarrays.
Among the non-comparison based techniques discussed, all are outplaced techniques. Counting sort uses a counting array and bucket sort uses a hash table for sorting the array.
Online/Offline technique –
A sorting technique is considered Online if it can accept new data while the procedure is ongoing i.e. complete data is not required to start the sorting operation.
Among the comparison based techniques discussed, only Insertion Sort qualifies for this because of the underlying algorithm it uses i.e. it processes the array (not just elements) from left to right and if new elements are added to the right, it doesn’t impact the ongoing operation.
Stable/Unstable technique –
A sorting technique is stable if it does not change the order of elements with the same value.
Out of comparison based techniques, bubble sort, insertion sort and merge sort are stable techniques. Selection sort is unstable as it may change the order of elements with the same value. For example, consider the array 4, 4, 1, 3.
In the first iteration, the minimum element found is 1 and it is swapped with 4 at 0th position. Therefore, the order of 4 with respect to 4 at the 1st position will change. Similarly, quick sort and heap sort are also unstable.
Out of non-comparison based techniques, Counting sort and Bucket sort are stable sorting techniques whereas radix sort stability depends on the underlying algorithm used for sorting.
Analysis of sorting techniques :
- When the array is almost sorted, insertion sort can be preferred.
- When order of input is not known, merge sort is preferred as it has worst case time complexity of nlogn and it is stable as well.
- When the array is sorted, insertion and bubble sort gives complexity of n but quick sort gives complexity of n^2.
Time and Space Complexity Comparison Table :
Sorting Algorithm | Time Complexity | Space Complexity | ||
| Best Case | Average Case | Worst Case | Worst Case |
Bubble Sort | Ω(N) | Θ(N2) | O(N2) | O(1) |
Selection Sort | Ω(N2) | Θ(N2) | O(N2) | O(1) |
Insertion Sort | Ω(N) | Θ(N2) | O(N2) | O(1) |
Merge Sort | Ω(N log N) | Θ(N log N) | O(N log N) | O(N) |
Heap Sort | Ω(N log N) | Θ(N log N) | O(N log N) | O(1) |
Quick Sort | Ω(N log N) | Θ(N log N) | O(N2) | O(N log N) |
Radix Sort | Ω(N k) | Θ(N k) | O(N k) | O(N + k) |
Count Sort | Ω(N + k) | Θ(N + k) | O(N + k) | O(k) |
Bucket Sort | Ω(N + k) | Θ(N + k) | O(N2) | O(N) |
Asymptotic analysis overcomes the problems of naive way of analyzing algorithms. In this post, we will take an example of Linear Search and analyze it using Asymptotic analysis.
We can have three cases to analyze an algorithm:
1) The Worst Case
2) Average Case
3) Best Case
Let us consider the following implementation of Linear Search.
// C++ implementation of the approach #include <bits/stdc++.h> Using namespace std;
// Linearly search x in arr[]. // If x is present then return the index, // otherwise return -1 Int search(int arr[], int n, int x) { Int i; For (i = 0; i < n; i++) { If (arr[i] == x) Return i; } Return -1; }
// Driver Code Int main() { Int arr[] = { 1, 10, 30, 15 }; Int x = 30; Int n = sizeof(arr) / sizeof(arr[0]); Cout << x << " is present at index " << search(arr, n, x);
Getchar(); Return 0; }
// This code is contributed // by Akanksha Rai |
Output:
30 is present at index 2
Worst Case Analysis (Usually Done)
In the worst case analysis, we calculate upper bound on running time of an algorithm. We must know the case that causes maximum number of operations to be executed. For Linear Search, the worst case happens when the element to be searched (x in the above code) is not present in the array. When x is not present, the search() functions compares it with all the elements of arr[] one by one. Therefore, the worst case time complexity of linear search would be Θ(n).
Average Case Analysis (Sometimes done)
In average case analysis, we take all possible inputs and calculate computing time for all of the inputs. Sum all the calculated values and divide the sum by total number of inputs. We must know (or predict) distribution of cases. For the linear search problem, let us assume that all cases are (including the case of x not being present in array). So we sum all the cases and divide the sum by (n+1). Following is the value of average case time complexity.
Average Case Time =
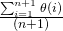 =
= 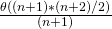
= Θ(n)
Best Case Analysis (Bogus)
In the best case analysis, we calculate lower bound on running time of an algorithm. We must know the case that causes minimum number of operations to be executed. In the linear search problem, the best case occurs when x is present at the first location. The number of operations in the best case is constant (not dependent on n). So time complexity in the best case would be Θ(1)
Most of the times, we do worst case analysis to analyze algorithms. In the worst analysis, we guarantee an upper bound on the running time of an algorithm which is good information.
The average case analysis is not easy to do in most of the practical cases and it is rarely done. In the average case analysis, we must know (or predict) the mathematical distribution of all possible inputs.
The Best Case analysis is bogus. Guaranteeing a lower bound on an algorithm doesn’t provide any information as in the worst case, an algorithm may take years to run.
For some algorithms, all the cases are asymptotically same, i.e., there are no worst and best cases. For example,merge sort. Merge Sort does Θ(nLogn) operations in all cases. Most of the other sorting algorithms have worst and best cases. For example, in the typical implementation of Quick Sort (where pivot is chosen as a corner element), the worst occurs when the input array is already sorted and the best occur when the pivot elements always divide array in two halves. For insertion sort, the worst case occurs when the array is reverse sorted and the best case occurs when the array is sorted in the same order as output.
References:
1. G. A.V, PAI , “Data Structures and Algorithms “, McGraw Hill, ISBN -13: 978-0-07-066726-6
2. A. Tharp ,"File Organization and Processing", 2008 ,Willey India edition, 9788126518685
3. M. Folk, B. Zoellick, G. Riccardi, "File Structure An Object Oriented Approach with C++", Pearson Education, 2002, ISBN 81 - 7808 - 131 - 8.
4. M. Welss, “Data Structures and Algorithm Analysis in C++", 2nd edition, Pearson Education, 2002, ISBN81-7808-670-0