Unit 3
Stack & Queue
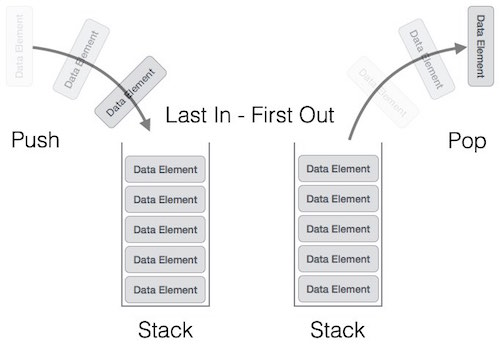
A stack is an Abstract Data Type (ADT), commonly used in most programming languages. It is named stack as it behaves like a real-world stack, for example – a deck of cards or a pile of plates, etc.
A real-world stack allows operations at one end only. For example, we can place or remove a card or plate from the top of the stack only. Likewise, Stack ADT allows all data operations at one end only. At any given time, we can only access the top element of a stack.
This feature makes it LIFO data structure. LIFO stands for Last-in-first-out. Here, the element which is placed (inserted or added) last, is accessed first. In stack terminology, insertion operation is called PUSH operation and removal operation is called POP operation.
Stack Representation
The following diagram depicts a stack and its operations −
A stack can be implemented by means of Array, Structure, Pointer, and Linked List. Stack can either be a fixed size one or it may have a sense of dynamic resizing. Here, we are going to implement stack using arrays, which makes it a fixed size stack implementation.
Basic Operations
Stack operations may involve initializing the stack, using it and then de-initializing it. Apart from these basic stuffs, a stack is used for the following two primary operations −
- Push() − Pushing (storing) an element on the stack.
- Pop() − Removing (accessing) an element from the stack.
When data is PUSHed onto stack.
To use a stack efficiently, we need to check the status of stack as well. For the same purpose, the following functionality is added to stacks −
- Peek() − get the top data element of the stack, without removing it.
- IsFull() − check if stack is full.
- IsEmpty() − check if stack is empty.
At all times, we maintain a pointer to the last PUSHed data on the stack. As this pointer always represents the top of the stack, hence named top. The top pointer provides top value of the stack without actually removing it.
First we should learn about procedures to support stack functions −
Peek()
Algorithm of peek() function −
Begin procedure peek
Return stack[top]
End procedure
Implementation of peek() function in C programming language −
Example
Int peek() {
Return stack[top];
}
Isfull()
Algorithm of isfull() function −
Begin procedure isfull
If top equals to MAXSIZE
Return true
Else
Return false
Endif
End procedure
Implementation of isfull() function in C programming language −
Example
Bool isfull() {
If(top == MAXSIZE)
Return true;
Else
Return false;
}
Isempty()
Algorithm of isempty() function −
Begin procedure isempty
If top less than 1
Return true
Else
Return false
Endif
End procedure
Implementation of isempty() function in C programming language is slightly different. We initialize top at -1, as the index in array starts from 0. So we check if the top is below zero or -1 to determine if the stack is empty. Here's the code −
Example
Bool isempty() {
If(top == -1)
Return true;
Else
Return false;
}
Push Operation
The process of putting a new data element onto stack is known as a Push Operation. Push operation involves a series of steps −
- Step 1 − Checks if the stack is full.
- Step 2 − If the stack is full, produces an error and exit.
- Step 3 − If the stack is not full, increments top to point next empty space.
- Step 4 − Adds data element to the stack location, where top is pointing.
- Step 5 − Returns success.
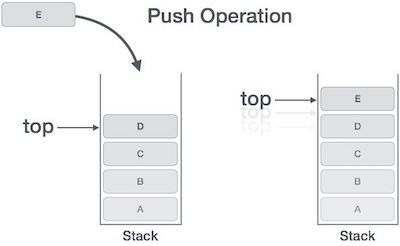
If the linked list is used to implement the stack, then in step 3, we need to allocate space dynamically.
Algorithm for PUSH Operation
A simple algorithm for Push operation can be derived as follows −
Begin procedure push: stack, data
If stack is full
Return null
Endif
Top ← top + 1
Stack[top] ← data
End procedure
Implementation of this algorithm in C, is very easy. See the following code −
Example
Void push(int data) {
If(!isFull()) {
Top = top + 1;
Stack[top] = data;
} else {
Printf("Could not insert data, Stack is full.\n");
}
}
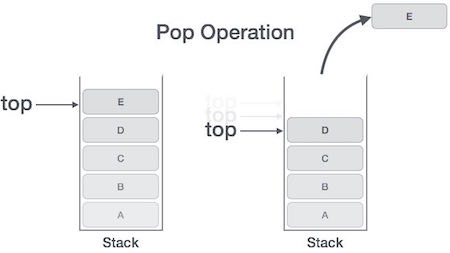
Pop Operation
Accessing the content while removing it from the stack, is known as a Pop Operation. In an array implementation of pop() operation, the data element is not actually removed, instead top is decremented to a lower position in the stack to point to the next value. But in linked-list implementation, pop() actually removes data element and deallocates memory space.
A Pop operation may involve the following steps −
- Step 1 − Checks if the stack is empty.
- Step 2 − If the stack is empty, produces an error and exit.
- Step 3 − If the stack is not empty, accesses the data element at which top is pointing.
- Step 4 − Decreases the value of top by 1.
- Step 5 − Returns success.
Algorithm for Pop Operation
A simple algorithm for Pop operation can be derived as follows −
Begin procedure pop: stack
If stack is empty
Return null
Endif
Data ← stack[top]
Top ← top - 1
Return data
End procedure
Implementation of this algorithm in C, is as follows −
Example
Int pop(int data) {
If(!isempty()) {
Data = stack[top];
Top = top - 1;
Return data;
} else {
Printf("Could not retrieve data, Stack is empty.\n");
}
}
Databases such as ORACLE have a memory area, where processing of instructions and fetched data takes place.A cursor is a pointer which is pointing to this area.The data contained in this memory area is also known as Active Set. Cursors can be broadly classified into Implict Cursors and Explicit Cursors.
Implicit | Explicit |
Implicit cursors are automatically created when select statements are executed. | Explicit cursors needs to be defined explicitly by the user by providing a name. |
They are capable of fetching a single row at a time. | Explicit cursors can fetch multiple rows. |
They are more vulnerable to errors such as Data errors, etc. | They are less vulnerable to errors(Data errors etc.) |
Provides less programmatic control to the users | User/Programmer has the entire control. |
Implicit cursors are less efficient. | Comparitive to Implicit cursors, explicit cursors are more efficient. |
Implicit Cursors are defined as: BEGIN SELECT attr_name from table_name Where CONDITION; END | Explicit cursors are defined as: DECLARE CURSOR cur_name IS SELECT attr_name from table_name Where CONDITION; BEGIN ... |
Implicit cursors requires anonymous buffer memory for storage purpose. | Explicit cursors use user-defined memory space for storage purpose |
Cursor attributes use prefix “SQL”. | Structure for explicit cursors: cur_name%attr_name |
Instead of using array, we can also use linked list to implement stack. Linked list allocates the memory dynamically. However, time complexity in both the scenario is same for all the operations i.e. push, pop and peek.
In linked list implementation of stack, the nodes are maintained non-contiguously in the memory. Each node contains a pointer to its immediate successor node in the stack. Stack is said to be overflown if the space left in the memory heap is not enough to create a node.
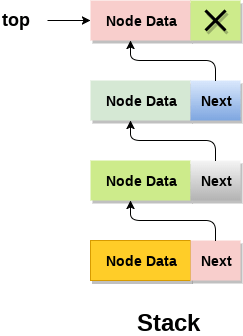
The top most node in the stack always contains null in its address field. Lets discuss the way in which, each operation is performed in linked list implementation of stack.
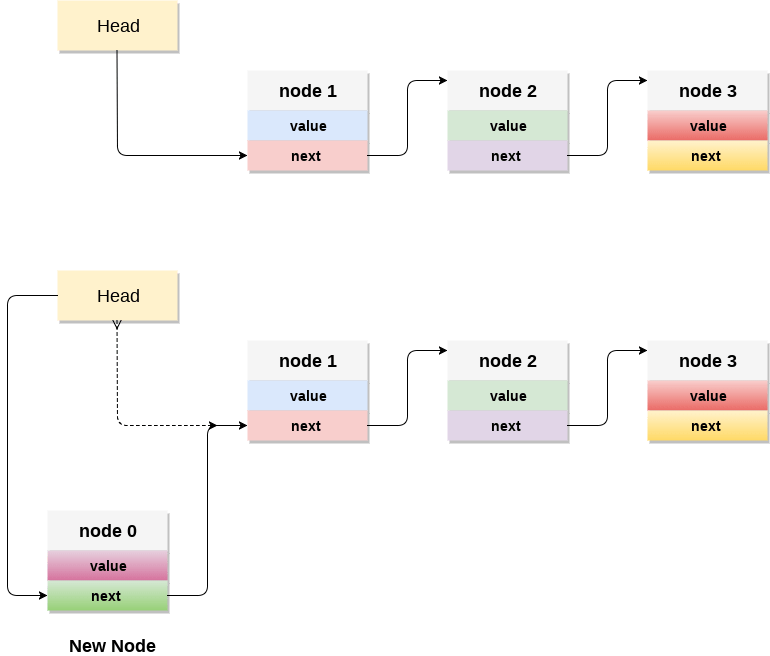
Adding a node to the stack (Push operation)
Adding a node to the stack is referred to as push operation. Pushing an element to a stack in linked list implementation is different from that of an array implementation. In order to push an element onto the stack, the following steps are involved.
- Create a node first and allocate memory to it.
- If the list is empty then the item is to be pushed as the start node of the list. This includes assigning value to the data part of the node and assign null to the address part of the node.
- If there are some nodes in the list already, then we have to add the new element in the beginning of the list (to not violate the property of the stack). For this purpose, assign the address of the starting element to the address field of the new node and make the new node, the starting node of the list.
Time Complexity : o(1)
C implementation :
- Void push ()
- {
- Int val;
- Struct node *ptr =(struct node*)malloc(sizeof(struct node));
- If(ptr == NULL)
- {
- Printf("not able to push the element");
- }
- Else
- {
- Printf("Enter the value");
- Scanf("%d",&val);
- If(head==NULL)
- {
- Ptr->val = val;
- Ptr -> next = NULL;
- Head=ptr;
- }
- Else
- {
- Ptr->val = val;
- Ptr->next = head;
- Head=ptr;
- }
- Printf("Item pushed");
- }
- }
Deleting a node from the stack (POP operation)
Deleting a node from the top of stack is referred to as pop operation. Deleting a node from the linked list implementation of stack is different from that in the array implementation. In order to pop an element from the stack, we need to follow the following steps :
30. Check for the underflow condition: The underflow condition occurs when we try to pop from an already empty stack. The stack will be empty if the head pointer of the list points to null.
31. Adjust the head pointer accordingly: In stack, the elements are popped only from one end, therefore, the value stored in the head pointer must be deleted and the node must be freed. The next node of the head node now becomes the head node.
Time Complexity : o(n)
C implementation
32. void pop()
33. {
34. int item;
35. struct node *ptr;
36. if (head == NULL)
37. {
38. printf("Underflow");
39. }
40. else
41. {
42. item = head->val;
43. ptr = head;
44. head = head->next;
45. free(ptr);
46. printf("Item popped");
47.
48. }
49. }
Display the nodes (Traversing)
Displaying all the nodes of a stack needs traversing all the nodes of the linked list organized in the form of stack. For this purpose, we need to follow the following steps.
50. Copy the head pointer into a temporary pointer.
51. Move the temporary pointer through all the nodes of the list and print the value field attached to every node.
Time Complexity : o(n)
C Implementation
52. void display()
53. {
54. int i;
55. struct node *ptr;
56. ptr=head;
57. if(ptr == NULL)
58. {
59. printf("Stack is empty\n");
60. }
61. else
62. {
63. printf("Printing Stack elements \n");
64. while(ptr!=NULL)
65. {
66. printf("%d\n",ptr->val);
67. ptr = ptr->next;
68. }
69. }
70. }
Menu Driven program in C implementing all the stack operations using linked list:
71. #include <stdio.h>
72. #include <stdlib.h>
73. void push();
74. void pop();
75. void display();
76. struct node
77. {
78. int val;
79. struct node *next;
80. };
81. struct node *head;
82.
83. void main ()
84. {
85. int choice=0;
86. printf("\n*********Stack operations using linked list*********\n");
87. printf("\n----------------------------------------------\n");
88. while(choice != 4)
89. {
90. printf("\n\nChose one from the below options...\n");
91. printf("\n1.Push\n2.Pop\n3.Show\n4.Exit");
92. printf("\n Enter your choice \n");
93. scanf("%d",&choice);
94. switch(choice)
95. {
96. case 1:
97. {
98. push();
99. break;
100. }
101. case 2:
102. {
103. pop();
104. break;
105. }
106. case 3:
107. {
108. display();
109. break;
110. }
111. case 4:
112. {
113. printf("Exiting....");
114. break;
115. }
116. default:
117. {
118. printf("Please Enter valid choice ");
119. }
120. };
121. }
122. }
123. void push ()
124. {
125. int val;
126. struct node *ptr = (struct node*)malloc(sizeof(struct node));
127. if(ptr == NULL)
128. {
129. printf("not able to push the element");
130. }
131. else
132. {
133. printf("Enter the value");
134. scanf("%d",&val);
135. if(head==NULL)
136. {
137. ptr->val = val;
138. ptr -> next = NULL;
139. head=ptr;
140. }
141. else
142. {
143. ptr->val = val;
144. ptr->next = head;
145. head=ptr;
146.
147. }
148. printf("Item pushed");
149.
150. }
151. }
152.
153. void pop()
154. {
155. int item;
156. struct node *ptr;
157. if (head == NULL)
158. {
159. printf("Underflow");
160. }
161. else
162. {
163. item = head->val;
164. ptr = head;
165. head = head->next;
166. free(ptr);
167. printf("Item popped");
168.
169. }
170. }
171. void display()
172. {
173. int i;
174. struct node *ptr;
175. ptr=head;
176. if(ptr == NULL)
177. {
178. printf("Stack is empty\n");
179. }
180. else
181. {
182. printf("Printing Stack elements \n");
183. while(ptr!=NULL)
184. {
185. printf("%d\n",ptr->val);
186. ptr = ptr->next;
187. }
188. }
189. }
Recursion is the process which comes into existence when a function calls a copy of itself to work on a smaller problem. Any function which calls itself is called recursive function, and such function calls are called recursive calls. Recursion involves several numbers of recursive calls. However, it is important to impose a termination condition of recursion. Recursion code is shorter than iterative code however it is difficult to understand.
Recursion cannot be applied to all the problem, but it is more useful for the tasks that can be defined in terms of similar subtasks. For Example, recursion may be applied to sorting, searching, and traversal problems.
Generally, iterative solutions are more efficient than recursion since function call is always overhead. Any problem that can be solved recursively, can also be solved iteratively. However, some problems are best suited to be solved by the recursion, for example, tower of Hanoi, Fibonacci series, factorial finding, etc.
In the following example, recursion is used to calculate the factorial of a number.
- #include <stdio.h>
- Int fact (int);
- Int main()
- {
- Int n,f;
- Printf("Enter the number whose factorial you want to calculate?");
- Scanf("%d",&n);
- f = fact(n);
- Printf("factorial = %d",f);
- }
- Int fact(int n)
- {
- If (n==0)
- {
- Return 0;
- }
- Else if ( n == 1)
- {
- Return 1;
- }
- Else
- {
- Return n*fact(n-1);
- }
- }
Output
Enter the number whose factorial you want to calculate?5
Factorial = 120
We can understand the above program of the recursive method call by the figure given below:
Recursive Function
A recursive function performs the tasks by dividing it into the subtasks. There is a termination condition defined in the function which is satisfied by some specific subtask. After this, the recursion stops and the final result is returned from the function.
The case at which the function doesn't recur is called the base case whereas the instances where the function keeps calling itself to perform a subtask, is called the recursive case. All the recursive functions can be written using this format.
Pseudocode for writing any recursive function is given below.
- If (test_for_base)
- {
- Return some_value;
- }
- Else if (test_for_another_base)
- {
- Return some_another_value;
- }
- Else
- {
- // Statements;
- Recursive call;
- }
Example of recursion
Let's see an example to find the nth term of the Fibonacci series.
- #include<stdio.h>
- Int fibonacci(int);
- Void main ()
- {
- Int n,f;
- Printf("Enter the value of n?");
- Scanf("%d",&n);
- f = fibonacci(n);
- Printf("%d",f);
- }
- Int fibonacci (int n)
- {
- If (n==0)
- {
- Return 0;
- }
- Else if (n == 1)
- {
- Return 1;
- }
- Else
- {
- Return fibonacci(n-1)+fibonacci(n-2);
- }
- }
Output
Enter the value of n?12
144
Memory allocation of Recursive method
Each recursive call creates a new copy of that method in the memory. Once some data is returned by the method, the copy is removed from the memory. Since all the variables and other stuff declared inside function get stored in the stack, therefore a separate stack is maintained at each recursive call. Once the value is returned from the corresponding function, the stack gets destroyed. Recursion involves so much complexity in resolving and tracking the values at each recursive call. Therefore we need to maintain the stack and track the values of the variables defined in the stack.
Let us consider the following example to understand the memory allocation of the recursive functions.
- Int display (int n)
- {
- If(n == 0)
- Return 0; // terminating condition
- Else
- {
- Printf("%d",n);
- Return display(n-1); // recursive call
- }
- }
Explanation
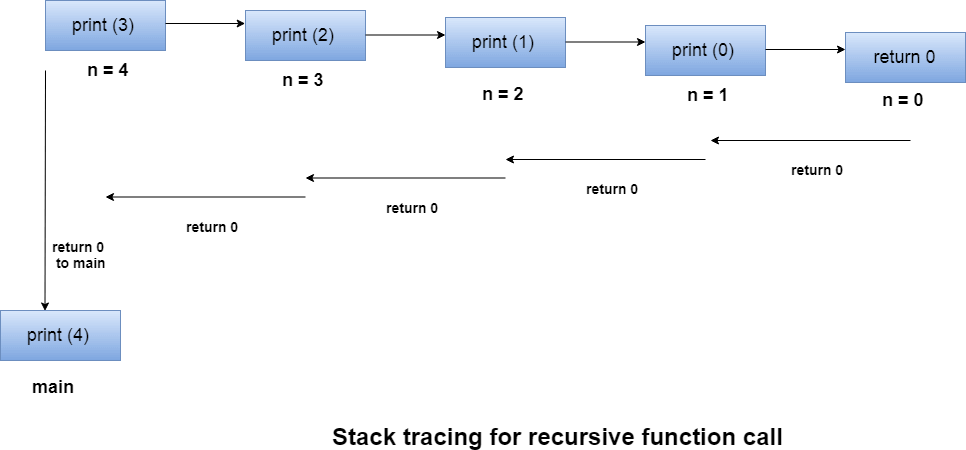
Let us examine this recursive function for n = 4. First, all the stacks are maintained which prints the corresponding value of n until n becomes 0, Once the termination condition is reached, the stacks get destroyed one by one by returning 0 to its calling stack. Consider the following image for more information regarding the stack trace for the recursive functions.
Infix expressions are readable and solvable by humans. We can easily distinguish the order of operators, and also can use the parenthesis to solve that part first during solving mathematical expressions. The computer cannot differentiate the operators and parenthesis easily, that’s why postfix conversion is needed.
To convert infix expression to postfix expression, we will use the stack data structure. By scanning the infix expression from left to right, when we will get any operand, simply add them to the postfix form, and for the operator and parenthesis, add them in the stack maintaining the precedence of them.
Note: Here we will consider only {+, −,∗,/, ^} operators, other operators are neglected.
Input and Output
Input:
The infix expression. x^y/(5*z)+2
Output:
Postfix Form Is: xy^5z*/2+
Algorithm
InfixToPostfix(infix)
Input − Infix expression.
Output − Convert infix expression to postfix form.
Begin
Initially push some special character say # into the stack
For each character ch from infix expression, do
If ch is alphanumeric character, then
Add ch to postfix expression
Else if ch = opening parenthesis (, then
Push ( into stack
Else if ch = ^, then //exponential operator of higher precedence
Push ^ into the stack
Else if ch = closing parenthesis ), then
While stack is not empty and stack top ≠ (,
Do pop and add item from stack to postfix expression
Done
Pop ( also from the stack
Else
While stack is not empty AND precedence of ch <= precedence of stack top element, do
Pop and add into postfix expression
Done
Push the newly coming character.
Done
While the stack contains some remaining characters, do
Pop and add to the postfix expression
Done
Return postfix
End
Example
#include<iostream>
#include<stack>
#include<locale> //for function isalnum()
Using namespace std;
Int preced(char ch) {
If(ch == '+' || ch == '-') {
Return 1; //Precedence of + or - is 1
}else if(ch == '*' || ch == '/') {
Return 2; //Precedence of * or / is 2
}else if(ch == '^') {
Return 3; //Precedence of ^ is 3
}else {
Return 0;
}
}
String inToPost(string infix ) {
Stack<char> stk;
Stk.push('#'); //add some extra character to avoid underflow
String postfix = ""; //initially the postfix string is empty
String::iterator it;
For(it = infix.begin(); it!=infix.end(); it++) {
If(isalnum(char(*it)))
Postfix += *it; //add to postfix when character is letter or number
Else if(*it == '(')
Stk.push('(');
Else if(*it == '^')
Stk.push('^');
Else if(*it == ')') {
While(stk.top() != '#' && stk.top() != '(') {
Postfix += stk.top(); //store and pop until ( has found
Stk.pop();
}
Stk.pop(); //remove the '(' from stack
}else {
If(preced(*it) > preced(stk.top()))
Stk.push(*it); //push if precedence is high
Else {
While(stk.top() != '#' && preced(*it) <= preced(stk.top())) {
Postfix += stk.top(); //store and pop until higher precedence is found
Stk.pop();
}
Stk.push(*it);
}
}
}
While(stk.top() != '#') {
Postfix += stk.top(); //store and pop until stack is not empty.
Stk.pop();
}
Return postfix;
}
Int main() {
String infix = "x^y/(5*z)+2";
Cout << "Postfix Form Is: " << inToPost(infix) << endl;
}
Output
Postfix Form Is: xy^5z*/2+
Postfix Expression
For solving a mathematical expression, we need prefix or postfix form. After converting infix to postfix, we need postfix evaluation algorithm to find the correct answer.
Here also we have to use the stack data structure to solve the postfix expressions.
From the postfix expression, when some operands are found, pushed them in the stack. When some operator is found, two items are popped from the stack and the operation is performed in correct sequence. After that, the result is also pushed in the stack for future use. After completing the whole expression, the final result is also stored in the stack top.
Input and Output
Input:
Postfix expression: 53+62/*35*+
Output:
The result is: 39
Algorithm
PostfixEvaluation(postfix)
Input: Postfix expression to evaluate.
Output: Answer after evaluating postfix form.
Begin
For each character ch in the postfix expression, do
If ch is an operator ⨀ , then
a := pop first element from stack
b := pop second element from the stack
Res := b ⨀ a
Push res into the stack
Else if ch is an operand, then
Add ch into the stack
Done
Return element of stack top
End
Example
#include<iostream>
#include<cmath>
#include<stack>
Using namespace std;
Float scanNum(char ch) {
Int value;
Value = ch;
Return float(value-'0'); //return float from character
}
Int isOperator(char ch) {
If(ch == '+'|| ch == '-'|| ch == '*'|| ch == '/' || ch == '^')
Return 1; //character is an operator
Return -1; //not an operator
}
Int isOperand(char ch) {
If(ch >= '0' && ch <= '9')
Return 1; //character is an operand
Return -1; //not an operand
}
Float operation(int a, int b, char op) {
//Perform operation
If(op == '+')
Return b+a;
Else if(op == '-')
Return b-a;
Else if(op == '*')
Return b*a;
Else if(op == '/')
Return b/a;
Else if(op == '^')
Return pow(b,a); //find b^a
Else
Return INT_MIN; //return negative infinity
}
Float postfixEval(string postfix) {
Int a, b;
Stack<float> stk;
String::iterator it;
For(it=postfix.begin(); it!=postfix.end(); it++) {
//read elements and perform postfix evaluation
If(isOperator(*it) != -1) {
a = stk.top();
Stk.pop();
b = stk.top();
Stk.pop();
Stk.push(operation(a, b, *it));
}else if(isOperand(*it) > 0) {
Stk.push(scanNum(*it));
}
}
Return stk.top();
}
Main() {
String post = "53+62/*35*+";
Cout << "The result is: "<<postfixEval(post);
}
Output
The result is: 39
Prefix Expressions
Prefix and Postfix expressions can be evaluated faster than an infix expression. This is because we don’t need to process any brackets or follow operator precedence rule. In postfix and prefix expressions which ever operator comes before will be evaluated first, irrespective of its priority. Also, there are no brackets in these expressions. As long as we can guarantee that a valid prefix or postfix expression is used, it can be evaluated with correctness.
In this article, we will discuss how to evaluate an expression written in prefix notation. The method is similar to evaluating a postfix expression.
Algorithm
EVALUATE_PREFIX(STRING)
Step 1: Put a pointer P at the end of the end
Step 2: If character at P is an operand push it to Stack
Step 3: If the character at P is an operator pop two
Elements from the Stack. Operate on these elements
According to the operator, and push the result
Back to the Stack
Step 4: Decrement P by 1 and go to Step 2 as long as there
Are characters left to be scanned in the expression.
Step 5: The Result is stored at the top of the Stack,
Return it
Step 6: End
Example to demonstrate working of the algorithm
Expression: +9*26
Character | Stack | Explanation
Scanned | (Front to |
| Back) |
-------------------------------------------
6 6 6 is an operand,
Push to Stack
2 6 2 2 is an operand,
Push to Stack
* 12 (6*2) * is an operator,
Pop 6 and 2, multiply
Them and push result
To Stack
9 12 9 9 is an operand, push
To Stack
+ 21 (12+9) + is an operator, pop
12 and 9 add them and
Push result to Stack
Result: 21
Examples:
Input : -+8/632
Output : 8
Input : -+7*45+20
Output : 25
Complexity The algorithm has linear complexity since we scan the expression once and perform at most O(N) push and pop operations which take constant time.
Implementation of the algorithm is given below.
// C++ program to evaluate a prefix expression. #include <bits/stdc++.h> Using namespace std;
Bool isOperand(char c) { // If the character is a digit then it must // be an operand Return isdigit(c); }
Double evaluatePrefix(string exprsn) { Stack<double> Stack;
For (int j = exprsn.size() - 1; j >= 0; j--) {
// Push operand to Stack // To convert exprsn[j] to digit subtract // '0' from exprsn[j]. If (isOperand(exprsn[j])) Stack.push(exprsn[j] - '0');
Else {
// Operator encountered // Pop two elements from Stack Double o1 = Stack.top(); Stack.pop(); Double o2 = Stack.top(); Stack.pop();
// Use switch case to operate on o1 // and o2 and perform o1 O o2. Switch (exprsn[j]) { Case '+': Stack.push(o1 + o2); Break; Case '-': Stack.push(o1 - o2); Break; Case '*': Stack.push(o1 * o2); Break; Case '/': Stack.push(o1 / o2); Break; } } }
Return Stack.top(); }
// Driver code Int main() { String exprsn = "+9*26"; Cout << evaluatePrefix(exprsn) << endl; Return 0; } |
Output:
21
Note:
To perform more types of operations only the switch case table needs to be modified. This implementation works only for single digit operands. Multi-digit operands can be implemented if some character like space is used to separate the operands and operators.
Queue is an abstract data structure, somewhat similar to Stacks. Unlike stacks, a queue is open at both its ends. One end is always used to insert data (enqueue) and the other is used to remove data (dequeue). Queue follows First-In-First-Out methodology, i.e., the data item stored first will be accessed first.
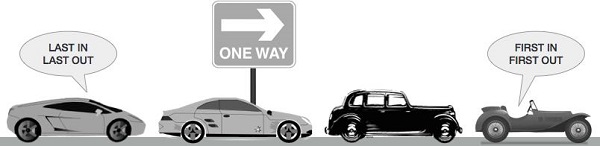
A real-world example of queue can be a single-lane one-way road, where the vehicle enters first, exits first. More real-world examples can be seen as queues at the ticket windows and bus-stops.
Queue Representation
As we now understand that in queue, we access both ends for different reasons. The following diagram given below tries to explain queue representation as data structure −
As in stacks, a queue can also be implemented using Arrays, Linked-lists, Pointers and Structures. For the sake of simplicity, we shall implement queues using one-dimensional array.
Basic Operations
Queue operations may involve initializing or defining the queue, utilizing it, and then completely erasing it from the memory. Here we shall try to understand the basic operations associated with queues −
- Enqueue() − add (store) an item to the queue.
- Dequeue() − remove (access) an item from the queue.
Few more functions are required to make the above-mentioned queue operation efficient. These are −
- Peek() − Gets the element at the front of the queue without removing it.
- Isfull() − Checks if the queue is full.
- Isempty() − Checks if the queue is empty.
In queue, we always dequeue (or access) data, pointed by front pointer and while enqueing (or storing) data in the queue we take help of rear pointer.
Let's first learn about supportive functions of a queue −
Peek()
This function helps to see the data at the front of the queue. The algorithm of peek() function is as follows −
Algorithm
Begin procedure peek
Return queue[front]
End procedure
Implementation of peek() function in C programming language −
Example
Int peek() {
Return queue[front];
}
Isfull()
As we are using single dimension array to implement queue, we just check for the rear pointer to reach at MAXSIZE to determine that the queue is full. In case we maintain the queue in a circular linked-list, the algorithm will differ. Algorithm of isfull() function −
Algorithm
Begin procedure isfull
If rear equals to MAXSIZE
Return true
Else
Return false
Endif
End procedure
Implementation of isfull() function in C programming language −
Example
Bool isfull() {
If(rear == MAXSIZE - 1)
Return true;
Else
Return false;
}
Isempty()
Algorithm of isempty() function −
Algorithm
Begin procedure isempty
If front is less than MIN OR front is greater than rear
Return true
Else
Return false
Endif
End procedure
If the value of front is less than MIN or 0, it tells that the queue is not yet initialized, hence empty.
Here's the C programming code −
Example
Bool isempty() {
If(front < 0 || front > rear)
Return true;
Else
Return false;
}
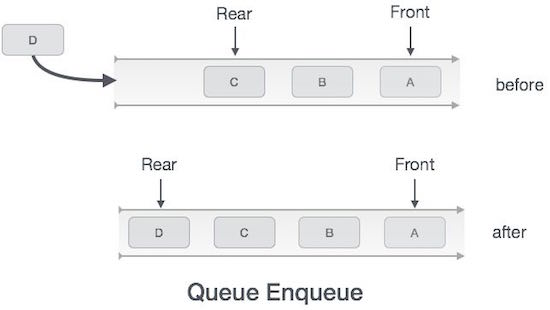
Enqueue Operation
Queues maintain two data pointers, front and rear. Therefore, its operations are comparatively difficult to implement than that of stacks.
The following steps should be taken to enqueue (insert) data into a queue −
- Step 1 − Check if the queue is full.
- Step 2 − If the queue is full, produce overflow error and exit.
- Step 3 − If the queue is not full, increment rear pointer to point the next empty space.
- Step 4 − Add data element to the queue location, where the rear is pointing.
- Step 5 − return success.
Sometimes, we also check to see if a queue is initialized or not, to handle any unforeseen situations.
Algorithm for enqueue operation
Procedure enqueue(data)
If queue is full
Return overflow
Endif
Rear ← rear + 1
Queue[rear] ← data
Return true
End procedure
Implementation of enqueue() in C programming language −
Example
Int enqueue(int data)
If(isfull())
Return 0;
Rear = rear + 1;
Queue[rear] = data;
Return 1;
End procedure
Dequeue Operation
Accessing data from the queue is a process of two tasks − access the data where front is pointing and remove the data after access. The following steps are taken to perform dequeue operation −
- Step 1 − Check if the queue is empty.
- Step 2 − If the queue is empty, produce underflow error and exit.
- Step 3 − If the queue is not empty, access the data where front is pointing.
- Step 4 − Increment front pointer to point to the next available data element.
- Step 5 − Return success.
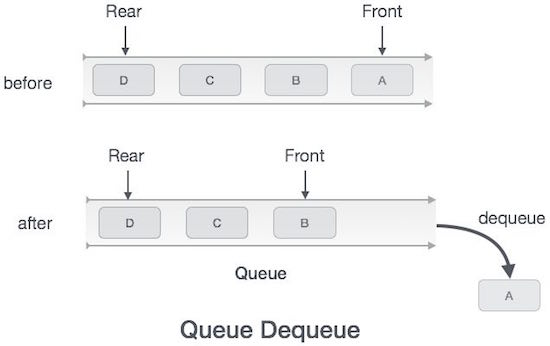
Algorithm for dequeue operation
Procedure dequeue
If queue is empty
Return underflow
End if
Data = queue[front]
Front ← front + 1
Return true
End procedure
Implementation of dequeue() in C programming language −
Example
Int dequeue() {
If(isempty())
Return 0;
Int data = queue[front];
Front = front + 1;
Return data;
}
The array implementation can not be used for the large scale applications where the queues are implemented. One of the alternative of array implementation is linked list implementation of queue.
The storage requirement of linked representation of a queue with n elements is o(n) while the time requirement for operations is o(1).
In a linked queue, each node of the queue consists of two parts i.e. data part and the link part. Each element of the queue points to its immediate next element in the memory.
In the linked queue, there are two pointers maintained in the memory i.e. front pointer and rear pointer. The front pointer contains the address of the starting element of the queue while the rear pointer contains the address of the last element of the queue.
Insertion and deletions are performed at rear and front end respectively. If front and rear both are NULL, it indicates that the queue is empty.
The linked representation of queue is shown in the following figure.
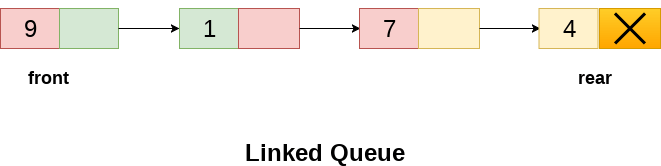
Operation on Linked Queue
There are two basic operations which can be implemented on the linked queues. The operations are Insertion and Deletion.
Insert operation
The insert operation append the queue by adding an element to the end of the queue. The new element will be the last element of the queue.
Firstly, allocate the memory for the new node ptr by using the following statement.
- Ptr = (struct node *) malloc (sizeof(struct node));
There can be the two scenario of inserting this new node ptr into the linked queue.
In the first scenario, we insert element into an empty queue. In this case, the condition front = NULL becomes true. Now, the new element will be added as the only element of the queue and the next pointer of front and rear pointer both, will point to NULL.
- Ptr -> data = item;
- If(front == NULL)
- {
- Front = ptr;
- Rear = ptr;
- Front -> next = NULL;
- Rear -> next = NULL;
- }
In the second case, the queue contains more than one element. The condition front = NULL becomes false. In this scenario, we need to update the end pointer rear so that the next pointer of rear will point to the new node ptr. Since, this is a linked queue, hence we also need to make the rear pointer point to the newly added node ptr. We also need to make the next pointer of rear point to NULL.
- Rear -> next = ptr;
- Rear = ptr;
- Rear->next = NULL;
In this way, the element is inserted into the queue. The algorithm and the C implementation is given as follows.
Algorithm
- Step 1: Allocate the space for the new node PTR
- Step 2: SET PTR -> DATA = VAL
- Step 3: IF FRONT = NULL
SET FRONT = REAR = PTR
SET FRONT -> NEXT = REAR -> NEXT = NULL
ELSE
SET REAR -> NEXT = PTR
SET REAR = PTR
SET REAR -> NEXT = NULL
[END OF IF] - Step 4: END
C Function
- Void insert(struct node *ptr, int item; )
- {
- Ptr = (struct node *) malloc (sizeof(struct node));
- If(ptr == NULL)
- {
- Printf("\nOVERFLOW\n");
- Return;
- }
- Else
- {
- Ptr -> data = item;
- If(front == NULL)
- {
- Front = ptr;
- Rear = ptr;
- Front -> next = NULL;
- Rear -> next = NULL;
- }
- Else
- {
- Rear -> next = ptr;
- Rear = ptr;
- Rear->next = NULL;
- }
- }
- }
Deletion
Deletion operation removes the element that is first inserted among all the queue elements. Firstly, we need to check either the list is empty or not. The condition front == NULL becomes true if the list is empty, in this case , we simply write underflow on the console and make exit.
Otherwise, we will delete the element that is pointed by the pointer front. For this purpose, copy the node pointed by the front pointer into the pointer ptr. Now, shift the front pointer, point to its next node and free the node pointed by the node ptr. This is done by using the following statements.
- Ptr = front;
- Front = front -> next;
- Free(ptr);
The algorithm and C function is given as follows.
Algorithm
- Step 1: IF FRONT = NULL
Write " Underflow "
Go to Step 5
[END OF IF] - Step 2: SET PTR = FRONT
- Step 3: SET FRONT = FRONT -> NEXT
- Step 4: FREE PTR
- Step 5: END
C Function
- Void delete (struct node *ptr)
- {
- If(front == NULL)
- {
- Printf("\nUNDERFLOW\n");
- Return;
- }
- Else
- {
- Ptr = front;
- Front = front -> next;
- Free(ptr);
- }
- }
Menu-Driven Program implementing all the operations on Linked Queue
- #include<stdio.h>
- #include<stdlib.h>
- Struct node
- {
- Int data;
- Struct node *next;
- };
- Struct node *front;
- Struct node *rear;
- Void insert();
- Void delete();
- Void display();
- Void main ()
- {
- Int choice;
- While(choice != 4)
- {
- Printf("\n*************************Main Menu*****************************\n");
- Printf("\n=================================================================\n");
- Printf("\n1.insert an element\n2.Delete an element\n3.Display the queue\n4.Exit\n");
- Printf("\nEnter your choice ?");
- Scanf("%d",& choice);
- Switch(choice)
- {
- Case 1:
- Insert();
- Break;
- Case 2:
- Delete();
- Break;
- Case 3:
- Display();
- Break;
- Case 4:
- Exit(0);
- Break;
- Default:
- Printf("\nEnter valid choice??\n");
- }
- }
- }
- Void insert()
- {
- Struct node *ptr;
- Int item;
- Ptr = (struct node *) malloc (sizeof(struct node));
- If(ptr == NULL)
- {
- Printf("\nOVERFLOW\n");
- Return;
- }
- Else
- {
- Printf("\nEnter value?\n");
- Scanf("%d",&item);
- Ptr -> data = item;
- If(front == NULL)
- {
- Front = ptr;
- Rear = ptr;
- Front -> next = NULL;
- Rear -> next = NULL;
- }
- Else
- {
- Rear -> next = ptr;
- Rear = ptr;
- Rear->next = NULL;
- }
- }
- }
- Void delete ()
- {
- Struct node *ptr;
- If(front == NULL)
- {
- Printf("\nUNDERFLOW\n");
- Return;
- }
- Else
- {
- Ptr = front;
- Front = front -> next;
- Free(ptr);
- }
- }
- Void display()
- {
- Struct node *ptr;
- Ptr = front;
- If(front == NULL)
- {
- Printf("\nEmpty queue\n");
- }
- Else
- { printf("\nprinting values .....\n");
- While(ptr != NULL)
- {
- Printf("\n%d\n",ptr -> data);
- Ptr = ptr -> next;
- }
- }
- }
Output:
***********Main Menu**********
==============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?1
Enter value?
123
***********Main Menu**********
==============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?1
Enter value?
90
***********Main Menu**********
==============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?3
Printing values .....
123
90
***********Main Menu**********
==============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?2
***********Main Menu**********
==============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?3
Printing values .....
90
***********Main Menu**********
==============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?4
Deletions and insertions can only be performed at front and rear end respectively, as far as linear queue is concerned.
Consider the queue shown in the following figure.
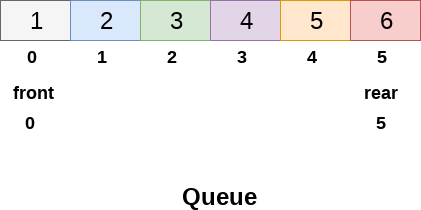
The Queue shown in above figure is completely filled and there can't be inserted any more element due to the condition rear == max - 1 becomes true.
However, if we delete 2 elements at the front end of the queue, we still can not insert any element since the condition rear = max -1 still holds.
This is the main problem with the linear queue, although we have space available in the array, but we can not insert any more element in the queue. This is simply the memory wastage and we need to overcome this problem.
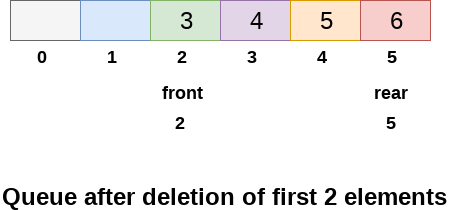
One of the solution of this problem is circular queue. In the circular queue, the first index comes right after the last index. You can think of a circular queue as shown in the following figure.
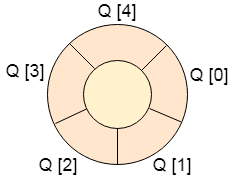
Circular queue will be full when front = -1 and rear = max-1. Implementation of circular queue is similar to that of a linear queue. Only the logic part that is implemented in the case of insertion and deletion is different from that in a linear queue.
Complexity
Time Complexity
Front | O(1) |
Rear | O(1) |
EnQueue() | O(1) |
DeQueue() | O(1) |
Insertion in Circular queue
There are three scenario of inserting an element in a queue.
- If (rear + 1)%maxsize = front, the queue is full. In that case, overflow occurs and therefore, insertion can not be performed in the queue.
- If rear != max - 1, then rear will be incremented to the mod(maxsize) and the new value will be inserted at the rear end of the queue.
- If front != 0 and rear = max - 1, then it means that queue is not full therefore, set the value of rear to 0 and insert the new element there.
Algorithm to insert an element in circular queue
- Step 1: IF (REAR+1)%MAX = FRONT
Write " OVERFLOW "
Goto step 4
[End OF IF] - Step 2: IF FRONT = -1 and REAR = -1
SET FRONT = REAR = 0
ELSE IF REAR = MAX - 1 and FRONT ! = 0
SET REAR = 0
ELSE
SET REAR = (REAR + 1) % MAX
[END OF IF] - Step 3: SET QUEUE[REAR] = VAL
- Step 4: EXIT
C Function
- Void insert(int item, int queue[])
- {
- If((rear+1)%maxsize == front)
- {
- Printf("\nOVERFLOW");
- Return;
- }
- Else if(front == -1 && rear == -1)
- {
- Front = 0;
- Rear = 0;
- }
- Else if(rear == maxsize -1 && front != 0)
- {
- Rear = 0;
- }
- Else
- {
- Rear = (rear+1)%maxsize;
- }
- Queue[rear] = item;
- }
Algorithm to delete an element from a circular queue
To delete an element from the circular queue, we must check for the three following conditions.
- If front = -1, then there are no elements in the queue and therefore this will be the case of an underflow condition.
- If there is only one element in the queue, in this case, the condition rear = front holds and therefore, both are set to -1 and the queue is deleted completely.
- If front = max -1 then, the value is deleted from the front end the value of front is set to 0.
- Otherwise, the value of front is incremented by 1 and then delete the element at the front end.
Algorithm
- Step 1: IF FRONT = -1
Write " UNDERFLOW "
Goto Step 4
[END of IF] - Step 2: SET VAL = QUEUE[FRONT]
- Step 3: IF FRONT = REAR
SET FRONT = REAR = -1
ELSE
IF FRONT = MAX -1
SET FRONT = 0
ELSE
SET FRONT = FRONT + 1
[END of IF]
[END OF IF] - Step 4: EXIT
C Function
- Void delete()
- {
- If(front == -1 & rear == -1)
- {
- Printf("\nUNDERFLOW\n");
- Return;
- }
- Else if(front == rear)
- {
- Front = -1;
- Rear = -1;
- }
- Else if(front == maxsize -1)
- {
- Front = 0;
- }
- Else
- Front = front + 1;
- }
Menu-Driven program implementing all the operations on a circular queue
- #include<stdio.h>
- #include<stdlib.h>
- #define maxsize 5
- Void insert();
- Void delete();
- Void display();
- Int front = -1, rear = -1;
- Int queue[maxsize];
- Void main ()
- {
- Int choice;
- While(choice != 4)
- {
- Printf("\n*************************Main Menu*****************************\n");
- Printf("\n=================================================================\n");
- Printf("\n1.insert an element\n2.Delete an element\n3.Display the queue\n4.Exit\n");
- Printf("\nEnter your choice ?");
- Scanf("%d",&choice);
- Switch(choice)
- {
- Case 1:
- Insert();
- Break;
- Case 2:
- Delete();
- Break;
- Case 3:
- Display();
- Break;
- Case 4:
- Exit(0);
- Break;
- Default:
- Printf("\nEnter valid choice??\n");
- }
- }
- }
- Void insert()
- {
- Int item;
- Printf("\nEnter the element\n");
- Scanf("%d",&item);
- If((rear+1)%maxsize == front)
- {
- Printf("\nOVERFLOW");
- Return;
- }
- Else if(front == -1 && rear == -1)
- {
- Front = 0;
- Rear = 0;
- }
- Else if(rear == maxsize -1 && front != 0)
- {
- Rear = 0;
- }
- Else
- {
- Rear = (rear+1)%maxsize;
- }
- Queue[rear] = item;
- Printf("\nValue inserted ");
- }
- Void delete()
- {
- Int item;
- If(front == -1 & rear == -1)
- {
- Printf("\nUNDERFLOW\n");
- Return;
- }
- Else if(front == rear)
- {
- Front = -1;
- Rear = -1;
- }
- Else if(front == maxsize -1)
- {
- Front = 0;
- }
- Else
- Front = front + 1;
- }
- Void display()
- {
- Int i;
- If(front == -1)
- Printf("\nCircular Queue is Empty!!!\n");
- Else
- {
- i = front;
- Printf("\nCircular Queue Elements are : \n");
- If(front <= rear){
- While(i <= rear)
- Printf("%d %d %d\n",queue[i++],front,rear);
- }
- Else{
- While(i <= maxsize - 1)
- Printf("%d %d %d\n", queue[i++],front,rear);
- i = 0;
- While(i <= rear)
- Printf("%d %d %d\n",queue[i++],front,rear);
- }
- }
- }
Output:
**********Main Menu**********
=============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?1
Enter the element
1
Value inserted
**********Main Menu**********
=============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?1
Enter the element
2
Value inserted
**********Main Menu**********
=============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?1
Enter the element
3
Value inserted
**********Main Menu**********
=============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?3
Circular Queue Elements are :
1
2
3
**********Main Menu**********
=============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?2
**********Main Menu**********
=============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?1
Enter the element
4
Value inserted
**********Main Menu**********
=============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?3
Circular Queue Elements are :
2
3
4
**********Main Menu**********
=============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?1
Enter the element
1
OVERFLOW
**********Main Menu**********
=============================
1.insert an element
2.Delete an element
3.Display the queue
4.Exit
Enter your choice ?
4
Deque or Double Ended Queue is a type of queue in which insertion and removal of elements can be performed from either from the front or rear. Thus, it does not follow FIFO rule (First In First Out).
Representation of Deque
Types of Deque
- Input Restricted Deque
In this deque, input is restricted at a single end but allows deletion at both the ends. - Output Restricted Deque
In this deque, output is restricted at a single end but allows insertion at both the ends.
Operations on a Deque
Below is the circular array implementation of deque. In a circular array, if the array is full, we start from the beginning.
But in a linear array implementation, if the array is full, no more elements can be inserted. In each of the operations below, if the array is full, "overflow message" is thrown.
Before performing the following operations, these steps are followed.
- Take an array (deque) of size n.
- Set two pointers at the first position and set front = -1 and rear = 0.
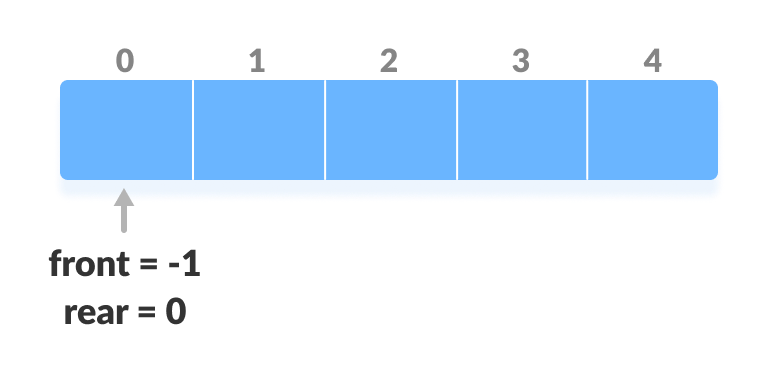Initialize an array and pointers for deque
1. Insert at the Front
This operation adds an element at the front.
- Check the position of front.
- Check the position of front
- If front < 1, reinitialize front = n-1 (last index).
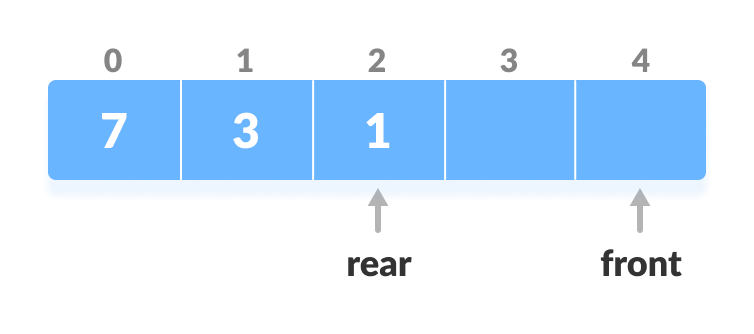
- Shift front to the end
- Else, decrease front by 1.
- Add the new key 5 into array[front].
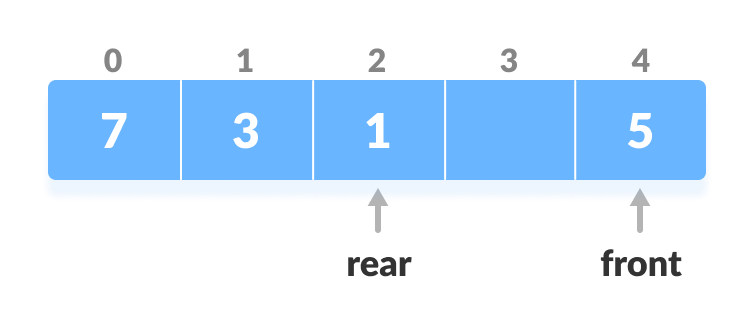Insert the element at Front
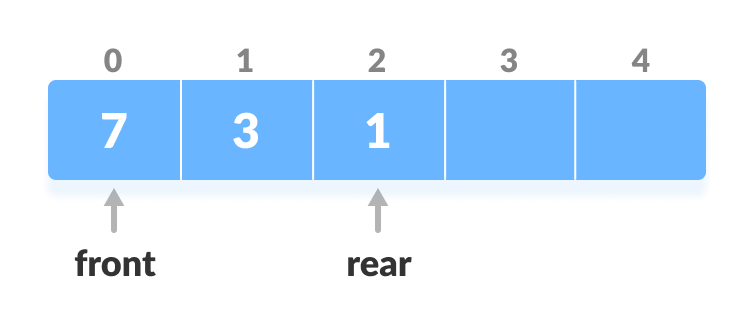
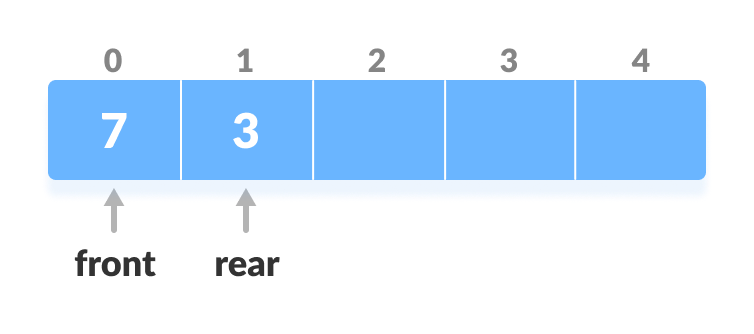
2. Insert at the Rear
This operation adds an element to the rear.
- Check if the array is full.
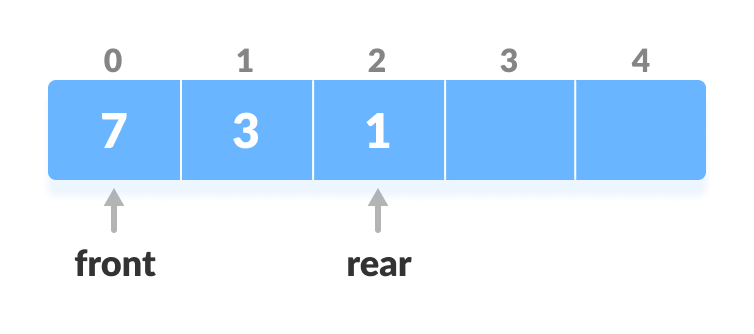Check if deque is full - If the deque is full, reinitialize rear = 0.
- Else, increase rear by 1.
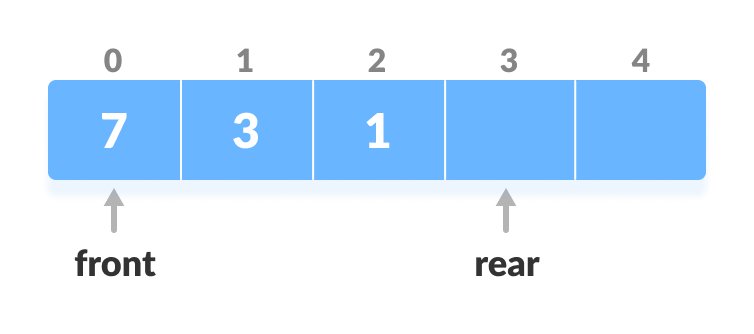Increase the rear - Add the new key 5 into array[rear].
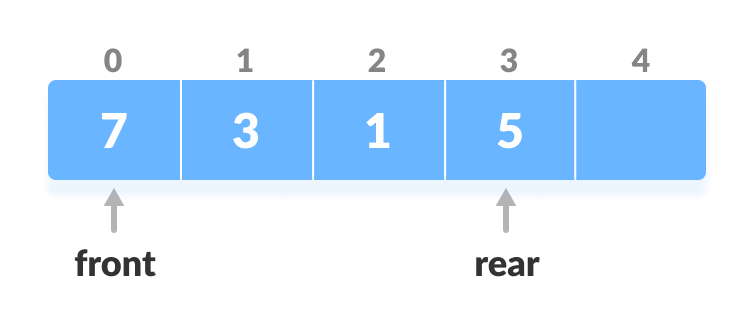
- Insert the element at rear
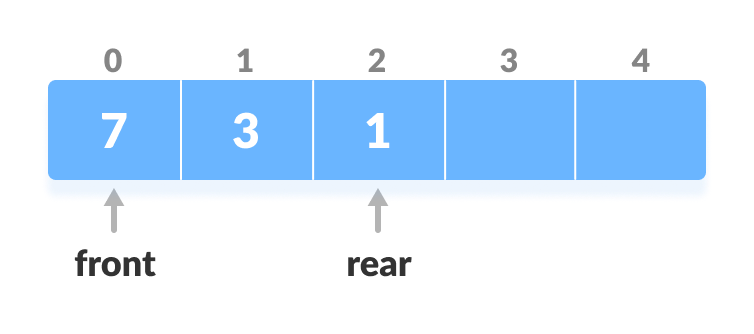
3. Delete from the Front
The operation deletes an element from the front.
- Check if the deque is empty.
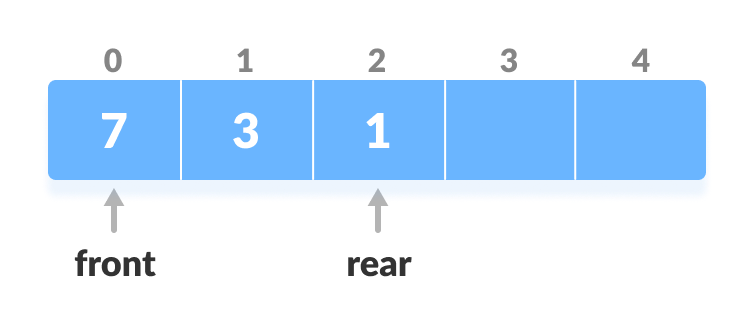
- Check if deque is empty
- If the deque is empty (i.e. front = -1), deletion cannot be performed (underflow condition).
- If the deque has only one element (i.e. front = rear), set front = -1 and rear = -1.
- Else if front is at the end (i.e. front = n - 1), set go to the front front = 0.
- Else, front = front + 1.
Increase the front
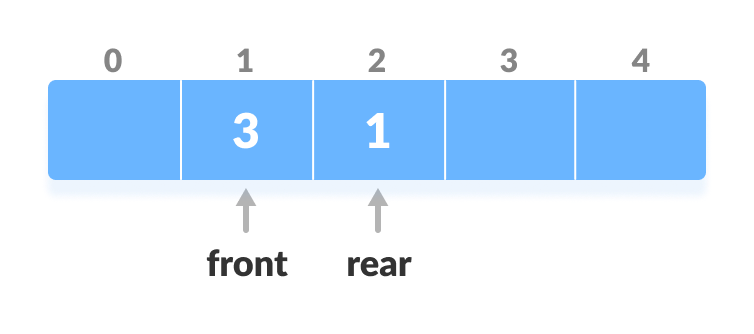
4. Delete from the Rear
This operation deletes an element from the rear.
- Check if the deque is empty.
- Check if deque is empty
- If the deque is empty (i.e. front = -1), deletion cannot be performed (underflow condition).
- If the deque has only one element (i.e. front = rear), set front = -1 and rear = -1, else follow the steps below.
- If rear is at the front (i.e. rear = 0), set go to the front rear = n - 1.
- Else, rear = rear - 1.
Decrease the rear
5. Check Empty
This operation checks if the deque is empty. If front = -1, the deque is empty.
6. Check Full
This operation checks if the deque is full. If front = 0 and rear = n - 1 OR front = rear + 1, the deque is full.
Deque Implementation in Python, Java, C, and C++
# Deque implementaion in python
Class Deque:
Def __init__(self):
Self.items = []
Def isEmpty(self):
Return self.items == []
Def addFront(self, item):
Self.items.append(item)
Def addRear(self, item):
Self.items.insert(0, item)
Def removeFront(self):
Return self.items.pop()
Def removeRear(self):
Return self.items.pop(0)
Def size(self):
Return len(self.items)
d = Deque()
Print(d.isEmpty())
d.addRear(8)
d.addRear(5)
d.addFront(7)
d.addFront(10)
Print(d.size())
Print(d.isEmpty())
d.addRear(11)
Print(d.removeRear())
Print(d.removeFront())
d.addFront(55)
d.addRear(45)
Print(d.items)
Time Complexity
The time complexity of all the above operations is constant i.e. O(1).
Applications of Deque Data Structure
- In undo operations on software.
- To store history in browsers.
- For implementing both stacks and queues.
A Priority Queue is different from a normal queue, because instead of being a “first-in-first-out”, values come out in order by priority. It is an abstract data type that captures the idea of a container whose elements have “priorities” attached to them. An element of highest priority always appears at the front of the queue. If that element is removed, the next highest priority element advances to the front.
A priority queue is typically implemented using Heap data structure.
Applications:
Dijkstra’s Shortest Path Algorithm using priority queue: When the graph is stored in the form of adjacency list or matrix, priority queue can be used to extract minimum efficiently when implementing Dijkstra’s algorithm.
Prim’s algorithm: It is used to implement Prim’s Algorithm to store keys of nodes and extract minimum key node at every step.
Data compression: It is used in Huffman codes which is used to compresses data.
Artificial Intelligence: A* Search Algorithm: The A* search algorithm finds the shortest path between two vertices of a weighted graph, trying out the most promising routes first. The priority queue (also known as the fringe) is used to keep track of unexplored routes, the one for which a lower bound on the total path length is smallest is given highest priority.
Heap Sort: Heap sort is typically implemented using Heap which is an implementation of Priority Queue.
References:
1. G. A.V, PAI , “Data Structures and Algorithms “, McGraw Hill, ISBN -13: 978-0-07-066726-6
2. A. Tharp ,"File Organization and Processing", 2008 ,Willey India edition, 9788126518685
3. M. Folk, B. Zoellick, G. Riccardi, "File Structure An Object Oriented Approach with C++", Pearson Education, 2002, ISBN 81 - 7808 - 131 - 8.
4. M. Welss, “Data Structures and Algorithm Analysis in C++", 2nd edition, Pearson Education, 2002, ISBN81-7808-670-0
