Unit 6
Hashing and File Organization
Hash Table is a data structure which stores data in an associative manner. In a hash table, data is stored in an array format, where each data value has its own unique index value. Access of data becomes very fast if we know the index of the desired data.
Thus, it becomes a data structure in which insertion and search operations are very fast irrespective of the size of the data. Hash Table uses an array as a storage medium and uses hash technique to generate an index where an element is to be inserted or is to be located from.
Hashing
Hashing is a technique to convert a range of key values into a range of indexes of an array. We're going to use modulo operator to get a range of key values. Consider an example of hash table of size 20, and the following items are to be stored. Item are in the (key,value) format.
- (1,20)
- (2,70)
- (42,80)
- (4,25)
- (12,44)
- (14,32)
- (17,11)
- (13,78)
- (37,98)
Sr.No. | Key | Hash | Array Index |
1 | 1 | 1 % 20 = 1 | 1 |
2 | 2 | 2 % 20 = 2 | 2 |
3 | 42 | 42 % 20 = 2 | 2 |
4 | 4 | 4 % 20 = 4 | 4 |
5 | 12 | 12 % 20 = 12 | 12 |
6 | 14 | 14 % 20 = 14 | 14 |
7 | 17 | 17 % 20 = 17 | 17 |
8 | 13 | 13 % 20 = 13 | 13 |
9 | 37 | 37 % 20 = 17 | 17 |
Linear Probing
As we can see, it may happen that the hashing technique is used to create an already used index of the array. In such a case, we can search the next empty location in the array by looking into the next cell until we find an empty cell. This technique is called linear probing.
Sr.No. | Key | Hash | Array Index | After Linear Probing, Array Index |
1 | 1 | 1 % 20 = 1 | 1 | 1 |
2 | 2 | 2 % 20 = 2 | 2 | 2 |
3 | 42 | 42 % 20 = 2 | 2 | 3 |
4 | 4 | 4 % 20 = 4 | 4 | 4 |
5 | 12 | 12 % 20 = 12 | 12 | 12 |
6 | 14 | 14 % 20 = 14 | 14 | 14 |
7 | 17 | 17 % 20 = 17 | 17 | 17 |
8 | 13 | 13 % 20 = 13 | 13 | 13 |
9 | 37 | 37 % 20 = 17 | 17 | 18 |
Basic Operations
Following are the basic primary operations of a hash table.
- Search − Searches an element in a hash table.
- Insert − inserts an element in a hash table.
- Delete − Deletes an element from a hash table.
DataItem
Define a data item having some data and key, based on which the search is to be conducted in a hash table.
Struct DataItem {
Int data;
Int key;
};
Hash Method
Define a hashing method to compute the hash code of the key of the data item.
Int hashCode(int key){
Return key % SIZE;
}
Search Operation
Whenever an element is to be searched, compute the hash code of the key passed and locate the element using that hash code as index in the array. Use linear probing to get the element ahead if the element is not found at the computed hash code.
Example
Struct DataItem *search(int key) {
//get the hash
Int hashIndex = hashCode(key);
//move in array until an empty
While(hashArray[hashIndex] != NULL) {
If(hashArray[hashIndex]->key == key)
Return hashArray[hashIndex];
//go to next cell
++hashIndex;
//wrap around the table
HashIndex %= SIZE;
}
Return NULL;
}
Insert Operation
Whenever an element is to be inserted, compute the hash code of the key passed and locate the index using that hash code as an index in the array. Use linear probing for empty location, if an element is found at the computed hash code.
Example
Void insert(int key,int data) {
Struct DataItem *item = (struct DataItem*) malloc(sizeof(struct DataItem));
Item->data = data;
Item->key = key;
//get the hash
Int hashIndex = hashCode(key);
//move in array until an empty or deleted cell
While(hashArray[hashIndex] != NULL && hashArray[hashIndex]->key != -1) {
//go to next cell
++hashIndex;
//wrap around the table
HashIndex %= SIZE;
}
HashArray[hashIndex] = item;
}
Delete Operation
Whenever an element is to be deleted, compute the hash code of the key passed and locate the index using that hash code as an index in the array. Use linear probing to get the element ahead if an element is not found at the computed hash code. When found, store a dummy item there to keep the performance of the hash table intact.
Example
Struct DataItem* delete(struct DataItem* item) {
Int key = item->key;
//get the hash
Int hashIndex = hashCode(key);
//move in array until an empty
While(hashArray[hashIndex] !=NULL) {
If(hashArray[hashIndex]->key == key) {
Struct DataItem* temp = hashArray[hashIndex];
//assign a dummy item at deleted position
HashArray[hashIndex] = dummyItem;
Return temp;
}
//go to next cell
++hashIndex;
//wrap around the table
HashIndex %= SIZE;
}
Return NULL;
}
Hash Table is a data structure which stores data in an associative manner. In hash table, the data is stored in an array format where each data value has its own unique index value. Access of data becomes very fast, if we know the index of the desired data.
Implementation in C
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define SIZE 20
Struct DataItem {
Int data;
Int key;
};
Struct DataItem* hashArray[SIZE];
Struct DataItem* dummyItem;
Struct DataItem* item;
Int hashCode(int key) {
Return key % SIZE;
}
Struct DataItem *search(int key) {
//get the hash
Int hashIndex = hashCode(key);
//move in array until an empty
While(hashArray[hashIndex] != NULL) {
If(hashArray[hashIndex]->key == key)
Return hashArray[hashIndex];
//go to next cell
++hashIndex;
//wrap around the table
HashIndex %= SIZE;
}
Return NULL;
}
Void insert(int key,int data) {
Struct DataItem *item = (struct DataItem*) malloc(sizeof(struct DataItem));
Item->data = data;
Item->key = key;
//get the hash
Int hashIndex = hashCode(key);
//move in array until an empty or deleted cell
While(hashArray[hashIndex] != NULL && hashArray[hashIndex]->key != -1) {
//go to next cell
++hashIndex;
//wrap around the table
HashIndex %= SIZE;
}
HashArray[hashIndex] = item;
}
Struct DataItem* delete(struct DataItem* item) {
Int key = item->key;
//get the hash
Int hashIndex = hashCode(key);
//move in array until an empty
While(hashArray[hashIndex] != NULL) {
If(hashArray[hashIndex]->key == key) {
Struct DataItem* temp = hashArray[hashIndex];
//assign a dummy item at deleted position
HashArray[hashIndex] = dummyItem;
Return temp;
}
//go to next cell
++hashIndex;
//wrap around the table
HashIndex %= SIZE;
}
Return NULL;
}
Void display() {
Int i = 0;
For(i = 0; i<SIZE; i++) {
If(hashArray[i] != NULL)
Printf(" (%d,%d)",hashArray[i]->key,hashArray[i]->data);
Else
Printf(" ~~ ");
}
Printf("\n");
}
Int main() {
DummyItem = (struct DataItem*) malloc(sizeof(struct DataItem));
DummyItem->data = -1;
DummyItem->key = -1;
Insert(1, 20);
Insert(2, 70);
Insert(42, 80);
Insert(4, 25);
Insert(12, 44);
Insert(14, 32);
Insert(17, 11);
Insert(13, 78);
Insert(37, 97);
Display();
Item = search(37);
If(item != NULL) {
Printf("Element found: %d\n", item->data);
} else {
Printf("Element not found\n");
}
Delete(item);
Item = search(37);
If(item != NULL) {
Printf("Element found: %d\n", item->data);
} else {
Printf("Element not found\n");
}
}
If we compile and run the above program, it will produce the following result −
Output
~~ (1,20) (2,70) (42,80) (4,25) ~~ ~~ ~~ ~~ ~~ ~~ ~~ (12,44) (13,78) (14,32) ~~ ~~ (17,11) (37,97) ~~
Element found: 97
Element not found
Searching Techniques-
In data structures,
- There are several searching techniques like linear search, binary search, search trees etc.
- In these techniques, time taken to search any particular element depends on the total number of elements.
Example-
- Linear search takes O(n) time to perform the search in unsorted arrays consisting of n elements.
- Binary Search takes O(logn) time to perform the search in sorted arrays consisting of n elements.
- It takes O(logn) time to perform the search in BST consisting of n elements.
Drawback-
The main drawback of these techniques is-
- As the number of elements increases, time taken to perform the search also increases.
- This becomes problematic when total number of elements become too large.
Hashing in Data Structure-
In data structures,
- Hashing is a well-known technique to search any particular element among several elements.
- It minimizes the number of comparisons while performing the search.
Advantage-
Unlike other searching techniques,
- Hashing is extremely efficient.
- The time taken by it to perform the search does not depend upon the total number of elements.
- It completes the search with constant time complexity O(1).
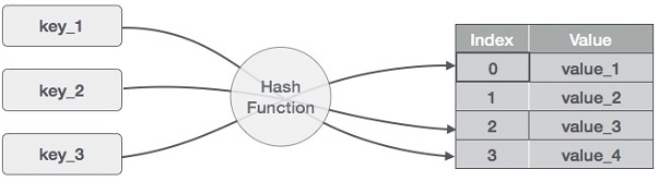
Hashing Mechanism-
In hashing,
- An array data structure called as Hash table is used to store the data items.
- Based on the hash key value, data items are inserted into the hash table.
Hash Key Value-
- Hash key value is a special value that serves as an index for a data item.
- It indicates where the data item should be be stored in the hash table.
- Hash key value is generated using a hash function.
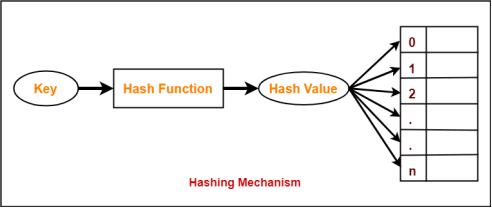
Hash Function-
Hash function is a function that maps any big number or string to a small integer value. |
Hash function takes the data item as an input and returns a small integer value as an output.
The small integer value is called as a hash value.
Hash value of the data item is then used as an index for storing it into the hash table.
Types of Hash Functions-
There are various types of hash functions available such as-
- Mid Square Hash Function
- Division Hash Function
- Folding Hash Function etc
It depends on the user which hash function he wants to use.
Properties of Hash Function-
The properties of a good hash function are-
- It is efficiently computable.
- It minimizes the number of collisions.
- It distributes the keys uniformly over the table.
Hash Function
Hash Function is used to index the original value or key and then used later each time the data associated with the value or key is to be retrieved. Thus, hashing is always a one-way operation. There is no need to "reverse engineer" the hash function by analyzing the hashed values.
Characteristics of Good Hash Function:
- The hash value is fully determined by the data being hashed.
- The hash Function uses all the input data.
- The hash function "uniformly" distributes the data across the entire set of possible hash values.
- The hash function generates complicated hash values for similar strings.
Some Popular Hash Function is:
1. Division Method:
Choose a number m smaller than the number of n of keys in k (The number m is usually chosen to be a prime number or a number without small divisors, since this frequently a minimum number of collisions).
The hash function is:

For Example: if the hash table has size m = 12 and the key is k = 100, then h (k) = 4. Since it requires only a single division operation, hashing by division is quite fast.
2. Multiplication Method:
The multiplication method for creating hash functions operates in two steps. First, we multiply the key k by a constant A in the range 0 < A < 1 and extract the fractional part of kA. Then, we increase this value by m and take the floor of the result.
The hash function is:
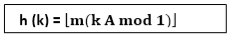
Where "k A mod 1" means the fractional part of k A, that is, k A -⌊k A⌋.
3. Mid Square Method:
The key k is squared. Then function H is defined by
- H (k) = L
Where L is obtained by deleting digits from both ends of k2. We emphasize that the same position of k2 must be used for all of the keys.
4. Folding Method:
The key k is partitioned into a number of parts k1, k2.... kn where each part except possibly the last, has the same number of digits as the required address.
Then the parts are added together, ignoring the last carry.
H (k) = k1+ k2+.....+kn
Example: Company has 68 employees, and each is assigned a unique four- digit employee number. Suppose L consist of 2- digit addresses: 00, 01, and 02....99. We apply the above hash functions to each of the following employee numbers:
- 3205, 7148, 2345
(a) Division Method: Choose a Prime number m close to 99, such as m =97, Then
- H (3205) = 4, H (7148) = 67, H (2345) = 17.
That is dividing 3205 by 17 gives a remainder of 4, dividing 7148 by 97 gives a remainder of 67, dividing 2345 by 97 gives a remainder of 17.
(b) Mid-Square Method:
k = 3205 7148 2345
k2= 10272025 51093904 5499025
h (k) = 72 93 99
Observe that fourth & fifth digits, counting from right are chosen for hash address.
(c) Folding Method: Divide the key k into 2 parts and adding yields the following hash address:
- H (3205) = 32 + 50 = 82 H (7148) = 71 + 84 = 55
- H (2345) = 23 + 45 = 68
Hashing is the transformation of a string of character into a usually shorter fixed-length value or key that represents the original string.
Hashing is used to index and retrieve items in a database because it is faster to find the item using the shortest hashed key than to find it using the original value. It is also used in many encryption algorithms.
A hash code is generated by using a key, which is a unique value.
Hashing is a technique in which given key field value is converted into the address of storage location of the record by applying the same operation on it.
The advantage of hashing is that allows the execution time of basic operation to remain constant even for the larger side.
Why we need Hashing?
Suppose we have 50 employees, and we have to give 4 digit key to each employee (as for security), and we want after entering a key, direct user map to a particular position where data is stored.
If we give the location number according to 4 digits, we will have to reserve 0000 to 9999 addresses because anybody can use anyone as a key. There is a lot of wastage.
In order to solve this problem, we use hashing which will produce a smaller value of the index of the hash table corresponding to the key of the user.
Universal Hashing
Let H be a finite collection of hash functions that map a given universe U of keys into the range {0, 1..... m-1}. Such a collection is said to be universal if for each pair of distinct keys k,l∈U, the number of hash functions h∈ H for which h(k)= h(l) is at most |H|/m. In other words, with a hash function randomly chosen from H, the chance of a collision between distinct keys k and l is no more than the chance 1/m of a collision if h(k) and h(l)were randomly and independently chosen from the set {0,1,...m-1}.
Rehashing
If any stage the hash table becomes nearly full, the running time for the operations of will start taking too much time, insert operation may fail in such situation, the best possible solution is as follows:
- Create a new hash table double in size.
- Scan the original hash table, compute new hash value and insert into the new hash table.
- Free the memory occupied by the original hash table.
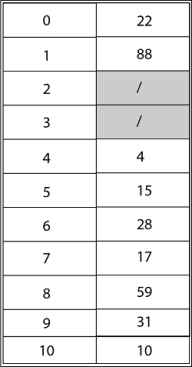
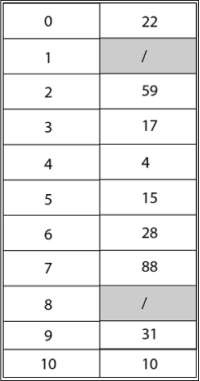
Example: Consider inserting the keys 10, 22, 31,4,15,28,17,88 and 59 into a hash table of length m = 11 using open addressing with the primary hash function h' (k) = k mod m .Illustrate the result of inserting these keys using linear probing, using quadratic probing with c1=1 and c2=3, and using double hashing with h2(k) = 1 + (k mod (m-1)).
Solution: Using Linear Probing the final state of hash table would be:
Using Quadratic Probing with c1=1, c2=3, the final state of hash table would be h (k, i) = (h' (k) +c1*i+ c2 *i2) mod m where m=11 and h' (k) = k mod m.
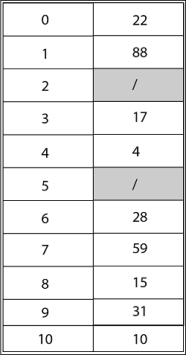
Using Double Hashing, the final state of the hash table would be:
Collision in Hashing-
In hashing,
- Hash function is used to compute the hash value for a key.
- Hash value is then used as an index to store the key in the hash table.
- Hash function may return the same hash value for two or more keys.
When the hash value of a key maps to an already occupied bucket of the hash table, It is called as a Collision. |
Collision Resolution Techniques-
Collision Resolution Techniques are the techniques used for resolving or handling the collision. |
Collision resolution techniques are classified as-
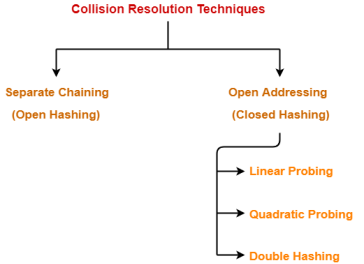
- Separate Chaining
- Open Addressing
Separate Chaining-
To handle the collision,
- This technique creates a linked list to the slot for which collision occurs.
- The new key is then inserted in the linked list.
- These linked lists to the slots appear like chains.
- That is why, this technique is called as separate chaining.
Time Complexity-
For Searching-
- In worst case, all the keys might map to the same bucket of the hash table.
- In such a case, all the keys will be present in a single linked list.
- Sequential search will have to be performed on the linked list to perform the search.
- So, time taken for searching in worst case is O(n).
For Deletion-
- In worst case, the key might have to be searched first and then deleted.
- In worst case, time taken for searching is O(n).
- So, time taken for deletion in worst case is O(n).
Load Factor (α)-
Load factor (α) is defined as-

If Load factor (α) = constant, then time complexity of Insert, Search, Delete = Θ(1)
PRACTICE PROBLEM BASED ON SEPARATE CHAINING-
Problem-
Using the hash function ‘key mod 7’, insert the following sequence of keys in the hash table-
50, 700, 76, 85, 92, 73 and 101
Use separate chaining technique for collision resolution.
Solution-
The given sequence of keys will be inserted in the hash table as-
Step-01:
- Draw an empty hash table.
- For the given hash function, the possible range of hash values is [0, 6].
- So, draw an empty hash table consisting of 7 buckets as-

Step-02:
- Insert the given keys in the hash table one by one.
- The first key to be inserted in the hash table = 50.
- Bucket of the hash table to which key 50 maps = 50 mod 7 = 1.
- So, key 50 will be inserted in bucket-1 of the hash table as-

Step-03
- The next key to be inserted in the hash table = 700.
- Bucket of the hash table to which key 700 maps = 700 mod 7 = 0.
- So, key 700 will be inserted in bucket-0 of the hash table as-
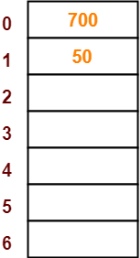
Step-04:
- The next key to be inserted in the hash table = 76.
- Bucket of the hash table to which key 76 maps = 76 mod 7 = 6.
- So, key 76 will be inserted in bucket-6 of the hash table as-

Step-05:
- The next key to be inserted in the hash table = 85.
- Bucket of the hash table to which key 85 maps = 85 mod 7 = 1.
- Since bucket-1 is already occupied, so collision occurs.
- Separate chaining handles the collision by creating a linked list to bucket-1.
- So, key 85 will be inserted in bucket-1 of the hash table as-
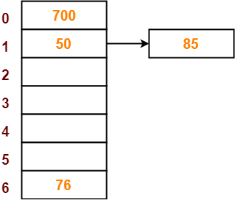
Step-06:
- The next key to be inserted in the hash table = 92.
- Bucket of the hash table to which key 92 maps = 92 mod 7 = 1.
- Since bucket-1 is already occupied, so collision occurs.
- Separate chaining handles the collision by creating a linked list to bucket-1.
- So, key 92 will be inserted in bucket-1 of the hash table as-
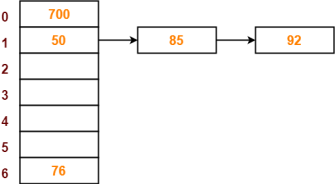
Step-07:
- The next key to be inserted in the hash table = 73.
- Bucket of the hash table to which key 73 maps = 73 mod 7 = 3.
- So, key 73 will be inserted in bucket-3 of the hash table as-
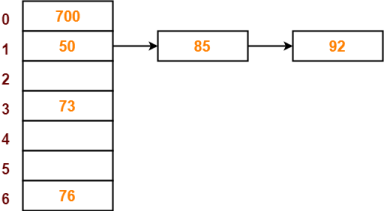
Step-08:
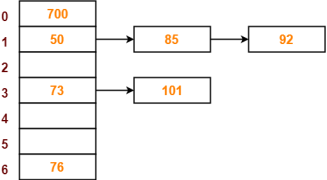
- The next key to be inserted in the hash table = 101.
- Bucket of the hash table to which key 101 maps = 101 mod 7 = 3.
- Since bucket-3 is already occupied, so collision occurs.
- Separate chaining handles the collision by creating a linked list to bucket-3.
- So, key 101 will be inserted in bucket-3 of the hash table as-
Unless your list is static and you have created a perfect hashing function, there will be collisions. SO, every hashing algorithm must have a way of dealing with collisions. A function that has a large number of collisions is said to exhibit primary clustering. A probe is an access to a distinct location (i.e. one look into the list).
Linear Probing: (also called progressive overflow) one of the simplest
- scan the file in a circular fashion, placing the synonym in the next available location
- simple, easy to maintain but not very efficient
- searching for a key not found could result in a search through the entire file (!)
- one improvement involves a 2-pass load: load all (first) records to their proper hashed locations and the second pass loads the synonyms.
- tends to produce primary clustering
Linear Quotient: (also called double hashing) similar to progressive overflow but it uses a variable increment rather than one to go to the next location
- when you have a synonym, hash again to get the next location (use a different function)
- the next synonym can use the same second function again or one modified by the number of synonyms (this tends to randomize better: sometimes called quadratic probing)
- a potential problem to look out for: it is possible to think we have searched the entire file and found it full when actually we have simply skipped over available spaces. Can avoid this by keeping track of the number of locations searched.
Variation: truncate the data (eg. Use the last digit) and use that as your step value
Separate Overflow Area (cellar): set aside a separate area for overflow records
- remember to have the hashing function generate addresses only for the primary area.
Synonym Chaining: (also called Chained Progressive Overflow) use pointers to connect synonyms
- needs an extra field but search length is cut dramatically for keys not found
- PROBLEM: needs to know that it will always be able to find a key by starting at its home address. This can only be done with two-pass loading or a separate overflow area. If we have an existing chain that uses someone else's home address, a record search that correctly started at that address would end up following the wrong chain.
Coalesced Hashing: (variation called Direct Chaining): Uses synonym chaining but when a key hashes to a location that is already used by one that is NOT a synonym it is added to the end of the current tenant's chain. This method finds the next available address by looking from the bottom up by convention. There are many choices for how to build the chain and choose the locations of overflow records:
- LISCH (late insertion standard coalesced hashing) - at the end
- LICH (last insertion) - at the end using the cellar
- EISCH (early insertion.....) - at the beginning
- EICH (early insertion - with a cellar)
- REISCH (R for random) - choosing a random location for the overflow record
- BEISCH (B for bi-directional ) - Look up first then down, then up, then down, etc.
- Direct Chaining (DCWC - direct chaining without coalescing) moving records not stored at their home address.
Computed Chaining: (DYNAMIC COLLISION RESOLUTION - keys can be moved once stored) Compute the location of the next key in the chain : this has the advantage of not using a big extra field.
- Instead of storing the actual address as the link, store a pseudolink.
- What is stored is the chain length count. We use this value to compute the needed address. The advantages: we need to store only a small value so 'pointer size' is small and we no longer need to retrieve the intermediate values to get the one we need.
- This method avoids coalescing by moving records found at someone else's home address. Uses the key actually stored at the probe address to compute the next probe address and not the key being stored or retrieved.
The Algorithm:
- Hash the key of the record to be inserted to obtain the home address for storing the record.
- If the home address is empty, insert the record at that location.
- If the record is a duplicate, terminate with a "duplicate record" message.
- If the term stored at the hashed location is not at its home address, move it to the next empty location found by stepping through the table using the increment associated with its predecessor element, and then insert the incoming record into the hashed location, else
- Locate the end of the probe chain and in the process, check for a duplicate record.
- Use the increment associated with the last item in the probe chain to find an empty location for the incoming record. In the process, check for a full table.
- Set the pseudolink at the position of the predecessor record to connect to the empty location.
- Insert the record in the empty location.
Brent's Method: Dynamic collision resolution
- Assumes any record can be moved if it becomes convenient. Justify additional processing because we usually insert an item only once but will want to retrieve it many times.
- Primary Probe Chain is the sequence of locations visited during the insertion or retrieval of a record.
- Involves moving a record if we want to put some other record there - so we can store a record at its home address - we move the one that shouldn't be there.
- The Secondary Probe Chain is the one we follow when trying to move a record from the primary probe chain.
The Algorithm:
- Hash the key of the record to be inserted to obtain the home address for storing the record.
- If the home address is empty, insert the record at that location, else
- Compute the next potential address for storing the incoming record. Initialize S <= 2.
- While potential storage address is not empty,
- Check if it is the home address. If it is, the table is full, terminate with a "full table" message.
- If the record stored at the potential storage address is the same as the incoming record, terminate with a "duplicate record" message.
- Compute the next potential address for storing the incoming record. Set S <= S + 1.
/* Attempt to move a record previously inserted */
- Initialize i <= 1 and j <= 1.
- While (I + J < S)
- Determine if the record stored at the ith position on the primary probe chain can be moved j offsets along its secondary probe chain.
- If it can be moved, then
- Move it and insert the incoming record into the vacated position I along its primary probe chain; terminate with a successful insertion, else
- Vary I and/or j to minimize the sum of (j + I); if I = j, minimize on i.
/* Moving has failed */
- Insert the incoming record at position s on its primary probe chain; terminate with a successful insertion.
Progressive values of i and j as search along primary and secondary probe chains progresses. In order to be a viable move, sum(i,j) must be less than S (S is the chain length for the incoming record if nothing is moved). i is the position of a placed record along the primary probe chain and j is the length of this placed record's probe chain should we decide to move it (i.e. the secondary probe chain). The general idea is to reduce the total of the chain lengths by re-arranging keys.
i | 1 | 1 | 2 | 1 | 2 | 3 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 5 |
j | 1 | 2 | 1 | 3 | 2 | 1 | 4 | 3 | 2 | 1 | 5 | 4 | 3 | 2 | 1 |
Sum(i,j) | 2 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 6 | 6 | 6 | 6 | 6 |
Binary Trees: If Brent's method is good, can we get better? How about a binary decision tree? At each point in the process there are essentially two choices: continue to the next address along the probe chain or move the item being stored. Left branch means continue; and Right branch means move. The tree here is used as a control structure - not to store data. The tree is generated in a breadth first fashion (like the nodes in a heap sort).
- The Algorithm:
- Hash the key of the record to be inserted to obtain the home address for storing the record.
- If the home address is empty, insert the record at that location, else
- Until an empty location or a "full" table is encountered,
- Generate a binary tree control structure in a breadth first left t right fashion. The address of the Ichild of a node is determined by adding (I) the increment associated with the key of the record coming in to the node to (ii) the current address. The address of the rchild of a node is determined by adding (I) the increment associated with the key of the record stored in the node to (ii) the current address.
- At the leftmost node on each level, check against the record associated with it for a duplicate record. If found, terminate with a "duplicate record" message.
- If a "full table", terminate with a "full table" message.
- If an empty node is found, the path from the empty node back to the root determines which records, if any, need to be moved. Each right link signifies that a relocation is necessary. First set the current node pointer to the last node generated in the binary tree and set the empty location pointer to the table address associated with the last node generated.
- Until the current pointer equals the root node of the binary tree (bottom up), note the type of branch from the parent of the current node to the current node.
- On a right branch, move the record stored at the location contained in the parent node into the location indicated by the empty location pointer. Set the empty location pointer to the newly vacated position and make the parent node the current node.
- On a left branch, make the parent node the current node.
- Insert the record coming into the root position into the empty location. Terminate with a successful insertion.
- Until an empty location or a "full" table is encountered,
Summary : Collision Resolution
Static Methods: (keys, once placed, don't move)
Linear Probing: (Open Addressing) Simplest; find next available location for record using linear search
Variation: 2-pass load with Linear Probing for synonyms only
Double Hashing: (Open Addressing) use second function to find the next location ('randomize' offset)
Variation 1: use H2[K] for second hash, then revert to Linear Probing if that fails
Variation 2: use H2[K] to generate step-size rather than new address
Synonym Chaining: (Chained Overflow/ Single Hash) use pointer to connect synonyms; cuts down # probes required to find; first value must be at home address
Coalesced Hashing: (Chained/ Single Hash) add record to end of current chain; don't need first value at home address
Dynamic Methods: (any key can be moved if it becomes advantageous to do so)
Direct Chaining: (Chained/ Single Hash) Dynamic variant of Coalesced Chaining: if placed key is not at it's home address, remove it and all other keys after it in its chain; place incoming key and re-insert those that were removed.
Computed Chaining: (Chained/ Double Hash) store # of links rather than actual address; move records not at their home address; always use i-value of last record in chain to compute step value (i.e. step value changes at each link)
Brent's Method: (Open Addressing/ Double Hash) move any record if we will achieve a net gain (always use step value of incoming/searched for key; doesn't use additional pointer space)
Binary Tree Insertion: (Open Addressing Double Hash) move any record(s) to achieve a net gain (always use step value of incoming/searched for key; doesn't use additional pointer space)
Algorithm | Static/ Dynamic | Addressing Method | 1- or 2-Pass Load | Type of Link | Single/Double Hash Functions | Key used by H2[K] |
Linear Probing | Static | Open | 1 | n/a | Single | n/a |
Double Hashing | Static | Open | 1 | n/a | Double (2 types) | Type 1: incoming, new address Type 2: incoming, step size |
Chained Overflow | Static | Chained | 2 | Actual link | Single | n/a |
Coalesced Hashing | Static | Chained | 1 | Actual link | Single | n/a |
Computed Chaining | Dynamic | Chained | 1 | Pseudolink | Double | Resident (last value in chain) |
Brent's Method | Dynamic | Open | 1 | n/a | Double | Incoming |
Binary Tree Insertion | Dynamic | Open | 1 | n/a | Double | Incoming |
In this section we will see what quadratic probing technique is in open addressing scheme. There is an ordinary hash function h’(x) : U → {0, 1, . . ., m – 1}. In open addressing scheme, the actual hash function h(x) is taking the ordinary hash function h’(x) and attach some another part with it to make one quadratic equation.
h´ = (𝑥) = 𝑥 𝑚𝑜𝑑 𝑚
ℎ(𝑥, 𝑖) = (ℎ´(𝑥) + 𝑖2)𝑚𝑜𝑑 𝑚
We can put some other quadratic equations also using some constants
The value of i = 0, 1, . . ., m – 1. So we start from i = 0, and increase this until we get one free space. So initially when i = 0, then the h(x, i) is same as h´(x).
Example
We have a list of size 20 (m = 20). We want to put some elements in linear probing fashion. The elements are {96, 48, 63, 29, 87, 77, 48, 65, 69, 94, 61}

Hash Table

For insertion of a key(K) – value(V) pair into a hash map, 2 steps are required:
- K is converted into a small integer (called its hash code) using a hash function.
- The hash code is used to find an index (hashCode % arrSize) and the entire linked list at that index(Separate chaining) is first searched for the presence of the K already.
- If found, it’s value is updated and if not, the K-V pair is stored as a new node in the list.
Complexity and Load Factor
- For the first step, time taken depends on the K and the hash function.
For example, if the key is a string “abcd”, then it’s hash function may depend on the length of the string. But for very large values of n, the number of entries into the map, length of the keys is almost negligible in comparison to n so hash computation can be considered to take place in constant time, i.e, O(1). - For the second step, traversal of the list of K-V pairs present at that index needs to be done. For this, the worst case may be that all the n entries are at the same index. So, time complexity would be O(n). But, enough research has been done to make hash functions uniformly distribute the keys in the array so this almost never happens.
- So, on an average, if there are n entries and b is the size of the array there would be n/b entries on each index. This value n/b is called the load factor that represents the load that is there on our map.
- This Load Factor needs to be kept low, so that number of entries at one index is less and so is the complexity almost constant, i.e., O(1).
Rehashing:
As the name suggests, rehashing means hashing again. Basically, when the load factor increases to more than its pre-defined value (default value of load factor is 0.75), the complexity increases. So to overcome this, the size of the array is increased (doubled) and all the values are hashed again and stored in the new double sized array to maintain a low load factor and low complexity.
Why rehashing?
Rehashing is done because whenever key value pairs are inserted into the map, the load factor increases, which implies that the time complexity also increases as explained above. This might not give the required time complexity of O(1).
Hence, rehash must be done, increasing the size of the bucketArray so as to reduce the load factor and the time complexity.
How Rehashing is done?
Rehashing can be done as follows:
- For each addition of a new entry to the map, check the load factor.
- If it’s greater than its pre-defined value (or default value of 0.75 if not given), then Rehash.
- For Rehash, make a new array of double the previous size and make it the new bucketarray.
- Then traverse to each element in the old bucketArray and call the insert() for each so as to insert it into the new larger bucket array.
Program to implement Rehashing:
// Java program to implement Rehashing
Import java.util.ArrayList;
Class Map<K, V> {
Class MapNode<K, V> {
K key; V value; MapNode<K, V> next;
Public MapNode(K key, V value) { This.key = key; This.value = value; Next = null; } }
// The bucket array where // the nodes containing K-V pairs are stored ArrayList<MapNode<K, V> > buckets;
// No. Of pairs stored - n Int size;
// Size of the bucketArray - b Int numBuckets;
// Default loadFactor Final double DEFAULT_LOAD_FACTOR = 0.75;
Public Map() { NumBuckets = 5;
Buckets = new ArrayList<>(numBuckets);
For (int i = 0; i < numBuckets; i++) { // Initialising to null Buckets.add(null); } System.out.println("HashMap created"); System.out.println("Number of pairs in the Map: " + size); System.out.println("Size of Map: " + numBuckets); System.out.println("Default Load Factor : " + DEFAULT_LOAD_FACTOR + " "); }
Private int getBucketInd(K key) {
// Using the inbuilt function from the object class Int hashCode = key.hashCode();
// array index = hashCode%numBuckets Return (hashCode % numBuckets); }
Public void insert(K key, V value) { // Getting the index at which it needs to be inserted Int bucketInd = getBucketInd(key);
// The first node at that index MapNode<K, V> head = buckets.get(bucketInd);
// First, loop through all the nodes present at that index // to check if the key already exists While (head != null) {
// If already present the value is updated If (head.key.equals(key)) { Head.value = value; Return; } Head = head.next; }
// new node with the K and V MapNode<K, V> newElementNode = new MapNode<K, V>(key, value);
// The head node at the index Head = buckets.get(bucketInd);
// the new node is inserted // by making it the head // and it's next is the previous head NewElementNode.next = head;
Buckets.set(bucketInd, newElementNode);
System.out.println("Pair(" + key + ", " + value + ") inserted successfully. ");
// Incrementing size // as new K-V pair is added to the map Size++;
// Load factor calculated Double loadFactor = (1.0 * size) / numBuckets;
System.out.println("Current Load factor = " + loadFactor);
// If the load factor is > 0.75, rehashing is done If (loadFactor > DEFAULT_LOAD_FACTOR) { System.out.println(loadFactor + " is greater than " + DEFAULT_LOAD_FACTOR); System.out.println("Therefore Rehashing will be done. ");
// Rehash Rehash();
System.out.println("New Size of Map: " + numBuckets + " "); }
System.out.println("Number of pairs in the Map: " + size); System.out.println("Size of Map: " + numBuckets + " "); }
Private void rehash() {
System.out.println(" ***Rehashing Started*** ");
// The present bucket list is made temp ArrayList<MapNode<K, V> > temp = buckets;
// New bucketList of double the old size is created Buckets = new ArrayList<MapNode<K, V> >(2 * numBuckets);
For (int i = 0; i < 2 * numBuckets; i++) { // Initialised to null Buckets.add(null); } // Now size is made zero // and we loop through all the nodes in the original bucket list(temp) // and insert it into the new list Size = 0; NumBuckets *= 2;
For (int i = 0; i < temp.size(); i++) {
// head of the chain at that index MapNode<K, V> head = temp.get(i);
While (head != null) { K key = head.key; V val = head.value;
// calling the insert function for each node in temp // as the new list is now the bucketArray Insert(key, val); Head = head.next; } }
System.out.println(" ***Rehashing Ended*** "); }
Public void printMap() {
// The present bucket list is made temp ArrayList<MapNode<K, V> > temp = buckets;
System.out.println("Current HashMap:"); // loop through all the nodes and print them For (int i = 0; i < temp.size(); i++) {
// head of the chain at that index MapNode<K, V> head = temp.get(i);
While (head != null) { System.out.println("key = " + head.key + ", val = " + head.value);
Head = head.next; } } System.out.println(); } }
Public class GFG {
Public static void main(String[] args) {
// Creating the Map Map<Integer, String> map = new Map<Integer, String>();
// Inserting elements Map.insert(1, "Geeks"); Map.printMap();
Map.insert(2, "forGeeks"); Map.printMap();
Map.insert(3, "A"); Map.printMap();
Map.insert(4, "Computer"); Map.printMap();
Map.insert(5, "Portal"); Map.printMap(); } } |
Output:
HashMap created
Number of pairs in the Map: 0
Size of Map: 5
Default Load Factor : 0.75
Pair(1, Geeks) inserted successfully.
Current Load factor = 0.2
Number of pairs in the Map: 1
Size of Map: 5
Current HashMap:
Key = 1, val = Geeks
Pair(2, forGeeks) inserted successfully.
Current Load factor = 0.4
Number of pairs in the Map: 2
Size of Map: 5
Current HashMap:
Key = 1, val = Geeks
Key = 2, val = forGeeks
Pair(3, A) inserted successfully.
Current Load factor = 0.6
Number of pairs in the Map: 3
Size of Map: 5
Current HashMap:
Key = 1, val = Geeks
Key = 2, val = forGeeks
Key = 3, val = A
Pair(4, Computer) inserted successfully.
Current Load factor = 0.8
0.8 is greater than 0.75
Therefore Rehashing will be done.
***Rehashing Started***
Pair(1, Geeks) inserted successfully.
Current Load factor = 0.1
Number of pairs in the Map: 1
Size of Map: 10
Pair(2, forGeeks) inserted successfully.
Current Load factor = 0.2
Number of pairs in the Map: 2
Size of Map: 10
Pair(3, A) inserted successfully.
Current Load factor = 0.3
Number of pairs in the Map: 3
Size of Map: 10
Pair(4, Computer) inserted successfully.
Current Load factor = 0.4
Number of pairs in the Map: 4
Size of Map: 10
***Rehashing Ended***
New Size of Map: 10
Number of pairs in the Map: 4
Size of Map: 10
Current HashMap:
Key = 1, val = Geeks
Key = 2, val = forGeeks
Key = 3, val = A
Key = 4, val = Computer
Pair(5, Portal) inserted successfully.
Current Load factor = 0.5
Number of pairs in the Map: 5
Size of Map: 10
Current HashMap:
Key = 1, val = Geeks
Key = 2, val = forGeeks
Key = 3, val = A
Key = 4, val = Computer
Key = 5, val = Portal
Explanation : In collision handling method chaining is a concept which introduces an additional field with data i.e. chain. A separate chain table is maintained for colliding data. When collision occurs, we store the second colliding data by linear probing method. The address of this colliding data can be stored with the first colliding element in the chain table, without replacement.
For example, consider elements:
131, 3, 4, 21, 61, 6, 71, 8, 9
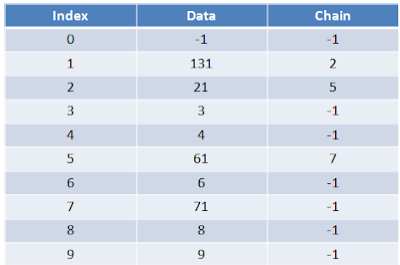
From the example, you can see that the chain is maintained from the number who demands for location 1. First number 131 comes, we place it at index 1. Next comes 21, but collision occurs so by linear probing we will place 21 at index 2, and chain is maintained by writing 2 in chain table at index 1. Similarly next comes 61, by linear probing we can place 61 at index 5 and chain will maintained at index 2. Thus any element which gives hash key as 1 will be stored by linear probing at empty location but a chain is maintained so that traversing the hash table will be efficient.
/************************************************************************
Program to create hash table and to handle the collision using chaining
Without replacement.In this program hash function is (number %10)
*************************************************************************/
#include<iostream.h>
#include<conio.h>
#include<stdlib.h>
#define MAX 10
Class WO_chain
{
Private:
Int a[MAX][2];
Public:
WO_chain();
Int create(int);
Void chain(int,int),display();
};
/*
--------------------------------------------------------------------------
The constructor defined
--------------------------------------------------------------------------
*/
WO_chain::WO_chain()
{
Int i;
For(i=0;i<MAX;i++)
{
a[i][0]=-1;
a[i][1]=-1;
}
}
/*
--------------------------------------------------------------------------
The create function is for generating the hash key
Input:the num means the number which we want to place in the hash table
Output:returns the hash key
Calls:none
Called By:main
--------------------------------------------------------------------------
*/
Int WO_chain::create(int num)
{
Int key;
Key=num%10;
Return key;
}
/*
--------------------------------------------------------------------------
The chain function handles the collision without replacement of numbers
Input:the num,hash key and hash table by array a[]
Output:none
Calls:none
Called By:main
--------------------------------------------------------------------------
*/
Void WO_chain::chain(int key,int num)
{
Int flag,i,count=0,ch;
Flag=0;
//checking full condition
i=0;
While(i<MAX)
{
If(a[i][0]!=-1)
Count++;
i++;
}
If(count==MAX)
{
Cout<<"\nHash Table Is Full";
Display();
Getch();
Exit(1);
}
//placing number otherwise
If(a[key][0]==-1)//no collision case
a[key][0]=num;
Else //if collision occurs
{
Ch=a[key][1];//taking the chain
//If only one number in hash table with current obtained key
If(ch==-1)
{
For(i=key+1;i<MAX;i++)//performing linear probing
{
If(a[i][0]==-1) //at immediate empty slot
{
a[i][0]=num;//placiing number
a[key][1]=i; //setting the chain
Flag=1;
Break;
}
}
}
//if many numbers are already in the hash table
//we will find the next empty slot to place number
Else
{
While((a[ch][0]!=-1)&&(a[ch][1]!=-1))//traversing thro chain till empty slot is found*/
Ch=a[ch][1];
For(i=ch+1;i<MAX;i++)
{
If(a[i][0]==-1)
{
a[i][0]=num;//placing the number
a[ch][1]=i; //setting chain
Flag=1;
Break;
}
}
}
//If the numbers are occupied somewhere from middle and are stored upto
//the MAX then we will search for the empty slot upper half of the array
If(flag!=1)
{
If(ch==-1)
{
For(i=0;i<key;i++)//performing linear probing
{
If(a[i][0]==-1) //at immediate empty slot
{
a[i][0]=num;//placiing number
a[key][1]=i; //setting the chain
Flag=1;
Break;
}
}
}
//if many numbers are already in the hash table
//we will find the next empty slot to place number
Else
{
//traversing thro chain till empty slot is found
While((a[ch][0]!=-1)&&(a[ch][1]!=-1))
Ch=a[ch][1];
For(i=ch+1;i<key;i++)
{
If(a[i][0]==-1)
{
a[i][0]=num;//placing the number
a[ch][1]=i; //setting chain
Flag=1;
Break;
}
}
}
}
}
}
/*
--------------------------------------------------------------------------
The display function displays the hash table and chain table
Input:hash table by array a[]
Output:none
Calls:none
Called By:main
--------------------------------------------------------------------------
*/
Void WO_chain::display()
{
Int i;
Cout<<"\n The Hash Table is...\n";
For(i=0;i<MAX;i++)
Cout<<"\n "<<i<<" "<<a[i][0]<<" "<<a[i][1];
}
/*
--------------------------------------------------------------------------
The main function
Calls:create,chain,display
Called By:O.S.
--------------------------------------------------------------------------
*/
Void main()
{
Int num,key,i;
Char ans;
WO_chain h;
Clrscr();
Cout<<"\nChaining Without Replacement";
Do
{
Cout<<"\n Enter The Number";
Cin>>num;
Key=h.create(num);//returns hash key
h.chain(key,num);//collision handled by chaining without replacement
Cout<<"\n Do U Wish To Continue?(y/n)";
Ans=getche();
}while(ans=='y');
h.display();//displays hash table
Getch();
}
Hashing with Chaining
A  data structure uses hashing with chaining to store data as an array,
data structure uses hashing with chaining to store data as an array, 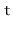 , of lists. An integer,
, of lists. An integer, 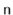 , keeps track of the total number of items in all lists (see Figure 5.1):
, keeps track of the total number of items in all lists (see Figure 5.1):
Array<List> t;
Int n;
![\includegraphics[width=\textwidth ]{figs/chainedhashtable}](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643292829_9907556.png) |
Figure 5.1: An example of a    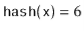 |
The hash value of a data item 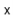 , denoted
, denoted 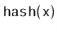 is a value in the range
is a value in the range 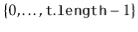 . All items with hash value
. All items with hash value 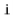 are stored in the list at
are stored in the list at ![$ \mathtt{t[i]}$](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643292830_504278.png) . To ensure that lists don't get too long, we maintain the invariant
. To ensure that lists don't get too long, we maintain the invariant
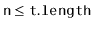
So that the average number of elements stored in one of these lists is 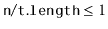 .
.
To add an element, 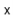 , to the hash table, we first check if the length of
, to the hash table, we first check if the length of 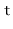 needs to be increased and, if so, we grow
needs to be increased and, if so, we grow 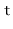 . With this out of the way we hash
. With this out of the way we hash 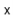 to get an integer,
to get an integer, 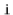 , in the range
, in the range 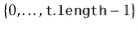 , and we append
, and we append 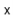 to the list
to the list ![$ \mathtt{t[i]}$](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643292831_1957617.png) :
:
Bool add(T x) {
If (find(x) != null) return false;
If (n+1 > t.length) resize();
t[hash(x)].add(x);
n++;
Return true;
}
Growing the table, if necessary, involves doubling the length of 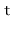 and reinserting all elements into the new table. This strategy is exactly the same as the one used in the implementation of
and reinserting all elements into the new table. This strategy is exactly the same as the one used in the implementation of 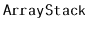 and the same result applies: The cost of growing is only constant when amortized over a sequence of insertions.
and the same result applies: The cost of growing is only constant when amortized over a sequence of insertions.
Besides growing, the only other work done when adding a new value 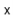 to a
to a  involves appending
involves appending 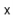 to the list
to the list ![$ \mathtt{t[hash(x)]}$](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643292831_5306158.png) .
.
To remove an element, 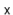 , from the hash table, we iterate over the list
, from the hash table, we iterate over the list ![$ \mathtt{t[hash(x)]}$](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643292831_626611.png) until we find
until we find 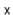 so that we can remove it:
so that we can remove it:
T remove(T x) {
Int j = hash(x);
For (int i = 0; i < t[j].size(); i++) {
T y = t[j].get(i);
If (x == y) {
t[j].remove(i);
n--;
Return y;
}
}
Return null;
}
This takes 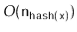 time, where
time, where 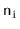 denotes the length of the list stored at
denotes the length of the list stored at ![$ \mathtt{t[i]}$](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643292831_8963554.png) .
.
Searching for the element 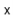 in a hash table is similar. We perform a linear search on the list
in a hash table is similar. We perform a linear search on the list ![$ \mathtt{t[hash(x)]}$](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643292832_0363796.png) :
:
T find(T x) {
Int j = hash(x);
For (int i = 0; i < t[j].size(); i++)
If (x == t[j].get(i))
Return t[j].get(i);
Return null;
}
Again, this takes time proportional to the length of the list ![$ \mathtt{t[hash(x)]}$](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643292832_0944526.png) .
.
The performance of a hash table depends critically on the choice of the hash function. A good hash function will spread the elements evenly among the 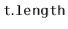 lists, so that the expected size of the list
lists, so that the expected size of the list ![$ \mathtt{t[hash(x)]}$](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643292832_219928.png) is
is 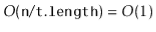 . On the other hand, a bad hash function will hash all values (including
. On the other hand, a bad hash function will hash all values (including 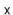 ) to the same table location, in which case the size of the list
) to the same table location, in which case the size of the list ![$ \mathtt{t[hash(x)]}$](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643292832_391313.png) will be
will be 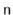 . In the next section we describe a good hash function.
. In the next section we describe a good hash function.
5.1.1 Multiplicative Hashing
Multiplicative hashing is an efficient method of generating hash values based on modular arithmetic (discussed in Section 2.3) and integer division. It uses the 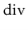 operator, which calculates the integral part of a quotient, while discarding the remainder. Formally, for any integers
operator, which calculates the integral part of a quotient, while discarding the remainder. Formally, for any integers 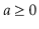 and
and 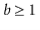 ,
, 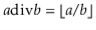 .
.
In multiplicative hashing, we use a hash table of size 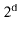 for some integer
for some integer 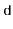 (called the dimension). The formula for hashing an integer
(called the dimension). The formula for hashing an integer 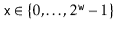 is
is
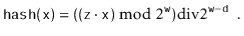
Here, 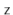 is a randomly chosen odd integer in
is a randomly chosen odd integer in 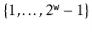 . This hash function can be realized very efficiently by observing that, by default, operations on integers are already done modulo
. This hash function can be realized very efficiently by observing that, by default, operations on integers are already done modulo 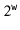 where
where 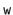 is the number of bits in an integer. (See Figure 5.2.) Furthermore, integer division by
is the number of bits in an integer. (See Figure 5.2.) Furthermore, integer division by 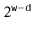 is equivalent to dropping the rightmost
is equivalent to dropping the rightmost 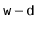 bits in a binary representation (which is implemented by shifting the bits right by
bits in a binary representation (which is implemented by shifting the bits right by 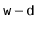 using the
using the  operator). In this way, the code that implements the above formula is simpler than the formula itself:
operator). In this way, the code that implements the above formula is simpler than the formula itself:
Int hash(T x) {
Return ((unsigned)(z * hashCode(x))) >> (w-d);
}
 |
Figure 5.2: The operation of the multiplicative hash function with 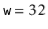 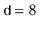 |
The following lemma, whose proof is deferred until later in this section, shows that multiplicative hashing does a good job of avoiding collisions:
Lemma 5..1 Let 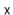 and
and 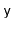 be any two values in
be any two values in 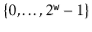 with
with 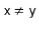 . Then
. Then 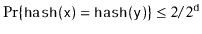 .
.
With Lemma 5.1, the performance of  , and
, and  are easy to analyze:
are easy to analyze:
Lemma 5..2 For any data value  , the expected length of the list
, the expected length of the list ![$ \mathtt{t[hash(x)]}$](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643292834_1624207.png) is at most
is at most 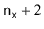 , where
, where 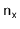 is the number of occurrences of
is the number of occurrences of 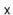 in the hash table.
in the hash table.
Proof. Let  be the (multi-)set of elements stored in the hash table that are not equal to
be the (multi-)set of elements stored in the hash table that are not equal to 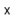 . For an element
. For an element 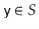 , define the indicator variable
, define the indicator variable
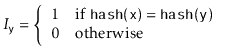
And notice that, by Lemma 5.1, ![$ \mathrm{E}[I_{\ensuremath{\mathtt{y}}}] \le
2/2^{\ensuremath{\mathtt{d}}}=2/\ensuremath{\mathtt{t.length}}$](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643292834_6839623.png) . The expected length of the list
. The expected length of the list ![$ \mathtt{t[hash(x)]}$](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643292834_753712.png) is given by
is given by
![$\displaystyle \mathrm{E}\left[\ensuremath{\mathtt{t[hash(x)].size()}}\right]$](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643292834_8020952.png)
![$\displaystyle \mathrm{E}\left[\ensuremath{\mathtt{n}}_{\ensuremath{\mathtt{x}}} + \sum_{\ensuremath{\mathtt{y}}\in S} I_{\ensuremath{\mathtt{y}}}\right]$](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643292834_903789.png)
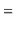
![$\displaystyle \ensuremath{\mathtt{n}}_{\ensuremath{\mathtt{x}}} + \sum_{\ensuremath{\mathtt{y}}\in S} \mathrm{E}[I_{\ensuremath{\mathtt{y}}} ]$](https://glossaread-contain.s3.ap-south-1.amazonaws.com/epub/1643292835_0222566.png)
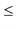
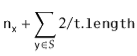
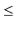
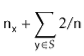
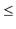
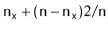
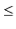
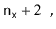
as required.
Now, we want to prove Lemma 5.1, but first we need a result from number theory. In the following proof, we use the notation 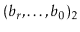 to denote
to denote 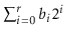 , where each
, where each 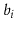 is a bit, either 0 or 1. In other words,
is a bit, either 0 or 1. In other words, 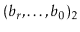 is the integer whose binary representation is given by
is the integer whose binary representation is given by 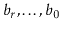 . We use
. We use  to denote a bit of unknown value.
to denote a bit of unknown value.
Lemma 5..3 Let 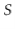 be the set of odd integers in
be the set of odd integers in 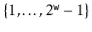 ; let
; let 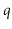 and
and 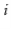 be any two elements in
be any two elements in 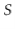 . Then there is exactly one value
. Then there is exactly one value 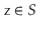 such that
such that 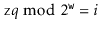 .
.
Proof. Since the number of choices for 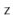 and
and 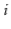 is the same, it is sufficient to prove that there is at most one value
is the same, it is sufficient to prove that there is at most one value 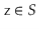 that satisfies
that satisfies 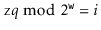 .
.
Suppose, for the sake of contradiction, that there are two such values 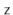 and
and 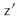 , with
, with 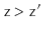 . Then
. Then
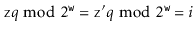
So
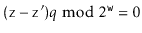
But this means that
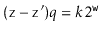 (5.1)
(5.1)
For some integer 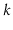 . Thinking in terms of binary numbers, we have
. Thinking in terms of binary numbers, we have
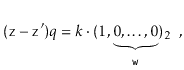
So that the 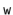 trailing bits in the binary representation of
trailing bits in the binary representation of 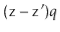 are all 0's.
are all 0's.
Furthermore 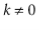 , since
, since 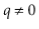 and
and 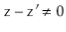 . Since
. Since 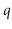 is odd, it has no trailing 0's in its binary representation:
is odd, it has no trailing 0's in its binary representation:

Since 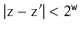 ,
, 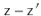 has fewer than
has fewer than 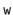 trailing 0's in its binary representation:
trailing 0's in its binary representation:
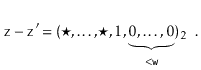
Therefore, the product 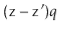 has fewer than
has fewer than 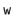 trailing 0's in its binary representation:
trailing 0's in its binary representation:
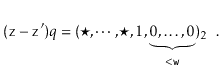
Therefore 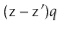 cannot satisfy (5.1), yielding a contradiction and completing the proof.
cannot satisfy (5.1), yielding a contradiction and completing the proof. 
The utility of Lemma 5.3 comes from the following observation: If 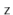 is chosen uniformly at random from
is chosen uniformly at random from 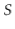 , then
, then 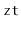 is uniformly distributed over
is uniformly distributed over 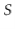 . In the following proof, it helps to think of the binary representation of
. In the following proof, it helps to think of the binary representation of 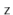 , which consists of
, which consists of 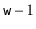 random bits followed by a 1.
random bits followed by a 1.
Proof. [Proof of Lemma 5.1] First we note that the condition 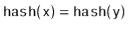 is equivalent to the statement the highest-order
is equivalent to the statement the highest-order 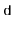 bits of
bits of 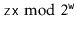 and the highest-order
and the highest-order 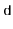 bits of
bits of 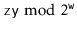 are the same.'' A necessary condition of that statement is that the highest-order
are the same.'' A necessary condition of that statement is that the highest-order 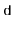 bits in the binary representation of
bits in the binary representation of 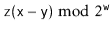 are either all 0's or all 1's. That is,
are either all 0's or all 1's. That is,
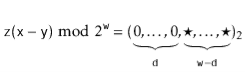 (5.2)
(5.2)
When 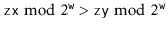 or
or
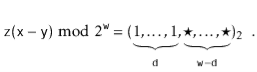 (5.3)
(5.3)
When 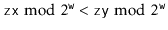 . Therefore, we only have to bound the probability that
. Therefore, we only have to bound the probability that 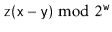 looks like (5.2) or (5.3).
looks like (5.2) or (5.3).
Let 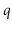 be the unique odd integer such that
be the unique odd integer such that 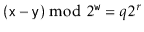 for some integer
for some integer 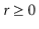 . By Lemma 5.3, the binary representation of
. By Lemma 5.3, the binary representation of 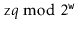 has
has 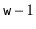 random bits, followed by a 1:
random bits, followed by a 1:
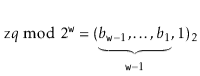
Therefore, the binary representation of 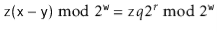 has
has 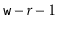 random bits, followed by a 1, followed by
random bits, followed by a 1, followed by 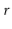 0's:
0's:
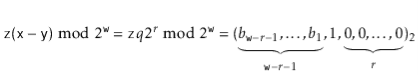
We can now finish the proof: If 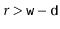 , then the
, then the 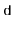 higher order bits of
higher order bits of 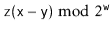 contain both 0's and 1's, so the probability that
contain both 0's and 1's, so the probability that 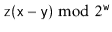 looks like (5.2) or (5.3) is 0. If
looks like (5.2) or (5.3) is 0. If 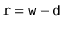 , then the probability of looking like (5.2) is 0, but the probability of looking like (5.3) is
, then the probability of looking like (5.2) is 0, but the probability of looking like (5.3) is 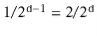 (since we must have
(since we must have 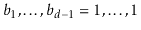 ). If
). If 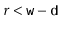 , then we must have
, then we must have 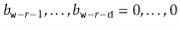 or
or 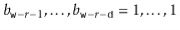 . The probability of each of these cases is
. The probability of each of these cases is 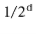 and they are mutually exclusive, so the probability of either of these cases is
and they are mutually exclusive, so the probability of either of these cases is 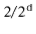 . This completes the proof.
. This completes the proof.
What is File?
File is a collection of records related to each other. The file size is limited by the size of memory and storage medium.
There are two important features of file:
1. File Activity
2. File Volatility
File activity specifies percent of actual records which proceed in a single run.
File volatility addresses the properties of record changes. It helps to increase the efficiency of disk design than tape.
File Organization
File organization ensures that records are available for processing. It is used to determine an efficient file organization for each base relation.
For example, if we want to retrieve employee records in alphabetical order of name. Sorting the file by employee name is a good file organization. However, if we want to retrieve all employees whose marks are in a certain range, a file is ordered by employee name would not be a good file organization.
Types of File Organization
There are three types of organizing the file:
1. Sequential access file organization
2. Direct access file organization
3. Indexed sequential access file organization
1. Sequential access file organization
- Storing and sorting in contiguous block within files on tape or disk is called as sequential access file organization.
- In sequential access file organization, all records are stored in a sequential order. The records are arranged in the ascending or descending order of a key field.
- Sequential file search starts from the beginning of the file and the records can be added at the end of the file.
- In sequential file, it is not possible to add a record in the middle of the file without rewriting the file.
Advantages of sequential file
- It is simple to program and easy to design.
- Sequential file is best use if storage space.
Disadvantages of sequential file
- Sequential file is time consuming process.
- It has high data redundancy.
- Random searching is not possible.
2. Direct access file organization
- Direct access file is also known as random access or relative file organization.
- In direct access file, all records are stored in direct access storage device (DASD), such as hard disk. The records are randomly placed throughout the file.
- The records does not need to be in sequence because they are updated directly and rewritten back in the same location.
- This file organization is useful for immediate access to large amount of information. It is used in accessing large databases.
- It is also called as hashing.
Advantages of direct access file organization
- Direct access file helps in online transaction processing system (OLTP) like online railway reservation system.
- In direct access file, sorting of the records are not required.
- It accesses the desired records immediately.
- It updates several files quickly.
- It has better control over record allocation.
Disadvantages of direct access file organization
- Direct access file does not provide back up facility.
- It is expensive.
- It has less storage space as compared to sequential file.
3. Indexed sequential access file organization
- Indexed sequential access file combines both sequential file and direct access file organization.
- In indexed sequential access file, records are stored randomly on a direct access device such as magnetic disk by a primary key.
- This file have multiple keys. These keys can be alphanumeric in which the records are ordered is called primary key.
- The data can be access either sequentially or randomly using the index. The index is stored in a file and read into memory when the file is opened.
Advantages of Indexed sequential access file organization
- In indexed sequential access file, sequential file and random file access is possible.
- It accesses the records very fast if the index table is properly organized.
- The records can be inserted in the middle of the file.
- It provides quick access for sequential and direct processing.
- It reduces the degree of the sequential search.
Disadvantages of Indexed sequential access file organization
- Indexed sequential access file requires unique keys and periodic reorganization.
- Indexed sequential access file takes longer time to search the index for the data access or retrieval.
- It requires more storage space.
- It is expensive because it requires special software.
- It is less efficient in the use of storage space as compared to other file organizations.
File Organization
- The File is a collection of records. Using the primary key, we can access the records. The type and frequency of access can be determined by the type of file organization which was used for a given set of records.
- File organization is a logical relationship among various records. This method defines how file records are mapped onto disk blocks.
- File organization is used to describe the way in which the records are stored in terms of blocks, and the blocks are placed on the storage medium.
- The first approach to map the database to the file is to use the several files and store only one fixed length record in any given file. An alternative approach is to structure our files so that we can contain multiple lengths for records.
- Files of fixed length records are easier to implement than the files of variable length records.
Objective of file organization
- It contains an optimal selection of records, i.e., records can be selected as fast as possible.
- To perform insert, delete or update transaction on the records should be quick and easy.
- The duplicate records cannot be induced as a result of insert, update or delete.
- For the minimal cost of storage, records should be stored efficiently.
Types of file organization:
File organization contains various methods. These particular methods have pros and cons on the basis of access or selection. In the file organization, the programmer decides the best-suited file organization method according to his requirement.
Types of file organization are as follows:
- Sequential file organization
- Heap file organization
- Hash file organization
- B+ file organization
- Indexed sequential access method (ISAM)
- Cluster file organization
Sequential File Organization
This method is the easiest method for file organization. In this method, files are stored sequentially. This method can be implemented in two ways:
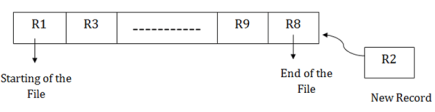
1. Pile File Method:
- It is a quite simple method. In this method, we store the record in a sequence, i.e., one after another. Here, the record will be inserted in the order in which they are inserted into tables.
- In case of updating or deleting of any record, the record will be searched in the memory blocks. When it is found, then it will be marked for deleting, and the new record is inserted.

Insertion of the new record:
Suppose we have four records R1, R3 and so on upto R9 and R8 in a sequence. Hence, records are nothing but a row in the table. Suppose we want to insert a new record R2 in the sequence, then it will be placed at the end of the file. Here, records are nothing but a row in any table.
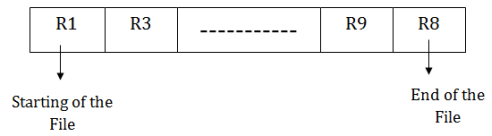
2. Sorted File Method:
- In this method, the new record is always inserted at the file's end, and then it will sort the sequence in ascending or descending order. Sorting of records is based on any primary key or any other key.
- In the case of modification of any record, it will update the record and then sort the file, and lastly, the updated record is placed in the right place.
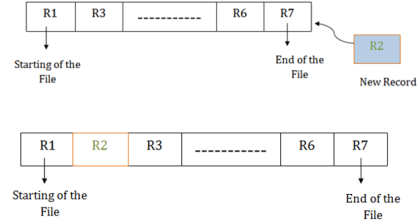
Insertion of the new record:
Suppose there is a preexisting sorted sequence of four records R1, R3 and so on upto R6 and R7. Suppose a new record R2 has to be inserted in the sequence, then it will be inserted at the end of the file, and then it will sort the sequence.
Pros of sequential file organization
- It contains a fast and efficient method for the huge amount of data.
- In this method, files can be easily stored in cheaper storage mechanism like magnetic tapes.
- It is simple in design. It requires no much effort to store the data.
- This method is used when most of the records have to be accessed like grade calculation of a student, generating the salary slip, etc.
- This method is used for report generation or statistical calculations.
Cons of sequential file organization
- It will waste time as we cannot jump on a particular record that is required but we have to move sequentially which takes our time.
- Sorted file method takes more time and space for sorting the records.
Heap file organization
- It is the simplest and most basic type of organization. It works with data blocks. In heap file organization, the records are inserted at the file's end. When the records are inserted, it doesn't require the sorting and ordering of records.
- When the data block is full, the new record is stored in some other block. This new data block need not to be the very next data block, but it can select any data block in the memory to store new records. The heap file is also known as an unordered file.
- In the file, every record has a unique id, and every page in a file is of the same size. It is the DBMS responsibility to store and manage the new records.
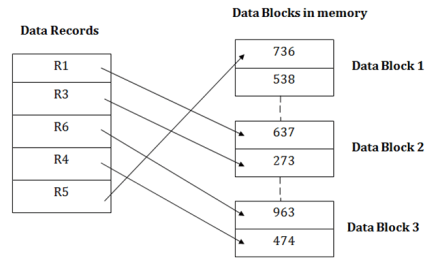
Insertion of a new record
Suppose we have five records R1, R3, R6, R4 and R5 in a heap and suppose we want to insert a new record R2 in a heap. If the data block 3 is full then it will be inserted in any of the database selected by the DBMS, let's say data block 1.
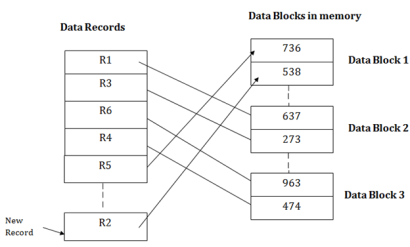
If we want to search, update or delete the data in heap file organization, then we need to traverse the data from staring of the file till we get the requested record.
If the database is very large then searching, updating or deleting of record will be time-consuming because there is no sorting or ordering of records. In the heap file organization, we need to check all the data until we get the requested record.
Pros of Heap file organization
- It is a very good method of file organization for bulk insertion. If there is a large number of data which needs to load into the database at a time, then this method is best suited.
- In case of a small database, fetching and retrieving of records is faster than the sequential record.
Cons of Heap file organization
- This method is inefficient for the large database because it takes time to search or modify the record.
- This method is inefficient for large databases.
Hash File Organization
Hash File Organization uses the computation of hash function on some fields of the records. The hash function's output determines the location of disk block where the records are to be placed.
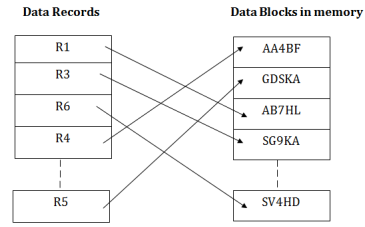
When a record has to be received using the hash key columns, then the address is generated, and the whole record is retrieved using that address. In the same way, when a new record has to be inserted, then the address is generated using the hash key and record is directly inserted. The same process is applied in the case of delete and update.
In this method, there is no effort for searching and sorting the entire file. In this method, each record will be stored randomly in the memory.
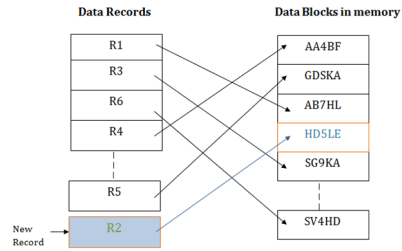
B+ File Organization
- B+ tree file organization is the advanced method of an indexed sequential access method. It uses a tree-like structure to store records in File.
- It uses the same concept of key-index where the primary key is used to sort the records. For each primary key, the value of the index is generated and mapped with the record.
- The B+ tree is similar to a binary search tree (BST), but it can have more than two children. In this method, all the records are stored only at the leaf node. Intermediate nodes act as a pointer to the leaf nodes. They do not contain any records.
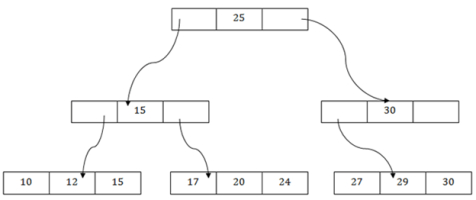
The above B+ tree shows that:
- There is one root node of the tree, i.e., 25.
- There is an intermediary layer with nodes. They do not store the actual record. They have only pointers to the leaf node.
- The nodes to the left of the root node contain the prior value of the root and nodes to the right contain next value of the root, i.e., 15 and 30 respectively.
- There is only one leaf node which has only values, i.e., 10, 12, 17, 20, 24, 27 and 29.
- Searching for any record is easier as all the leaf nodes are balanced.
- In this method, searching any record can be traversed through the single path and accessed easily.
Pros of B+ tree file organization
- In this method, searching becomes very easy as all the records are stored only in the leaf nodes and sorted the sequential linked list.
- Traversing through the tree structure is easier and faster.
- The size of the B+ tree has no restrictions, so the number of records can increase or decrease and the B+ tree structure can also grow or shrink.
- It is a balanced tree structure, and any insert/update/delete does not affect the performance of tree.
Cons of B+ tree file organization
- This method is inefficient for the static method.
Indexed sequential access method (ISAM)
ISAM method is an advanced sequential file organization. In this method, records are stored in the file using the primary key. An index value is generated for each primary key and mapped with the record. This index contains the address of the record in the file.
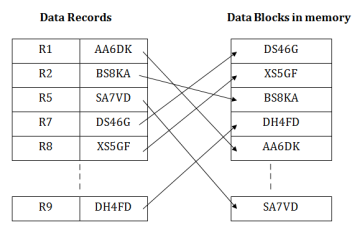
If any record has to be retrieved based on its index value, then the address of the data block is fetched and the record is retrieved from the memory.
Pros of ISAM:
- In this method, each record has the address of its data block, searching a record in a huge database is quick and easy.
- This method supports range retrieval and partial retrieval of records. Since the index is based on the primary key values, we can retrieve the data for the given range of value. In the same way, the partial value can also be easily searched, i.e., the student name starting with 'JA' can be easily searched.
Cons of ISAM
- This method requires extra space in the disk to store the index value.
- When the new records are inserted, then these files have to be reconstructed to maintain the sequence.
- When the record is deleted, then the space used by it needs to be released. Otherwise, the performance of the database will slow down.
Cluster file organization
- When the two or more records are stored in the same file, it is known as clusters. These files will have two or more tables in the same data block, and key attributes which are used to map these tables together are stored only once.
- This method reduces the cost of searching for various records in different files.
- The cluster file organization is used when there is a frequent need for joining the tables with the same condition. These joins will give only a few records from both tables. In the given example, we are retrieving the record for only particular departments. This method can't be used to retrieve the record for the entire department.
In this method, we can directly insert, update or delete any record. Data is sorted based on the key with which searching is done. Cluster key is a type of key with which joining of the table is performed.
Types of Cluster file organization:
Cluster file organization is of two types:
1. Indexed Clusters:
In indexed cluster, records are grouped based on the cluster key and stored together. The above EMPLOYEE and DEPARTMENT relationship is an example of an indexed cluster. Here, all the records are grouped based on the cluster key- DEP_ID and all the records are grouped.
2. Hash Clusters:
It is similar to the indexed cluster. In hash cluster, instead of storing the records based on the cluster key, we generate the value of the hash key for the cluster key and store the records with the same hash key value.
Pros of Cluster file organization
- The cluster file organization is used when there is a frequent request for joining the tables with same joining condition.
- It provides the efficient result when there is a 1:M mapping between the tables.
Cons of Cluster file organization
- This method has the low performance for the very large database.
- If there is any change in joining condition, then this method cannot use. If we change the condition of joining then traversing the file takes a lot of time.
- This method is not suitable for a table with a 1:1 condition.
- Indexing is used to optimize the performance of a database by minimizing the number of disk accesses required when a query is processed.
- The index is a type of data structure. It is used to locate and access the data in a database table quickly.
Index structure:
Indexes can be created using some database columns.
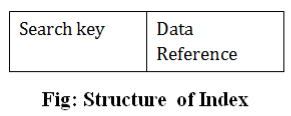
- The first column of the database is the search key that contains a copy of the primary key or candidate key of the table. The values of the primary key are stored in sorted order so that the corresponding data can be accessed easily.
- The second column of the database is the data reference. It contains a set of pointers holding the address of the disk block where the value of the particular key can be found.
Indexing Methods
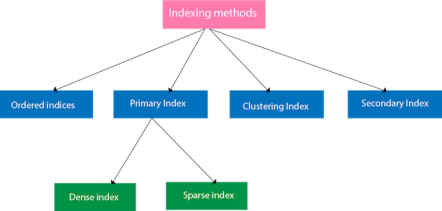
Ordered indices
The indices are usually sorted to make searching faster. The indices which are sorted are known as ordered indices.
Example: Suppose we have an employee table with thousands of record and each of which is 10 bytes long. If their IDs start with 1, 2, 3....and so on and we have to search student with ID-543.
- In the case of a database with no index, we have to search the disk block from starting till it reaches 543. The DBMS will read the record after reading 543*10=5430 bytes.
- In the case of an index, we will search using indexes and the DBMS will read the record after reading 542*2= 1084 bytes which are very less compared to the previous case.
Primary Index
- If the index is created on the basis of the primary key of the table, then it is known as primary indexing. These primary keys are unique to each record and contain 1:1 relation between the records.
- As primary keys are stored in sorted order, the performance of the searching operation is quite efficient.
- The primary index can be classified into two types: Dense index and Sparse index.
Dense index
- The dense index contains an index record for every search key value in the data file. It makes searching faster.
- In this, the number of records in the index table is same as the number of records in the main table.
- It needs more space to store index record itself. The index records have the search key and a pointer to the actual record on the disk.
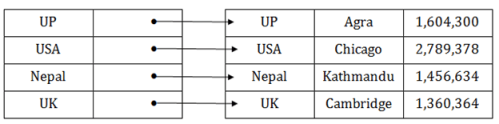
Sparse index
- In the data file, index record appears only for a few items. Each item points to a block.
- In this, instead of pointing to each record in the main table, the index points to the records in the main table in a gap.
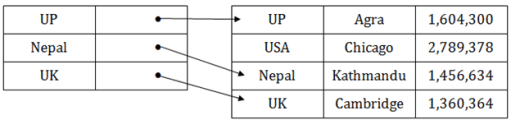
Clustering Index
- A clustered index can be defined as an ordered data file. Sometimes the index is created on non-primary key columns which may not be unique for each record.
- In this case, to identify the record faster, we will group two or more columns to get the unique value and create index out of them. This method is called a clustering index.
- The records which have similar characteristics are grouped, and indexes are created for these group.
Example: suppose a company contains several employees in each department. Suppose we use a clustering index, where all employees which belong to the same Dept_ID are considered within a single cluster, and index pointers point to the cluster as a whole. Here Dept_Id is a non-unique key.
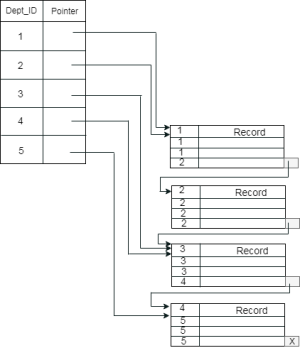
The previous schema is little confusing because one disk block is shared by records which belong to the different cluster. If we use separate disk block for separate clusters, then it is called better technique.
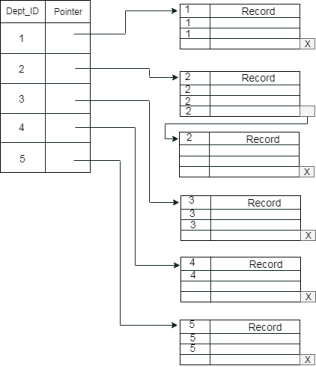
Secondary Index
In the sparse indexing, as the size of the table grows, the size of mapping also grows. These mappings are usually kept in the primary memory so that address fetch should be faster. Then the secondary memory searches the actual data based on the address got from mapping. If the mapping size grows then fetching the address itself becomes slower. In this case, the sparse index will not be efficient. To overcome this problem, secondary indexing is introduced.
In secondary indexing, to reduce the size of mapping, another level of indexing is introduced. In this method, the huge range for the columns is selected initially so that the mapping size of the first level becomes small. Then each range is further divided into smaller ranges. The mapping of the first level is stored in the primary memory, so that address fetch is faster. The mapping of the second level and actual data are stored in the secondary memory (hard disk).
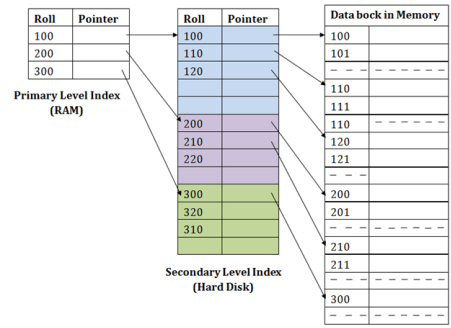
For example:
- If you want to find the record of roll 111 in the diagram, then it will search the highest entry which is smaller than or equal to 111 in the first level index. It will get 100 at this level.
- Then in the second index level, again it does max (111) <= 111 and gets 110. Now using the address 110, it goes to the data block and starts searching each record till it gets 111.
- This is how a search is performed in this method. Inserting, updating or deleting is also done in the same manner.
References:
1. G. A.V, PAI , “Data Structures and Algorithms “, McGraw Hill, ISBN -13: 978-0-07-066726-6
2. A. Tharp ,"File Organization and Processing", 2008 ,Willey India edition, 9788126518685
3. M. Folk, B. Zoellick, G. Riccardi, "File Structure An Object Oriented Approach with C++", Pearson Education, 2002, ISBN 81 - 7808 - 131 - 8.
4. M. Welss, “Data Structures and Algorithm Analysis in C++", 2nd edition, Pearson Education, 2002, ISBN81-7808-670-0