UNIT-1

Sets and Propositions

1.1 Sets (Sets, combinations of sets, Venn diagram, Finite and infinite sets, countable sets, multi-sets)

Sets- A set is a collection of well-defined objects which are called the elements or members of the set.

We generally use capital letters to denote sets and lowercase letters for elements.

If any element which exists in the set is to be denoted as-

Suppose an element ‘a’ is from a set X, then it is represented as- a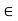X

Which means the element ‘a’ belongs to the set X.

If the element is not form the group then we use ‘not belongs to’.

Representation of sets-

There are two ways to represent sets.

1. In first way, the elements of the set are separated by comma and contained in the bracket-{  }.

2. The second way is that we define the characteristic of the element.

For example-

Suppose we have a set ‘A’ of all odd integers which are greater than 3.

Then we can represent it two ways-

1. A = {5, 7, 9…….}

2. A = {x | x is an odd integer, x>3 }

Subsets-

Let every element of set X is also an element of a set Y, then X is said to be the subset of Y.

Symbolically it is written as-

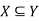
Which is read as- X is the subset of Y.

Note- If X = Y then

Proper sub-set-

A set X is called proper subset the set Y is-

1. X is subset of Y

2. Y is not subset of X

Note- every set is a subset to itself.

Equal sets-

If X and Y are two sets such that every element of X is an element of Y and every element of Y is an element of X, the set and set Y will be equal always.

We write it as X = Y and read as X and Y are identical.

Super set-

If X is a subset of Y, then Y is called a super set of X.

Null set-

A set which does not contain any element is known as null set.

We denote a null set by ∅ 

The null set is a subset of every set.

Singleton-

A set which has only one element is called singleton.

Example- A = {10} and B = {∅}

Theorem- if ∅ and ∅’ are empty sets then ∅=∅’

Proof: Let ∅≠ ∅’  then the following conditions must be true-

1. There is element x∈∅ such that x∉∅’

2. There is element x∈∅’ such that x∉∅.

but both these conditions are false since ∅’ and ∅’ has any elements if follows that ∅=∅’.

Operations on sets-

1. Union and intersection-

Union- We denote union of two sets as- A∪B, which is the set of all elements which belongs to A or to B.

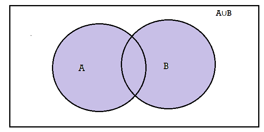
That is-

A∪B = {x | x∈∅A or x∈∅B}

Intersection- We denote intersection of two sets as- A∩B, which is the set of all elements which belongs to A and to B.

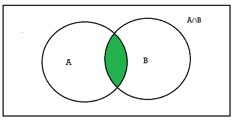
That is-

A∩B = {x | x∈∅A and x∈∅B }

Note- Two sets are said to be disjoint if they have no common elements in common.

 Example: If A = {1, 2, 3, 4, 5, 6}, B = {4, 5, 6, 7, 8, 9} and C = {5, 6, 7, 8, 9, 10}

Then-

A∪B = {1, 2, 3, 4, 5, 6, 7, 8, 9}

A∪C = {1, 2, 3, 4, 5, 6, 7, 8, 9,10}

B∪C = {4, 5, 6, 7, 8, 9, 10}

A∩B = {4, 5, 6}

A∩C = {5, 6}

B∩C = {5, 6, 7, 8, 9}

Property-1-

An element x belongs to the union A∪ B if x belongs to A or x belongs to B; hence every element

In A belongs to A ∪ B, and every element in B belongs to A ∪ B. That is,

A ⊆A ∪ B and B ⊆A ∪ B

Property-2-

An element x belongs to the union A∪ B if x belongs to A or x belongs to B; hence every element

In A belongs to A ∪ B, and every element in B belongs to A ∪ B. That is,

A ⊆A ∪ B and B ⊆A ∪ B

Complements, differences and symmetric differences-

Complement-

The complement of a set A, denoted by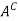 , is the set of elements which belong to U (universal set) but which do not belong to A. That is

= {x | x ∈ U, x /∈ A}

Difference-

The difference of A and B, denoted by A\B or A-B, is the set of elements which belong to A but which do not belong to B that is-

A-B = {x | x ∈ A, x / ∈ B}

The set A\B or A-B is read “A minus B”.

Symmetric difference-

The symmetric difference of sets A and B, denoted by A ⊕ B, consists of those elements which belong to A or B but not to both. That is

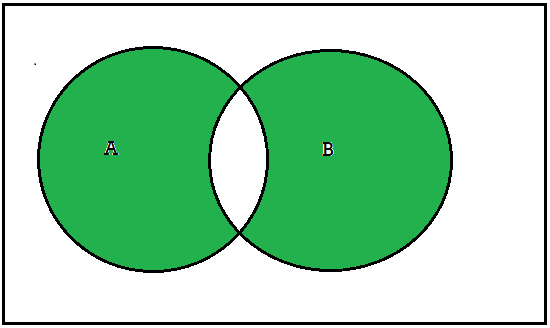
A ⊕ B = (A ∪ B)-(A ∩ B) or A ⊕ B = (A-B) ∪ (B-A)

Cardinality of sets-

If A is finite set with n distinct elements, then n is called the cardinality of A. The cardinality of A is denoted by |A| [or by n (A)].

Example: Let A = {a, b, c, d}, then A is a finite set and |A| = 4

Cardinality of union of two sets-

Number of elements in A ∪ B: (Cardinality of union) If A and B are any two finite sets then, the numbers of elements in A ∪ B, denoted by | A ∪ B | is given by | A ∪ B | = | A | + | B | − | A ∩ B |

Principal of inclusion and Exclusion-

Let we have A and B are finite sets. Then A ∪ B and A ∩ B are

Finite and

n(A ∪ B) = n(A) + n(B) − n(A ∩ B)

That is, we find the number of elements in A or B (or both) by first adding n(A) and n(B) (inclusion) and then

Subtracting n(A ∩ B) (exclusion) since its elements were counted twice

For three sets-

n(A ∪ B ∪ C) = n(A) + n(B) + n(C) − n(A ∩ B) − n(A ∩ C) − n(B ∩ C) + n(A ∩ B ∩ C)

Finite set-

If a set has finite number of elements then the set said to be a finite set.

Examples:

1. {2, 5, 9, 8, 11, 15, 19, 85}

2. The set of all vowels in English alphabets

3. The set of students in of high school in a particular school.

Infinite set-

If a set has infinite number of elements then the set said to be a infinite set.

Examples:

1. The set of all natural numbers.

2. The set of total points on a line.

Countable and uncountable sets-

A set S is said to be countable if it is either a finite set or countably infinite set.

A set is said to be uncountable otherwise.

Example-

Suppose we have a set of even natural numbers N = {2n: n∈N }. We can find a Bijection 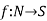with the formula 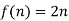. So we can say that the set is Countably infinite and also countable.

The set of odd natural numbers is also countably infinite.

Countably infinite and uncountably infinite sets-

Any set which can be put in a one-to-one correspondence with integers so that the prescription can be given for identifying its members one at a time is called a countably infinite set.

Any set which can not be put in a one-to-one correspondence with integers is said to be undoubtably infinite set.

Multi-set-

A multi-set is a generalization of a set where repetition of elements matters.

Like {4, 5, 6} and {5, 4, 6} are the same multi-set but the set {5, 5, 4, 6} is the different multi-set as there is repetition of the elements.

So that, “A multi-set is a set-like, unordered collection where multiplicity(repetition) of the elements matters.

Here multiplicity means how many times an element occurs in the set.

Notation-

If an element ‘a’ occurs ‘n’ times in a multi-set A then it can be represented as - .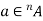

For example-

, ,

1.2 Principal of inclusion and exclusion

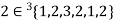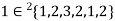The Inclusion-Exclusion principle can be stated as below-

Let A and B any two finite sets, then-

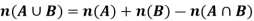
Meaning- Here if we have to find the number 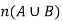of elements in the union of A and B.

So then we add n(A) and n(B) which means we are including these two.

And then we exclude .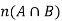

Note- For three sets-

If we have three finite sets A, B and C then-

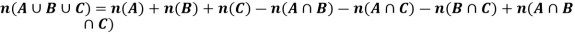
Example: Find the number of students at a college choosing at least one of the subject from mathematics, physics and statistics.

The data is given as-

65 study maths, 45 study physics, 42 study statistics

20 study maths and physics, 25 study maths and statistics, 15 study physics and statistics and 8 study all the three subjects.

Sol.

Here we need to find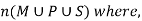

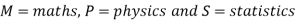
Now by using Inclusion-Exclusion principle-

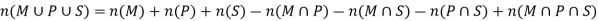
Which gives-

Therefore, we find that 100 students study at least one of the three subjects.

1.3 Mathematical induction

Mathematical induction is a mathematical technique is used to prove a statement, a theorem or a formula is true for every natural number.

The technique has two steps to prove any statement-

1. Base step (it proves that a statement is true for the initial value)

2. Inductive step (it proves that is the statement is true for n’th iteration then it is also true for 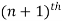iteration.

Example-1: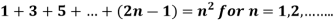

Sol. here for n = 1,     1 = 1²

Now let us assume that the statement is true for n = k

Hence we assume that 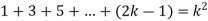is true.

Now we need to prove that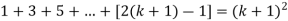

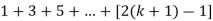
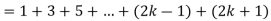
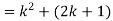
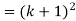
So that 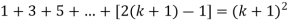which satisfies the second step.

Hence-

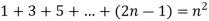
Example-2: Prove 1+2+...+n = n(n+1)/2 using a proof by induction

Sol.

Let n=1: 1 = 1(1+1)/2 = 1(2)/2 = 1 is true,

Step-1: Assume n=k holds: 1+2+...+k = k(k+1)/2

Show n=k+1 holds: 1+2+...+k+(k+1)=(k+1)((k+1)+1)/2 

Substitute k with k+1 in the formula to get these lines. Notice that I write out what I want to prove.

Step-2: Now start with the left side of the equation

1+2+...+(k+1)=1+2+...+k+(k+1)

=k(k+1)/2 + (k+1)

=(k(k+1)+2(k+1))/2 by 2/2=1 and distribution of division over addition

=(k+2)(k+1)/2 by distribution of multiplication over addition

=(k+1)(k+2)/2 by commutativity of multiplication

Example-3: Prove the following by using the principle of mathematical induction for all n ∈ N-

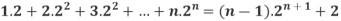
Sol. Here, n = 1, 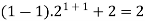, which is true

Step-1: Assume n = k holds-

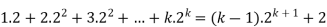
Now show n = k + 1 also holds-

Consider-

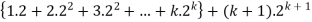
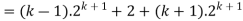
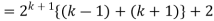
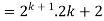
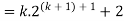
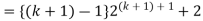
Which is also true for n = k + 1.

Hence proved.

1.4 Propositions (Propositions, logical connectives, conditional and Bi-conditional proposition)

A proposition (or statement) is a declarative statement which is true or false, but not both.

Example-

(i) Ice floats in water.

(ii) China is in Europe

(iii) 2 + 2 = 4

(iv) 2 + 2 = 5

Compound proposition-

Many propositions are composite, that is, composed of sub-propositions and various connectives discussed

Subsequently such composite propositions are called compound Propositions. A proposition is said to be primitive

if it cannot be broken down into simpler propositions, that is, if it is not composite.

Following two propositions are composite:

“Roses are red and violets are blue.” and “John is smart or he studies every night.”

Basic logical operations-

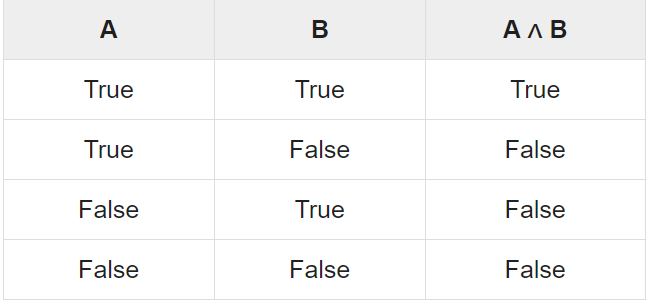
1. Conjunction- p ⋀ q

Any two propositions can be combined by the word “and” to form a compound proposition called the conjunction of the original propositions. Symbolically,

p ∧ q

Read “p and q,” denotes the conjunction of p and q. Since p ∧ q is a proposition it has a truth value, and this truth

Value depends only on the truth values of p and q.

Note- If p and q are true, then p ∧ q is true; otherwise p ∧ q is false.

2. Disjunction, p ∨ q

Any two propositions can be combined by the word “or” to form a compound proposition called the disjunction of the original propositions. Symbolically,

p ∨ q

Read “p or q,” denotes the disjunction of p and q. The truth value of p ∨ q depends only on the truth values of p

And q as follows-

If p and q are false, then p ∨ q is false; otherwise p ∨ q is true

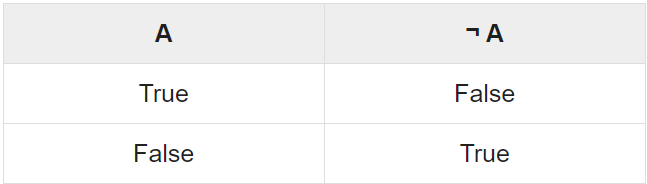
Negation-

Given any proposition p, another proposition, called the negation of p, can be formed by writing “It is not true that . . .” or “It is false that . . .” before p or, if possible, by inserting in p the word “not.” Symbolically, the negation of p, read “not p,” is denoted by

                                                         ￢p

The truth value of ￢p depends on the truth value of p as follows-

If p is true, then ￢p is false; and if p is false, then ￢p is true

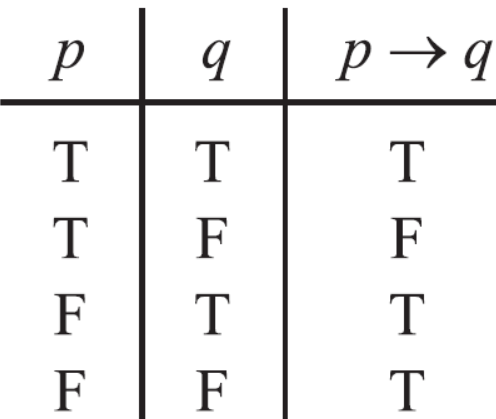
Conditional and bi-conditional statement-

The statements are of the form “if p then q”. such statements are called conditional statement and these are denoted by-

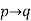
We read it as p implies q.

And another statement is of the form “p if and only if q”, such statement are called bi-conditional statement and it is denoted by-

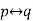
The truth value for conditional and bi-conditional value are given in the following tables-

1.5 Logical equivalences

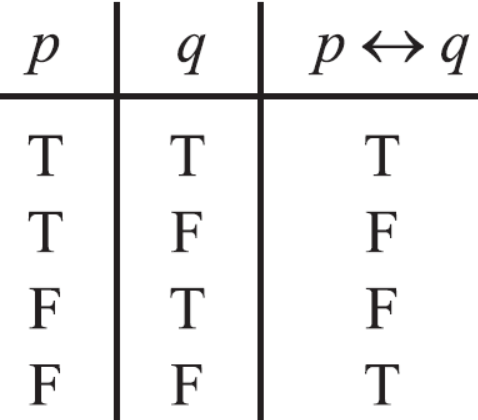
Logical equivalences-

Two propositions P (p, q, . . .) and Q(p, q, . . .) are said to be logically equivalent, or simply equivalent and denoted by

                                         P(p, q, . . .) ≡ Q(p, q, . . .)

Note- the prepositions are logically equivalent.

Prepositions and truth tables-

Supoose P(p, q, . . .) denote an expression constructed from logical variables p, q, . . ., which take on the value

T or F which are true and false, and the logical connectives ∧, ∨, and ￢ and others. Such an expression P(p, q, . . .) will be called a proposition.

The main property of a proposition P(p, q, . . .) is that its truth value depends exclusively upon the truth values of its variables, that is, the truth value of a proposition is known once the truth value of each of its variables

is known. A simple concise way to show this relationship is through a truth table

Laws of prepositions-

The prepositions satisfy the following rules

Tautologies-

A tautology is a formula which is always true for every value of its propositional variables-

Contradiction-

A Contradiction is a formula which is always false for every value of its propositional variables.

Contingency-

A Contingency is a formula which has both some true and some false values for every value of its propositional variables.

1.6 Validity of arguments by using truth tables

An argument is an assertion that is given set of prepositions 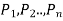called premises, yields another preposition Q, called conclusion.

Such an argument is denoted by-

The notion of a “logical argument” is defined as follows-

The argument is said to be valid if Q is true whenever all the premises 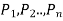are true.

Note- An argument which is not valid is called fallacy.

Example: the following argument is valid-

The proof of this rule follows from the truth table given below-

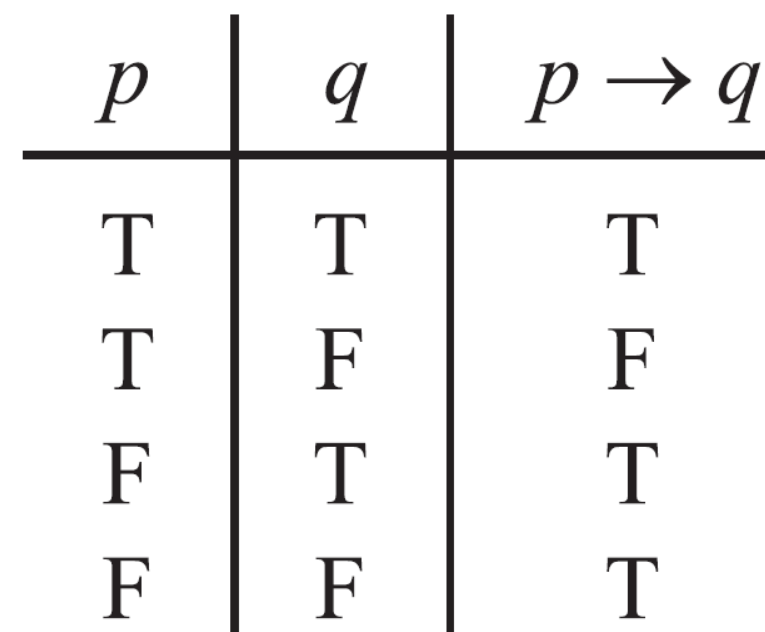
Consider an example-

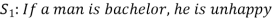
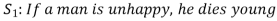
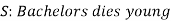
Here S denotes the conclusion of the argument and statements are the premises.

Here we claim the argument 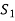, is valid

1.7 Predicates, quantifiers and normal forms

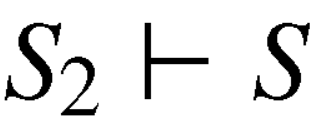
The symbols 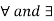are called quantifiers, here 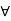is universal quantifier and 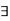is existential quantifier.

We read them as-

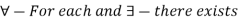
Universal quantifier-

Let p(x) is a propositional function defined on a set A, consider the expression

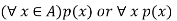
Here the symbol which we read “for all” or “for every” is called universal quantifier.

The above statement can be written as-

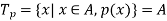
That is, that the truth set of p(x) is the entire set A.

The expression p(x) is an condition itself and it has no truth value

Example: The preposition (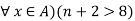 is false since {n |  n + 2 > 8} = {7, 8, …..} ≠ N

Existential quantifier-

Let p(x) be a propositional function defined on a set A. consider an expression-

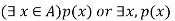
The symbol 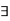reads as there exists is called existential quantifier.

De-Morgan’s theorem-

Theorem-1

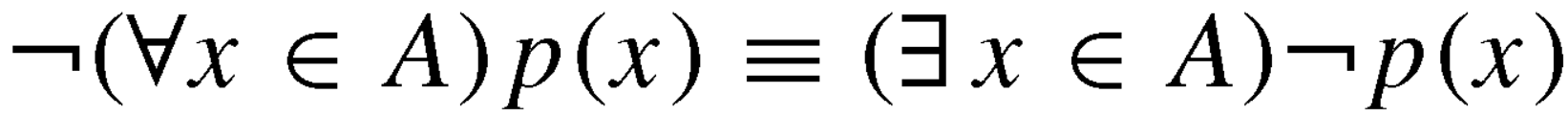
Theorem-2

Normal forms 

An atomic formula and the negation of an atomic formula are together called literals. We say that a formula A is in disjunctive normal form (DNF) if it is a disjunction of conjunctions of literals. We say that a formula A is in conjunctive normal form (CNF) if it is a conjunction of disjunctions of literals. Both DNF and CNF are called normal forms.

1.8 Application of sets and propositions

Set theory is a branch of mathematics that deals with the properties of well-defined collections of objects such as numbers and functions.

German mathematician George Cantor introduced a theory of abstract sets of entities.

Set theory is used in the following areas of computer science-

1. Data structure

2. object-oriented systems

3. Databases

4. Machine learning

Many mathematical concepts can be defined precisely using set theory concepts.

Graphs, manifolds, rings and vector spaces can all be defined as sets.

Fuzzy set theory is a sweeping statement of set theory. Fuzzy sets deals with a particular kind of uncertainty.

In axiomatic set theory, axioms are set to be describe sets.

Propositions have many applications in computer science like designing of computing machines, AI, definition of data structures for programming languages etc.

Propositional logic concerned with statements to which the truth values “true” and “false” can be assigned.

A proposition is a collection of declarative statements that has either a truth value “true” or a truth value “false”

Applications of propositional logics are-

1. System specification

2. Boolean searching

3. Logic puzzles

4. Logic circuits