UNIT-2

Combinatorics and discrete probability

2.1 Rules of sum and product, permutations and combinations

Sum rule-

Suppose S be a set and | S | denote the number of elements in S.

If S is a union of disjoint non-empty subsets

A1, A2,…,An then

|S| = |A1| + |A2| + … + |An|

In the above statement the subsets Ai of S are all disjoint i.e., they have no element in common. If Ai

And Aj an two subsets of S, then

Ai ∩ Aj = ∅ i ≠ j

And we have

S = A1 ∪ A2 ∪ A3 ∪ ... ∪ An

That is each element of S is exactly in one of the subsets Ai. In other words, the subsets A1, A2,… An is a partition of S. We now state the sum rule for counting events.

Let S be a sample space. Two events E1 and E2 of X are said to be mutually exclusive if the events have no elements in common. If E1, E2, E3, … En, are mutually exclusive events of S, then we can state

Sum rule for counting events as follows:

If E1, E2… En are mutually exclusive events of a sample space S and E1 can happen in m1 ways. E2 can happen in m2 ways…

En can happen in mn ways then E1 or E2 or … or En can happen m1 + m2 + …

+ mn ways.

Sum rule principle-

Let A and B are two disjoint sets, then-

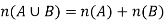
Product rule principle-

Let A × B is the Cartesian product of two sets A and B, then-

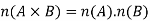
Example-1: How many ways can we draw a club or a diamond from a pack of cards?

Solution: As we know that there are 13 clubs and 13 diamonds in a pack of cards.

The number of ways a club or a diamond may be drawn 13 + 13 = 26.

Example-2: In how ways can be drawn an ace or a king from an ordinary deck of playing cards?

Solution:

Number of Aces in a pack = 4

Number of kings in a pack = 4

Number ways an Ace or a king can be drawn from the pack = 4 + 4 =

Product rule-

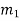If , , …, En are events, and E can happen in ways 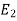can happen 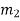ways, … 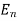can happen in 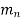ways, then the sequence of events E, first followed by 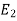followed by 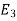, …, followed by 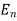can happen in m1 × m2 × … × mn ways

Example-1: In how many different ways one can answer all the questions of a true-false test consisting of 4 questions?

Solution: There are two ways of answering each of the 4 questions. Therefore by product rule the

Number of ways in which all the 4 questions can be answered-

= 2 × 2 × 2 × 2 = 16

Permutations-

A permutation of n objects taken r at a time is an arrangement of r of the objects

(r ≤ n).

The symbols of permutations of n things taken r at a time are-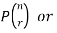

Example 1: Consider the three letters x, y, z. The arrangements of the letter x, y, z taken two at a time are-

xy, yx, xz, zx, yz, zy

∴ The number of 2-arrangements are 6 i.e., the number of permutation of 3 letters taken 2 at a time

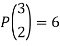
Note-A permutation of n objects taken r at a time is also called r-permutation

Factorial function-

The product of the positive integers from 1 to n is deoted by n! and we read it as “factorial “

Expressed as-

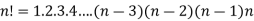
Note-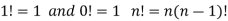

Binomial coefficient-

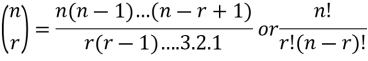
Example:

1.

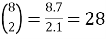
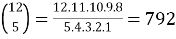
Permutation-

The arrangement of a set of n objects in a given order is called a permutation.

Any arrangement of any 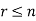of these objects in a given order is said to be r-permutation.

The number of permutations of n objects taken r will be denoted as-

P(n, r)

Formula-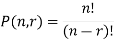 

Permutation with repetitions-

The number of permutations of n objects of which are 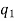are alike, 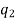are alike,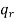

are alike is-

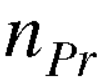
Sampling with or without replacement-

Suppose we chose the samples with repetition, fro example if we draw a ball from a urn then we put back that ball in the urn and again we pick a ball and we continue the process, so this is the case of sampling with repetition

Then the product rule tells us that the number of such samples is-

n.n.n.n.n……….n.n =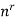

And if we pick a ball from the urn and we do not put it back to the urn, then this is the case of sampling without replacement.

So that in this case the number of samples are given as-

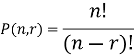
Example-

Three cards are chosen one after the other from a 52-card deck. Find the number m of ways

This can be done: (a) with replacement; (b) without replacement.

Sol.

(a) Each card can be chosen in 52 ways. Thus m = 52(52)(52) = 140 608.

(b) Here there is no replacement. Thus the first card can be chosen in 52 ways, the second in 51 ways, and the third in 50 ways. So that-

P(52, 3) = 52(51)(50) = 132 600

Example-

There are 4 black, 3 green and 5 red balls. In how many ways can they be arranged in a row?

Solution: Total number of balls = 4 black + 3 green + 5 red = 12

The black balls are alike,

The green balls are, and the red balls are alike,

The number of ways in which the balls can be arranged in a row =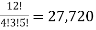

Example- A box contains 10 light bulbs. Find the number n of ordered samples of:

(a) Size 3 with replacement,

(b) Size 3 without replacement.

Solution:

(a) n =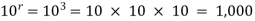

(b) P (10, 3) = 10 × 9 × 8 = 720

Circular permutations-

A circular permutation of n objects is an arrangement of the objects around a circle.

If the n objects are to be arranged round a circle we take an objects and fix it in one position.

Now the remaining (n – 1) objects can be arranged to fill the (n – 1) positions the circle in (n – 1)! ways.

Hence the number of circular permutations of n different objects = (n – 1)!

Combinations-

A combination of n objects taken at a time is an unordered selection of r of the n

Objects (r ≤ n).

A combination of n objects taken r at a time is also called r-combination of n objects.

The number of combinations is given by-

C(n, r)

Note-

1. property-1

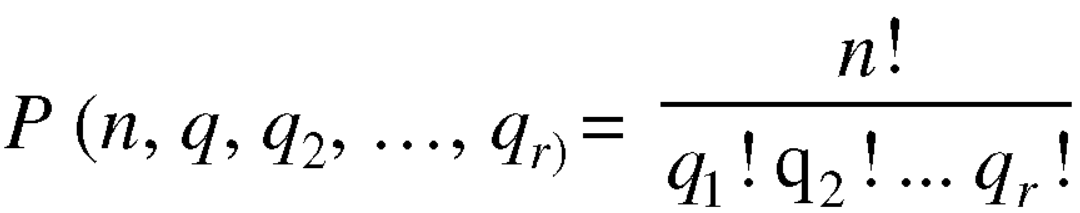
2. property-2

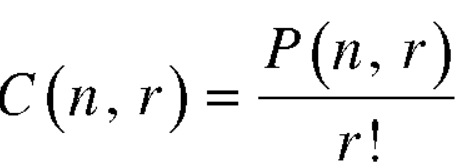
3. property-3

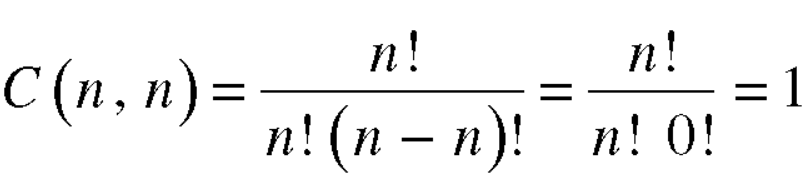
Generalized permutations and combinations

Generalized sum rule-

If we have tasks 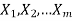that can be done in 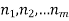ways respectively, and no two of these tasks can be done at the same time then there are 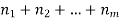ways to do one of these task.

Generalized product rule-

If we have sequential task 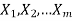that can be done in 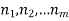, then there are 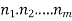to do the procedure.

Permutation and combination with unlimited repetitions-

Suppose U (n, r) denotes r-permutations of n-objects with unlimited repetitions and v (r, n) denotes the r-combination with unlimited repetitions, then-

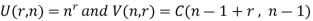
Let us consider a set 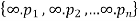where 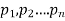are all distinct.

Any r-combination is of the form 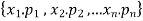here each 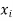is a non-negative integer and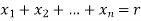

The numbers 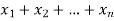are called repetition numbers. Conversely any sequence of non-negative integers-

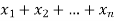
Corresponds to a r-combination .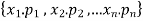

The following observation we get-

The number of r-combination of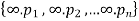

              = the number of non-negative integer solution of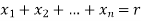

              = the number of ways of placing r indistinguishable balls in n numbered boxes.

              = the number of binary numbers with n – 1 one’s and zeros.

              = C (n – 1 + r, r)

              = C (n – 1 + r, n - 1)

Example: Find the number of non-negative integral solutions to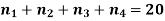

Sol: We have n = 4, r = 20

The number of non-negative integral solutions

= C (4 – 1 + 20, 20)

= C (23, 20)

= 1,771

Example-Find the number of ways of placing 8 similar balls in 5 numbered boxes.

Solution:

The number of ways of placing similar balls in 5 numbered boxes is

= C (5 – 1 + 8, 8)

= C (12, 8) = 495

Example-How many outcomes are possible by costing a 6 faced die 10 times?

Solution:

This is same as placing 10 similar balls into 6 numbered boxes.

There are C (6 – 1 + 10, 10)

= C (15, 10) possible outcomes.

2.2 Discrete probability

Introduction-

In real life situations problems are uncertain sometime. The probability theory is all about drawing inferences from uncertain problems.

Probability theory is a mathematical modelling of the phenomenon of randomness.

Sample space and event-

Suppose we are tossing a coin then there will be two outcomes head or tail.

If we roll a dice then we can get- 1, 2, 3, 4, 5, 6.

Sample space is the set of all possible outcomes of a given experiment.

An element of this sample space is called sample point.

Sample space of tossing two coins-

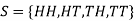
And sample point is {HH} or {TT} or {HT} etc.

Event- An event in a sample space S is a collection of sample points.

Mutually exclusive events-

Two events are said to be mutually exclusive if they can not occur at the same time.

Probability-

Let S be a sample space, and each outcome of an experiment is equally likely and the number of outcomes is finite.

If A is an event connected with the experiment, then the probability of occurrence of event A is given by-

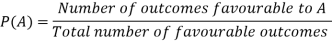
 Example: If a card is selected from the pack of playing cards then what will be the probability of the following cases?

1. A = {the card is a diamond}

2. B = {the card is a face card}

Sol.

As we know that-

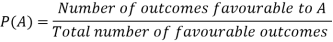
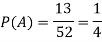
And \

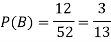
Note-

1. The probability of an event lies between 0 to 1, i.e.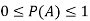

2. If events A and B are mutually exclusive then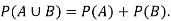

3. Let A be any event then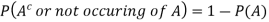

4. The sum of all probabilities in the sample space is 1.

5. The probability of an event which can not occur is 0.

Addition rule of probability-

For any events A and B,

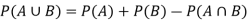
Example: In a college counselling, 30 students are choosing maths, 20 are choosing Computer science and 10 are selecting maths and computer science.

Suppose a student is selected randomly from 100 students then find the probability that student choose maths or computer science.

Sol.

Let A = {student is taking maths} and B = {student taking computer science}

So that the probabilities will be-

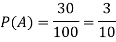
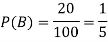
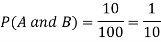
Hence by the addition principle of probability-

2.3 Conditional probability

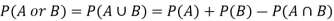
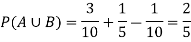
Let A and B are two event in a sample space S and P(B)≠0. then the probability that an event A occurs once B has occurred or the conditional probability of A given B which is defined as-

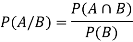
Note- If two events A and B are independent then-

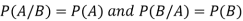
Multiplication theorem for conditional probability-

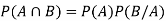
Example: A bag contains 12 pens of which 4 are defective. Three pens are picked at random from the bag one after the other.

Then find the probability that all three are non-defective.

Sol. here the probability of the first which will be non-defective = 8/12

By the multiplication theorem of probability,

If we draw pens one after the other then the required probability will be-

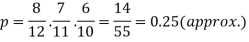
Example: The probability of A hits the target is 1 / 4 and the probability that B hits the target is 2/ 5. If both shoot the target then find the probability that at least one of them hits the target.

Sol.

Here it is given that-

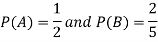
Now we have to find-

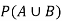
Both two events are independent. So that-

2.4 Bayes theorem

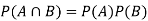
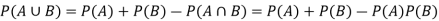
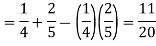
Let 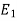and 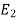be mutually exclusive events forming a portion of the sample space S and let E be any event of the sample space such that P(E) ≠ 0.

Then-

The Bayes theorem can be defined as-

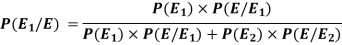
Example: An urn I contains 3 white and 4 red balls and an urn II contains 5 white and6 red balls. one ball is drawn at random from one of the urns and is found to be white.

Find the probability that it was drawn from urn I.

Sol. Let

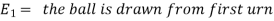
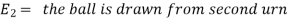
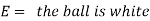
Now we have to find-

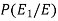
So that by using Bayes theorem, we get-

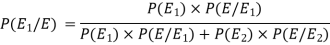
Here,

Two urns are equally likely to select,

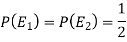
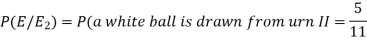
So that-

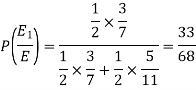
Example: In a bolt factory, machines A, B and C manufacture respectively 25%, 35% and 40% of the total. If their output 5, 4 and 2 per cent are defective bolts. A bolt is drawn at random from the product and is found to be defective. What is the probability that it was manufactured by machine B?

Sol. here-

A: bolt is manufactured by machine A

B: bolt is manufactured by machine B

C: bolt is manufactured by machine C

So that- P(A) = 0.25, P(B) = 0.35 and P(C) = 0.40

The probability of drawing a defective bolt manufactured by machine A is P(D/A) = 0.05

P (D/B) = 0.04 and P (D/C) = 0.02

Therefore by using Bayes theorem-

2.5 Information and mutual information

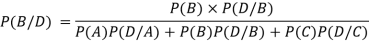
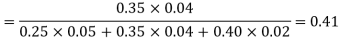
Information is a mathematical approach to the study of coding of information along with the quantification, storage, and communication of information.

The mutual information of two random variables is a quantity that measures the mutual dependence of the two variables. Intuitively, the mutual information "I(X : Y)" measures the information about X that is shared by Y.

If X and Y are independent, then X contains no information about Y and vice versa, so their mutual information is zero. If X and Y are identical then all information conveyed by X is shared with Y: knowing X reveals nothing new about Y and vice versa, therefore the mutual information is the same as the information conveyed by X (or Y) alone, namely the entropy of X. In a specific sense (see below), mutual information quantifies the distance between the joint distribution of X and Y and the product of their marginal distributions.

If we consider pairs of discrete random variables (X, Y), then formally, the mutual information can be defined as: I(X : Y) :  = H(X) + H(Y) − H(XY) with H(X), H(Y) the Shannon entropy of "X" and "Y", and H(XY) the Shannon entropy of the pair "(X,Y)". In terms of the probabilities, the mutual information can be written as-

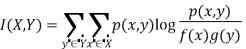
Here p is the joint probability distribution of X and Y and f, g are the marginal probability distribution functions of X and Y.

For continuous case, we replace the summation by definite double integration.

2.6 Application of combinatorics and discrete probability

Combinatorics is an important part of discrete mathematics. This is the study of arrangement of objects.

Combinatorics has many applications in various field of mathematics such as-

1. Computer architecture

2. Scientific discovery

3. Languages

4. Cryptography

5. Pattern analysis

6. Simulation

7. Data base and data mining

8. Operations research

Combinatorics helps us to count the numbers.

Suppose we have 4 seats and we want to 4 students to sit on them. So that there are 4 students who could sit on the first seat. Then there are 3 students who could sit on the second seat, there are two options for the third seat and one option for the last seat.

So that total possibilities-

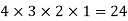
We get that there are n! possibilities to order n objects.

Permutation in combinatorics are related to rearranging the values or objects.

Example: Suppose we want to know how many words we can make by using 3 letters from the word DELHI.

So in this case we can find it by using permutations-

Therefore by permutation-

The required number of words- by using the formula of permutation-

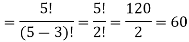
So that we can make 60 words by using 3 words of the word DELHI.

Example: If there is team of 15 players, so that in how many ways we can select a team of 4 players.

Sol.

Here the number of possible ways of selection-

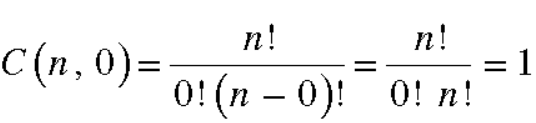
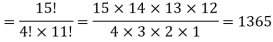
Applications of discrete probability-

Probability theory is a fundamental tool of many disciplines of science and engineering.

Discrete probability is basically concerned with drawing conclusions from experiments involving uncertainties.

A probabilistic mathematical model of random phenomena is defined by assigning “probabilities” to all the possible outcomes of an experiment. The reliability of our mathematical model for a given experiment depends upon the closeness of the assigned probabilities to the actual limiting relative frequencies. This then gives rise to problems of testing and reliability, which form the subject matter of statistics and which lie beyond the scope of this text.