UNIT-3
Graph theory
Basic terminology-
Graph theory is a relatively new area of mathematics
Graph is the form of representing of descriptive data in the terms of verticals and edges.
Graph theory is used in various fields like computer science, information technology, genetics, telecommunication etc.
A graph is a collection of vertices and edges in which each edge is assigned to pair of points called terminal.
We can say that a graph is a network of dots connected by lines.
Mathematically we can define a graph as-
A graph is a pair of set (V, E) where-
1. V is a non-empty set whose elements are called vertices.
2. E is collection of two-element subset of V called edges.
Terminology: A graph G is an ordered pair (V, E) where V is a non-empty set and E is the set of edges in which each element of E is assigned to a unique unordered pair of elements of V.
An element of a set E is generally denoted as- e = (v,u) where u, v ∈ V.
U and v are called the end vertices of edge e.
Note- In any graph the number of vertices with odd degree must be even.
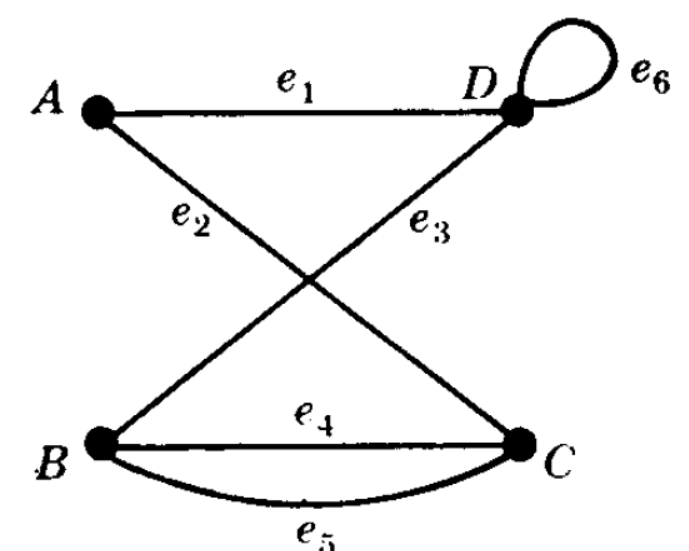
Loop: If both the end vertices of an edge are same then the edge is called a loop.
Parallel edge: If two or more edges have same terminal vertices, then these edges are called parallel edges.
Example: Consider the graphs given below-
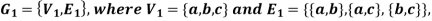
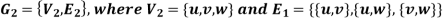
Check whether these graphs are same or not?
Sol.
As we can see that these graphs are not same because here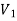 
and 
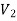are not same since 
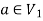but a does not belongs to 
.
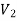These two graphs look same but not equal.
We can draw these graphs as below-
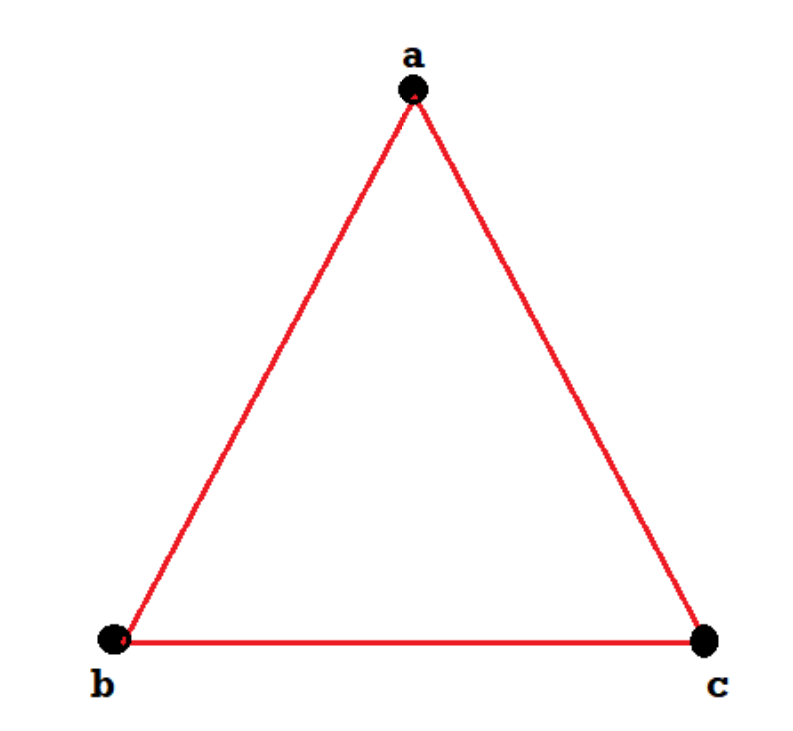
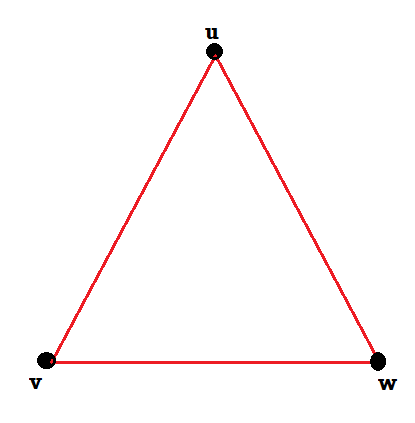
These types of graphs are known as isomorphic graph when they are same except for the name of vertices.
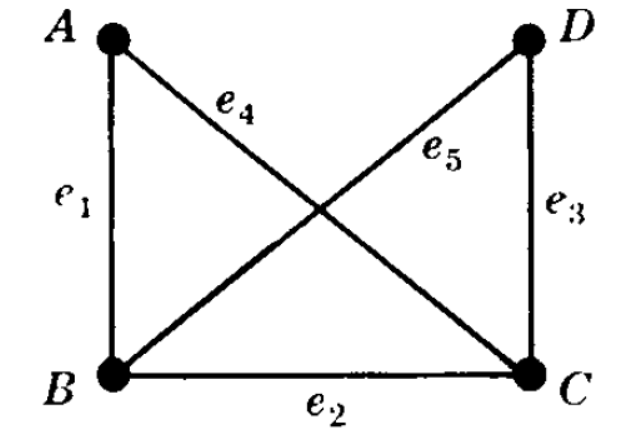
Simple graph: A graph which has no loops and parallel edges is known as simple graph.
Compound graph: A graph which contains loops or parallel edges is called compound or multi-graph.
Degree of vertex: The number of edges incident on a vertex v is called degree of vertex v, with loop being counted twice.
We can denote it as-
Degree of v = d(v)
Examples of graph and multi-graph are-
Graph-
Multi-graph-
Weighted Graphs
A graph G is said to be a weighted graph if each edge e of G is assigned a non-negative number w(e) called the weight of v.
The weighted graph is given below-
Sub Graphs-
We can say that 
is a sub-graph of G = (V, E), and write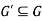 
provided 
.
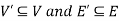We can say that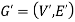 
is an induced sub-graph of G = (V, E), provided 
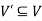and every edge in E whose vertices are still in 
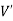is also an edge in 
.
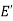Isomorphic graphs-
Let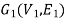 
and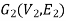 
be two graphs. The graph 
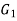and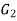 
are said to be isomorphic if there is a bijective function 
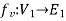such that if u and v are end vertices of some edge e ∈ 
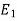then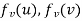 
end vertices of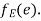 
Complete Graphs-
A simple graph G is called a complete graph, if there is an edge between each pair of vertices.
Regular Graphs-
If all vertices of a graph G have same degree, then G is called as a regular graph.
Bipartite Graphs-
A graph G(V, E) is said to be bipartite, if the vertex set V can be partitioned in to two non-empty disjoint subset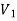 
and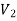 
such that each edge is G had end vertex is 
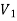and other end vertex in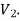 
There is no edge between two vertices of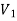 
as well as there is no edge between two vertices of 
.
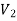Here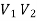 
bipartition of V.
Following are basic operations of a Graph −
Add Vertex − Adds a vertex to the graph.
Add Edge − Adds an edge between the two vertices of the graph.
Display Vertex − Displays a vertex of the graph.
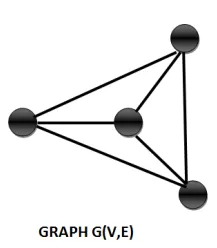
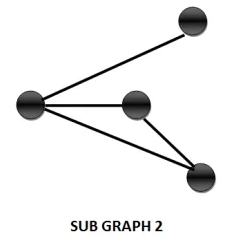
Sub graph
Getting a sub graph out of a graph is an interesting operation. A sub graph of a graph G(V,E) can be obtained by the following means:
1. Removing one or more vertices from the vertex set.
2. Removing one or more edges from the edge family.
3. Removing either vertices or edges from the graph.
4. The vertices of sub graphs are subsets of the original vertices
5. The edges of sub graphs are subsets of the original edges
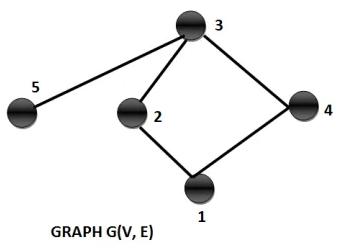
Neighbourhood graph
The neighbourhood graph of a graph G(V,E) only makes sense when we mention it with respect to a given vertex set. For e.g. if V = {1,2,3,4,5} then we can find out the Neighbourhood graph of G(V,E) for vertex set {1}.
So, the neighbourhood graphs contains the vertices 1 and all the edges incident on them and vertices connected to these edges.
Example:
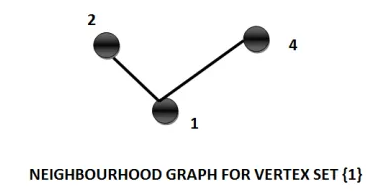
Example:
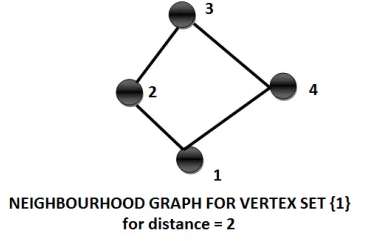
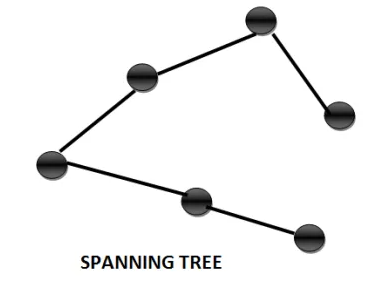
Spanning Tree
A spanning tree of a connected graph G(V,E) is a sub graph that is also a tree and connects all vertices in V. For a disconnected graph the spanning tree would be the spanning tree of each component respectively.
There is an interesting set of problems related to finding the minimum spanning tree (which we will be discussing in upcoming posts). There are many algorithms available to solve this problem, for e.g.: Kruskal’s, Prim’s etc. Note that the concept of minimum spanning tree mostly makes sense in case of weighted graphs. If the graph is not weighted, we consider all the weights to be one and any spanning tree becomes the minimum spanning tree.
We can use traversals like Breadth First Scan and Depth First Scan to fight the Spanning Tree. We can find spanning tree for undirected graphs, directed graphs, multi graphs as well.
Example:
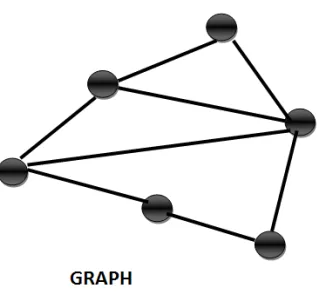
Conversion from Directed Graph to Undirected graph
This is the simplest conversions possible. A directed graph has directions represented by arrows, in this conversion we just remove all the arrows and do not store the direction information.
Example:
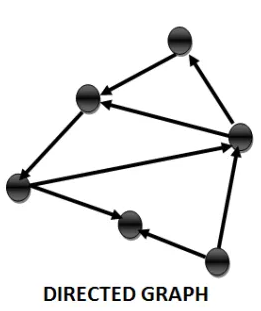
Conversion from Undirected Graph to Directed graph
This conversion gives a directed graph given an undirected graph G(V,E). It is the exact reverse of the above. The trick to achieve this is to add one edge for each existing edge in the edge family E. Once the extra edges are added, we just assign opposite direction to each pair of edges between connecting vertices.
Example:
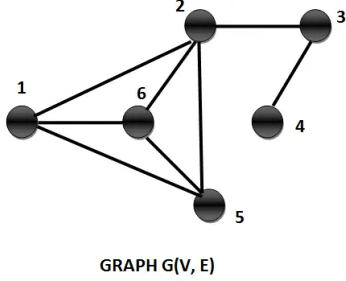
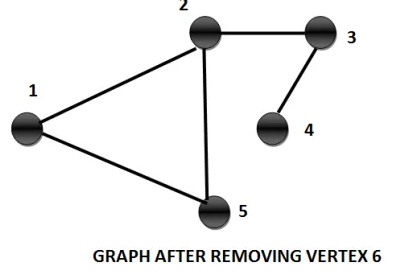
Delete Vertex
What happens when we delete a vertex from a given Graph G(V, E)?
We cannot successfully remove a vertex if we do not remove all the edges incident on the vertex. Once we remove the vertex then the adjacency matrix will not contain the row and column for the corresponding vertex.
This operation changes the vertex set and the edge family of the graph.
Example:
Path-
A path is a walk that does not repeat any vertices (or edges) except perhaps the first and last. If a path starts and ends at the same vertex, it is called a cycle.
Circuit-
A Hamiltonian circuit is a closed walk in a graph which visits each vertex exactly once. The start and end vertex (which happens to be the same) is visited twice.
In a Hamiltonian Circuit of N vertices, there would be exactly N edges. Since a Hamiltonian Circuit cannot visit the same vertex twice, hence there cannot be any loops or parallel edges. Thus all such circuits are simple graphs. And to connect each of the N vertex we need N-1 edges, to connect the first and the last vertex and close the walk, we need one more edge. Hence, N vertex Hamiltonian circuit will have exactly N edges.
If you remember from our last post, we proved that the necessary and sufficient condition for Euler Lines is that each vertex must have even degree. On the same lines if we try to establish a necessary and sufficient condition for existence of Hamiltonian Circuit in a graph we will miserably fail.
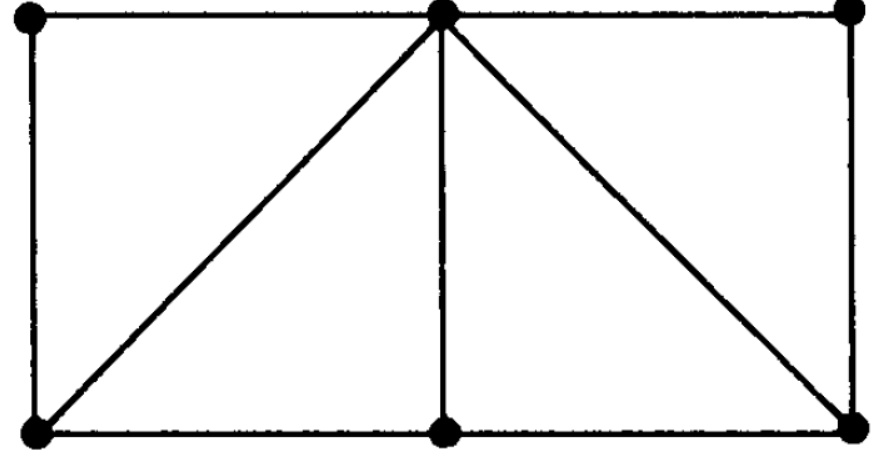
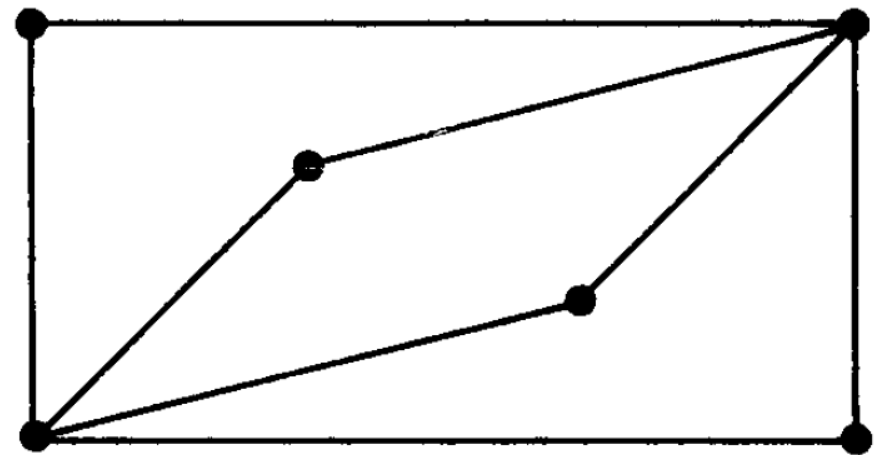
Hamiltonian and Euclerian graphs-
Eulerian graph- A graph G is called an Eulerian grap
h if there exists a closed transversal trail, called an Eulerian trail.
Hamiltonian graph- A closed path that visits every vertex in G exactly once and if G admit a Hamiltonian circuit, then G is called Hamiltonian graph.
Note- An Eulerian circuit traverses every edge exactly once, but many repeats vertices.
While a Hamiltonian circuit visits each vertex exactly once but many repeats edges.
Following are the examples of Hamiltonian and Eulerian graph respectively-
Travelling Salesman Problem-
The “Traveling-salesman” problem refer to finding a Hamiltonian circuit for G of minimum weight.
Theorem-The complete graph Kn with n ≥ 3 vertices has H = (n − 1)!/2 Hamiltonian circuits (where we do not distinguish between a circuit and its reverse).
Consider the complete weighted graph G in Fig. 8-35(a). It has four vertices, A, B, C, D. By Theorem 8.13 it has H = 3!/2 = 3 Hamiltonian circuits. Assuming the circuits begin at the vertex A, the following are the three circuits and their weights:
|ABCDA| = 3 + 5 + 6 + 7 = 21
|ACDBA| = 2 + 6 + 9 + 3 = 20
|ACBDA| = 2 + 5 + 9 + 7 = 23
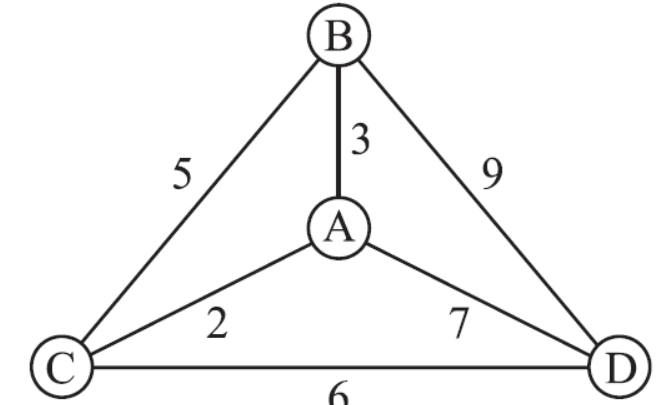
Thus ACDBA with weight 20 is the Hamiltonian circuit of minimum weight.
Planar graph-
When a connected graph can be drawn without any edges crossing, it is called planar.
When a planar graph is drawn in this way it divides the plane into region called faces.
The following graph is a planar graph-
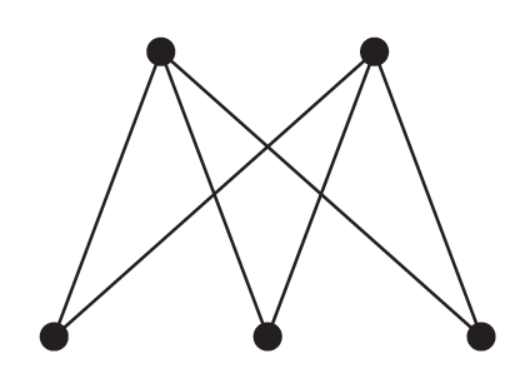
We can draw it like this-
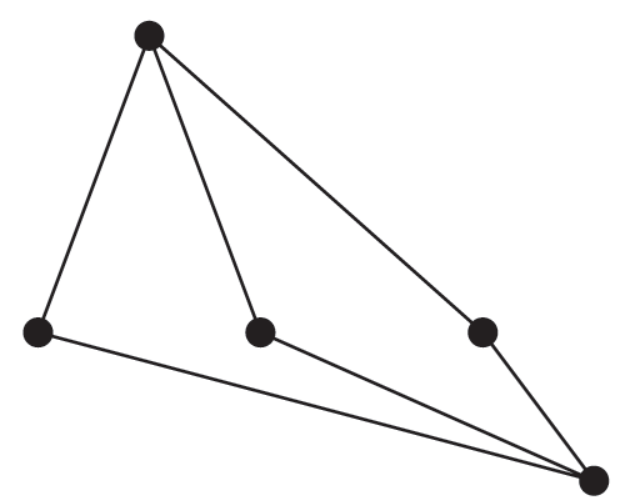
Euler’s formula for planar graph-
For any planar graph with v vertices, e edges and f faces, we have-
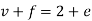
Graph colouring-
A coloring of G is an assignment of colors to the vertices of G such that adjacent vertices have different colors. We say that G is n-colorable if there exists a coloring of G which uses n colors.
The minimum number of colors needed to paint G is called the chromatic number of G and is denoted by χ(G).
Trees-
A graph T is called a tree if T is connected and T has no cycles.
A graph without cycle is said to be a cycle-free.
The tree consisting of a single vertex with no edges is called the degenerated tree.
One thing to keep in mind is that while the trees we study in graph theory are related to trees you might see in other subjects, the correspondence is not exact. For instance, in anthropology, you might study family trees, like the one below
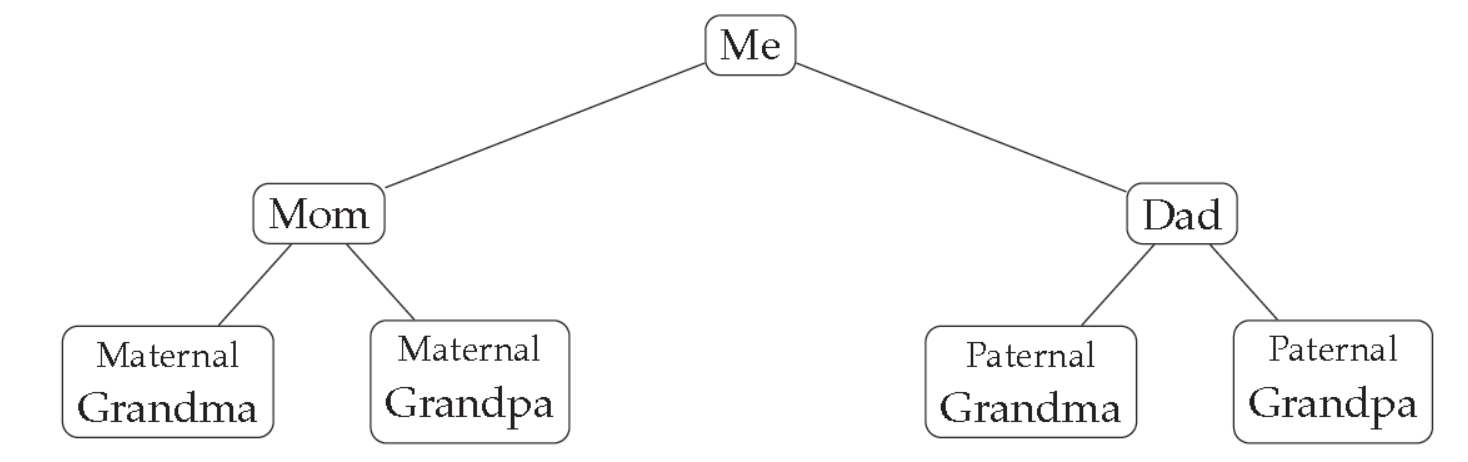
So far so good, but while your grandparents are (probably) not blood relatives, if we go back far enough, it is likely that they did have some common ancestor. If you trace the tree back from you to that common ancestor, then down through your other grandparent, you would have a cycle, and thus the graph would not be a tree.
You might also have seen something called a decision tree (such as the algorithm for deciding whether a series converges or diverges). Sometimes these too contain cycles, as the decision for one node might lead you back to a previous step.
Both the examples of trees above also have another feature worth mentioning: there is a clear order to the vertices in the tree. In general, there is no reason for a tree to have this added structure, although we can impose such a structure by considering rooted trees, where we simply designate one vertex as the root.
Spanning trees-
A sub-graph T of a connected graph G is called spanning tree of G if T is a tree and T includes all the vertices of G.
Rooted trees-
As soon as one vertex of a tree is designated as the root, then every other vertex on the tree can be characterized by its position relative to the root. This works because there is a unique path between any two vertices in a tree. So from any vertex, we can travel back to the root in exactly one way. This also allows us to describe how distinct vertices in a rooted tree are related.
If two vertices are adjacent, then we say one of them is the parent of the other, which is called the child of the parent. Of the two, the parent is the vertex that is closer to the root. Thus the root of a tree is a parent, but is not the child of any vertex (and is unique in this respect: all non-root vertices have exactly one parent).
Not surprisingly, the child of a child of a vertex is called the grandchild of the vertex (and it is the grandparent). More in general, we say that a vertex v is a descendent of a vertex u provided u is a vertex on the path from v to the root. Then we would call u an ancestor of v.
For most trees (in fact, all except paths with one end the root), there will be pairs of vertices neither of which is a descendant of the other. We might call these cousins or siblings. In fact, vertices u and v are called siblings provided they have the same parent. Note that siblings are never adjacent
Example- consider the tree below-
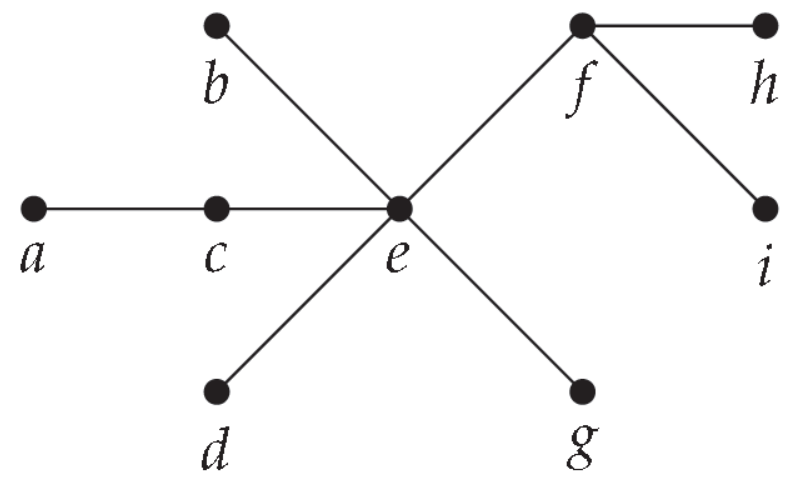
If we designate vertex f as the root, then e, h, and i are the children of f, and are siblings of each other. Among the other things we can say are that a is a child of c, and a descendant of f. The vertex g is a descendant of f , in fact, is a grandchild of f . Vertices g and d are siblings, since they have the common parent e.
Notice how this changes if we pick a different vertex for the root. If a is the root, then its lone child is c, which also has only one child, namely e. We would then have f the child of e (instead of the other way around), and f is the descendant of a, instead of the ancestor. f and g are now siblings.
Example-
Explain why every tree is a bipartite graph.
Solution.
To show that a graph is bipartite, we must divide the vertices into two sets A and B so that no two vertices in the same set are adjacent. Here is an algorithm that does just this.
Designate any vertex as the root. Put this vertex in set A. Now put all of the children of the root in set B. None of these children are adjacent (they are siblings), so we are good so far. Now put into A every child of every vertex in B (i.e., every grandchild of the root). Keep going until all vertices have been assigned one of the sets, alternating between A and B every “generation.” That is, a vertex is in set B if and only if it is the child of a vertex in set A.
Spanning trees-
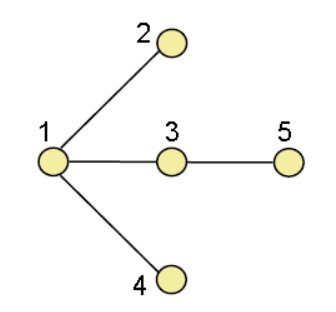
Given a connected graph G, a spanning tree of G is a sub-graph of G which is a tree and includes all the vertices of G.
Every connected graph has a spanning tree.
Example: Find two different spanning tree of the graph.
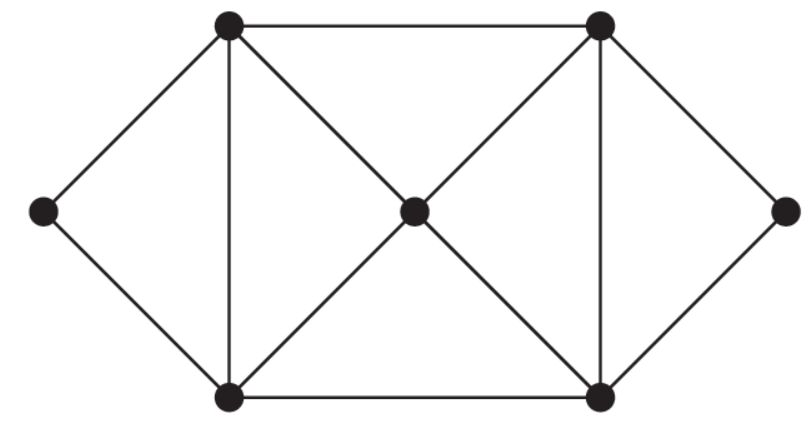
Sol-
Two spanning trees are-
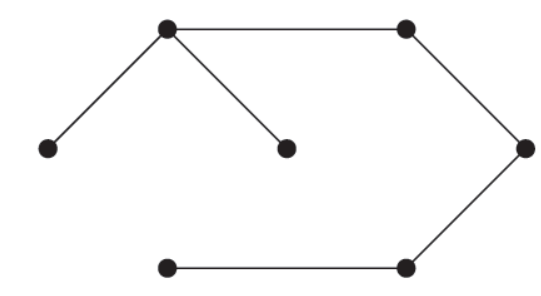
And
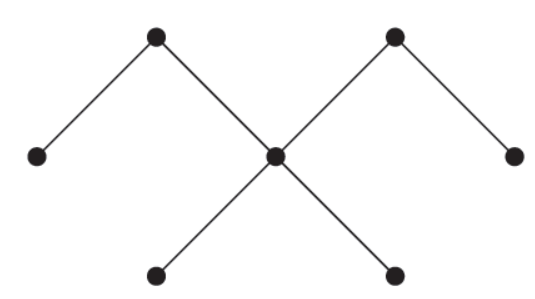
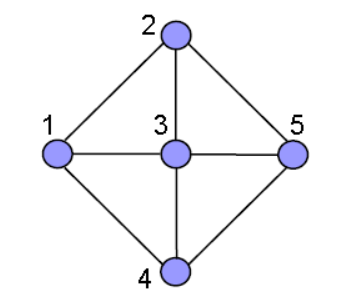
Fundamental Cut Sets-
1. A cut-set of a connected graph, is a set of edges whose removal would disconnect the graph.
2. No proper subset of a cut-set will cause disconnection.
A cut-set is denoted by the partition of vertices that it induces-
[P,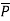 
], where
P is the subset of vertices in one component,
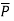= V – P
1. Let T be a spanning tree of a connected graph.
2. Any edge of T defines a partition of vertices of G:
3. The removal of this edge disconnects T
Then:
There is a corresponding cut-set of G producing the same partition.
4. This partition contains:
a. One edge of T, and
b. A number of chords of T.
Such a cut-set is called a fundamental cut-set.
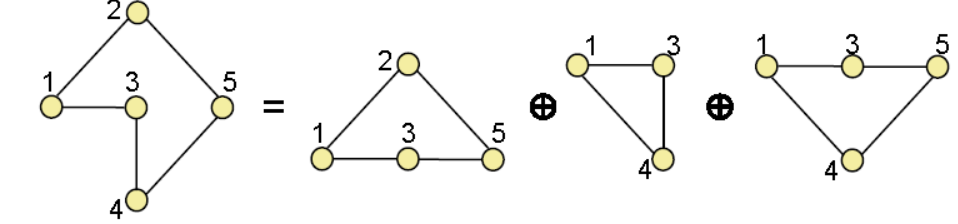
Fundamental Circuits-
1. The addition of a chord to a spanning tree creates precisely one circuit.
2. The collection of these circuits w.r.t. a particular spanning tree is a set of fundamental circuits.
3. Any arbitrary circuit of the graph may be expressed as a linear combination of the fundamental circuits using the operation ringsum.
Examples:
Circuit of G expressed with fundamental circuits-
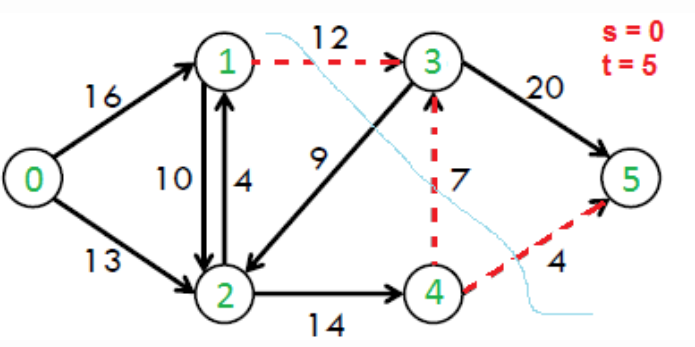
Max flow –Min Cut Theorem (Transport Network)-
n a flow network, an s-t cut is a cut that requires the source ‘s’ and the sink ‘t’ to be in different subsets, and it consists of edges going from the source’s side to the sink’s side. The capacity of an s-t cut is defined by the sum of the capacity of each edge in the cut-set.
The problem discussed here is to find minimum capacity s-t cut of the given network. Expected output is all edges of the minimum cut.
For example, in the following flow network, example s-t cuts are {{0 ,1}, {0, 2}}, {{0, 2}, {1, 2}, {1, 3}}, etc. The minimum s-t cut is {{1, 3}, {4, 3}, {4 5}} which has capacity as 12+7+4 = 23.
Graph Theory is used in modelling and solving a lot of real world problems, games and puzzles. Here we discuss a very famous puzzle ” The Instant Insanity ” problem.
The goal of this post is to demonstrate that such complicated problem statements can be so easily modeled and solved using Graph Theory. Also I would like to build some more interest into Graph Theory.
The history of graph theory may be specifically traced to 1735, when the Swiss mathematician Euler solved the Konigsberg bridge problem.
The Konigsberg bridge problem was an old puzzle concerning the possibility of finding a path over every one of seven bridges that span a forked river flowing past an island—but without crossing any bridge twice. Euler argued that no such path exists. His proof involved only references to the physical arrangement of the bridges, but essentially he proved the first theorem in graph theory.
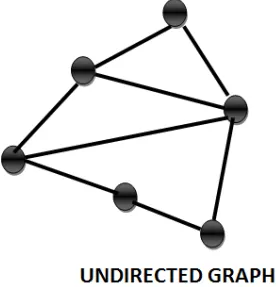
As used in graph theory, the term graph does not refer to data charts, such as line graph or bar graphs. Instead, it refers to a set of vertices (that is, points or nodes) and of edges (or lines) that connect the vertices. When any two vertices are joined by more than one edge, the graph is called a multi-graph. A graph without loops and with at most one edge between any two vertices is called a simple graph.
graph is assumed to refer to a simple graph. When each vertex is connected by an edge to every other vertex, the graph is called a complete graph. When appropriate, a direction may be assigned to each edge to produce what is known as a directed graph, or digraph.
