UNIT-4
RELATIONS AND FUNCTIONS.
4.1.1 Properties of binary relations.
Relation: The word relation suggests some familiar example relations such as the relation of father to son, mother to son, brother to sister etc. Familiar examples in arithmetic are relation such as "greater than", "less than", or that of equality between the two real numbers.
Here, we shall only consider relation called binary relation, between the pairs of objects. Before we give a set-theoretic definition of a relation we note that a relation between two objects can be defined by listing the two objects an ordered pair.
Definition: Any set of ordered pairs defines a binary relation. We shall call a binary relation simply a relation. It is sometimes convenient to express the fact that particular ordered pair say (x, y) E R where, R is a relation by writing
x R y which may be read as "x is a relation R to y".
There are some properties of the binary relation:
The relation =< is reflexive in the set of real number since for nay x we have x<= X similarly the relation of inclusion is reflexive in the family of all subsets of a universal set.
The relation <= and < are not symmetric i the set of real number while the relation of equality is.
The relation <= < and = are transitive in the set of real numbers. The relations and equality are also transitive in the family of a subset of a universal set.
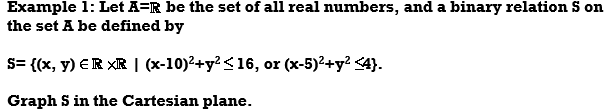
Solution: Recall from analytic geometry that a Cartesian plane is a plane with the normal x and y axis, and a circle of radius r centred at the coordinates (a,b) is given precisely by the equation
(x-a)2 +(y-b)2= r2.
Hence the equation
(x-10)2+y2=16 (=42),
represents a circle of radius 4 centred at the coordinates (10,0), and
(x-5)2+y2=4 is a circle of radius 2 centred at the coordinates (5,0).
Thus, S is the union of these 2 disks, and is represented by the shaded area in the graph below.
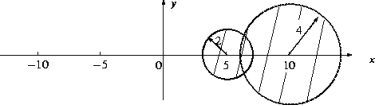
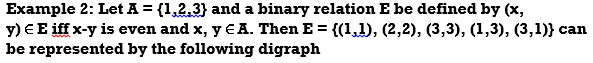
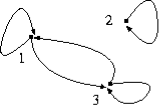
Solution:
(2,2): 2-2=0 is even, hence the loop at vertex labelled by 2  A.
A.
(1,3): 1-3=-2 is even, hence the arrow from vertex 1 to vertex 3.
4.1.2 Closure of relations.
Closure of Relations:
Reflexive closure: The reflexive closure of a relation R on A is obtained by adding (a, a) to R for each a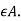
Symmetric Closure: The symmetric closure of R is obtained (b, a) to R for each (a, b) 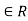
Transitive Closure: The transitive closure of R is obtained by repeatedly adding (a, c) to R for each (a, b)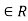 and (b,c)
and (b,c)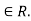
Example: Let R be relation on a set A. There is a path of length n, where n is a positive integer, from a to b if and only if (a, b)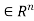
Connectivity Relation A.K.A Transitive Closures: Let R be a relation on a set A. The connectivity relation R* consists of the pairs (a, b) such that there is a path of length at least one from a to b in R.
In other words:
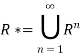
Where 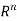 consists of the pairs (a, b) such that there is a path of length n from a to b
consists of the pairs (a, b) such that there is a path of length n from a to b
Wars hall’s Algorithm:
W = MR
for k= 1 to n do
for i = 1 to n do
for j = 1 to n do
wij = wij 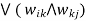
end for
end for
end for
return W {W = 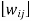 is the zero-one matrix for R*}
is the zero-one matrix for R*}
Warhsall’s algorithm is a faster way to compute transitive closure. Runs in O (n3) bit operations.
Example1: Use algorithm 1 to find the transitive closure of these relations on {1,2,3,4}.
a): {(1,2), (2,1), (2,3), (3,4), (4,1)}
Transitive Closure
= 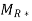
=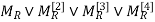

b). {(2,1), (2,3), (3,1), (3,4), (4,1), (4,3)}
Transitive Closure
= 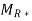
=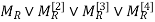

Example 2: Use Warhsall’s algorithm to find the transitive closure of these relations on {1,2,3,4}
a). {(1,2), (2,1), (2,3), (3,4), (4,1)}
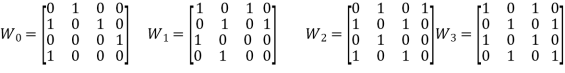
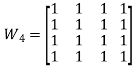
b). {(2,1), (2,3), (3,1), (3,4), (4,1), (4,3)}
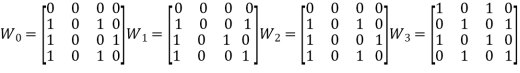
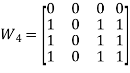
4.1.3 Equivalence relations.
Definition:
Equivalence Relation: A relation on a set A is an equivalence relation if it is reflexive, symmetric, and transitive. we often use the tilde notation 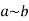 to denote a relation.
to denote a relation.
Also, when we specify just one set, such as 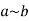 is a relation on set B, that means the domain & codomain are both set B.
is a relation on set B, that means the domain & codomain are both set B.
For an equivalence relation, due to transitivity and symmetry, all the elements related to a fixed element must be related to each other. Thus, if we know one element in the group, we essentially know all its “relatives”.
Example 1:
Theorem: If R is an equivalence relation on any non-empty set A, then the distinct set of equivalence classes of R forms a partition of A.
Proof: Suppose R is an equivalence relation on any non-empty set A. Denote the equivalence classes 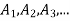
WMST 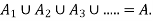
First, we will show 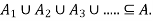
If x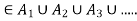 then x belongs to at least one equivalence class,
then x belongs to at least one equivalence class, 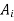 by definition of union.
by definition of union.
By the definition of equivalence class, x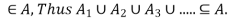
Next, we show 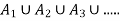
If x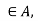 then xRx since R is reflexive. Thus x
then xRx since R is reflexive. Thus x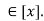
[x]=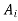 , for some I since [x] is an equivalence class of R.
, for some I since [x] is an equivalence class of R.
So,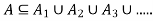 by definition of subset, And so,
by definition of subset, And so, 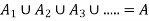 ,
,
by the definition of equality of sets.
Now WMST {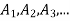 } is pairwise disjoints.
} is pairwise disjoints.
For any i,j, either 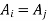 or
or 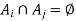 by lemma So,
by lemma So, 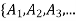 } is mutually disjoint by definition of mutually disjoint.
} is mutually disjoint by definition of mutually disjoint.
We have demonstrated both conditions for a collection of sets to be a partition and we can conclude if R is an equivalence relation on any non-empty set A, then the distinct set of equivalence classes of R forms a partition of A.
Example 2:
Theorem: If A is a set with partition P = 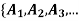 }and R is a relation induced by partition P, then R is an equivalence relation.
}and R is a relation induced by partition P, then R is an equivalence relation.
Proof: Let A be a set with partition P = 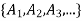 and R be a relation induced by partition P. WMST R is an equivalence relation.
and R be a relation induced by partition P. WMST R is an equivalence relation.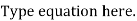
Reflexive
Let 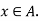 Since the union of the sets in the partition P=A, x must belong to at least one set in P.
Since the union of the sets in the partition P=A, x must belong to at least one set in P.
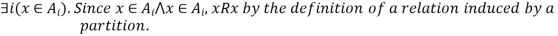
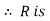 Reflexive
Reflexive
Symmetric
Suppose xRy. 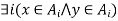 by the definition of a relation induced by a partition.
by the definition of a relation induced by a partition.
Since 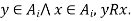
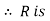 symmetric.
symmetric.
Transitive
Suppose xRy 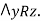
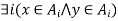 and
and 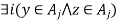 by the definition of a relation induced by a partition.
by the definition of a relation induced by a partition.
Because the sets in a partition are pairwise disjoint, either 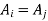 or
or 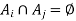 .
.
Since y belongs to both these sets, 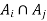
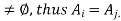
Both x and z belong to the same set, so xRz by the definition of a relation induced by a partition.
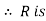 transitive.
transitive.
We have shown R is reflexive, symmetric and transitive , so R is an equivalence relation on set A.
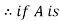 a set with partition P =
a set with partition P = 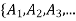 } and R is a relation induced by partition P, then R is an equivalence relation….
} and R is a relation induced by partition P, then R is an equivalence relation….
4.1.4 Partitions and partial order relations.
Partial Ordering Relations: A relation R on a set S is called a partial ordering relation, or simply a partial order, if the following 3 properties hold for this relation.
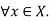
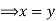
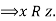
Examples:
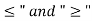
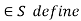
A R B if A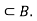 R is reflexive (A
R is reflexive (A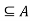 ),
),
Anti-symmetric 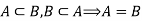
And transitive 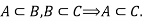
Thus, R is a partial order.
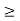
- It is reflexive: a 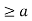 for all a
for all a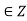
- It is anti-symmetric: if a 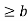 then the only way that
then the only way that 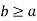 is when b=a
is when b=a
- It is transitive: if 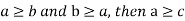
Set Partitioning:
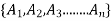
4.1.5 Lattices.
Definition: An algebraic structure (L, 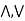 ) is said to be a lattice if it satisfies the following properties.
) is said to be a lattice if it satisfies the following properties.
Associative property: 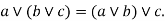
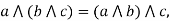
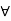 a, b
a, b 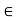 L.
L.
Commutative property: a 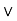 b = b
b = b 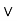 a
a
a 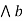 = b
= b 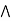 a.
a.
Absorption property: a 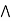 (a
(a 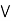 b) = a
b) = a
a 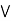 ( a
( a 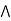 b) = a.
b) = a. 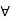 a, b
a, b 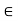 L.
L.
Idempotent property: a 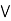 a = a
a = a
a  a= a.
a= a.  a, b
a, b  L.
L.
Example 1: a lattice L is modular 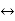 a
a 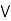 [ b
[ b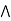 (
(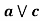 )] = ( a
)] = ( a 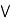 b)
b) 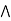 (a
(a 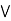 c),
c), 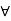 a, b,c
a, b,c 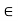 L., a
L., a 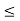 c.
c.
solution: suppose L is a modular lattice.
Claim: a 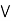 [ b
[ b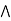 (
(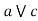 )] = (a
)] = (a 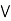 b)
b) 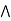 (a
(a 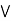 c).
c). 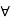 a, b,c
a, b,c 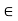 L., a
L., a 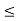 c.
c.
Let a, b, c 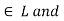 a
a 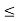 c.
c.
Consider,
a 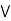 [ b
[ b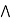 (
(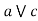 )] = a
)] = a 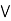 [ b
[ b 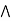 x], let x = a
x], let x = a 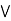 c
c
= (a 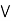 b)
b) 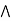 x
x 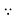 by modular property.
by modular property.
= (a 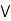 b)
b) 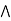 (a
(a 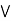 c).
c).
a 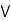 [ b
[ b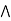 (
(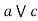 )] = (a
)] = (a 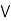 b)
b) 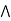 (a
(a 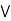 c).
c).
conversely, suppose that
a 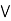 [ b
[ b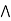 (
(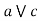 )] = (a
)] = (a 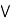 b)
b) 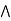 (a
(a 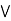 c).
c). 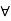 a, b, c
a, b, c 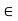 L., a
L., a 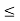 c.
c.
claim: L is modular lattice.
It is enough to prove that a 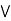 [ b
[ b 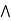 c] = (a
c] = (a 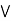 b)
b) 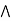 c.
c. 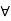 a, b, c
a, b, c 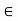 L., a
L., a 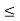 c.
c.
Let a, b, c 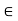 L ; a
L ; a 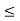 c.
c.
a 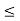 c = a
c = a 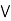 c = c
c = c
= a 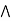 c = a.
c = a.
Consider,
a 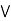 [ b
[ b 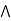 c] = (a
c] = (a 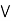 [b
[b 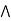 (a
(a 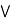 c)].
c)].
= (a 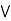 b)
b) 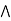 (a
(a 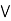 c)
c)
= (a 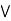 b)
b) 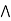 c.
c.
 a
a 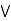 [ b
[ b 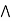 c] = (a
c] = (a 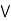 b)
b) 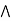 c.
c.
 L is a modular lattice.
L is a modular lattice.
Hence proved.
Example 2: every chain is a distributive lattice.
Proof: suppose L is a chain.
Let a, b, c 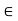 L., a
L., a 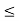 c.
c.
Claim: L is distributive lattice.
It is enough to prove that
a 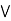 [ b
[ b 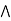 c] = (a
c] = (a 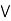 b)
b) 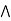 (a
(a 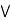 c).
c).
case 1: b 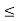 c.
c.
(a 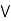 b)
b) 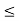 (a
(a 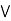 c).
c).
(a 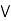 b) = (a
b) = (a 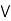 b)
b) 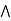 (a
(a 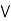 c).
c).
a 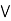 [ b
[ b 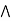 c] = (a
c] = (a 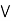 b)
b) 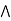 (a
(a 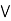 c).
c).
case 2: c 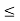 b.
b.
(a 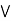 c)
c) 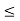 (a
(a 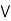 b).
b).
a 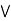 [ c
[ c 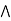 b] = (a
b] = (a 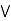 b)
b) 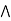 (a
(a 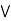 c).
c).
a 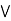 [ b
[ b 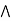 c] = (a
c] = (a 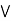 b)
b) 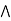 (a
(a 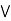 c).
c).  is commutative.
is commutative.
 every chain is a distributive lattice.
every chain is a distributive lattice.
4.1.6 Chains and anti-chains.
Definition 1: A chain is a totally ordered subset of a poset S; an antichain is a subset of a poset S in which any two distinct elements are incomparable. Now, we have two distinct concepts of a chain/antichain being “as large as possible”. One of those concepts is “not easily extendable” – that is to say, a chain or antichain which can’t have elements added to make it a larger chain/antichain:
Definition 2: A maximal chain (antichain) is one that is not a proper subset of another chain (antichain). Alternatively, a chain C is maximal in a poset (S, 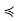 ) if no element of S − C is comparable to every element of C; an antichain A is maximal if no element of S − A is incomparable to every element of A. Our other definition of largeness is that of simply being of the greatest size in a poset.
) if no element of S − C is comparable to every element of C; an antichain A is maximal if no element of S − A is incomparable to every element of A. Our other definition of largeness is that of simply being of the greatest size in a poset.
Definition 3: A maximum or longest chain (largest antichain) is one which is of the greatest size possible. The size of the longest chain is known as a poset’s height. The size of the largest antichain is known as a poset’s width.
Example 1: A maximal chain in a finite nonempty poset must contain a maximal element of S (and a minimal element).
Poof: Suppose C ⊂ P is a maximal chain, Since (C, 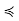 ) is a finite nonempty poset in its own right, it has some maximal element x; since C is totally ordered, the nonexistence of any y in C such that x
) is a finite nonempty poset in its own right, it has some maximal element x; since C is totally ordered, the nonexistence of any y in C such that x 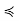 y implies that y
y implies that y 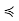 x for all y ∈ C, so x is in fact a greatest element of C (if not necessarily of S). We have two possibilities to address: x may be maximal in S, or it may not. If it is maximal, our condition has been shown. If it is not maximal, there is a z ∈ S such that x
x for all y ∈ C, so x is in fact a greatest element of C (if not necessarily of S). We have two possibilities to address: x may be maximal in S, or it may not. If it is maximal, our condition has been shown. If it is not maximal, there is a z ∈ S such that x 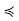 z. Then, for all y ∈ C, y
z. Then, for all y ∈ C, y 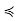 x
x 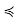 z, so
z, so
y 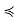 z, so C ∪ {z} is totally ordered, contradicting C’s maximality. The proof for minimal elements proceeds along similar lines.
z, so C ∪ {z} is totally ordered, contradicting C’s maximality. The proof for minimal elements proceeds along similar lines.
Example 2: The set of maximal elements of a finite poset S is a maximal antichain; likewise, the set of minimal elements of a finite poset S is a maximal antichain.
Proof. Note that this is trivially true if S is empty; henceforth, we will consider the case where S has at least one element. Let A be the set of maximal elements of S. We shall first prove that A is an antichain, and then that any augmentation of A by adding an element is not an antichain.
Consider distinct elements x, y ∈ A. Since x is a maximal element and y 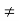 x, maximality guarantees x
x, maximality guarantees x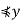 , Likewise, since y is maximal and distinct from
, Likewise, since y is maximal and distinct from
x, y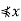 . Thus, x and y are incomparable. Since this is true of arbitrarily chosen distinct elements of A, all distinct elements of A are incomparable and A is an antichain.
. Thus, x and y are incomparable. Since this is true of arbitrarily chosen distinct elements of A, all distinct elements of A are incomparable and A is an antichain.
Now, consider z0 ∈ S −A; that is, z0 is a non-maximal element of S. We shall show that A∪ {z0} is not an antichain. Since z0 is nonmaximal, there is some 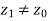 such that
such that 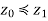 . If z1 is maximal, it is in A; if it is nonmaximal, there is a
. If z1 is maximal, it is in A; if it is nonmaximal, there is a 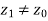 such that
such that 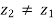 . We continue along these lines until we get either a zk that is maximal, or an infinite ascending sequence z0
. We continue along these lines until we get either a zk that is maximal, or an infinite ascending sequence z0 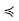 z1
z1 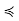 · · · The latter situation was shown last week to be impossible in a finite poset,
· · · The latter situation was shown last week to be impossible in a finite poset,
Thus, some zk is maximal, so zk ∈ A and z0 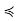 z1 · · ·
z1 · · · 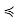 zk gives z0
zk gives z0 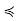 zk by transitivity. Since z0 and zk are comparable, and zk ∈ A, A ∪ {z0} is not an antichain. The proof for minimal elements proceeds along similar lines
zk by transitivity. Since z0 and zk are comparable, and zk ∈ A, A ∪ {z0} is not an antichain. The proof for minimal elements proceeds along similar lines
4.2.1 Functions and composition of functions.
Definition: A Function or mapping (Defined as f:X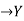 ) is a relationship from elements of one set X to elements of another set Y (X and Y are non-empty sets). X is called Domain and Y is called Codomain of function ‘f’.
) is a relationship from elements of one set X to elements of another set Y (X and Y are non-empty sets). X is called Domain and Y is called Codomain of function ‘f’.
Function ‘f’ is a relation on X and Y such that for each x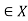 , there exists a unique
, there exists a unique 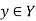 such that (x, y)
such that (x, y)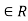 . x is called pre-image and ‘y’ is called image of function f.
. x is called pre-image and ‘y’ is called image of function f.
A function can be one to one or many to one but not one to many.
Injective /One-to-One Function: A Function f: A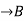 is injective or one-to-one function if for every
is injective or one-to-one function if for every 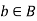 , there exists at most one
, there exists at most one 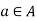 such that f(s)=t.
such that f(s)=t.
This means a function f is injective if 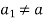 implies f (
implies f (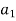 )
)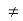 f (
f (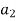 )
)
Example:
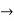
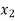
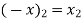
Surjective/ Onto Function: A Function f: 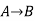 is surjective (onto) if the image of f equals its range. Equivalently, for every
is surjective (onto) if the image of f equals its range. Equivalently, for every 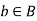 , there exists some
, there exists some 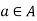 such that f(a)=b. This means that for any y in B, there exists some x in A such that y=f(x).
such that f(a)=b. This means that for any y in B, there exists some x in A such that y=f(x).
Example:
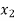
Bijective/ One-to-One Correspondent: A function f: A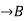 is bijective or one-to-one correspondent if and only if f is both injective and surjective.
is bijective or one-to-one correspondent if and only if f is both injective and surjective.
Composition of Functions: Two function f: A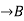 and
and 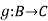 can be composed to give a composition gof. This is a function from A to C defined by (gof)(x)=g(f(x)).
can be composed to give a composition gof. This is a function from A to C defined by (gof)(x)=g(f(x)).
Example 1: Let f(x)=x+2 and g(x)=2x+1.
Here find (fog)(x) and (gof)(x).
Solution: (fog)(x)=f(g(x)) =f(2x+1) =2x+1+2=2x+3
(gof)(x)= g(f(x)) = g(x+2) = 2(x+2) +1 = 2x+5
Hence, (fog)(x)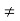 (gof)(x)
(gof)(x)
Some facts about Composition:
Example 2: Prove that a function f: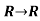 defined by f(x)=2x-3 is a bijective function.
defined by f(x)=2x-3 is a bijective function.
Solution: We have to prove this function is both injective and surjective.
If f (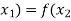 ), then
), then 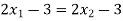 and it implies that
and it implies that 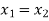
Hence, f is injective.
Here, 2x-3=y
So, x = 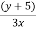 which belongs to R and f(x)=y
which belongs to R and f(x)=y
Hence, f is surjective.
Since f is both surjective and injective, we can say f is bijective.
Example 3: let 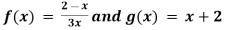 and domain of f(x) : {x/x
and domain of f(x) : {x/x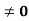 }, domain of g(x): {x/ x
}, domain of g(x): {x/ x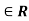 }
}
Solution: 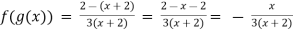
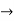 Domain of f(g(x)) = {x/x
Domain of f(g(x)) = {x/x 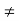 -2}
-2}
= 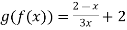 =
= 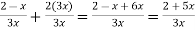
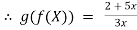
Example 4: given f(x) = x+2 and g(x) = 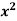 + 1 find [f o g](x) = ?
+ 1 find [f o g](x) = ?
Solution: [f o g] (x) = f [g(x)]
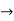 [f o g] (x) = f [ x2 + 1]
[f o g] (x) = f [ x2 + 1]
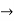 [f o g] (x) = (x2 + 1) +2
[f o g] (x) = (x2 + 1) +2
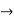 [f o g] (x) = x2 + 3.
[f o g] (x) = x2 + 3.
4.2.2 Invertible functions.
Inverse of a Function The inverse of a one-to-one corresponding function f: A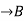 , is the function
, is the function 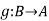 , holding the following property.
, holding the following property.
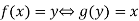
The function f is called Invertible, if its inverse function g exists.
Example:
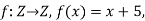
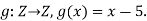
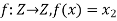
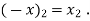
Example 1: find inverse function of the given function f(x) = 4 – 7x.
Solution: given, f(x) = 4 – 7x
Let y = 4 – 7x let y = f(x)
7x = 4 – y
X = 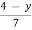 x in terms of y
x in terms of y
f-1(x) = 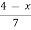 change y to x
change y to x
Example 2: f(x)= 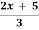 find the inverse of f(x).
find the inverse of f(x).
solution: let y = 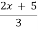 let y = f(x)
let y = f(x)
3y = 2x+5
2x+5 = 3y
2x = 3y – 5
X = 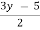 x in terms of y
x in terms of y
f-1(x) = 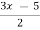
4.2.3 Pigeonhole Principle.
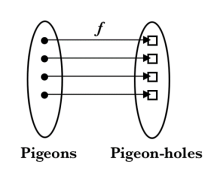
Formally, think of the pigeonhole principle as the statement about a function f from domain 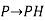 , where pigeon n flies into pigeonhole f(n), as is shown below:
, where pigeon n flies into pigeonhole f(n), as is shown below:
Figure 1. A: More pigeons than pigeonholes 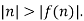
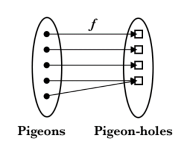
B: Same number of pigeons as pigeonholes 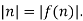
C: More pigeonholes than pigeons 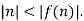
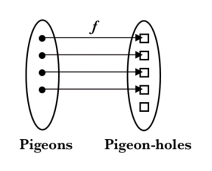
The three cases illustrate three types of functions from a domain (“pigeons”) to a codomain “pigeonholes” which can be mapped to one another:
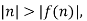
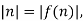
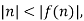
Example – 1: If (Kn+1) pigeons are kept in n pigeon holes where K is a positive integer, what is the average no. of pigeons per pigeon hole?
Solution:
Average number of pigeons per hole = (Kn+1)/n = K + 1/n
Therefore there will be at least one pigeonhole which will contain at least (K+1) pigeons i.e., ceil[K +1/n] and remaining will contain at most K i.e., floor[k+1/n] pigeons.
i.e., the minimum number of pigeons required to ensure that at least one pigeon hole contains (K+1) pigeons is (Kn+1).
Example – 2: A bag contains 10 red marbles, 10 white marbles, and 10 blue marbles. What is the minimum no. of marbles you have to choose randomly from the bag to ensure that we get 4 marbles of same colors?
Solution:
Apply pigeonhole principle.
No. of colors (pigeonholes) n = 3
No. of marbles (pigeons) K+1 = 4
Therefore the minimum no. of marbles required = Kn+1
By simplifying we get Kn+1 = 10.
Verification: ceil[Average] is [Kn+1/n] = 4
[Kn+1/3] = 4
Kn+1 = 10
i.e., 3 red + 3 white + 3 blue + 1(red or white or blue) = 10
4.2.4 Discrete numeric functions.
Definition: Discrete numeric functions are defined as,
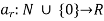 . where
. where 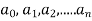 are discrete numeric functins for the values of 1, 2, …. Respectively.
are discrete numeric functins for the values of 1, 2, …. Respectively.
Example 1: 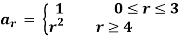 and
and 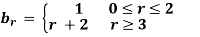
Solution: 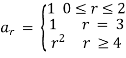 and
and 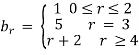
Now we show sum and product of the above numeric functions.
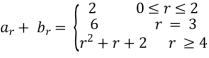 and
and 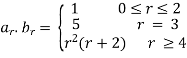
Example 2: let 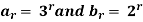 , for r
, for r 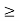 0, find the convolution of
0, find the convolution of 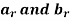
Solution: the convolution of 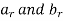 is given by,
is given by,
 =
= 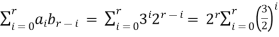
= 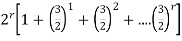
= 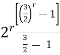
= 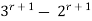 , for r
, for r 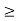 0.
0.
4.3.1 Recurrence relations.
A recurrence relation is an equation that expresses each element of a sequence as a function of the preceding ones. More precisely, in the case where only the immediately preceding element is involved, a recurrence relation has the form
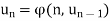 for n >0
for n >0
where
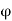 : N
: N 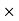 X
X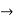 X.
X.
is a function, where X is a set to which the elements of a sequence must belong. For any 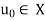 , this defines a unique sequence with
, this defines a unique sequence with 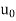 as its first element, called the initial value.
as its first element, called the initial value.
It is easy to modify the definition for getting sequences starting from the term of index 1 or higher.
This defines recurrence relation of first order. A recurrence relation of order k has the form
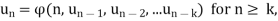
where 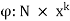 is a function that involves k consecutive elements of the sequence. In this case, k initial values are needed for defining a sequence.
is a function that involves k consecutive elements of the sequence. In this case, k initial values are needed for defining a sequence.
4.3.2 Linear recurrence relations with constant co-efficients.
A Recurrence Relations is called linear if its degree is one.
The general form of linear recurrence relation with constant coefficient is
C0 yn+r+C1 yn+r-1+C2 yn+r-2+⋯+Cr yn=R (n)
Where C0, C1, C2......Cn are constant and R (n) is same function of independent variable n.
A solution of a recurrence relation in any function which satisfies the given equation.
Example1: Solve the difference equation ar-3ar-1+2ar-2=0.
Solution: The characteristics equation is given by
s2-3s+2=0 or (s-1) (s-2) = 0
⇒ s = 1, 2
Therefore, the homogeneous solution of the equation is given by
ar=C1r+C2.2r.
Example2: Solve the difference equation 9yK+2-6yK+1+yK=0.
Solution: The characteristics equation is
9s2-6s+1=0 or (3s-1)2=0
⇒ s =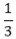 and
and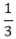
Therefore, the homogeneous solution of the equation is given by
yK=(C1+C2 k).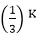
Example3: Solve the difference equation yK-yK-1-yK-2=0.
s= 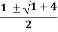 =
= 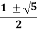
solution: the character equation is given by s2 – s-1
Therefore, the homogeneous solution of the equation is
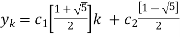 k
k
4.3.3 Total solutions.
The total solution or the general solution of a non-homogeneous linear difference equation with constant coefficients is the sum of the homogeneous solution and a particular solution. If no initial conditions are given, obtain n linear equations in n unknowns and solve them, if possible, to get total solutions.
If y(h) denotes the homogeneous solution of the recurrence relation and y(p) indicates the particular solution of the recurrence relation then, the total solution or the general solution y of the recurrence relation is given by
Y = 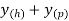
Example 1: solve the difference equation to find the total solution
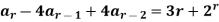 …..equation(1)
…..equation(1)
Solution: the homogenous of this equation is obtained by putting R.H.S equal to zero i.e., 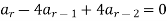
Then equation (1) can be written as,
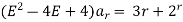
The particular solution is given as
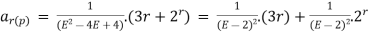
= 3.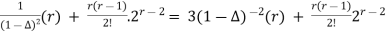
= 3(1+2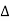 ). [r]+
). [r]+ 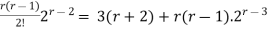
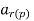 = 3(r+2) + r(r-1)2r-3
= 3(r+2) + r(r-1)2r-3
Therefore, the total solution is 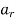 =
= 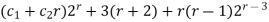 .
.
4.3.4 Applications of relations and functions.
Example 1: Suppose the weights of four students are shown in the following table.
Student | 1 | 2 | 3 | 4 |
Weight | 120 | 100 | 150 | 130 |
Solution: The pairing of the student number and his corresponding weight is a relation and can be written as a set of ordered-pair numbers.
W = {(1,120),(2,100),(3,150),(4,130)}
The set of all first elements is called the domain of the relation.
The domain of W = {1,2,3,4}
The set of second elements is called range of the relation.
The range of W = {120,100,150,130}
Example 2: Determine whether the following are functions
a) A = {(1,2), (2,3), (3,4), (4,5)}
b) B = {(1,3), (0,3), (2,1), (4,2)}
c) C = {(1,6), (2,5), (1,9), (4,3)}
Solution: a) A = {(1,2), (2,3), (3,4), (4,5)} is a function because all the first elements are different.
b) B = {(1,3), (0,3), (2,1), (4,2)} is a function because all the first elements are different. (The second element does not need to be unique)
c) C = {(1,6), (2,5), (1,9), (4,3)} is not a function because the first element, 1, is repeated.
A function can be identified from a graph. If any vertical line drawn through the graph cuts the graph at more than one point, then the relation is not a function. This is called the vertical line test.