UNIT-5
INTRODUCTION TO NUMBER THEORY.
Here are some properties of divisibility that would help you solve some divisibility questions easily without having to actually divide the numbers. These are simple to understand and easy to remember, go through these:
A division algorithm is an algorithm which, given two integers N and D, computers their quotient and/or remainder, the result of Euclidean division. Some are applied by hand, while others are employed by digital circuit designs and software. Division algorithms fall into two min categories: slow division and fast division.
Example 1: Using division algorithm solve the following equation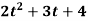 
.
Solution: =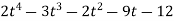 
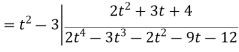
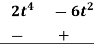
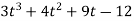
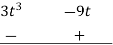
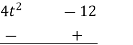
0
Example 2: Use the division algorithm to find q&r such that a= bq +r where
1): a =25 and b =7
2): a =9 and b =4
3): a =203 and b = 8
4): a=150 and b=6
Solution:
1). a = bq+r 2). a =bq+r 3). a = bq+r 4). a = bq+r
25 = 7q+6 9 = 4q+r 203 = 8q+r 150= 6q+r
25 = 7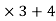
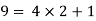
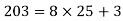
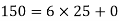
The greatest common divisor (GCD), also called the greatest common factor, of two number is the largest number that divides them both. For instance the greatest common factor of 20 and 15 is 5, since 5 divides both 20 and 15 and l=no larger number has this property. The concept is easily extended to sets of more than two numbers: the GCD of a set of numbers is the largest number dividing each of them.
The GCD is used for a variety of applications in number theory, particularly in modular arithmetic and thus encryption algorithms such as RSA. It is also used for simpler applications, such as simplifying fractions. This makes the GCD a rather fundamental concept to number theory, and as such anumber of algorithms have been discovered efficiently compute it.
Example 1: Find the greatest common divisor (or HCF) of 128 and 96.
Solution: By the method of prime factorization,
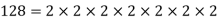
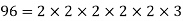
HCF (128,96) =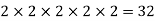 
(Or)
By the method of division,
96)128(1
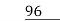
32)96(3
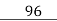
0
Hence, 32 is the HCF of 128 and 96
(or)
By Euclid’s division algorithm,
128 = 96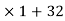
96 = 32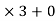
Hence, the HCF of 128 and 96 is 32.
Example 2: Two rods are 22 m and 26 m long. The rods are to be cut into pieces of equal length. Find the maximum length of each piece.
Solution: HCF or GCD is the required length of each piece.
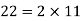
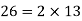
HCF or the greatest common divisor = 2
Hence, the required maximum length of each piece is 2 m.
Example 3: Find the greatest common factor of 24, 148 and 36.
Solution: Prime factorization of given numbers is
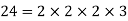
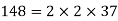
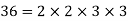
Greatest common factor =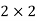 
= 4.
The greatest common divisor of integers a and b, denoted by gcd (a,b), is the largest integer that divides (without remainder) both a and b. So, for Example.
Example:
gcd (15,5) = 5, gcd (7,9) =1, gcd (12,9) = 3, gcd (81,57) =3.
The gcd of two integers can be found by repeated application of the division algorithm, this is known as the Euclidean algorithm. You repeatedly divide the divisor by the remainder until the remainder is 0. The gcd is the last non-zero remainder in this algorithm. The following example shows the algorithm.
Finding the gcd of 81 and 57 by the Euclidean Algorithm:
81 = 1(57) + 24
57 = 2(24) + 9
24 = 2(9) + 6
9 = 1(6) + 3
6 = 2(3) + 0
It is well known that if the gcd (a,b) = r then there exists integers p and s so that:
p(a)+s(b) = r.
By reversing the steps in the Euclidean Algorithm, it is possible to find these integers p and s.
81 = 1(57) + 24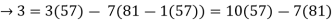 
57 = 2(24) + 9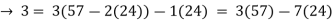 
24 = 2(9) + 6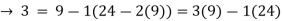 
9 = 1(6) + 3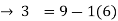 
6 = 2(3) + 0
So, we have found p = -7 and s = 10.
Extended Euclidean Algorithm: The procedure we have followed above is a bit messy because of all the back substitutions we have to make. It is possible to reduce the amount of computation involved in finding p and s by doing some auxiliary computations as we go forward in the Euclidean algorithm (and no back substitutions will be necessary). This is known as the Extended Euclidean Algorithm.
Example 1: m = 65, n = 40
Step 1: The (usual) Euclidean algorithm:
(1): 65 = 1.40 + 25
(2): 40 = 1.25+15
(3): 25 = 1.15+10
(4): 15 = 1.10 + 5
10 = 2.5
Therefore gcd (65,40) = 5.
Step 2: Using the method of back substitution:
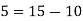
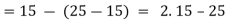
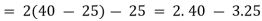
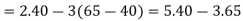
Conclusion: 65(-3) + 40(5) = 5.
Example 2: Let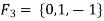 
be the field of integers modulo 3, a(x) = 
,
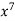b(x) =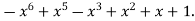 
Then the behavior of Euclid’s algorithm is given in table.
An Example of Euclid’s algorithm.
i |
 |  |  |  |
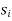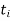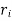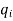-1 0 1 2 3 4 5 | 1 0 1 x 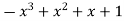 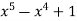 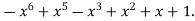 | 0 1 x+1 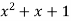 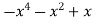 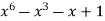 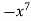 | 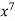 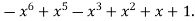 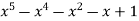 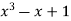 x 1 0 | - - -x-1 -1 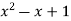 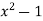 x |
Proposition: Except for 0 and 1, every natural number is a product of finitely many prime numbers, its prime factors. Here ‘products’ with only one factor are allowed. This prime factorization is, up to the order of the factors, unique.
To prove the uniqueness of prime factorization we suppose, to the contrary, that there is a number with two different prime factorizations. Let p be the least such number with prime factorizations p =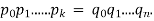 
We have
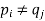for all I and j, since any common factor could be divided out to give a smaller natural number p with two different prime factorizations, in contradiction to the choice of p.
We can suppose that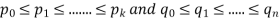 
as well as 
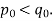Set q: = 
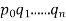. Then 
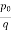and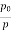 
, hence 
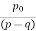. Consequently, we have the prime factorization.
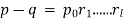
For some prime numbers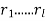 
. Because p-q = (
)
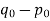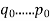, the number p-q is positive. Write 
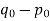as a product of prime numbers: 
= 
,
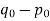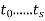Then
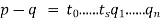
Is a second prime factorization of p-q. It is clear that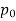 
does not divide 
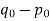. Hence, we have two prime factorizations of p-q, only one of which contains 
.
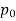Because 0<p-q<p, this contradicts the minimality of p.
Example 1: Find the prime factors of 1240.
Steps | Prime Factors | Product |
Step 1: Divide by 2 | 2 | 1240  |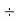
Step 2: Divide by 2 | 2 | 620  |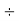
Step 3: Divide by 2 | 2 | 310  |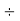
Step 4: Divide by 5 | 5 | 155  |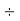
Step 5: Divide by 31 | 31 | 31  |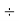
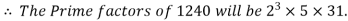
Example 2: Find the prime factors of 544:
Steps | Prime Factors | Product |
Step 1: Divide by 2 | 2 | 544  |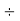
Step 2: Divide by 2 | 2 | 272  |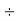
Step 3: Divide by 2 | 2 | 136  |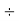
Step 4: Divide by 2 | 2 | 68  |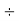
Step 5: Divide by 2 | 2 | 34  |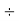
Step 6: Divide by 17 | 17 | 17  |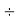
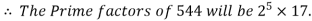
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure (such as group, ring, or vector space) that is compatible with the structure in the sense that algebraic operations done with equivalent elements will yield equivalent elements. Every congruence relation has a corresponding quotient structure, whose elements are the equivalence classes (or congruence classes) for the relation.
Example 1: The prototypical example of a congruence relation is congruence modulo n on the set of integers. For a given positive integer n, two integers a and b are called congruent modulo n, written
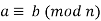
if a-b is divisible by n (or equivalently if a and b have the same remainder when divided by n).
for example, 37 and 57 are congruent modulo 10.
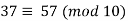
Since 37 – 57 = -20 is a multiple of 10, or equivalently since both 37 and 57 have a remainder of 7 when divided by 10. Congruence moduli n (for a fixed n) is compatible with both addition and multiplication on the integers. That is, if
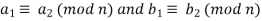
Then,
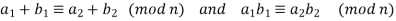
The corresponding addition and multiplication of equivalence classes is known as modular arithmetic. From the point of view of algebra, congruence modulo n is a congruence relation on the ring of integers, and arithmetic modulo n occurs on the corresponding quotient ring.
Example 2:
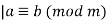
Remember that this means that m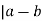
Called “congruence modulo m”
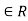
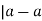
a-a = 0, which is divisible by m
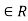
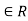
(a, b) means that m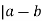
Or that km = a-b. negating that, we get b-a = -km
Thus, m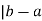
, so (b, a) 
(a, b) means that m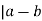
, or that km = a-b
(b, c) means that m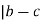
, or that lm = b-c
(a, c) means that m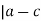
, or that nm = (a-b) + (b-c)
Or (k +l) m = a-c
Thus, m divides a-c, where n = k +l
Thus, congruence modulo m is an equivalence relation.
Definition: Modular arithmetic is the branch of arithmetic mathematics related with the “mod” functionality. Basically, modular arithmetic is related with computation of “mod” of expressions. Expressions may have digits and computational symbols of addition, subtraction, multiplication, division or any other. Here we will discuss briefly about all modular arithmetic operations.
Quotient Remainder Theorem:
It states that, for any pair of integers a and b (b is positive), there exists two unique integers q and r such that:
a = b x q + r
where 0 <= r < b
modular addition:
(a+b) mod m = ((a mod m)+(b mod m))mod m.
Modular multiplication:
(a * b) mod m = ((a mod m) * (b mod m)) mod m.
Modular Inverse:
The modular inverse of a mod m exists only if a and m are relatively prime i.e. gcd(a, m) = 1.
Hence, for finding inverse of a under modulo m,
if (a x b) mod m = 1 then b is modular inverse of a.
Modular Exponentiation:
Finding a^b mod m is the modular exponentiation. There are two approaches for this – recursive and iterative
Example 1: find modulo addition of the following: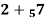 
Solution: (2 + 7) mod 5 = 9 mod 5 = 4
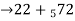
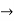(22 + 72) mod 5 = 4
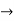in other way we can write as,
22 mod 5+72 mod 5 = 2 mod 5 + 2 mod 5
= 4 mod 5 = 4.
Example 2: find modular inverse of 600
Solution: by applying Euclidean algorithm.
600 = 43.15+15
43 = 15.2+ 13
15 = 13 .1+2
13 = 2.6 +1
Then work backwards:
1 = 13 -2.6
= 13-(15-13.1)6 = 13.7 – 15.6
= (43 – 15.2)7 – 15.6 = 43.7 – 15.20
= 43.7 – (600-43. 15)20 = 43. 307 – 600.20
Finally take mod 600:
1 
43.307
Thus t = 307 is an inverse.
Exercise:
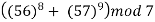
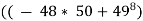
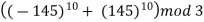
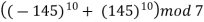
Definition: In number theory, Euler's totient function counts the positive integers up to a given integer n that are relatively prime to n. It is written using the Greek letter phi as φ(n) or ϕ(n), and may also be called Euler's phi function.
In other terms: A function f is homogeneous of degree n if
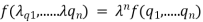
theorem: if f is homogeneous of degree n then
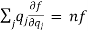
Proof:
The proof follows by differentiating equation (1) w.r.to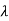 
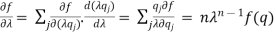
By substituting in the above equation with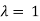 
we get the Euler theorem.
Example 1: solve using euler’s phi-function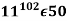 
Solution: we check the given number using euler’s phi-function
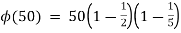
= 50*(1/2)(4/5)
= 20.
So,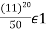 
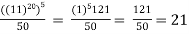
Note: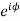 
= cos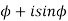
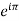+1 = 0
Example 2: What is the Euler number of 20?
Solution: Now, the factorization of 20 is 2,2,5. It has only two prime factors i.e., 2 and 5.
So, the Euler number of 20 will be
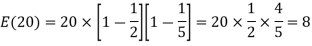
Hence, there are 8 numbers less than 20, which are co-prime to it. Cross check: Numbers co-prime to 20 are 1,3,7,9,11,13,17 and 19,8 in number.
Example 3: What is the remainder when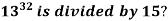 
Solution: Now in this case the Euler number of 15 is 8
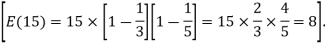
Now the Numerator can also be written as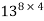 
. Thus, the remainder in this case will be 1.
Fermat's little theorem is the basis for the Fermat primality test and is one of the fundamental results of elementary number theory. The theorem is named after Pierre de Fermat, who stated it in 1640. It is called the "little theorem" to distinguish it from Fermat's last theorem.
Statement: Fermat’s little theorem states that if p is a prime number, then for any integer a, the number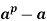 
is an integer multiple of p.
Proof: First, we will show that the theorem is true for all positive integers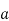 
by induction. The base case (when 
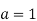) is obviously true: 
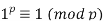. For the inductive hypothesis; assume that 
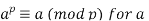certain integer a. The goal is to show that 
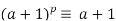(mod p).
By the binomial theorem:
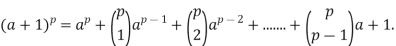
But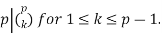 
Because 
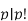but 
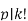and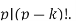 
So the middle terms vanish mod p:
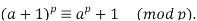
Substituting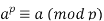 
by the inductive hypothesis gives
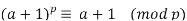
So the result holds for all positive a by induction. But every integer is congruent mod p to a positive integer, so the result holds for every integer.
Example 1: Let p>5 be a prime number, and let k be any positive integer<p. Show that the decimal expansion of k/p consists of p-1 repeating decimal digits.
Solution: By Fermat’s theorem,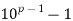 
is divisible by p, say pa =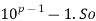 
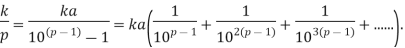
Since ka<pa<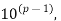
write ka as a (p-1) digit number (with 0s in the front if necessary). The above expansion shows that the (p-1) digit number will repeat.
For example, let k = 2 and p = 7. Then a =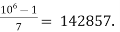 
So ka = 285714. So
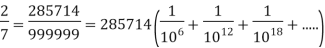
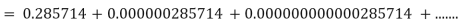
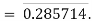
Example 2: Solve 5x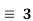
(mod 17) using Fermat’s little theorem.
Solution: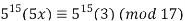 
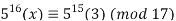
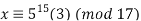
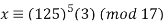
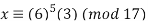
Two numbers are called additive inverse if their sum is zero.
Two numbers are called multiplicative inverse if their product is one
Example 1: How do you Simplify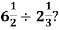 
Solution: The first step to simplifying this expression is to covert the mixed fractions into improper fractions. This is done by multiplying the integer or whole number part of the fraction by the correct form of 1 and then adding it to the fraction:
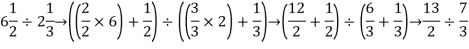
This can now be rewritten as:
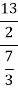
The rule for dividing fraction is:
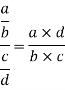
Using this rule on our expression gives:
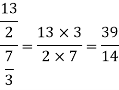
Example 2: How do you solve 4(x-1)- (x+2) =12?
Solution: 4(x-1)- (x+2) =12
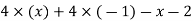
4x-4-x-2 =12
4x -x -2 -4 =12
3x -6 = 12
3x = 12+6
3x = 18
x =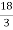 
x = 6.
Example 3: Add the rational number 2/3 and its additive inverse.
Solution:
Step 1: The additive inverse of 2/3 is -2/3
Then, we have to find (2/3)+(-2/3)
Step 2: In the above addition since the two rational numbers have different signs we have to find absolute difference of them without the actual signs.
|2/3-2/3|= |0|=0
So we write (2/3) + (-2/3) = 0
Statement: suppose 
are pair wise relatively rime positive integers, and suppose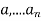 
are integers. Then the system of congruencies are given by
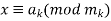, for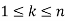 
has a unique solution x modulo M=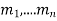 
such that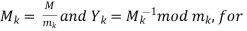 
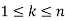
proof: Let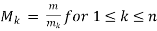 
gcd (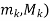
= 1 and 
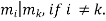Hence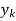 
is an inverse of 
.
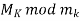now,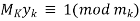 
and
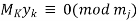for all 
.
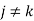Let x =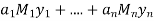 
then
X 
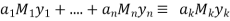
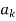(mod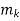 
) for all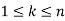 
Example 1: Solve the equations: x = 3mod 6, x =6 mod 7, x = 10 mod 11.
 |  |  |  |
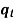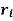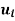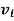0 0 9 2
| 66 7 3 1 | 0 1 -9 19 | 1 0 1 -2 |
Solution:
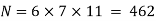
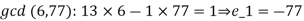
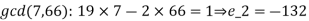
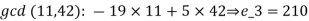
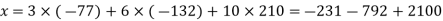
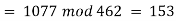
Example 2: Consider the 3 congruences,
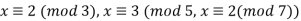
Solution: Let m = 3.5.7 = 105,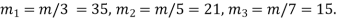 
We see that,
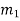
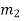
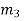
Hence,
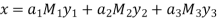
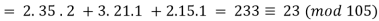
We have shown that 23 is the smallest positive integer that is a simultaneous solution.
