UNIT-6
Algebraic structures.
Semi-group: An algebraic structure which satisfies closure and associative property is said to a semi-group
i.e.,
Closure: (a*b) S to s for all a,b 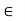 to S
to S
Associative property: a*(b*c)  to S for all a,b,c
to S for all a,b,c 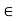 to S
to S
Monoids: An algebraic structure which satisfies closure, associative property and identity is said to be a monoid.
Closure: (a*b) 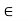 to S for all a,b
to S for all a,b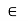 to S
to S
Associative property: a*(b*c) to  S for all a,b,c
S for all a,b,c 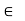 to s.
to s.
Identity element: There exists e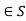 such that e*a = a*e
such that e*a = a*e 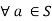
Example1: Let S=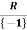 . Define * on S by a*b =a+ b+ a b
. Define * on S by a*b =a+ b+ a b
(a) Show that * is a binary operation on S.
(b) Show that [S, *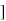 is a group.
is a group.
(c) Find the solution of the equation 2*x*3= 7 in S
Solution: (a) We must show that S is closed under *, that is , that a+b+ab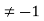 for a,b
for a,b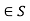 .Now a+b+ab=-1 if and only if 0=ab+a+b+1=(a+1)(b+1).This is the case if and only if either a=-1 or b = -1 , which is not the case for a,b
.Now a+b+ab=-1 if and only if 0=ab+a+b+1=(a+1)(b+1).This is the case if and only if either a=-1 or b = -1 , which is not the case for a,b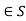 .
.
(b) We have a*(b*c) = a*(b+c+bc) = a+(b+c+bc)+a(b+c+bc)=a+b+c+ab+ac+bc+abc and (a*b)*c = (a+b+ab)*c =(a+b+ab)+c+(a+b+ab) = a+b+c+ab+ac+bc+abc. Thus * is associative. Note that 0 acts as identity element for *, since 0*a =a*0=a.
Also, 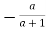 acts as inverse of a , for a*
acts as inverse of a , for a* 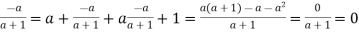
Thus [s, *] is a group.
(c)Because the operation is commutative, 2*x*3=2*3*x=11*x. Now the inverse of 11 is 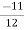 ,by part(b). from 11*x=7, we obtain
,by part(b). from 11*x=7, we obtain
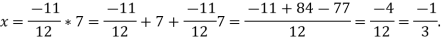
Example 2: Let G be a group with a finite number of elements. Show that for any 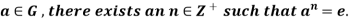
Solution: Let G has m element, Then the elements e, a,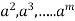 are not all different, since G has only m elements. If one of e, a,
are not all different, since G has only m elements. If one of e, a, is e, then we are done. If not, then we must have
is e, then we are done. If not, then we must have 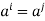 where i<j, Repeated left cancellation of a yields e=
where i<j, Repeated left cancellation of a yields e=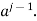
Groups: An algebraic structure which satisfies closure, associative, identity and inverse properties is said to be a group.
Closure: (a*b)  to S for all a, b
to S for all a, b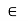 to S
to S
Associative property: a*(b*c) to 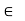 S for all a, b, c
S for all a, b, c  to s.
to s.
Identity property: There exists e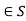 such that e*a = a*e
such that e*a = a*e 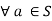
Inverse property: there exists a, a-1 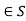 such that a * a-1 = a,
such that a * a-1 = a, 
Abelian group: An Abelian group is a set A with a binary operation ◦ satisfying the following conditions:
(A1) For all a, b, c ∈ A, we have a ◦ (b ◦ c) = (a ◦ b) ◦ c (the associative law).
(A2) There is an element e ∈ A such that a ◦ e = a for all a ∈ A.
(A3) For any a ∈ A, there exists b ∈ A such that a ◦ b = e.
(A4) For all a, b ∈ A, we have a ◦ b = b ◦ a (the commutative law).
Example 1: Any finite Abelian group is isomorphic to a direct sum of cyclic groups.
Proof: We need more than this, because two different direct sums may be isomorphic. For example, C2 ⊕C3  C6.
C6.
(If a and b are generators of the summands, then 2a = 3b = 0, and successive multiplies of (a, b) are (a, b), (0,2b), (a,0), (0, b), (a,2b), and (0,0).)
There are two standard resolutions of this problem.
(a) An Abelian group is in Smith canonical form if it is written as Cn1 ⊕··· ⊕Cnr, where n1..., nr are integers greater than 1 and ni divides ni+1 for 1 ≤ i ≤ r –
(b) An Abelian group is in prime-power canonical form if it is written as
Cq1 ⊕··· ⊕Cqr, where q1, …., qr are rare prime powers greater than 1.
Example 2: (a) Any finite Abelian group can be written in Smith canonical form. If two groups in Smith canonical form are isomorphic, then the multisets of orders of the cyclic factors are equal.
Proof: To convert Smith into prime-power and vice versa, use the fact that if n =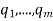 where
where 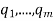 are powers of distinct prime numbers, then
are powers of distinct prime numbers, then
Cn 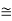 C
C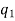 ⊕··· ⊕C
⊕··· ⊕C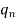 . Thus, from Smith to prime-power, simply factorise the orders of the cyclic factors. From prime-power to Smith, gather up the largest power of each prime and multiply them; then repeat until nothing remains. For example, the group C4 ⊕C12 ⊕C36 is in Smith canonical form; the group C4 ⊕C4 ⊕C4 ⊕C3 ⊕C9 is in prime-power canonical form; and these two groups are isomorphic.
. Thus, from Smith to prime-power, simply factorise the orders of the cyclic factors. From prime-power to Smith, gather up the largest power of each prime and multiply them; then repeat until nothing remains. For example, the group C4 ⊕C12 ⊕C36 is in Smith canonical form; the group C4 ⊕C4 ⊕C4 ⊕C3 ⊕C9 is in prime-power canonical form; and these two groups are isomorphic.
A permutation group is a finite group G whose elements are permutations of a given set and whose group operation is composition of permutations in G . Permutation groups have orders dividing n!
Two permutations form a group only if one is the identity element and the other is a permutation involution, i.e., a permutation which is its own inverse (Skiena 1990, p. 20). Every permutation group with more than two elements can be written as a product of transpositions.
Cosets: Cosets are a basic tool in the study of groups; for example, they play a central role in Lagrange's theorem that states that for any finite group G, the number of elements of every subgroup H of G divides the number of elements of G. Cosets of a particular type of subgroup (normal subgroup) can be used as the elements of another group called a quotient group or factor group. Cosets also appear in other areas of mathematics such as vector spaces and error-correcting codes.
Example 1: let f and g be two permutation a X. then f=g if only if f(x) =g(x) for all x in X.
Where f = 1 2 3 4 and g = 3 2 1 4
Solution: we re write the values of f and g by using permutation combinations, we get f = 2 3 4 1 and g = 4 3 2 1
Evidently f (1) = 2 = g (1)
f (2) = 3=g (2)
f (3) = 4=g (3)
f (4) = 1=g (4)
thus, f(x) = g(x) for all x E = {1, 2, 3, 4}
which implies that f(x) =g(x).
Example 2: The group Z6 into cosets of the subgroup H = {0, 3}
solution: one coset is {0, 3} itself.
select 1 in z6 but not in {0, 3}. the coset containing 1 is 1+ {0, 3} = (1, 4}
similarly, select 2 in z6 but not in {0, 3} or {1, 4}, the co-set containing 2 is
2 + {0, 3} = {2, 5}
since {0, 3}, {1, 4} and {2, 5} exhaust all of z6 are all cosets.
Example 3: Let H be the subgroup 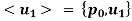 of
of 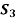 . Find the partitions of
. Find the partitions of  .Into left cosets of H, and the partition into right cosets of H. (See the table for the symmetric group
.Into left cosets of H, and the partition into right cosets of H. (See the table for the symmetric group 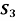 in the next slide.
in the next slide.
Solution: For the partition into left cosets, we have


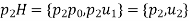
The partition into right cosets is
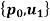
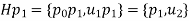
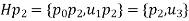
Since 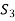 is not abelian, the partition into left cosets of H is different from the partition into right cosets.
is not abelian, the partition into left cosets of H is different from the partition into right cosets.
Normal Sub Group: A Subgroup N of a group G is called a Normal Subgroup of G if it is invariant under conjugation, that is the conjugation of an element of N by an element of G is always in N. The usual notation for this relation is N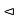 G, and the definition may be written in symbol as
G, and the definition may be written in symbol as
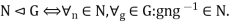
Example 1: The following are three equivalent conditions for a subgroup H to be a normal subgroup of a group G.
1.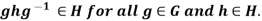
2.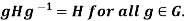
3.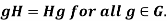
Proof : (1)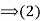 Suppose that H is a subgroup of G such that
Suppose that H is a subgroup of G such that 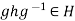 for all g
for all g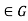 and all h
and all h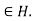 Then
Then 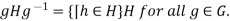
We claim that actually 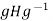 =H.We must show that H
=H.We must show that H for all g
for all g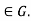
Let h . Replacing g by
. Replacing g by 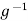 in the relation
in the relation 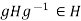 , we obtain
, we obtain 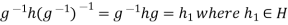 .
.
Consequently, 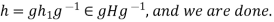
(3)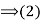 Suppose that gH=Hg for all g
Suppose that gH=Hg for all g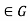 . Then
. Then 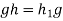 , So
, So 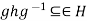 for all g
for all g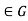
And all 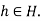 By the preceding paragraph, this means that
By the preceding paragraph, this means that 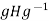 =H for all g
=H for all g .
.
(2)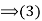 Conversely , if
Conversely , if 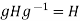 for all g
for all g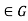 then
then 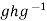 =
= gH
gH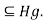 But also,
But also, 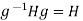 giving
giving 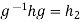 ,so that hg=g
,so that hg=g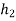 and Hg
and Hg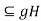 .
.
Example 2: If f: G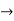 H is a homomorphism, define the kernel of f as
H is a homomorphism, define the kernel of f as
Ker f = 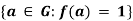 ;
;
Solution: Suppose that ker f is a normal sub-group of G. For if a 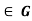 and b
and b 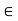 ker f, we must show that aba-1 belongs to ker f.
ker f, we must show that aba-1 belongs to ker f.
But f (aba-1) = f(a). f (b). f (a-1) = f(a)(1)f(a)-1 = 1.
Conversely, every normal sub-group is the kern el of a homomorphism.
To see this, suppose that N 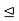 G, and let H be the quotient group G/N. Define the map
G, and let H be the quotient group G/N. Define the map 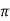 : G
: G G/N by
G/N by 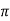 (a) = aN;
(a) = aN;
Then 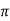 is called the natural or canonical map.
is called the natural or canonical map.
Since,
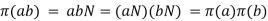
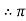 is a homomorphism.
is a homomorphism.
The kernel of 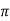 is the set of all a
is the set of all a 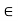 G, such that,
G, such that,
aN = N(=1N), or equivalently, a 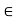 N.
N.
thus, ker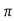 = N.
= N.
Codes: In mathematics coding theory is called as algebraic coding theory, deals with the design of error-correcting codes for the reliable transmission of information across noisy channels. It makes use of classical and modern algebraic techniques involving finite fields, group theory, and polynomial algebra.
Group code: In coding theory, group codes are a type of code. Group codes consist of n linear block codes which are subgroups of 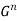 , where G is a finite Abelian group.
, where G is a finite Abelian group.
A systematic group code C is a code over 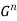 of order
of order  defined by n-k homomorphisms which determine the parity check bits. The remaining k bits are the information bits themselves.
defined by n-k homomorphisms which determine the parity check bits. The remaining k bits are the information bits themselves.
Example 1: The code with generator matrix:
G= 
Solution: The given generator matrix has code-words a follows,
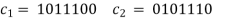
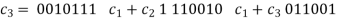

And it is cyclic because the right shifts have the following impacts
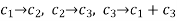
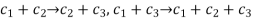
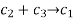
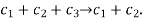
Example 2: Solve the following generator matrix.
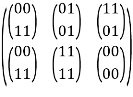
Solution: The given generator matrix can be written as,
The elements of this matrix are 2 2 matrices which are endomorphisms.
2 matrices which are endomorphisms.
In this scenario, each code-word can be represented as,
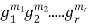 where
where  are the generators of G.
are the generators of G.
Ring: A Ring 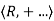 is a set R together with two binary operations + and ..., called addition and multiplication, defined on R such that the following axioms are satisfied
is a set R together with two binary operations + and ..., called addition and multiplication, defined on R such that the following axioms are satisfied
(1)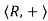 is an abelian group,
is an abelian group,
(2) Multiplication is associative,
(3) For all a, b, c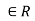 ,the left distributive law, a.(b+c) = a.b + a.c and the right distributive law (a +b).c= a.c+ b.c hold.
,the left distributive law, a.(b+c) = a.b + a.c and the right distributive law (a +b).c= a.c+ b.c hold.
Integral Domains: We know that the product of any two non-zero integers is always nonzero. But this may not be the case of arbitrary rings. For example, consider the ring 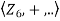 . Note that product of two nonzero elements may be zero in this ring, for instance 2.3=0 in
. Note that product of two nonzero elements may be zero in this ring, for instance 2.3=0 in 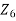 . We call these type of elements as 0 divisors.
. We call these type of elements as 0 divisors.
Field: A nonzero commutative ring in which every nonzero element has a multiplicative inverse is called a field.
Example1: The cancellation laws hold in a ring R if and only if R has no divisors of 0.
Proof : Assume that R is a ring in which the cancellation laws hold and let ab=0 for some a,b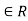 .If a
.If a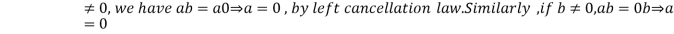 by right cancellation law .Thus R has no divisors of 0, if the cancellation laws hold in R.
by right cancellation law .Thus R has no divisors of 0, if the cancellation laws hold in R.
Conversely, suppose that R has no divisors of 0, and suppose that ab=ac, with a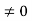 . Since a
. Since a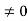 and since R has no divisors of 0, we have 0=ab-ac=a(c)
and since R has no divisors of 0, we have 0=ab-ac=a(c) 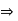 b-c =0
b-c =0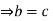 .In similar way, b a=ca with a
.In similar way, b a=ca with a . Thus, if R has no divisors of 0, The cancellation laws hold in R.
. Thus, if R has no divisors of 0, The cancellation laws hold in R.
Example 2: Every field F is an integral domain.
Proof: Let 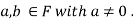 Assume that ab=0.Since
Assume that ab=0.Since 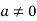 ,the multiplicative we
,the multiplicative we
inverse 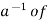 a exists, multiplying the above equation on both sides by
a exists, multiplying the above equation on both sides by  , weget
, weget
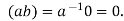 his implies, 0=
his implies, 0= b=eb=b, which shows that F has
b=eb=b, which shows that F has
no divisors of 0. Since F is a field, in particular F is a commutative ring with unity, and we showed that F has no divisors of 0. Hence F is an integral domain.
We know that Z is an integral domain, but not a field. We next prove that finite integral domains are fields.
Example 3: Consider the map det of 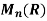 into R where det(A) is the determinant of the matrix A for A
into R where det(A) is the determinant of the matrix A for A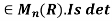 a ring homomorphism? Justify your answer.
a ring homomorphism? Justify your answer.
Solution: Because det(A+B) need not equal det(A)+det(B) , we say that det is not a ring homomorphism .For example ,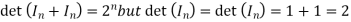
Reference Books: