Unit-4
Probability and Probability Distribution
Probability is the study of chances. Probability is the measurement of the degree of uncertainty and therefore, of certainty of the occurrence of events.
Some important definitions-
Random experiment-
An experiment in which all the possible outcomes are known in advance but we cannot predict which of them will occur when we experiment.
Example-‘Throwing a die’ and ‘Drawing a card from a well-shuffled pack of 52 playing cards ‘are examples of a random experiment
Sample space-
Set of all possible outcomes of a random experiment is known as sample space and is usually denoted by S.
Example-
1. If we toss a coin then the sample space is
S = {H, T}, where H and T denote head and tail respectively and n(S) = 2
2. If a coin is tossed thrice or three coins are tossed simultaneously, then the sample space is
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT} and n(S) = 8.
3. If a coin is tossed 4 times or four coins are tossed simultaneously then the sample space is
S = {HHHH, HHHT, HHTH, HTHH, THHH, HHTT, HTHT, HTTH, THHT,
THTH, TTHH, HTTT, THTT, TTHT, TTTH, TTTT} and n(S) = 16.
Sample point-
Each outcome of an experiment is visualized as a sample point in the sample space.
Example- If a die is thrown twice, then getting (1, 1) or (1, 2) or (1, 3) or…or (6, 6) is a sample point.
Event-
A set of one or more possible outcomes of an experiment constitutes what is known as an event. Thus, an event can be defined as a subset of the sample space
Exhaustive cases-
The total number of possible outcomes in a random experiment is called the exhaustive cases
Example-If we throw a die then the number of exhaustive cases is 6 and the sample space, in this case, is {1, 2, 3, 4, 5, 6}
Favourable cases-
The cases which favour the happening of an event are called favourable cases
Example-For the event of getting an even number in throwing a die, the number of favourable cases is 3 and the event, in this case, is {2, 4, 6}.
Mutually exclusive cases-
Cases are said to be mutually exclusive if the happening of any one of them prevents the happening of all others in a single experiment
Equally likely cases-
Two events are said to be ‘equally likely’ if one of them cannot be expected in preference to the other.
Example-if we draw a card from a well-shuffled pack, we may get any card, then the 52 different cases are equally likely.
Odds in favour of an event and odds against an event-
If the number of favourable cases is ‘m’ and the number or not favourable cases are ‘n’.
Then-
1. Odds in favour of the event = m/n
2. Odds against the event = n/m
The classical definition of probability-
Suppose there are ‘n’ exhaustive cases in a random experiment that is equally likely and mutually exclusive.
Let ‘m’ cases are favourable for the happening of an event A, then the probability of happening event A can be defined as-
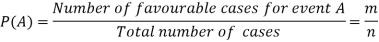
The probability of non-happening of the event A is defined as-
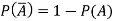
Note- Always remember that the probability of any events lies between 0 and 1.
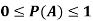
Example: A bag contains 7 red and 8 black balls then find the probability of getting a red ball.
Sol.
Here total cases = 7 + 8 = 15
According to the definition of probability,
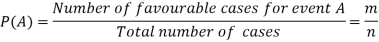
So that, here favourable cases- red balls = 7
Then,
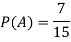
Addition and multiplication law of probability-
Addition law-
If 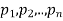 are the probabilities of mutually exclusive events, then the probability P, that any of these events will happen is given by
are the probabilities of mutually exclusive events, then the probability P, that any of these events will happen is given by 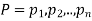
Note-
If two events A and B are not mutually exclusive then the probability of the event that either A or B or both will happen is given by-
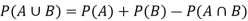
Example: A box contains 4 white and 2 black balls and a second box contains three balls of each colour. Now a bag is selected at random and a ball is drawn randomly from the chosen box. Then what will be the probability that the ball is white?
Sol.
Here we have two mutually exclusive cases-
1. The first bag is chosen
2. The second bag is chosen
The chance of choosing the first bag is 1/2. And if this bag is chosen then the probability of drawing a white ball is 4/6.
So that the probability of drawing a white ball from the first bag is-
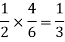
And the probability of drawing a white ball from the second bag is-
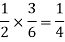
Here the events are mutually exclusive, then the required probability is-
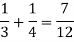
Example-25 lottery tickets are marked with the first 25 numerals. A ticket is drawn at random.
Find the probability that it is a multiple of 5 or 7.
Sol:
Let A be the event that the drawn ticket bears a number multiple of 5 and B be the event that it bears a number multiple of 7.
So that
A = {5, 10, 15, 20, 25}
B = {7, 14, 21}
Here, as A  B =
B = 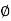 ,
,
A and B are mutually exclusive
Then,
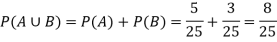
Multiplication law-
For two events A and B-
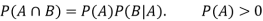
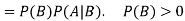
Here 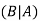 is called conditional probability of B given that A has already happened.
is called conditional probability of B given that A has already happened.
Now-
If A and B are two independent events, then-
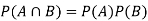
Because in the case of independent events- 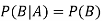
Example: A bag contains 9 balls, two of which are red three blue, and four black.
Three balls are drawn randomly. What is the probability that-
1. The three balls are of different colours
2. The three balls are of the same colours.
Sol.
1. Three balls will be of a different colour if one ball is red, one blue and one black ball are drawn-
Then the probability will be-
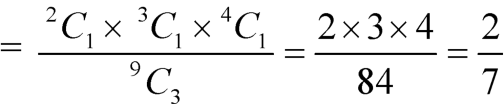
2. Three balls will be of the same colour if one ball is red, one blue and one black ball are drawn-
Then the probability will be-
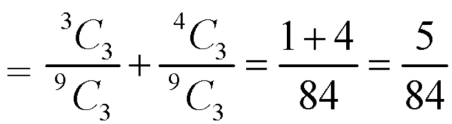
Example: A die is rolled. If the outcome is a number greater than three. What is the probability that it is a prime number?
Sol.
The sample space is- S = {1, 2, 3, 4, 5, 6}
Let A be the event that an outcome is a number that is greater than three and B be the event that it is a prime.
So that-
A = {4, 5, 6} and B = {2, 3, 5} and hence 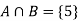
P(A) = 3/6, P(B) = 3/6 and 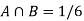
Now the required probability-
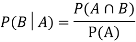
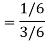
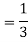
Example: Two cards are drawn from a pack of playing cards in succession with the replacement of the first card. Find the probability that both are the cards of heart.
Sol.
Let A be the event that the first card drawn is a heart and B be the event that the second card is a heart card.
As the cards are drawn with replacement,
Here A and B are independent and the required probability will be-
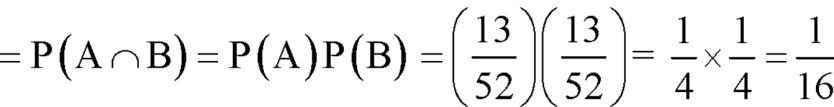
Example: Two male and female candidates appear in an interview for two positions in the same post. The probability that the male candidate is selected is 1/7 and the female candidate selected is 1/5.
What is the probability that-
1. Both of them will be selected
2. Only one of them will be selected
3. None of them will be selected.
Sol.
Here, P (male’s selection) = 1/7
And
P (female’s selection) = 1/5
Then-
1.

2.

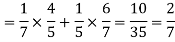
3.

Example: A can hit a target 3 times in 5 shots, B 2 times in 5 shots, and C 3 times in 4 shots. All of them fire one shot each simultaneously at the target.
What is the probability that-
1. Two shots hit
2. At least two shots hit
Sol.
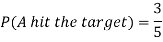
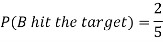
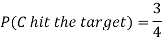
1. Now probability that 2 shots hit the target-
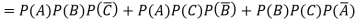
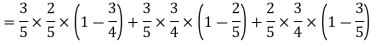
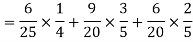
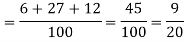
2.
Probability of at least two shots hitting the target
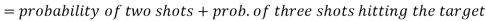
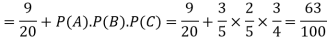
Theorems on Probability
Let A and B be two events of a sample space Sand let 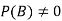 . Then the conditional probability of the event A, given B, denoted by
. Then the conditional probability of the event A, given B, denoted by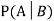 is defined by –
is defined by –
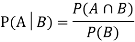
Theorem: If the events AandBdefined on a sample space S of a random experiment are independent, then
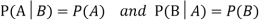
Example:A factory has two machines A and B making 60% and 40% respectively of the total production. Machine A produces 3% defective items, and B produces 5% defective items. Find the probability that a given defective part came from A.
SOLUTION:We consider the following events:
A: Selected item comes from A.
B: Selected item comes from B.
D: Selected item is defective.
We are looking for a 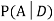 . We know:
. We know:
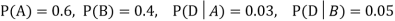
Now,
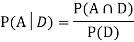
So we need
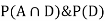
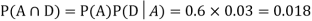
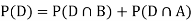
Since D is the union of the mutually exclusive events 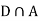 and
and 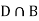 (the entire sample space is the union of the mutually exclusive events A and B)
(the entire sample space is the union of the mutually exclusive events A and B)
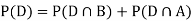
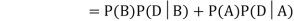
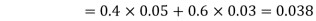
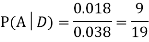
Example:Two fair dice are rolled, 1 red, and 1 blue. The Sample Space is
S = {(1, 1),(1, 2), . . . ,(1, 6), . . . ,(6, 6)}.Total -36 outcomes, all equally likely (here (2, 3) denotes the outcome where the red die show 2 and the blue one shows 3).
(a)Consider the following events:
A: Red die shows 6.
B: Blue die shows 6.
Find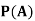 ,
, 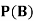 and
and 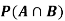 .
.
Solution: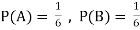
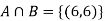
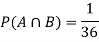
NOTE: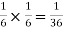 so
so 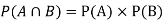 for this example. This is not surprising - we expect A to occur in
for this example. This is not surprising - we expect A to occur in  of cases. In
of cases. In  of these cases i.e. in
of these cases i.e. in 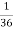 of all cases, we expect B to also occur.
of all cases, we expect B to also occur.
(b) Consider the following events:
C: Total Score is 10.
D: Red die shows an even number.
Find 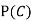 ,
, 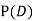 and
and 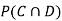 .
.
Solution: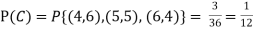
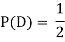
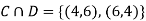
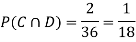
NOTE: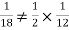 so,
so,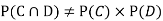 .
.
Why does multiplication not apply here as in part (a)?
ANSWER: Suppose C occurs: so the outcome is either (4, 6), (5, 5), or (6, 4). In two of these cases, namely (4, 6) and (6, 4), the event D also occurs. Thus
Although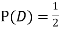 , the probability that D occurs given that C occurs is
, the probability that D occurs given that C occurs is  .
.
We write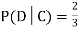 , and call
, and call 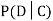 the conditional probability of D given C.
the conditional probability of D given C.
NOTE: In the above example
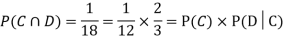
Example: Three urns contain 6 red, 4 black; 4 red, 6 black; 5 red, 5 black balls respectively. One of the urns is selected at random and a ball is drawn from it. If the ball is drawn is red find the probability that it is drawn from the first urn.
Solution:
 :The ball is drawn from urnI.
:The ball is drawn from urnI.
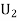 : The ball is drawn from urnII.
: The ball is drawn from urnII.
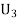 : The ball is drawn from urnIII.
: The ball is drawn from urnIII.
R:The ball is red.
We have to find 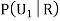
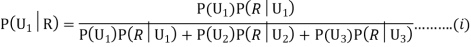
Since the three urns are equally likely to be selected
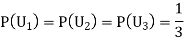
Also,
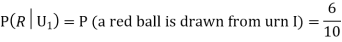
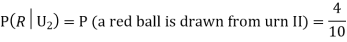
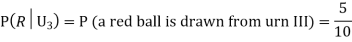
From (i), we have
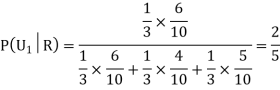
Key takeaways-
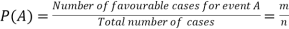
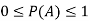
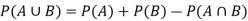
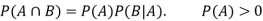
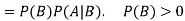
5. 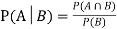
Let S be a sample space and 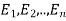 be n mutually exclusive events with P(
be n mutually exclusive events with P(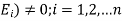 .
.
Let A be an event which is a sub-set of 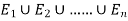 with P(A)>0, then-
with P(A)>0, then-
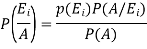
Where i = 1, 2, ……. ,n
And 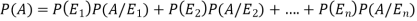 [which is the law of total probability]
[which is the law of total probability]
Example- Three urn contains 6 red, 4 black; 4 red, 6 black; 5 red, 5 black balls respectively. One of the urn is selected randomly and a ball is drawn from it.
If the ball drawn is red then find the probability that it is drawn from the first urn.
Sol.
Let,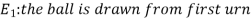
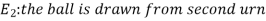
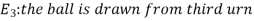
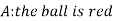
Now we have to find- 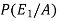
By using Bayes theorem-
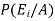 =
= 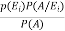
Here three urns equally likely to be selected-
So that-
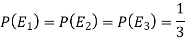
And-
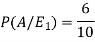
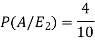
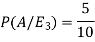
So that-
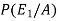 =
= 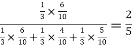
Hence the required probability is 2/5.
Example: A person speaks the truth 3 out of 4 times. A die is thrown. She reports that there are five. What is the chance there is 5?
Sol.
Let 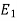 be the event that the person speaksthe truth,
be the event that the person speaksthe truth, 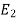 be the event that she tells lie and A be the event that she reports a five.
be the event that she tells lie and A be the event that she reports a five.
So that-
By the law of total probability-
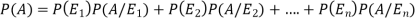
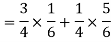
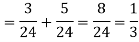
Now we have to find- 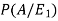
By using Bayes theorem-
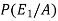 =
= 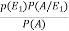
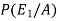 =
= 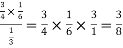
Which is the required probability.
Example: ln a bolt factory machines 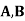 and
and 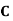 manufacturerespectively 25%, 35% and 40% of the total. lf their output 5, 4, and 2 percent are defective bolts. A bolt is drawn at random from theproduct and is found to be defective. What is the probability that it was manufactured by machine B.?
manufacturerespectively 25%, 35% and 40% of the total. lf their output 5, 4, and 2 percent are defective bolts. A bolt is drawn at random from theproduct and is found to be defective. What is the probability that it was manufactured by machine B.?
Solution: bolt is manufactured by machine 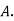
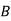 : bolt is manufactured by machine
: bolt is manufactured by machine 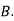
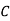 : bolt is manufactured by machine
: bolt is manufactured by machine 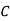
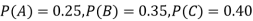
The probability of drawing a defective bolt manufactured by machine 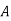 is
is 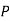 (D/A)
(D/A) 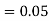
Similarly, 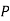 (D/B)
(D/B) 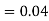 and
and 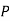 (D/C)
(D/C) 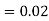
By Baye’s theorem
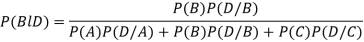
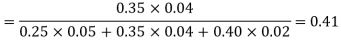
Key takeaways-
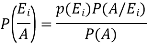
A random variable is a real-valued function whose domain is a set of possible outcomes of a random experiment and range is a subset of the set of real numbers and has the following properties:
i) Each particular value of the random variable can be assigned some probability
ii) Uniting all the probabilities associated with all the different values of the random variable gives the value 1.
A random variable is denoted by X, Y, Z, etc.
For example, if a random experiment E consists of tossing a pair of dice, the sum X of the two numbers which turn up have the value 2,3,4,…12 depending on chance. Then X is a random variable
Discrete random variable-
A random variable is said to be discrete if it has either a finite or a countable number of values. A countable number of values means the values which can be arranged in a sequence.
Note- if a random variable takes a finite set of values it is called discrete and if a random variable takes an infinite number of uncountable values it is called a continuous variable.
By definition, a random variable X and its distribution are discrete if X assumes only finitely many or at most countably many values 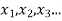 called the possible values of X. with positive probabilities
called the possible values of X. with positive probabilities 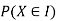 is zero for any interval J containing no possible values.
is zero for any interval J containing no possible values.
The discrete distribution of X is also determined by the probability functions f (x) of X, defined by
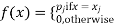
From this, we get the values of the distribution function F (x) by taking sums.
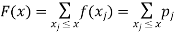
Example: 1. No. of head obtained when two coins are tossed.
2. No. of defective items in a lot.
Discrete probability distributions-
Let X be a discrete variate which is the outcome of some experiments. If the probability that X takes the values of x is 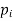 , then-
, then-
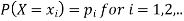
Where-
1. 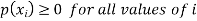
2. 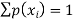
The set of values 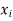 with their probabilities
with their probabilities 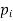 makes a discrete probability distribution of the discrete random variable X.
makes a discrete probability distribution of the discrete random variable X.
The probability distribution of a random variable X can be exhibited as follows-
X | 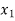 | 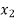 | 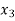 |
P(x) | 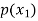 | 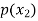 | 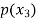 |
Example: Find the probability distribution of the number of heads when three coins are tossed simultaneously.
Sol.
Let be the number of heads in the toss of three coints
The sample space will be-
{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
Here variable X can take the values 0, 1, 2, 3 with the following probabilities-
P[X= 0] = P[TTT] = 1/8
P[X = 1] = P [HTT, THH, TTH] = 3/8
P[X = 2] = P[HHT, HTH, THH] = 3/8
P[X = 3] = P[HHH] = 1/8
Hence the probability distribution of X will be-
X | 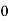 | 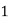 | 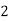 | 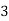 |
P(x) |  |  |  |  |
Example: For the following probability distribution of a discrete random variable X,

Find-
1. The value of c.
2. P[1<x<4]
Sol,
1. We know that-
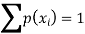
So that-
0 + c + c + 2c + 3c + c = 1
8c = 1
Then c = 1/8
Now, 2. P[1<x<4] = P[X = 2] + P[X = 3] = c + 2c = 3c = 3× 1/8 = 3/8
Let a random variable X has a probability distribution which assumes the values say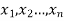 with their associated probabilities
with their associated probabilities 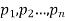 then the mathematical expectation can be defined as-
then the mathematical expectation can be defined as-
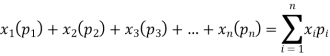
The expected value of a random variable X is written as E(X).
The expected value for a continuous random variable is
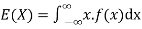
Example: If a random variable X has the following probability distribution in the tabular form then what will be the expected value of X.
X | 0 | 1 | 2 |
P(x) | 1/4 | 1/2 | 1/4 |
Sol.
We know that-
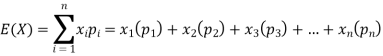
So that-
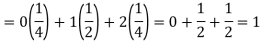
Example: Find the expectations of the number of an unbiased die when thrown.
Sol. Let X be a random variable that represents the number on a die when thrown.
X can take the values-
1, 2, 3, 4, 5, 6
With
P[X = 1] = P[X = 2] = P[X = 3] = P[X = 4] = P[X = 5] = P[X = 6] = 1/6
The distribution table will be-
X | 1 | 2 | 3 | 4 | 5 | 6 |
p(x) | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Hence the expectation of number on the die thrown is-
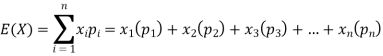
So that-
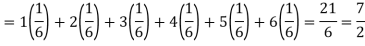
Example. In a lottery, m tickets are drawn at a time out of a ticket numbered from 1 to n. Find the expected value of the sum of the numbers on the tickets drawn.
Solution. Let 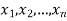 be the variables representing the numbers on the first, second,…nth ticket. The probability of drawing a ticket out of n ticket spelling in each case 1/n, we have
be the variables representing the numbers on the first, second,…nth ticket. The probability of drawing a ticket out of n ticket spelling in each case 1/n, we have
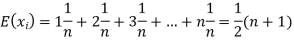
Therefore the expected value of the sum of the numbers on the tickets drawn
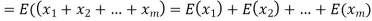
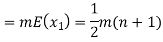
A random variable whose value cannot be arranged in a sequence is called a continuous random variable.
A continuous random variable is represented by a different representation, called the probability density function.
Probability density function-
Suppose f( x ) be a continuous function of x. Suppose the shaded region ABCDshown in the following figure represents the area bounded by y = f( x ), the x-axis and the ordinates at the points x and x + δx, where δxis the length of the interval ( x, x + δx ).ifδx is very-very small, then the curve AB will act as a line and hence the shaded region will be a rectangle whose area will be AD × DCthis area = probability that X lies in the interval ( x, x +δx )
= P[ x≤ X ≤ x +δx ]
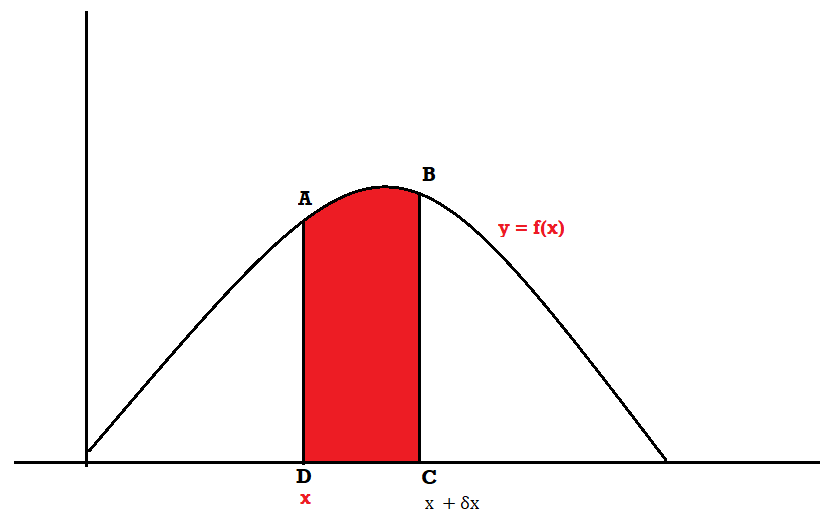
Hence,
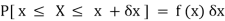
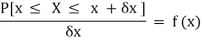
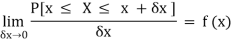
Properties of Probability density function-
1. 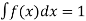
2. 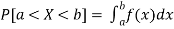
Example: If a continuous random variable X has the following probability density function:
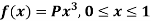
Then find-
1. P[0.2 < X < 0.5]
Sol.
Here f(x) is the probability density function, then-
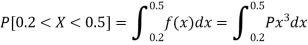
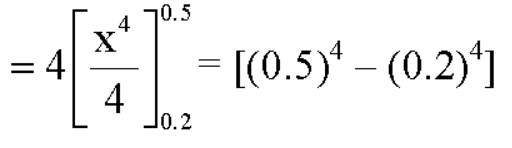
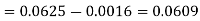
Example. The probability density function of a variable X is
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
P(X) | k | 3k | 5k | 7k | 9k | 11k | 13k |
(i) Find 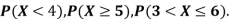
(ii) What will be e minimum value of k so that 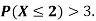
Solution. (i) If X is a random variable then
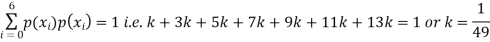
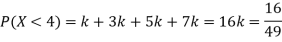
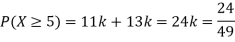
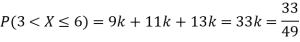
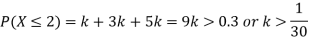
(ii)Thus minimum value of k=1/30.
Example. A random variate X has the following probability function
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
P (x) | 0 | K | 2k | 2k | 3k | 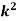 | 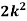 | 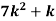 |
(i) Find the value of the k.
(ii) 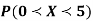
Solution. (i) If X is a random variable then
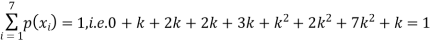
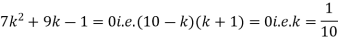
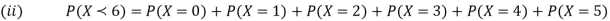
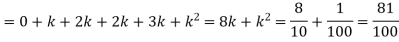
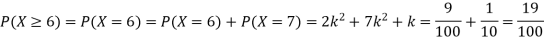
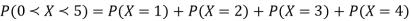
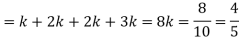
Distribution functions and densities
A function F defined for all values of a random variable X by
F( x ) = P[X ≤ x ] is called the distribution function. It is also known as the cumulative distribution function (c.d.f.) of X since it is the cumulative probability of X up to and including the value x.
Continuous Distribution Function
The distribution function of a continuous random variable is called the continuous distribution function or cumulative distribution function (c.d.f.).
Let X be a continuous random variable having the probability density function
f( x ), as defined in the last section of this unit, then the distribution function
F( x ) is given by
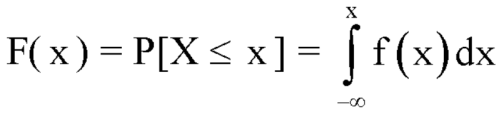
Example: The pdf of a continuous random variable is given below-
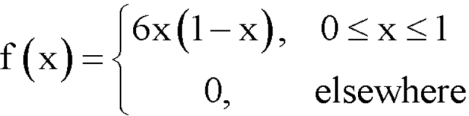
Then find the c.d.f. of X.
Sol.
The c.d.f. of X will be given by-
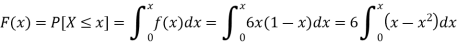
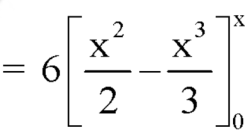
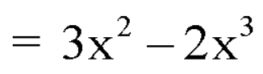
Hence the c.d.f will be-
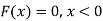
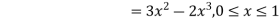
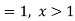
A probability distribution is an arithmetical function that defines completely possible values &possibilities that a random variable can take in a given range. This range will be bounded between the minimum and maximum possible values. But exactly where the possible value is possible to be plotted on the probability distribution depends on some influences. These factors include the distribution's mean, SD, Skewness, and kurtosis.
Binomial Distribution:
Binomial Distribution 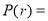
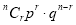
To find the probability of the happening of an event once, twice, …., r times… exactly in n trials.
Let the probability of the happening of an event A in one trial be 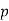 and its probability of not happening be
and its probability of not happening be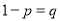
We assume that there are n trials and the happening of the event 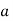 is
is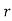 times and it’s not happening n-r times.
times and it’s not happening n-r times.
This may be shown as follows
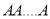
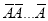
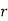 times
times 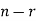 times ….(1)
times ….(1)
A indicates it's happening, 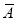 its failure,and
its failure,and 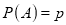
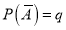 .
.
We see that (1) has the probability
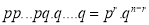 …. (2)
…. (2)
r times n-r times
Clearly (1) is merely one order of arranging r A’s
The probability of (1)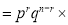 Number of different arrangements of
Number of different arrangements of 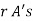 and
and 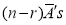 .
.
The number of different arrangements of 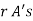 and
and 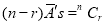
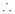 Probability off the happening of an event
Probability off the happening of an event 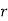 times
times 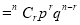
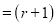 th term of
th term of 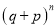
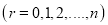
If 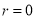 , probability of happening of an event 0 times
, probability of happening of an event 0 times 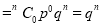
If  , probability of happening of an event 1 time
, probability of happening of an event 1 time 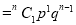
If  , probability of happening of an event 2 times
, probability of happening of an event 2 times 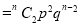
If 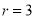 , probability of happening of an event 3 times
, probability of happening of an event 3 times 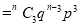
These terms are the successive terms in the expansion of 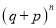 . Hence it is called Binomial distribution.
. Hence it is called Binomial distribution.
Example
If on average one ship in every ten is wrecked, find the probability that of 5 ships expected to arrive, 4 at least will arrive safely.
Solution:
Out of 10 ships, one ship is wrecked.
i.e., Nine ships out of ten ships are safe. P(safety)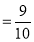
P(At least 4 ships out of 5 ships are safe)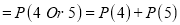
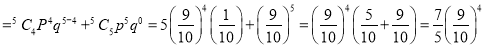
Example
The overall percentage of failures in a certain examination is 20. If six candidates appear in the examination, what is the probability that at least five pass the examination?
Solution:
Probability of failures 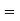
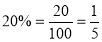
Probability 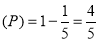
Probability of at least five passes 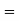 P(5 or 6)
P(5 or 6)
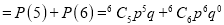
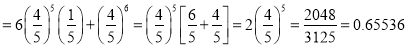
Example
The probability that a managed 60 will live to be 70 is 0.65. What is the probability that out of 10 items, now 60, at least 7 will live to be 70?
Solution
The probability that a man aged 60 will live to be 70
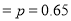
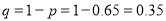
Number of men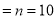
The probability that at least 7 men will live to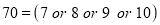
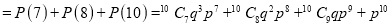
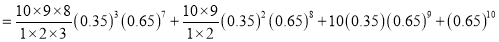
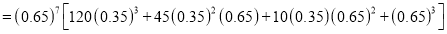
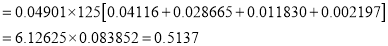
Example
A die is thrown 8 times and it is required to find the probability that 3 will show (i) Exactly 2 times
(ii) At least seven times (iii) At least once.
Solution:
The probability of throwing 3 in a single trial =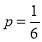
The probability of not throwing 3 in a single trial 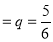
(i) P (getting 3 exactly 2 times)=P (getting 3, at 7 or 8 times) 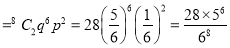
(ii) P (getting 3, at least seven times)=P (getting 3, at 7 or 8 times) 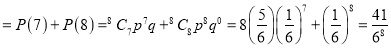
(iii) P (getting 3 at least once)
=P (getting 4, at 1 or 2 or 3 or 4 or 5 or 6 or 7 or 8 times)
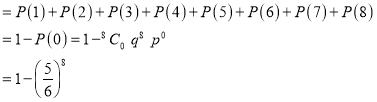
Example:
Assuming that 20% of the population of a city are literate, so that the chance of an individual being literate is 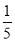 and assuming that 100 investigators each take 10 individuals to see whether they are literate, how many investigators would you expect 3 or less were literate.
and assuming that 100 investigators each take 10 individuals to see whether they are literate, how many investigators would you expect 3 or less were literate.
Solution 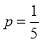
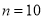
P (3 or less) = P (0 or 1 or 2 or 3 )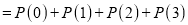
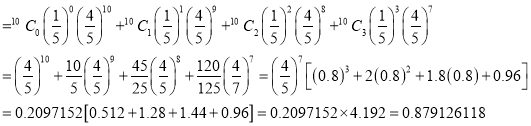
Required number of investigators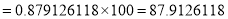
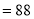 approximately
approximately
Mean of Binomial Distribution
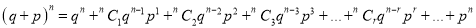
Successes 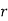 | Frequency 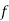 | 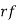 |
0 | 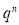 |
|
1 | 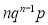 | 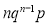 |
2 | 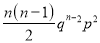 | 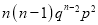 |
3 | 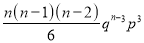 | 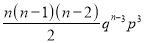 |
… | …. | …. |
4 | 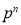 | 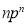 |
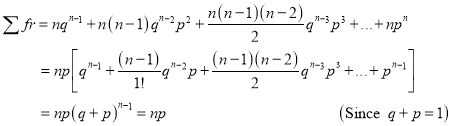
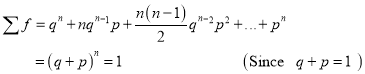
Hence Mean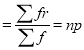
Standard Deviation of Binomial Distribution
Successes 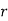 | Frequency 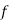 | 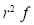 |
0 | 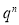 | 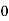 |
1 | 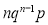 | 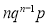 |
2 | 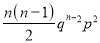 | 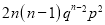 |
3 | 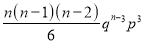 | 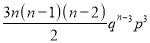 |
…. | …. | … |
n | 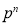 | 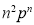 |
We know that 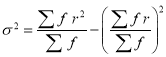 ….(1)
….(1)
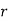 is the deviation of items (successes) from 0.
is the deviation of items (successes) from 0.
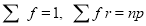
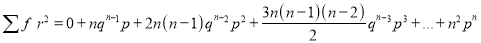
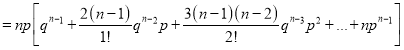
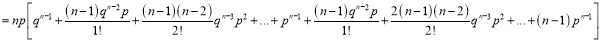
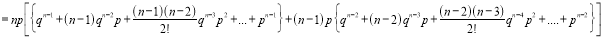
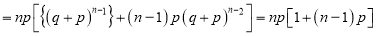
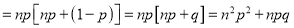
Putting these values in (1), we have
Variance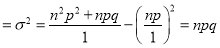
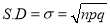
Hence for the binomial distribution, Mean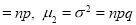
Example:
A die is tossed thrice. Success is getting 1 or 6 on a toss. Find the mean and variance of the number of successes.
Solution:
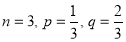
Mean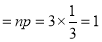
Variance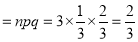
Recurrence relation for the binomial distribution
By Binomial distribution 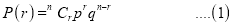
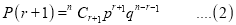
On dividing (2) by (1), we get
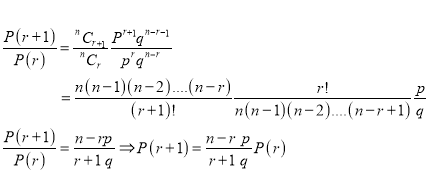
Poisson Distribution:
Poisson distribution is a particular limiting form of the Binomial distribution when p or (q) is very small and n is large enough.
Poisson distribution is 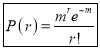
Where m is the mean of the distribution.
Proof:
In Binomial distribution
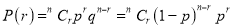 { Since mean
{ Since mean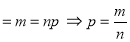 }
}
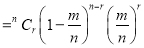 (
(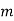 is constant)
is constant)
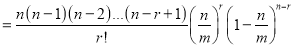
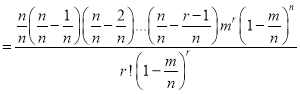
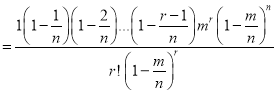
Taking limits, when n tends to infinity
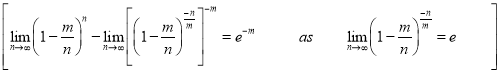
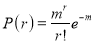
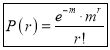
Mean of Poisson Distribution
Successes  | Frequency  | 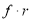 |
0 | 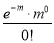 | 0 |
1 | 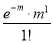 | 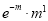 |
2 | 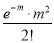 | 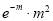 |
3 | 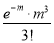 | 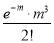 |
… | … | …. |
r | 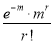 | 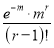 |
… | … | …. |
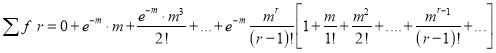
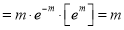
Mean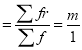
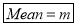
Standard Deviation of Poisson Distribution
Successes 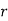 | Frequency 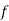 | Product 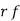 | Product 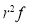 |
0 | 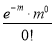 | 0
| 0 |
1 | 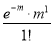 | 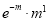 | 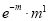 |
2 | 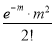 | 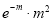
| 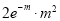 |
3 | 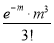 | 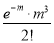 | 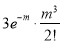 |
… | …. | …. | … |
r | 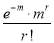 | 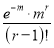 | 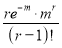 |
… | …. | … | … |
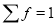
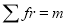
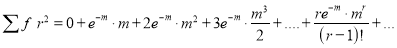
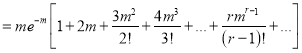
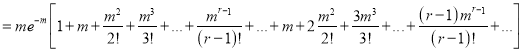
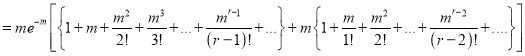
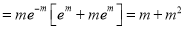
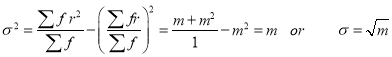
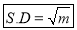
Hence mean and variance of a Poisson distribution are each equal to m. Similarly, we can obtain,
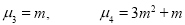
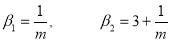
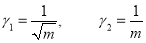
Mean Deviation:
Show that in a Poisson distribution with unit mean, and the mean deviation about the mean is 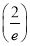 times the standard deviation.
times the standard deviation.
Solution: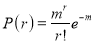 But mean=1 i.e.,
But mean=1 i.e., 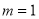 and
and 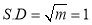
Hence, 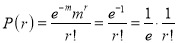
 |  |  | 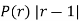 |
0 | 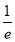 | 1 | 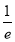 |
1 | 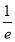 | 0 |
|
2 | 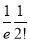 | 1 | 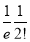 |
3 | 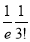 | 2 | 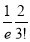 |
4 | 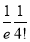 | 4 | 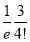 |
… | …. | …. | … |
r | 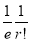 | r-1 | 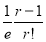 |
Mean Derivation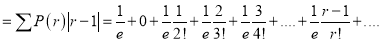
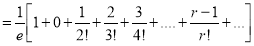
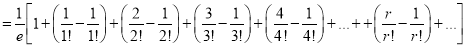
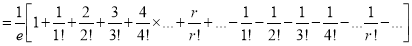
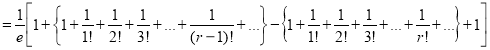
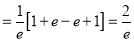
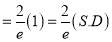
Moment Generating Function of Poisson Distribution
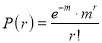
Solution:
Let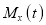 be the moment generating function, then
be the moment generating function, then
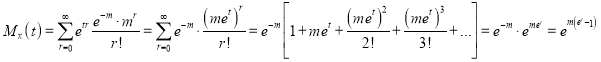
Cumulants
The cumulant generating function 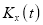 is given by
is given by
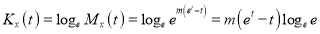
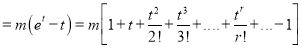
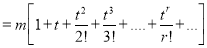
Now 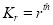 cumulant
cumulant Coefficient of
Coefficient of 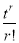 in K(t)
in K(t)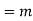
i.e., 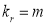 where
where 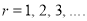
Mean 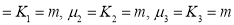
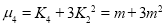
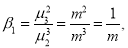
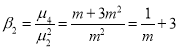
Recurrence formula for Poisson Distribution:
Solution: Poisson Distribution


On dividing (2) by (1) we get
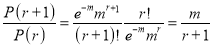
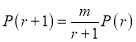
Example
Assume that the probability of an individual coal miner being killed in a mine accident during a year is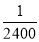 . Use appropriate statistical distribution to calculate the probability that in a mine employing 200 metres, there will be at least one fatal accident in a year.
. Use appropriate statistical distribution to calculate the probability that in a mine employing 200 metres, there will be at least one fatal accident in a year.
Solution:
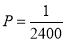 ,
, 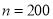
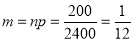
P(At least one)=P(1 or 2 or 3 or …. or 200)
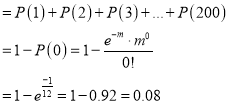
Example:
Suppose 3% of bolts made by a machine are defective, the defects occurring at random during production. If bolts are packaged 50 per box, find
(a) exact probability and
(b) Poisson approximation to it, that a given box will contain 5 defectives.
Solution:
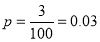
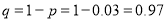
(a) Hence the probability for 5 defective bolts in a lot of 50
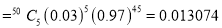 (Binomial Distribution)
(Binomial Distribution)
(b) To get Poisson approximation 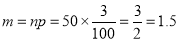
Required Poisson approximation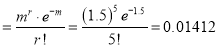
Example:
In a certain factory producing cycle tyres there is a small chance of 1 in 500 tyres to be defective. The tyres are supplied in lots of 10. Using Poisson distribution calculate the approximate number of lots containing no defective, one defective, and two defective tyres, respectively, in a consignment of 10000 lots.
Solution:
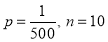
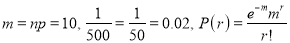
S.No | Probability of defective | Number of lots containing defective |
1 | 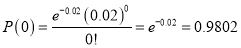 | 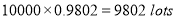
|
2 | 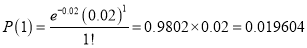 | 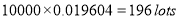
|
3 | 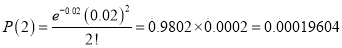 | 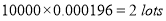
|
Normal Distribution:
The normal distribution is continuous. It is derived as the limiting form of the Binomial distribution for large values of n and p and q are not very small.
The Normal distribution is given by the equation
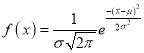 ….(1)
….(1)
Where 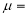 mean,
mean, 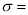 standard deviation,
standard deviation,  ,
, 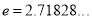
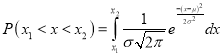
On substitution 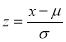 in (1), we get
in (1), we get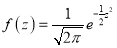 ….(2)
….(2)
Here mean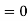 , standard deviation
, standard deviation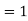
(2) is known as the standard form of normal distribution.
Mean for Normal Distribution:
Mean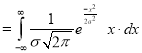 [Putting
[Putting 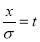 ]
]
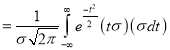
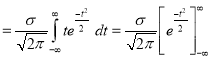
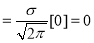
Standard Deviation for Normal Distribution:
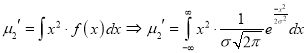
Put 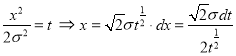
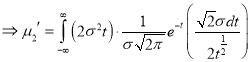
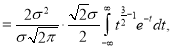
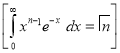
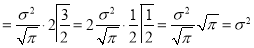
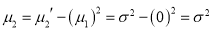
Median of the Normal Distribution
If a is the median, then it divides the total area into two halves so that,
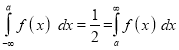
Where 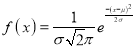
Suppose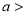 mean,
mean, 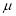 then
then
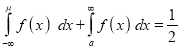 [But
[But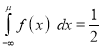 ]
]
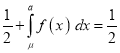 (
(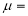 mean)
mean)
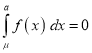
Thus 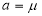
Similarly, when 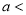 mean, we have
mean, we have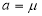
Thus, median=median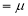 .
.
Mean Deviation about the Mean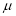
Mean Deviation 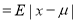
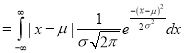
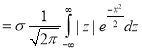 where
where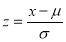
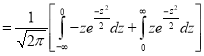
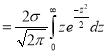 (as the function is given)
(as the function is given)
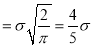 approximately.
approximately.
Mode of the Normal distribution
We know that mode is the value of the variate x for which 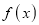 is maximum. Thus, differential calculus
is maximum. Thus, differential calculus 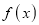 is maximum if
is maximum if 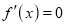 and
and 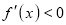
Where 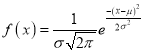
Clearly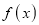 will be maximum when the exponent will bemaximum which will be the when
will be maximum when the exponent will bemaximum which will be the when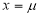
Thus mode is 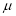 and modal ordinate
and modal ordinate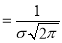
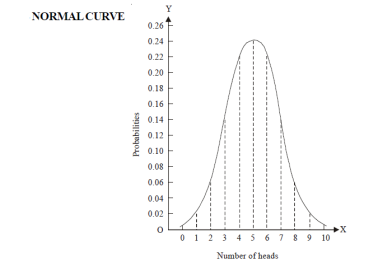
Let us show binomial distribution graphically. The probabilities of heads in 1 toss are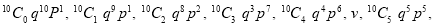
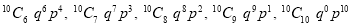 .
.
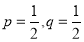 . It is shown in the given figure.
. It is shown in the given figure.
If the variates (heads here) are treated as if they were continuous, the required probability curve will be normal as shown in the above figure by dotted lines.
Properties of the normal curve: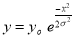
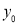
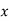
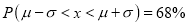
(b) 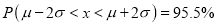
(c) 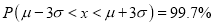
Hence (a) About 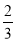 of the values will lie between
of the values will lie between 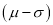 and
and 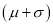 .
.
(b) About 95% of the values will lie between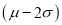 and
and 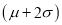 .
.
(c) About 99.7% of the values will lie between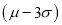 and
and 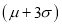 .
.
The area under the Normal curve
By taking 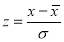 , the standard normal curve is formed.
, the standard normal curve is formed.
The total area under this curve is 1. The area under the curve is divided into two equal parts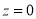 . The left-hand side is and right-hand side area too
. The left-hand side is and right-hand side area too 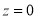 is
is 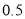 . The area between the ordinate
. The area between the ordinate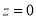 .
.
Example
On final examination in mathematics, the mean was 72, and the standard deviation was 15. Determine the standard deviation scores of students receiving grades.
(a) 60 (b) 93 (c) 72
Solution:
(a) 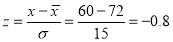 (b)
(b) 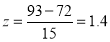 (c)
(c) 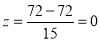
Example: Find the area under the normal curve in each of the cases.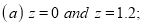
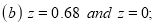
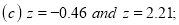
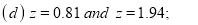
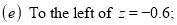
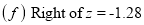
Solution:
(a) Area between 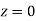 and
and 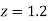 (b) Area between
(b) Area between 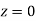 and
and 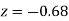
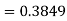
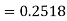
(c) Required area  (Area between
(Area between 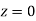 and
and 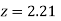 )+
)+
(Area between 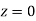 and
and 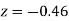 )
)
=(Area between 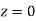 and
and 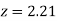 )
)
+(Area between 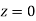 and
and 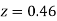 )
)
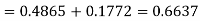
(d) Required area 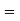 (Area between
(Area between 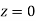 and
and 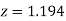 ) – (Area between
) – (Area between 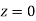 and
and 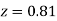 )
)
(e) Required area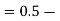 (Area between
(Area between 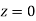 and
and 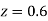 )
)
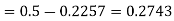
(f) Required area = (Area between 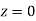 and
and 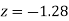 )
)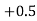
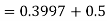
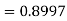
Example. The mean inside diameter of a sample of 200 washers produced by a machine is 0.0502 cm and the standard derivation is 0.005 cm. The purpose for which these washers are intended allows a maximum tolerance in the diameter of 0.496 to 0.508 cm, otherwise, the washers are considered defective. Determine the percentage of defective washers produced by the machine, assuming the diameters are normally distributed
Solution:
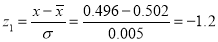
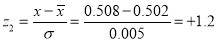
Area for non-defective washers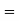 Area between
Area between 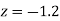 and
and 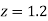
= 2 Area between 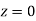 and
and 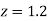
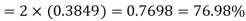
Percentage of defective washers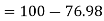
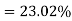
Example:
A manufacturer knows from experience that the resistance of resistors he produces is normal with mean 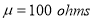 and standard deviation
and standard deviation 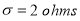 What percentage of resistors will have resistance between 98 ohms and 102 ohms?
What percentage of resistors will have resistance between 98 ohms and 102 ohms?
Solution:
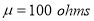
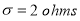
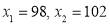
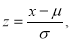
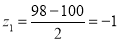
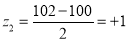
Area between 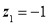 and
and 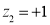
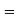 (Area between
(Area between 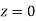 and
and 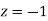 )+(Area between
)+(Area between 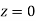 and
and 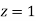 )
)
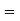 (Area between
(Area between 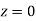 and
and 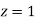 )=2
)=2 0.3413=0.6826
0.3413=0.6826
Percentage of resistors having resistance between 98 ohms and 102 ohms =68.26
Example
In a normal distribution, 31% of the items are under 45 and 8% are over 64. Find the mean and standard deviation of the distribution.
Solution:
Let 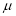 be the mean and
be the mean and 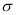 S.D.
S.D.
If 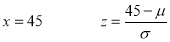
If 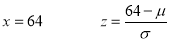
The area between 0 and 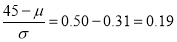
[From the table, for the area 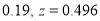 ]
]
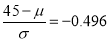 …(1)
…(1)
The area between 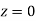 and
and 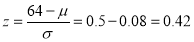
(From the table, for the area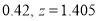 )
)
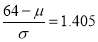 …(2)
…(2)
Solving (1) and (2), we get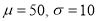
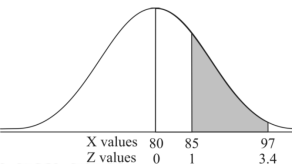
Example: If a random variable X is normally distributed with mean 80 and standard deviation 5, then find-
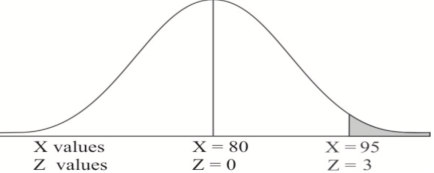
1. P[X > 95]
2. P[X < 72]
3. P [85 < X <97]
[Note- use the table- area under the normal curve]
Sol.
The standard normal variate is – 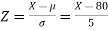
Now-
1. X = 95,
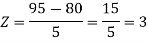
So that-
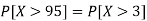
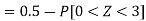
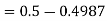
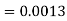
2. X = 72,
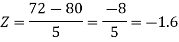
So that-
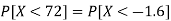
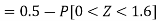
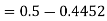
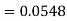
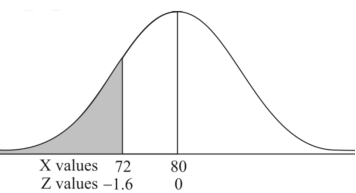
3. X = 85,
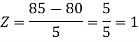
X = 97,
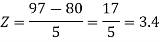
So that-
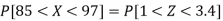
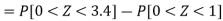
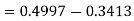
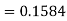
Example: In a company, the mean weight of 1000 employees is 60kg and the standard deviation is 16kg.
Find the number of employees having their weights-
1. Less than 55kg.
2. More than 70kg.
3. Between 45kg and 65kg.
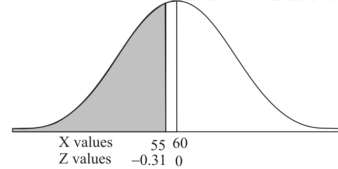
Sol. Suppose X be a normal variate = the weight of employees.
Here mean 60kg and S.D. = 16kg
X 
Then we know that-
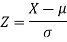
We get from the data,
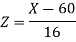
Now-
1. For X = 55,
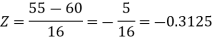
So that-
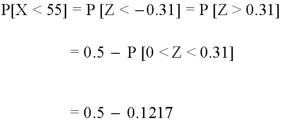
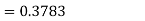
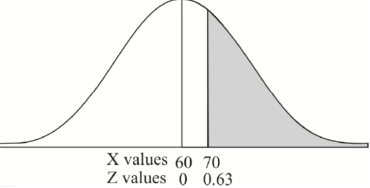
2. For X = 70,
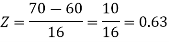
So that-
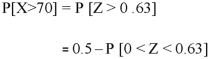
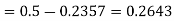
3. For X = 45,
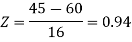
For X = 65,
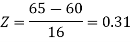
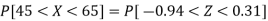
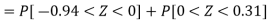
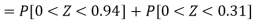
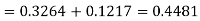
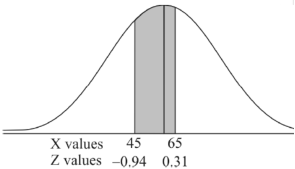
Hence the number of employees having weights between 45kg and 65kg-
Example: The life of electric bulbs is normally distributed with a mean of 8 months and a standard deviation of 2 months.
If 5000 electric bulbs are issued how many bulbs should be expected to need replacement after 12 months?
[Given that P (z ≥ 2) = 0. 0228]
Sol.
Here mean (μ) = 8 and standard deviation = 2
Number of bulbs = 5000
Total months (X) = 12
We know that-
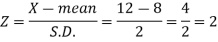
Area (z ≥ 2) = 0.0228
Number of electric bulbs whose life is more than 12 months ( Z> 12)
= 5000 × 0.0228 = 114
Therefore replacement after 12 months = 5000 – 114 = 4886 electric bulbs.
Hyper-geometric distribution-
Let a box contains ‘m’ white and ‘n’ black balls. If ‘r’ balls are drawn with replacement, then the probability that ‘k’ of them will be white is-
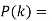
Where k = 0, 1, 2,..,r, 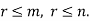
This distribution is known as Hypergeometric distribution.
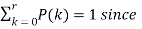
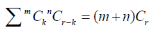
Key takeaways-
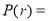
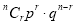
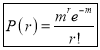
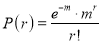
4. The Normal distribution is given by the equation
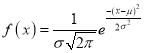
5. median=median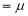 in case of normal distribution
in case of normal distribution
When a small number of elements are selected from a population is called a sample.
The process of drawing a sample is known as sampling.
When each member of the population has an equal chance of being selected in the sample is called random sampling.
Parameter-
A parameter is a function of population values which is used to represent the certain characteristic of the population. For example, population mean, population variance, population coefficient of variation, population correlation coefficient, etc. are all parameters
Statistic-
The quantity calculated from sample values and does not contain any unknown parameter is called a statistic.
“The process of getting the sample result for the whole population is known as statistical inference.”
Standard error-
The standard deviation of a sampling distribution of a statistic is known as standard error and it is denoted by SE.
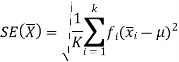
Note-
If 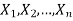 is a random sample of size n taken from a population with mean
is a random sample of size n taken from a population with mean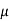 and variance
and variance 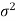
Then the standard error of sample mean is given by-
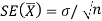
Test of hypothesis-
Based on the given information, we draw a certain conclusion about the population.
These conclusionsare made by some assumptions.
These assumptions are called a statistical hypothesis.
Null hypothesis-
The hypothesis which we test is known as the null hypothesis.
R.A. Fisher defined null hypothesis as-
“A null hypothesis is a hypothesis which is tested for possible rejection under the assumption that it is true”
The hypothesis against the null hypothesis is called the alternative hypothesis (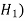 .
.
The null hypothesis is denoted by 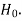
Two types of errors-
Decision | 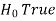 | 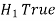 |
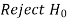 | 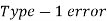 | 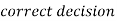 |
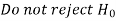 | 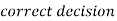 | 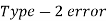 |
Type-I error-
If we reject the null hypothesis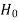 when it is true is called a type-I error. The probability of type-I error is called the size of the test, and it is denoted by α.
when it is true is called a type-I error. The probability of type-I error is called the size of the test, and it is denoted by α.
Type-II error-
If we do not reject the null hypothesis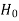 when it is false is called a type-I error.
when it is false is called a type-I error.
The probability of type-I error is denoted by β.
(1 – β) is the probability of correct decisions and it is known as the power of the test.
Level of significance-
The probability of type-I error is known as a level of significance of a test. It is also called the critical region and denoted by α.
It is pre-fixed as a 5% or 1% level of significance.
Note- the probability of the value of the variate falling in the critical region is the level of significance. If it falls in the critical region then the hypothesis is rejected.
One-tailed and two-tailed tests-
A test of testing the null hypothesis is said to be a two-tailed test if the alternative hypothesis is two-tailed whereas if the alternative hypothesis is one-tailed then a test of testing the null hypothesis is said to be a one-tailed test.

Confidence limits-
The 95% confidence limits are 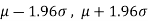 .
.
If a sample statistic lies between the intervals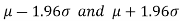 then we call it a 95% confidence interval.
then we call it a 95% confidence interval.
If a sample statistic lies between the intervals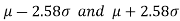 then we call it a 99% confidence interval.
then we call it a 99% confidence interval.
The numbers 1.96 and 2.58 are the confidence coefficients.
Test of significance of large samples-
For the normal distribution, 5% of the observations lie outside 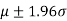 and only 1% lie outside
and only 1% lie outside 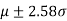
Note- Normal distribution is the limiting case of binomial distribution when the data points are large.
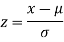
Here z is the standard normal variate.
We find the value of z.
Now the test of significance based on the value of z-
1. If |z|<1.96, the difference between the observed and expected number of successes is not significant at the 5% level of significance.
2. If |z|>1.96, the difference is significant at the 5% level of significance.
3. If |z|<2.58, the difference between the observed and expected number of successes is not significant at the 1% level of significance.
4. If |z|>2.58, the difference is significant at the 1% level of significance.
Formation of hypotheses-
Example: A company has replaced its original technology of producing electric bulbs with CFL technology. The company manager wants to compare the average life of bulbs manufactured by original technology and new technology CFL. Write appropriate null and alternate hypotheses
Sol.
Let the average life of original and CFL technology bulbs are denoted by 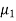 and
and 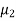 .
.
The null and alternative hypotheses will be-
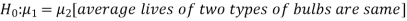

Here the alternate hypothesis is two-tailed so that the test will also be two-tailed.
If the manager is interested just to know whether the average life of CFL is greater than the original technology bulbs then the null and alternative hypotheses will be-
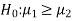
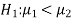
Here the alternative hypothesis is left tailed so that the corresponding test will also be left tailed.
Step by step method of testing a hypothesis-
Step-1 first setup the null and alternative hypothesis. Let we want to test the assumed value of 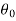 of parameter
of parameter 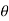 .
.
We can take the null and alternative hypothesis as-
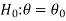
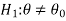
Or
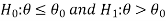
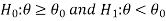
In the case of two populations-
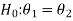
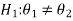
Or
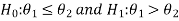
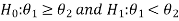
Step-2: Establish criteria for rejection or non-rejection of the null hypothesis, that is decide the level of significance at which we want to test our hypothesis. Generally, we take it as a 5% or 1% level of significance.
Step-3: Now choose the appropriate test statistic under  for testing the null hypothesis.
for testing the null hypothesis.
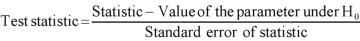
And that specifies the sampling distribution of the test statistic in the standard form Z, chi-square, t, and F.
Step-4: Calculate the value of test statistic as in step-3 based on observed sample observations.
Step-5: Get the critical value in the sampling distribution of the test statistic and make the rejection region of α.
Step-6: Now compare the calculated value of the test statistic with the critical value and find that it lies in the rejection or non-rejection region
Step-7: Now we come across two situations-
1. If the calculated value of the test statistic lies in the rejection region at the level of significance then we reject the null hypothesis.
That means the sample data provides us significant decision against the null hypothesis.
2. If the calculated value of the test statistic lies in the non-rejection region at the level of significance then we do not reject the null hypothesis. Its means that the sample data fails to provide us sufficient evidence against the null hypothesis.
Example: A manufacturer of electric bulbs claims that a certain pen manufactured by him has a mean life of at least 460 days. A purchasing officer selects a sample of 100 bulbs and put them on the test. The mean life of the sample found 453 days with a standard deviation of 25 days. Should the purchasing officer reject the manufacturer’s claim at a 1% level of significance?
Sol.
Here the population mean = 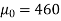
Sample size = n = 100
Sample mean = 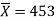
Sample standard deviation = S = 25
The null and alternative hypotheses will be-
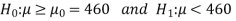
Here alternative hypothesis is left tailed so that the test is left tailed test-
Here population standard deviation is unknown so that we should use a t-test if the life of the bulbs follows a normal distribution.
But it is not the case. Here sample size is 100 which is large.
Note- a sample size of more than 30 is considered a large sample.
So here we use Z-test-
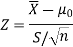
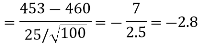
The critical value of Z statistic at a 1% level of significance is = -2.33
Since the calculated value of the test statistic is less than the critical value that means the test statistic lies in the rejection region.
Therefore we reject the null hypothesis.
So that we reject the manufacturer’s claim at a 1% level of significance.
Chi-square test-
The chi-square test works under the following circumstances-
1. When the given data is normally distributed.
2. Sample observations are random and independent.
When a fair coin is tossed 80 times we expect from the theoretical considerations that heads will appear 40 times and tail 40 times. But this never happens in practice that is the results obtained in an experiment do not agree exactly with the theoretical results. The magnitude of discrepancy between observations and theory is given by the quantity 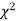 (pronounced as chi-squares). If
(pronounced as chi-squares). If 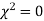 the observed and theoretical frequencies completely agree. As the value of
the observed and theoretical frequencies completely agree. As the value of 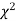 increases, the discrepancy between the observed and theoretical frequencies increases.
increases, the discrepancy between the observed and theoretical frequencies increases.
(1) Definition. If 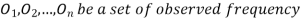 and
and 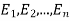 be the corresponding set of expected (theoretical) frequencies, then
be the corresponding set of expected (theoretical) frequencies, then 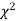 is defined by the relation
is defined by the relation
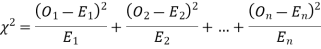
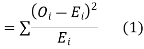
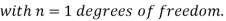
(2) Chi-square distribution
If 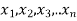 be n independent normal variates with mean zero and s.d. unity, then it can be shown that
be n independent normal variates with mean zero and s.d. unity, then it can be shown that 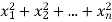 is a random variate having
is a random variate having 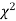 distribution with ndf.
distribution with ndf.
The equation of the 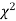 curve is
curve is
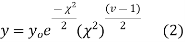
(3) Properties of 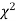 distribution
distribution
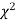
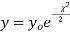
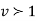
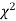
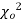
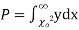
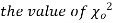 have been tabulated for various values of P and for values of v from 1 to 30. (Table V Appendix 2)
have been tabulated for various values of P and for values of v from 1 to 30. (Table V Appendix 2)
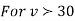 ,the
,the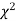 curve approximates to the normal curve and we should refer to normal distribution tables for significant values of
curve approximates to the normal curve and we should refer to normal distribution tables for significant values of 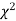 .
.
IV. Since the equation of 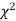 the curve does not involve any parameters of the population, this distribution does not dependent on the form of the population.
the curve does not involve any parameters of the population, this distribution does not dependent on the form of the population.
V. Mean = 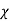 and variance =
and variance = 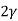
Goodness of fit
The values of 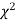 is used to test whether the deviations of the observed frequencies from the expected frequencies are significant or not. It is also used to test how well a set of observations fit given distribution
is used to test whether the deviations of the observed frequencies from the expected frequencies are significant or not. It is also used to test how well a set of observations fit given distribution 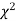 therefore provides a test of goodness of fit and may be used to examine the validity of some hypothesis about an observed frequency distribution. As a test of goodness of fit, it can be used to study the correspondence between theory and fact.
therefore provides a test of goodness of fit and may be used to examine the validity of some hypothesis about an observed frequency distribution. As a test of goodness of fit, it can be used to study the correspondence between theory and fact.
This is a nonparametric distribution-free test since in this we make no assumptions about the distribution of the parent population.
Procedure to test significance and goodness of fit
(i) Set up a null hypothesis and calculate
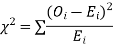
(ii) Find the df and read the corresponding values of 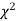 at a prescribed significance level from table V.
at a prescribed significance level from table V.
(iii) From 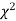 table, we can also find the probability P corresponding to the calculated values of
table, we can also find the probability P corresponding to the calculated values of 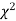 for the given d.f.
for the given d.f.
(iv) If P<0.05, the observed value of 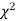 is significant at a 5% level of significance
is significant at a 5% level of significance
If P<0.01 the value is significant at the 1% level.
If P>0.05, it is good faith and the value is not significant.
Example. A set of five similar coins is tossed 320 times and the result is
Number of heads | 0 | 1 | 2 | 3 | 4 | 5 |
Frequency | 6 | 27 | 72 | 112 | 71 | 32 |
Solution. For v = 5, we have 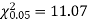
P, probability of getting a head=1/2;q, probability of getting a tail=1/2.
Hence the theoretical frequencies of getting 0,1,2,3,4,5 heads are the successive terms of the binomial expansion 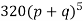
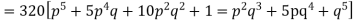
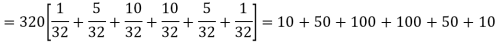
Thus the theoretical frequencies are 10, 50, 100, 100, 50, 10.
Hence, 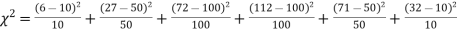
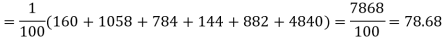
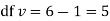
Since the calculated value of 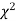 is much greater than
is much greater than 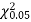 the hypothesis that the data follow the binomial law is rejected.
the hypothesis that the data follow the binomial law is rejected.
Example. Fit a Poisson distribution to the following data and test for its goodness of fit at a level of significance 0.05.
X | 0 | 1 | 2 | 3 | 4 |
F | 419 | 352 | 154 | 56 | 19 |
Solution. Mean m =
Hence, the theoretical frequency is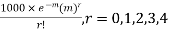
X | 0 | 1 | 2 | 3 | 4 | Total |
F | 404.9 (406.2) | 366 | 165.4 | 49.8 | 11..3 (12.6) | 997.4 |
Hence, 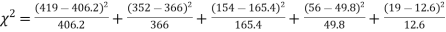
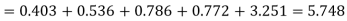
Since the mean of the theoretical distribution has been estimated from the given data and the totals have been made to agree, there are two constraints so that the number of degrees of freedom v = 5- 2=3
For v = 3, we have 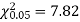
Since the calculated value of 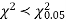 the agreement between the fact and theory is good and hence the Poisson distribution can be fitted to the data.
the agreement between the fact and theory is good and hence the Poisson distribution can be fitted to the data.
Example.In experiments of pea breeding, the following frequencies of seeds were obtained
Round and yellow | Wrinkled and yellow | Round and green | Wrinkled and green | Total |
316 | 101 | 108 | 32 | 556 |
Theory predicts that the frequencies should be in proportions 9:3:3:1. Examine the correspondence between theory and experiment.
Solution. The corresponding frequencies are
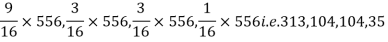
Hence, 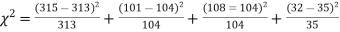
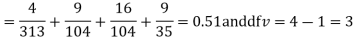
For v = 3, we have 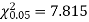
Since the calculated value of 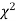 is much less than
is much less than 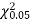 there is a very high degree of agreement between theory and experiment.
there is a very high degree of agreement between theory and experiment.
Significance test of a sample mean
Given a random small sample 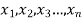 from a normal population, we have to test the hypothesis that the means of the population is μ. For this we first calculate
from a normal population, we have to test the hypothesis that the means of the population is μ. For this we first calculate 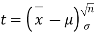
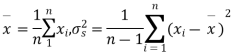
Then find the value of P for the given df from the table.
If the calculated value of 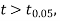 the difference between
the difference between 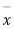 and μ is said to be significant at a 5% level of significance.
and μ is said to be significant at a 5% level of significance.
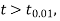 the difference is said to be significant at a 1% level of significance.
the difference is said to be significant at a 1% level of significance.
If 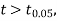 the data is said to be consistent with the hypothesis that μ is the mean of the population.
the data is said to be consistent with the hypothesis that μ is the mean of the population.
Example. A certain stimulus administered to each of 12 patients resulted in the following increases in blood pressure: 5, 2, 8, -1, 3, 0, -2, 1, 5, 0, 4, 6. Can it be concluded that the stimulus will in general be accompanied by an increase in blood pressure?
Solution. Let us assume that the stimulus administered to all 12 patients will increase the blood pressure. Taking the population to be normal with mean μ = 0 and S.D. 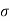
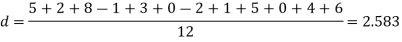
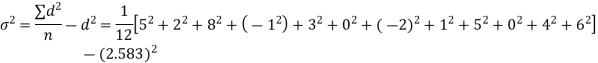
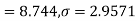
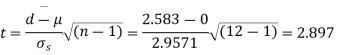
Here 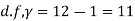
For 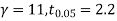 , from table IV.
, from table IV.
Since the 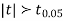 our assumptions are rejected i.e. the stimulus does not increase the B.P.
our assumptions are rejected i.e. the stimulus does not increase the B.P.
Example. The 9 items of a sample have the following values: 45, 47, 50, 52, 48, 47, 49, 53, 51. Does the mean of these differ significantly from the assumed mean of 47.5?
Solution. We find the mean and the standard deviation of the sample as follows
X | 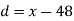 | 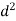 |
45 | -3 | 9 |
47 | -1 | 1 |
50 | 2 | 4 |
52 | 2 | 4 |
48 | 0 | 0 |
47 | -1 | 1 |
49 | 1 | 1 |
53 | 5 | 25 |
51 | 3 | 9 |
Total | 10 | 66 |
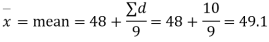
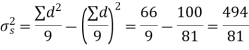
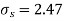
Hence, 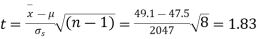
Here, 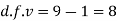
For v = 8, we get from table IV 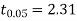
As the calculated value of 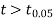 the value of t is not significant at a 5% level of significance which implies that there is no significant difference between
the value of t is not significant at a 5% level of significance which implies that there is no significant difference between 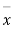 and μ. Thus the test provides no evidence against the population mean is 47.5.
and μ. Thus the test provides no evidence against the population mean is 47.5.
Example. A mechanism is making engine parts with an axle diameter of 0.7 inches. A random sample of 10 parts shows a means diameter of 0.742 inches with a standard deviation of 0.04 inches. Based on this sample would you say that the work is inferior?
Solution. Here we have,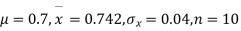
Taking the hypothesis that the product is not inferior that is there is no significant difference between 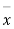 and μ.
and μ.
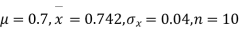
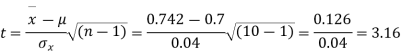
Degree of freedom 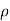 = 10-1=9
= 10-1=9
For 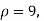 we get from table IV,
we get from table IV, 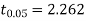
As the calculated value of 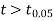 the value of t is significant at a 5% level of significance. This implies that
the value of t is significant at a 5% level of significance. This implies that 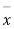 differs significantly from μ and the hypothesis is rejected. Hence the work is inferior. The work is inferior even at a 2% level of significance.
differs significantly from μ and the hypothesis is rejected. Hence the work is inferior. The work is inferior even at a 2% level of significance.
Comparison of large samples
Two large samples of sizes 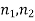 are taken from two populations giving proportions of attributes A's are
are taken from two populations giving proportions of attributes A's are 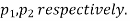
(a) On the hypothesis that the populations are similar as regards attribute A, we combine the two samples to find an estimate of the common value of the proportion of A’s in the populations which is given by
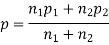
If 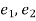 be the standard errors in the two samples then
be the standard errors in the two samples then
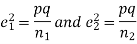
If e with the standard error of the difference between 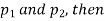
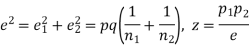
If z>3, the difference between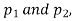 is the real one.
is the real one.
If z<2, the difference may be due to fluctuations of simple sampling.
But if z lies between 2 and 3, then the difference is significant at a 5% level of significance.
(b)If the proportions of A's are not the same in the two populations from which the samples are drawn but 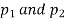 are the True values of proportions then S.E., e of the difference
are the True values of proportions then S.E., e of the difference 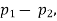 is given by
is given by
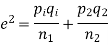
If 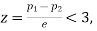 the difference could have risen due to fluctuations of simple sampling.
the difference could have risen due to fluctuations of simple sampling.
Example. In two large populations, there are 30% and 25% respectively of fair-haired people. Is this difference likely to be hidden in samples of 1200 and 900 respectively from the two populations?
Solution. Here 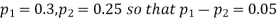
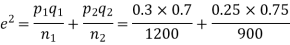
So that,.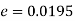
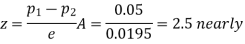
Hence it is unlikely that the real difference will be hidden.
Example. One type of aircraft is found to develop engine trouble in 5 flights out of a total of hundred and another type in 7 flights out of a total of 200 flights. is there a significant difference in the two types of aircraft so as far as engine defects are concerned.
Solution. 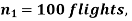 number of troubled flights =5
number of troubled flights =5
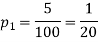
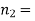 200 flights, number of troubled flights
200 flights, number of troubled flights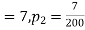
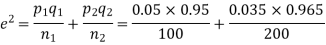
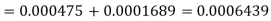
e=0.0254
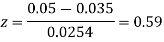
z<1, the difference is not significant.
Example. In a sample of 600 men from a certain City 450 are found, smokers. In another sample of 900 men from another City, 450 are smokers. do the data indicate that the cities are significantly different with respect to the habit of smoking among men.
Solution. 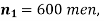 number of smokers = 450,
number of smokers = 450, 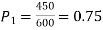
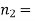 900 men, number of smokers = 450,
900 men, number of smokers = 450, 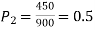
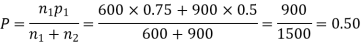
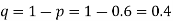
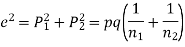
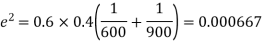
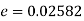
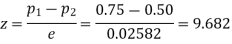
z>3 so that the difference is significant.
Significance test of the difference between the sample mean
Given two independent samples, 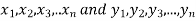 which means
which means 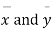 and standard deviations from a normal population with the same variance, we have to test the hypothesis that the population means
and standard deviations from a normal population with the same variance, we have to test the hypothesis that the population means 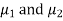 are the same
are the same
For this, we calculate,
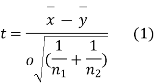
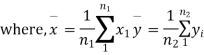
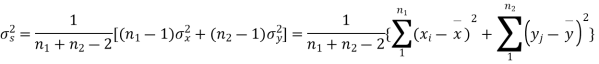
It can be shown that the variate t defined by (1) follows the t distribution with 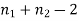 degree of freedom.
degree of freedom.
If the calculated value of 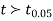 the difference between the sample means is said to be significant at a 5% level of significance.
the difference between the sample means is said to be significant at a 5% level of significance.
If 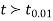 , the difference is said to be significant at a 1% level of significance.
, the difference is said to be significant at a 1% level of significance.
If 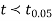 , the data is said to be consistent with the hypothesis, that
, the data is said to be consistent with the hypothesis, that 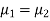
Cor. If the two samples are of the same size and the data are paired, then t is defined by
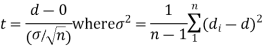
Example. From a random sample of 10 pigs fed on diet A. The increase in weight in a certain period were 10, 6, 16, 17, 13, 12, 8, 14, 15, 9 lbs. For another random sample of 12 pig’s fat on diet B, the increases in the same period were 7, 13, 22, 15, 12, 14, 18, 8, 21, 23, 10, 17 lbs. Test whether diets A and B differ significantly as regards their effects on weight increases?
Solution. We calculate the means and standard deviation of the samples as follows
| Diet A |
|
| Diet B |
|
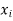 | 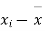 | 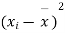 | 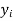 | 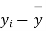 | 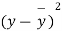 |
10 | -2 | 4 | 7 | -8 | 64 |
6 | -6 | 36 | 18 | -2 | 4 |
16 | 4 | 16 | 22 | 7 | 49 |
17 | 5 | 25 | 15 | 0 | 0 |
13 | 1 | 1 | 12 | -3 | 9 |
12 | 0 | 0 | 14 | -1 | 1 |
8 | -4 | 16 | 18 | 3 | 9 |
14 | 2 | 4 | 8 | -7 | 49 |
15 | 3 | 9 | 21 | 6 | 36 |
9 | -3 | 9 | 23 | 8 | 64 |
|
|
| 10 | -5 | 25 |
|
|
| 23 | 2 | 4 |
120 | 0 | 120 | 10 | 0 | 314 |
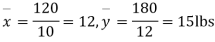
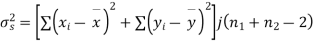
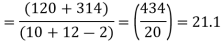
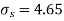
Assuming that the samples do not differ in weight so far as two diets are concerned i.e. 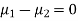
Hence, 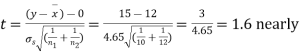
Here, 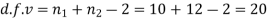
For 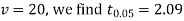
The calculated value of 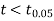
Hence the difference between the sample means is not significant that is the two diets do not differ significantly as regards their effects on the increase in weight.
Key takeaways-
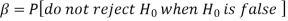
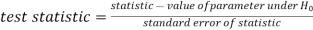
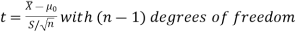
References
1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.
2. N.P. Bali and Manish Goyal, A textbook of Engineering Mathematics, Laxmi Publications.
3. Higher engineering mathematic, Dr. B.S. Grewal, Khanna publishers