Unit-5
Numerical Methods
This method is consists of finding the root of the equation 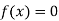 which lie between a and b (say).
which lie between a and b (say).
The function 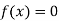 is a continuous function between a and b and f (a) and f (b) are of opposite signs then there is a least one root between a and b.
is a continuous function between a and b and f (a) and f (b) are of opposite signs then there is a least one root between a and b.
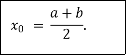 Suppose f (a) is negative and f (b) is positive, then the first approximate value of the root is
Suppose f (a) is negative and f (b) is positive, then the first approximate value of the root is
If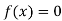 , then the correct root is
, then the correct root is 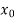 .But if
.But if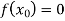 , then the root either lie between a and
, then the root either lie between a and 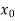 or
or 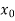 and b according to
and b according to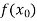 is positive or negative, we again bisect the interval as above and the process is repeated the root is found to the desired accuracy.
is positive or negative, we again bisect the interval as above and the process is repeated the root is found to the desired accuracy.
Note: Remember that root of an equation lie between its positive and negative values and we take an average of them to come closer to its accurate root.
Example1 Find a real root of 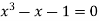 using bisection method correct to five decimal places.
using bisection method correct to five decimal places.
Let 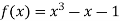 then by hit and trial we have
then by hit and trial we have
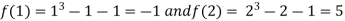
Thus 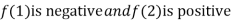 .So the root of the given equation should lie between 1 and 2.
.So the root of the given equation should lie between 1 and 2.

Now, 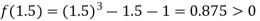
I.e. positive so the root of the given equation must lie between 

Now, 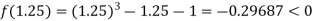
I.e. negative so the root of the given equation lie between 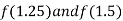
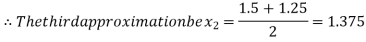
Now, 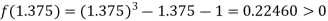
i.e. positive so the root of the given equation lie between 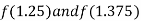
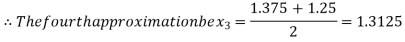
Now, 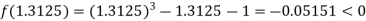
i.e. negative so that the root of the given equation lie between 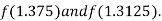
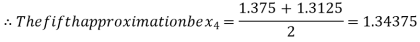
Now, 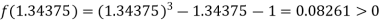
i.e. positive so that the root of the given equation lie between 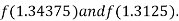
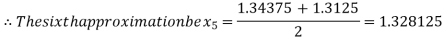
Now, 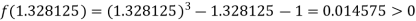
i.e. positive so that the root of the given equation lie between 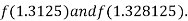
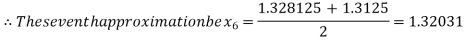
Now, 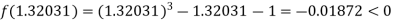
I.e. negative so that the root of the given equation lie between 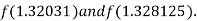
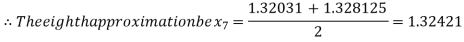
Now, 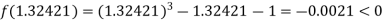
i.e. negative so that the root of the given equation lie between 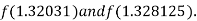
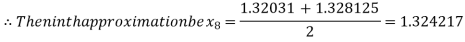
Hence the approximate root of the given equation is 1.32421
Example2 Find the root of the equation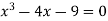 , using the bisection method.
, using the bisection method.
Let 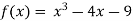 then by hit and trial we have
then by hit and trial we have
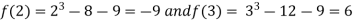
Thus 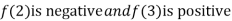 .So the root of the given equation should lie between 2 and 3.
.So the root of the given equation should lie between 2 and 3.

Now, 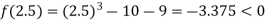
i.e. negative so the root of the given equation must lie between 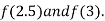

Now, 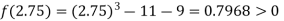
i.e. positive so the root of the given equation must lie between 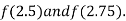
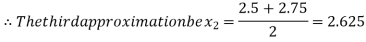
Now, 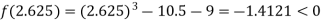
i.e. negative so the root of the given equation must lie between 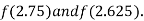
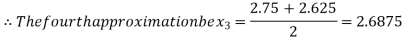
Now, 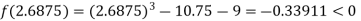
i.e. negative so the root of the given equation must lie between 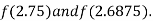
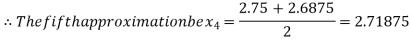
Now, 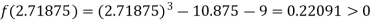
i.e. positive so the root of the given equation must lie between 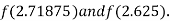
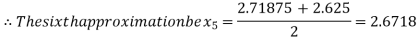
Now, 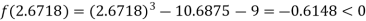
i.e. negative so the root of the given equation must lie between 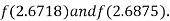
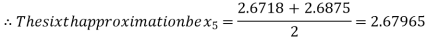
Hence the root of the given equation correct to two decimal places is 2.67965.
Example3 Find the root of the equation 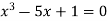 between 2 and 3, using bisection method correct to two decimal places.
between 2 and 3, using bisection method correct to two decimal places.
Let 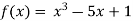
Where 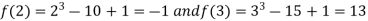
Thus 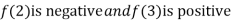 .So the root of the given equation should lie between 2 and 3.
.So the root of the given equation should lie between 2 and 3.

Now, 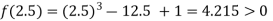
i.e. positive so the root of the given equation must lie between 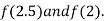

Now, 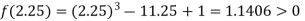
i.e. positive so the root of the given equation must lie between 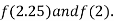
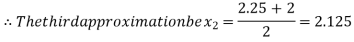
Now, 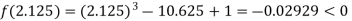
i.e. negative so the root of the given equation must lie between 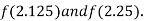
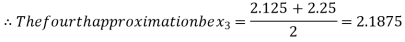
Now, 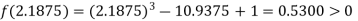
i.e. positive so the root of the given equation must lie between 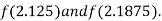
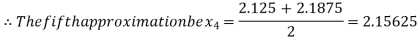
Now, 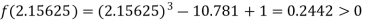
i.e. positive so the root of the given equation must lie between 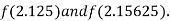
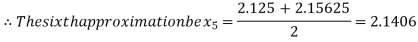
Now, 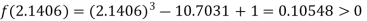
i.e. positive so the root of the given equation must lie between 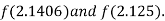
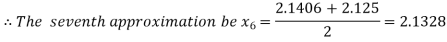
Now, 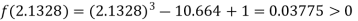
i.e. positive so the root of the given equation must lie between 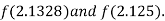
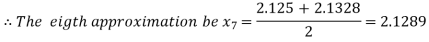
Now, 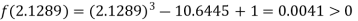
i.e. positive so the root of the given equation must lie between 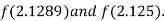
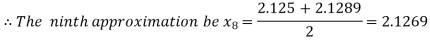
Hence the root of the given equation correct to two decimal places is 2.1269
This method is an improvement over the Regula Falsi Method as it does not require the condition 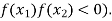
The general formula for successive approximation is,
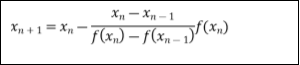
Where 
We keep on calculating until we get the desired root to the correct decimal places.
Example1 Using the Secant Method find the root of the equation correct to three decimal places
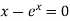
Let 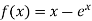
By Secant Method
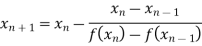
Let the initial approximation be 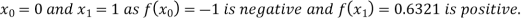
For n=1, the first approximation 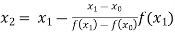
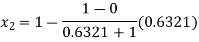
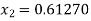
Now, 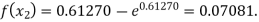
For n=2, the second approximation 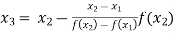
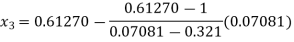
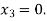 563839
563839
Now, 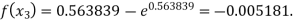
For n=3, the third approximation 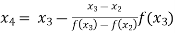
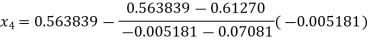
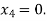 56717
56717
Now, 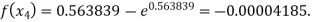
For n=4, the fourth approximation 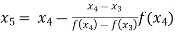
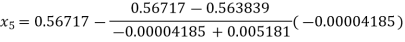
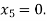 567143
567143
Hence the root of the given equation correct to four decimal places is 0.5671.
Example2 Using the Secant Method to find the root of the equation correct to four decimal places 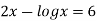
Let 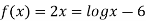
By Secant Method
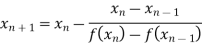
Let the initial approximation be 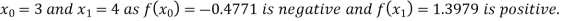
For n=1, the first approximation 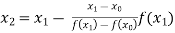
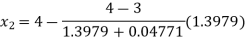
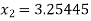
Now, 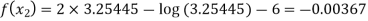
For n=2, the second approximation 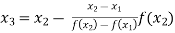
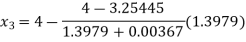
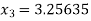
Now, 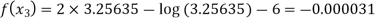
For n=3, the third approximation 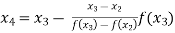
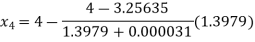
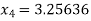
Hence the root of the given equation correct to four decimal places is 3.25636
Example3 Using the Secant Method find the root of the equation correct to four decimal place
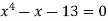
Let 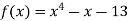
By Secant Method
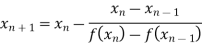
Let the initial approximation be 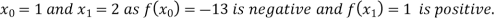
For n=1, the first approximation 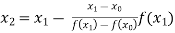
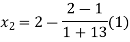
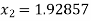
Now, 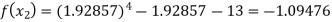
So the root of the equation lies between 2 and 1.92857
For n=2, the second approximation,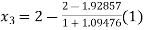
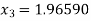
Now, 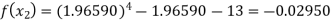
So the root of the equation lie between 2 and 1.96590
For n=3, the third approximation
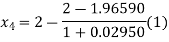
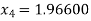
Now, 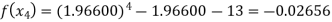
So the root of the equation lie between 2 and 1.96600
For n=4, the fourth approximation
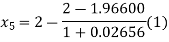
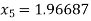
Now, 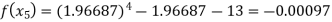
So the root of the equation lie between 2 and 1.96687
For n=5, the fifth approximation
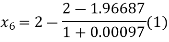
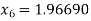
Now, 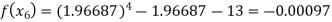
So the root of the equation lie between 2 and 1.96690
For n=6, the sixth approximation
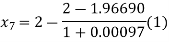
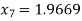
Now, 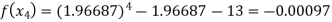
Hence the root of the given equation correct to four decimal places is 1.9669.
Key takeaways-
The general formula for successive approximation is,
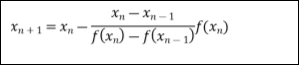
Where 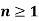
This is the oldest method of finding the approximate numerical value of a real root of an equation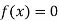 .
.
In this method, we suppose that 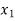 and
and 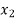 are two points where
are two points where 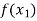 and
and 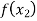 are of opposite sign.Let
are of opposite sign.Let 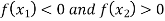
 Hence the root of the equation
Hence the root of the equation 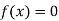 lie between
lie between 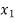 and
and 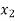 and so,
and so, 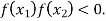
The Regula Falsi formula
Find 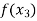 is positive or negative. If
is positive or negative. If 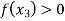 then root lie between
then root lie between 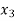 and
and 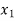 or if
or if 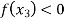 then root lies between
then root lies between 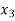 and
and 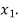 similarly, we calculate
similarly, we calculate 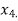
Proceed in this manner until the desired accurate root is found.
Example1Find a real root of the equation 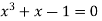 near
near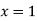 , correct to three decimal places by the Regula Falsi method.
, correct to three decimal places by the Regula Falsi method.
Let 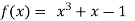
Now, 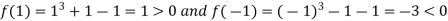
And also 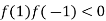
Hence the root of the equation 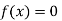 lie between
lie between 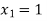 and
and 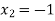 and so,
and so, 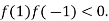
By Regula Falsi Method
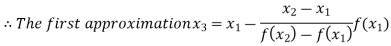
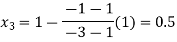
Now, 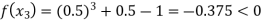
So the root of the equation 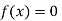 lie between 1 and 0.5 and so
lie between 1 and 0.5 and so 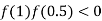
By Regula Falsi Method
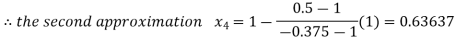
Now, 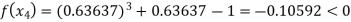
So the root of the equation 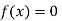 lie between 1 and 0.63637 and so
lie between 1 and 0.63637 and so 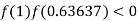
By Regula Falsi Method
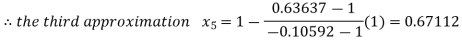
Now, 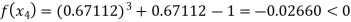
So the root of the equation 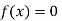 lie between 1 and 0.67112 and so
lie between 1 and 0.67112 and so 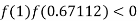
By Regula Falsi Method
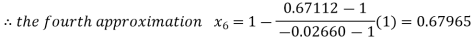
Now, 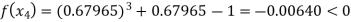
So the root of the equation 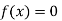 lie between 1 and 0.63636 and so
lie between 1 and 0.63636 and so 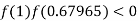
By Regula Falsi Method
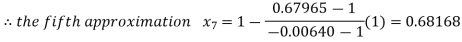
Now, 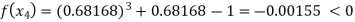
So the root of the equation 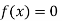 lie between 1 and 0.68168 and so
lie between 1 and 0.68168 and so 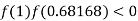
By Regula Falsi Method
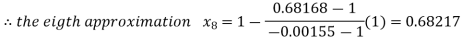
Now, 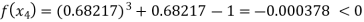
Hence the approximate root of the given equation near 1 is 0.68217
Example2 Find the real root of the equation
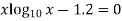
By the method of false position correct to four decimal places
Let 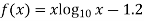
By hit and trail method
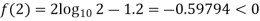
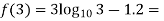 0.23136 > 0
0.23136 > 0
So, the root of the equation 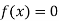 lie between
lie between 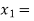 2 and
2 and 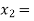 3 and also
3 and also 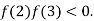
By Regula Falsi Method
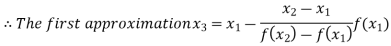
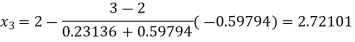
Now, 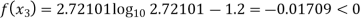
So, the root of the equation 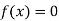 lies between 2.72101 and 3 and also
lies between 2.72101 and 3 and also 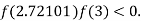
By Regula Falsi Method
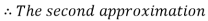
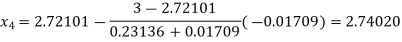
Now, 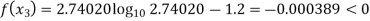
So, the root of the equation 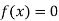 lies between 2.74020 and 3 and also
lies between 2.74020 and 3 and also 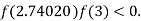
By Regula Falsi Method
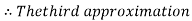
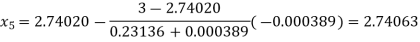
Now, 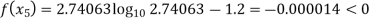
So, the root of the equation 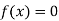 lies between 2.74063 and 3 and also
lies between 2.74063 and 3 and also 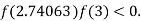
By Regula Falsi Method
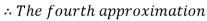

Hence the root of the given equation correct to four decimal places is 2.7406
Example3 Apply Regula Falsi Method to solve the equation
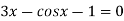
Let 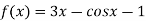
By hit and trail
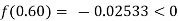
And 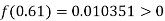
So the root of the equation lie between 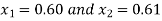 and also
and also 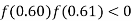
By Regula Falsi Method
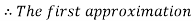
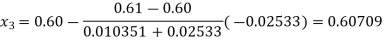
Now, 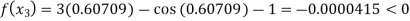
So, the root of the equation 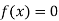 lies between 0.60709 and 0.61 and also
lies between 0.60709 and 0.61 and also 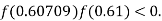
By Regula Falsi Method
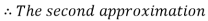

Now, 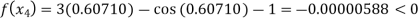
So, the root of the equation 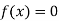 lies between 0.60710 and 0.61 and also
lies between 0.60710 and 0.61 and also 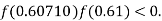
By Regula Falsi Method
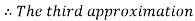
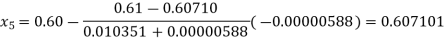
Hence the root of the given equation correct to five decimal places is 0.60710.
Key takeaways-
The Regula Falsi formula
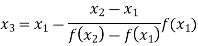
Let 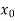 be the approximate root of the equation
be the approximate root of the equation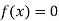 .
.
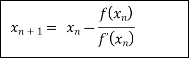 By Newton Raphson formula
By Newton Raphson formula 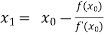
In general,
Where n=1, 2, 3…… we keep on calculating until we get the desired root to the correct decimal places.
Example1 Using the Newton-Raphson method, find a root of the following equation correct to 3 decimal places: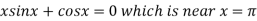 .
.
Given 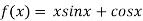
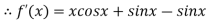
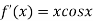
By Newton- Raphson Method
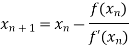
= 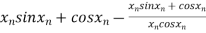
=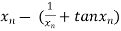
The initial approximation is 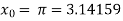 in radian.
in radian.
For n =0, the first approximation 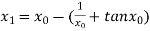
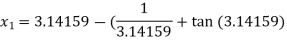
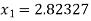
For n =1, the second approximation 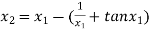
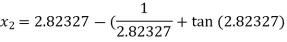
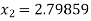
For n =2, the third approximation 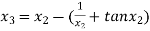
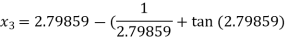
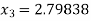
For n =3, the fourth approximation 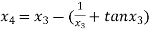
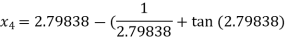
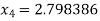
Hence the root of the given equation correct to five decimal places 2.79838.
Example2 Using the Newton-Raphson method, find a root of the following equation correct to 3 decimal places: 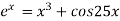 near to 4.5
near to 4.5
Let 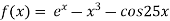
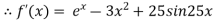
The initial approximation 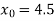
By Newton Raphson Method
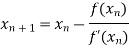
For n =0, the first approximation 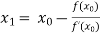
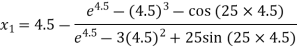
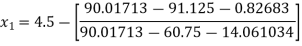
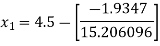
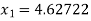
For n =1, the second approximation 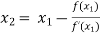
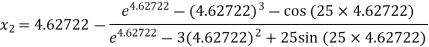
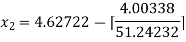
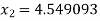
For n =2, the third approximation 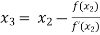
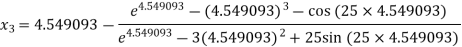
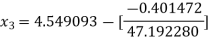
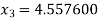
For n =3, the fourth approximation 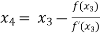
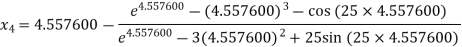
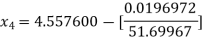
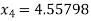
Hence the root of the equation correct to three decimal places is 4.5579
Example3 Using the Newton-Raphson method, find a root of the following equation correct to 4 decimal places: 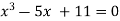
Let 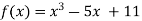
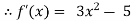
By Newton Raphson Method
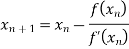
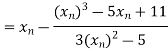
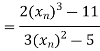
Let the initial approximation be 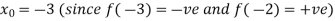
For n=0, the first approximation 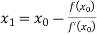
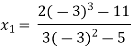
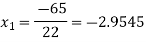
For n=1, the second approximation 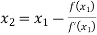
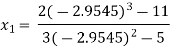
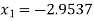
For n=2, the third approximation 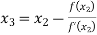
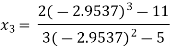
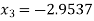
Since 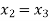 therefore the root of the given equation correct to four decimal places is -2.9537
therefore the root of the given equation correct to four decimal places is -2.9537
Successive Approximation Method:
The successive approximation is also known as the iteration method. To start the solution using this method we need one or more approximate values which is not necessarily the root of the given equation.
We are finding the root of the given equation
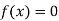 ..(1)
..(1)
We rewrite the given equation in the form
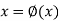 ..(2)
..(2)
We know that the root of the equation lie between its positive and the negative values
Let 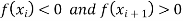
So, the interval of the root of the equation be 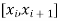 .
.
Now, let 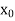 be an approximate root of the given equation (1).
be an approximate root of the given equation (1).
Putting it in equation (2) we get 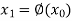
Successive substitution give the approximations
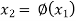
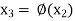
…………..
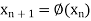
If the above values converge to a definite number then that number will be the root of the given equation.
Example1: Find the real root of the equation
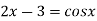
Correct to three decimal places in the interval 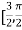 ]
]
The given equation is 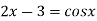 ..(1)
..(1)
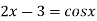
Or 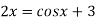
Or 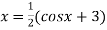 =
= 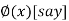 ..(2)
..(2)
Or 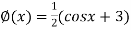
Let 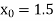 , in the interval
, in the interval 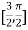 .
.
The successive approximation we have
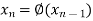
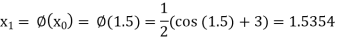
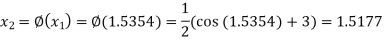
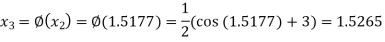
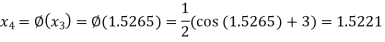
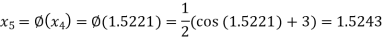
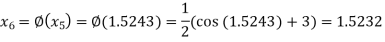
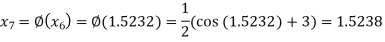
Hence the root of the equation correct to three decimal places is 1.524.
Example2: Find the real root of the polynomial 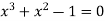 correct to three decimal places?
correct to three decimal places?
Given equation 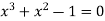 ….(1)
….(1)
Here 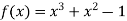
Also 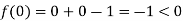
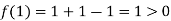
Therefore the root of the equation lies between 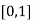 .
.
Again 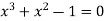
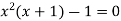
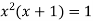
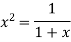
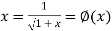 ….(2)
….(2)
Let 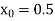 , in the interval
, in the interval 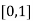 .
.
The successive approximation we have
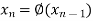
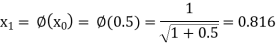
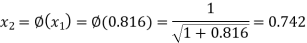
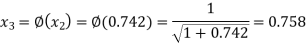
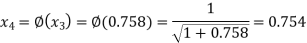
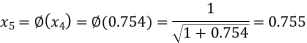
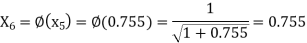
Hence the root of the equation correct to three decimal places is 0.755.
Example3: By iteration method, find the value of 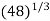 , correct to three decimal places.
, correct to three decimal places.
Let 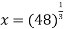
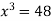
Let 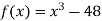 .
.
Also 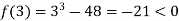
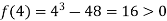
Therefore the root of the equation lie between 3 and 4.
Given equation can rewrite 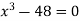 .
.
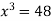
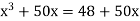
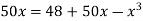
Or 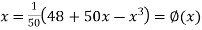 …(2)
…(2)
Let 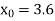 , in the interval
, in the interval 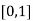 .
.
The successive approximation we have
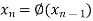
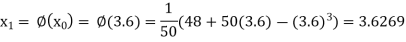
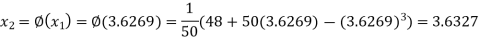
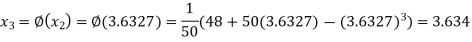
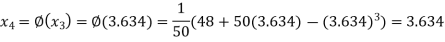
Hence the root of the equation correct to three decimal places is 3.634.
Convergence and stability-
Convergence-
A sequence of iterates 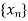 is said to converge with order
is said to converge with order 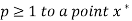 if
if
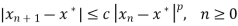
For some constant c > 0.
Note-
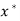
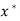
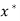
Stability-
Let there are n steps to evaluate a function. Then the total process of evaluating this function is said to have instability if at least one step is ill-conditioned. If all the steps are well-conditioned, then the process is said to be stable.
In this method, we eliminate successively the unknown 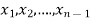 so that the equation (1) remain with the single unknown
so that the equation (1) remain with the single unknown 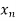 and reduce to the upper triangular system. At last with help of back substitution, we calculate the values of the remaining unknowns.
and reduce to the upper triangular system. At last with help of back substitution, we calculate the values of the remaining unknowns.
Consider a system of n linear equation in n unknown 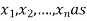
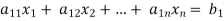
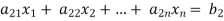
… …… ….. … (1)
… …… …. …
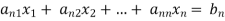
To convert the above system into an upper triangular matrix we eliminate 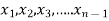 from the second, third, fourth …., n equations above by multiplying the first equation by
from the second, third, fourth …., n equations above by multiplying the first equation by 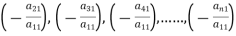 added them to the corresponding equations second, third, fourth,…., n equation. We get
added them to the corresponding equations second, third, fourth,…., n equation. We get
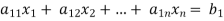
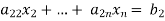
… …… ….. …
… …… …. …
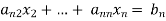
Repeating the above method for 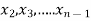 we get finally the upper triangular form.
we get finally the upper triangular form.
Upper Triangular form of above
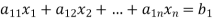
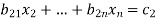
……………………….. (i)
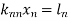
Thus 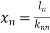 .
.
Then we calculate the values of 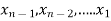 .
.
Example1 Apply Gauss Elimination method to solve the equations:
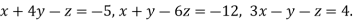
Given Check Sum (sum of coefficient and constant)
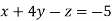 -1 …. (I)
-1 …. (I)
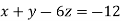 -16 …. (ii)
-16 …. (ii)
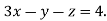 5 …. (iii)
5 …. (iii)
(I)We eliminate x from (ii) and (iii)
Apply eq(ii)-eq(i) and eq(iii)-3eq(i) we get
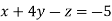 -1 ….(i)
-1 ….(i)
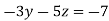 -15 ….(iv)
-15 ….(iv)
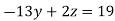 8 ….(v)
8 ….(v)
(II) We eliminate y from eq(v)
Apply 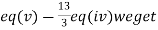
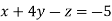 -1 ….(i)
-1 ….(i)
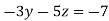 -15 ….(iv)
-15 ….(iv)
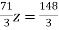 73 ….(vi)
73 ….(vi)
(III) Back Substitution we get
From (vi) we get 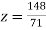
From (iv) we get 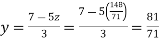
From (i) we get 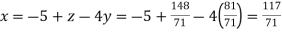
Hence the solution of the given equation is 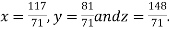
Example2 Solve the equation by Gauss Elimination Method:
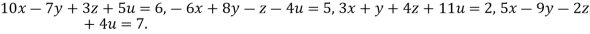
Given 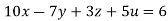
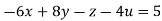
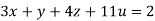
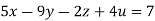
Rewrite the given equation as
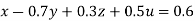 … (i)
… (i)
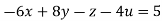 ….(ii)
….(ii)
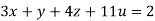 ….(iii)
….(iii)
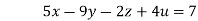 …(iv)
…(iv)
(I) We eliminate x from (ii),(iii) and (iv) we get
Apply eq(ii) + 6eq(i), eq(iii) -3eq(i), eq(iv)-5eq(i) we get
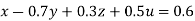 …(i)
…(i)
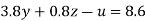 ….(v)
….(v)
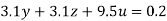 ….(vi)
….(vi)
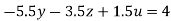 …(vii)
…(vii)
(II) We eliminate y from (vi) and (vii) we get
Apply 3.8 eq(vi)-3.1eq(v) and 3.8eq(vii)+5.5eq(v) we get
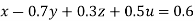 …(i)
…(i)
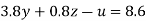 ….(v)
….(v)
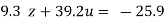 …(viii)
…(viii)
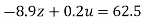 …(ix)
…(ix)
(III) We eliminate z from eq (ix) we get
Apply 9.3eq (ix) + 8.3eq (viii), we get
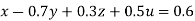 … (i)
… (i)
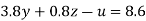 ….(v)
….(v)
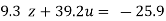 …(viii)
…(viii)
350.74u=350.74
Or u = 1
(IV) Back Substitution
From eq(viii) 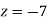
Form eq(v), we get 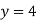
From eq(i) , 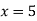
Hence the solution of the given equation is x=5, y=4, z=-7 and u=1.
Example3
Apply Gauss Elimination Method to solve the following system of the equation: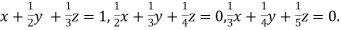
Given 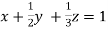 … (i)
… (i)
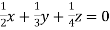 … (ii)
… (ii)
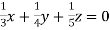 … (iii)
… (iii)
(I) We eliminate x from (ii) and (iii)
Apply 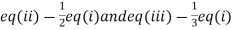 we get
we get
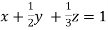 … (i)
… (i)
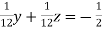 … (iv)
… (iv)
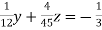 … (v)
… (v)
(II) We eliminate y from (v)
Apply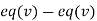 we get
we get
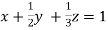 … (i)
… (i)
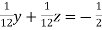 … (vi)
… (vi)
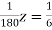 … (vii)
… (vii)
(III) Back substitution
From (vii) 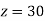
From (vi) 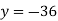
From (i) 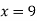
Hence the solution of the equation is 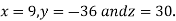
The method is based on the fact that every matrix A can be expressed as the product of a lower triangular matrix and an upper triangular matrix, provided all the principal minors of A are non-singular.
Which means-
If 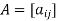 , then-
, then-
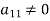

Now consider the equations-
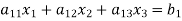
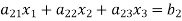
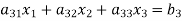
We can write it as-
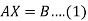
Where-
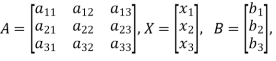
Let
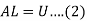
Where-
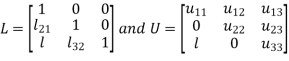
Equation (1) becomes-
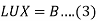
Writing-
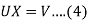
Equation (3) becomes-
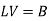 which is equivalent to the equations-
which is equivalent to the equations-
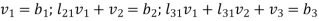
Solving these for 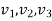 we know V. Then equation (4) becomes-
we know V. Then equation (4) becomes-
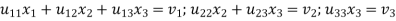
From which 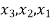 can be found by back substitution.
can be found by back substitution.
We write (2) as to find the matrix L and U-
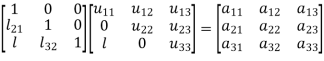
Multiplying the matrix on the left and equating corresponding elements from both sides, we get-
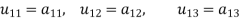
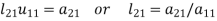
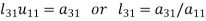
3. 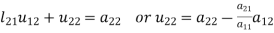
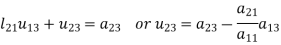
4. 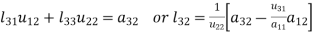
5. 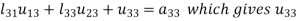
We compute the elements of L and U in the following manner-
Example: Solve the equations-
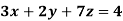
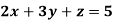
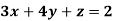
Sol.
Let

So that-
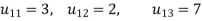
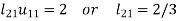
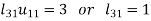
3. 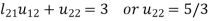
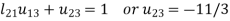
4. 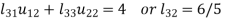
5. 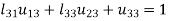
So
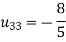
Thus-
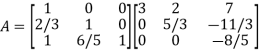
Writing UX = V,
The system of given equations become-
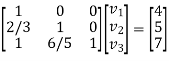
By solving this-
We get-
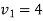
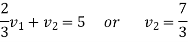
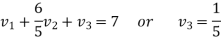
Therefore the given system becomes-
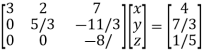
Which means-
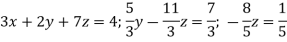
By back substitution, we have-
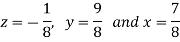
Jacobi’s Iteration method:
Let us consider the system of simultaneous linear equation
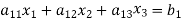
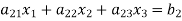 (1)
(1)
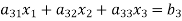
The coefficients of the diagonal elements are larger than all other coefficients and are non-zero. Rewrite the above equation we get
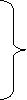
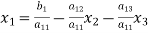
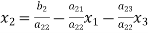 (2)
(2)
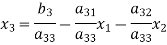
Take the initial approximation 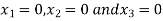 we get the values of the first approximation of
we get the values of the first approximation of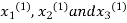 .
.
By the successive iteration, we will get the desired result.
Example1Use Jacobi’s method to solve the system of equations:
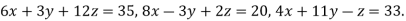
Since 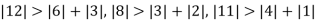
So, we express the unknown with a large coefficient in terms of other coefficients.
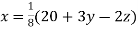
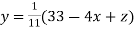 (1)
(1)
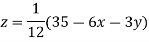
Let the initial approximation be 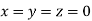
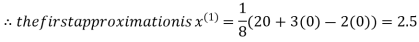
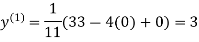
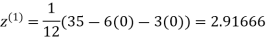
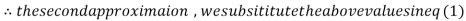
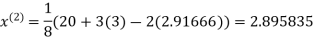
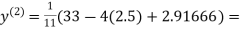 2.35606
2.35606
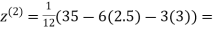 0.91666
0.91666
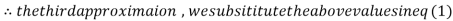
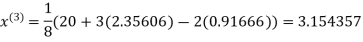
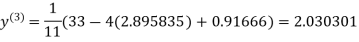
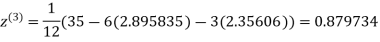
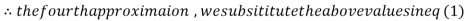
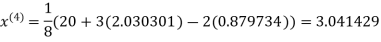
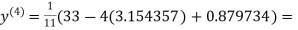 1.932936
1.932936
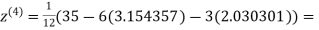 0.831912
0.831912
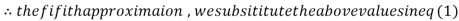
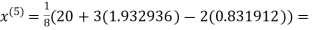 3.016873
3.016873
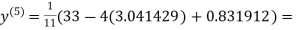 1.969654
1.969654
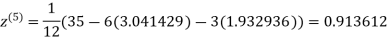
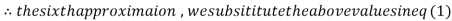
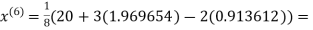 3.010217
3.010217
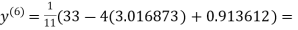 1.986010
1.986010
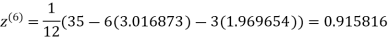
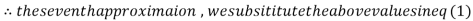
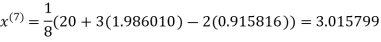
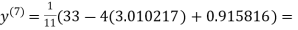 1.988631
1.988631
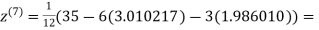 0.915055
0.915055
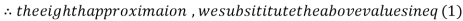
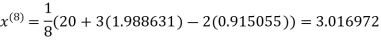
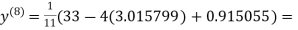 1.986532
1.986532
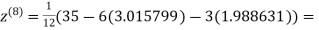 0.911609
0.911609
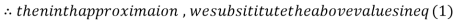
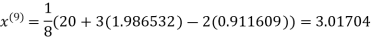
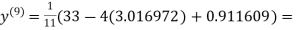 1.985792
1.985792
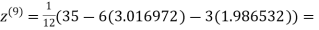 0.911547
0.911547
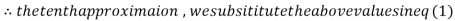
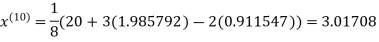
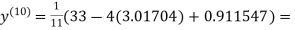 1.98576
1.98576
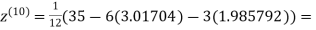 0.911698
0.911698
Since the approximation in the ninth and tenth iteration is the same up to three decimal places, hence the solution of the given equations is 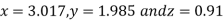
Example2 Solve by Jacobi’s Method, the equations
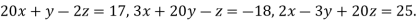
Given equation can be rewritten in the form
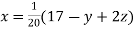 … (i)
… (i)
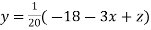 ..(ii)
..(ii)
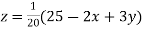 ..(iii)
..(iii)
Let the initial approximation be 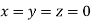
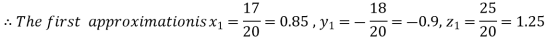
Putting these values on the right of the equation (i), (ii), and (iii) and so we get
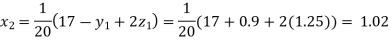
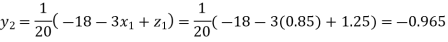
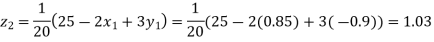
Putting these values on the right of the equation (i), (ii), and (iii) and so we get
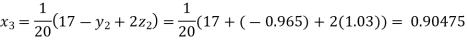
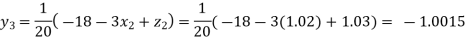
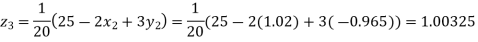
Putting these values on the right of the equation (i), (ii), and (iii) and so we get
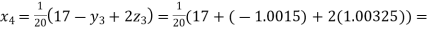 0.90025
0.90025
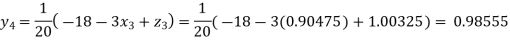
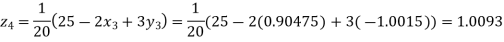
Putting these values on the right of the equation (i), (ii), and (iii) and so we get
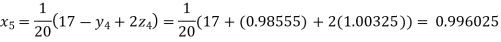
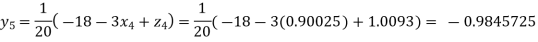
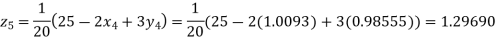
Putting these values on the right of the equation (i), (ii), and (iii) and so we get
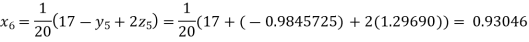
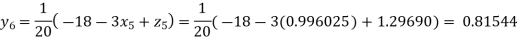
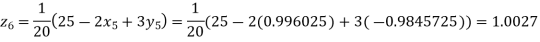
Hence solution approximately is 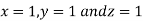
Example3Use Jacobi’s method to solve the system of the equations
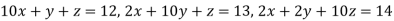
Rewrite the given equations
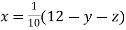
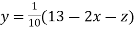 (1)
(1)
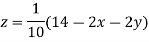
Let the initial approximation be 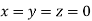
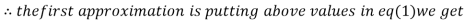
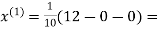 1.2
1.2
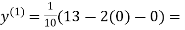 1.3
1.3
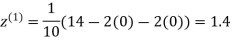
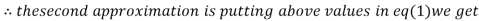
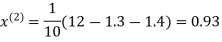
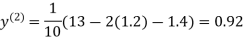
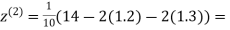 0.9
0.9

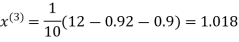
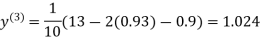
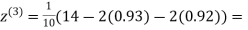 1.03
1.03
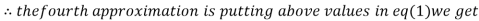
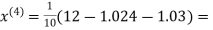 0.9946
0.9946
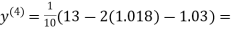 0.9934
0.9934
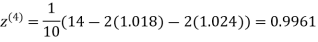

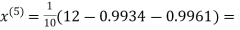 1.0015
1.0015
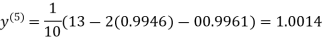
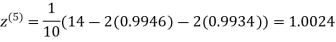
Hence the solution of the above equation correct to two decimal places is
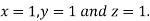
Gauss-Seidel method:
This is the modification of Jacobi’s Iteration. As above in Jacobi’s Iteration, we take first approximation as 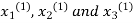 and put in the right-hand side of the first equation of (2) and let the result be
and put in the right-hand side of the first equation of (2) and let the result be 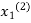 . Now we put
. Now we put 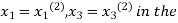 right-hand side of the second equation of (2) and suppose the result is
right-hand side of the second equation of (2) and suppose the result is 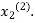 now put
now put 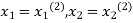 in the RHS of the third equation of (2) and suppose the result be
in the RHS of the third equation of (2) and suppose the result be 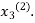 the above method is repeated till the values of all the unknown are found up to the desired accuracy.
the above method is repeated till the values of all the unknown are found up to the desired accuracy.
Example1 Use the Gauss-Seidel Iteration method to solve the system of equations
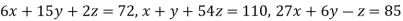
Since 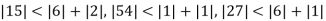
So, we express the unknown of larger coefficients in terms of the unknowns with smaller coefficients.
Rewrite the above system of equations
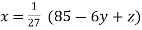
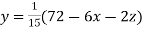 (1)
(1)
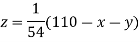
Let the initial approximation be 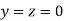
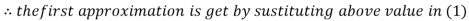
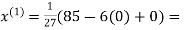 3.14814
3.14814
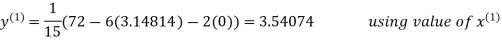
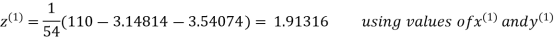
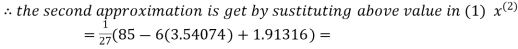 2.43217
2.43217
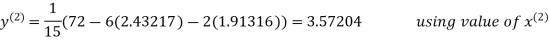
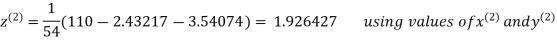
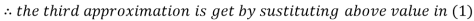
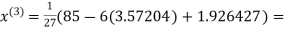 2.42571
2.42571
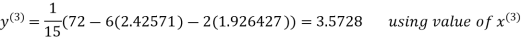
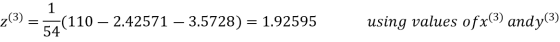
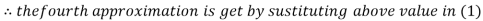
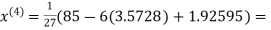 2.4260
2.4260
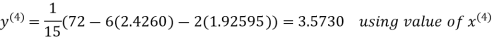
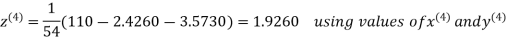
Hence the solution correct to three decimal places is
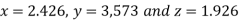
Example2 Solve the following system of equations
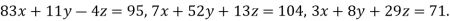 By Gauss-Seidel method.
By Gauss-Seidel method.
Rewrite the given system of equations as
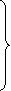
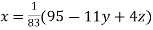
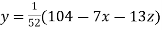 (1)
(1)
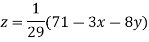
Let the initial approximation be 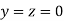
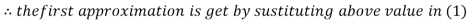
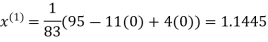
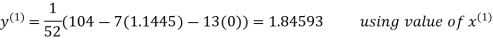
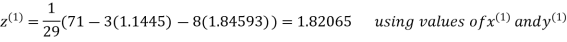
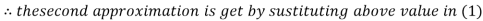
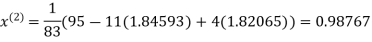
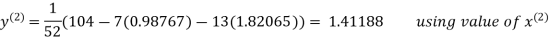
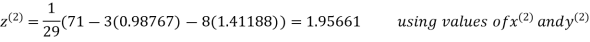
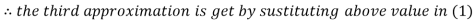
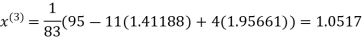
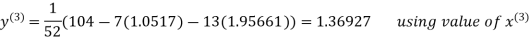
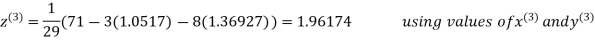
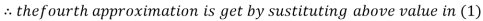
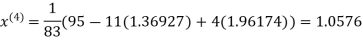
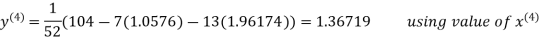
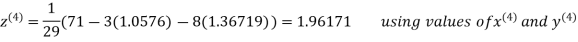
Thus the required solution is 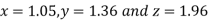
Example3 Solve the following equations by Gauss-Seidel Method
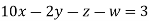
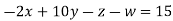
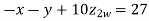
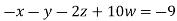
Rewrite the above system of equations
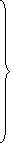
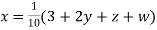
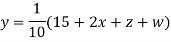
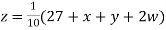 (1)
(1)
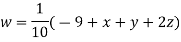
Let the initial approximation be 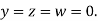

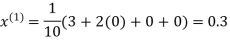
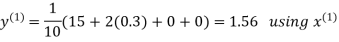
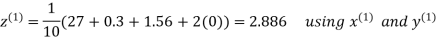
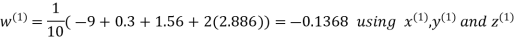

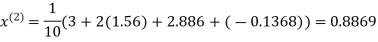
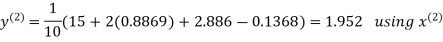
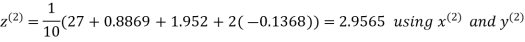
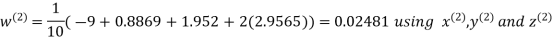

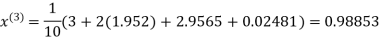
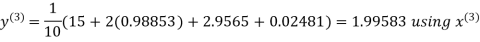
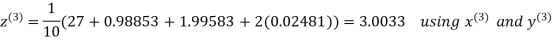
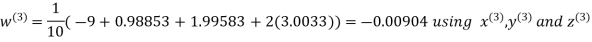

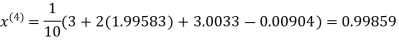
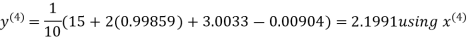
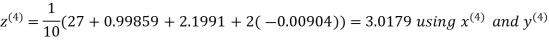
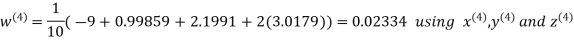

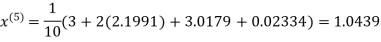
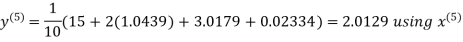
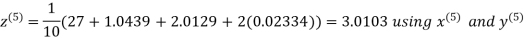
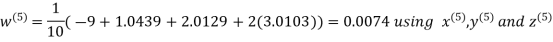
Hence the required solution is 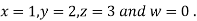
References
1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.
2. N.P. Bali and Manish Goyal, A textbook of Engineering Mathematics, Laxmi Publications.
3. Higher engineering mathematic, Dr. B.S. Grewal, Khanna publishers