Unit 1
Analysis of Algorithm
Basically algorithm is the finite steps to solve problem in computer.
It can be the set of instruction than performs certain task.
The collection of unambiguous instruction occurring in some specific sequence and such a procedure should produce output for a given set of input in finite amount of time is known as Algorithm.
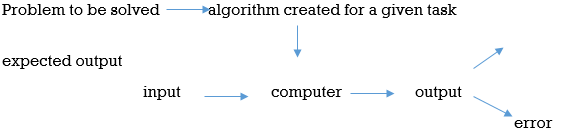
- Input : can be zero or more input
- Output : must produce output
- Finiteness : must have ending
- Definiteness : unambiguous and clear
- Effectiveness : should not be complex
It is formal way to speak about functions and classify them.
It is used to specify the running time and space complexity of algorithm and to frame the run time performance in mathematical computation.
It refers as boundation or framing into the mathematical terms.
As the algorithm having three cases according to time taken by program to perform a certain task.
- Worst case
- Best case
- Average case
Following are the asymptotic notations which are used to calculate the running time complexity of algorithm:
- Big Oh (O) notation
- Big Omega (ῼ) notation
- Theta (Ꙫ) notation
1.4.1 Big Oh Notation (O)
- It is the formal way to express the time complexity.
- It is used to define the upper bound of an algorithm’s running time.
- It shows the worst case time complexity or largest amount of time taken by the algorithm to perform a certain task.
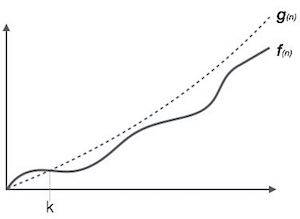
Here, f( n ) <= g( n ) ……………..(eq1)
Where n>= k , C>0 and k>=1
If any algorithm satisfies the eq1 condition then it becomes f ( n )= O ( g ( n ) )
1.4.2 Big Omega (ῼ) Notation
- It is the formal way to express the time complexity.
- It is used to define the lower bound of an algorithm’s running time.
- It shows the best case time complexity or best of time taken by the algorithm to perform a certain task.
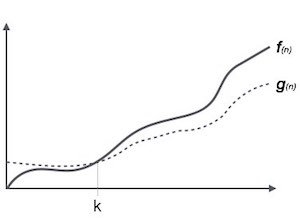
Here, f ( n ) >= g ( n )
Where n>=k and c>0, k>=1
If any algorithm satisfies the eq1 condition then it becomes f ( n )= ῼ ( g ( n ) )
1.4.3 Theta (Ꙫ) Notation
- It is the formal way to express the time complexity.
- It is used to define the lower as well as upper bound of an algorithm’s running time.
- It shows the average case time complexity or average of time taken by the algorithm to perform a certain task.
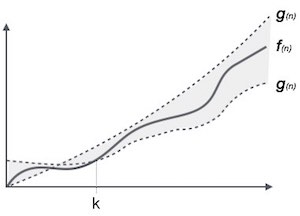
Let C1 g(n) be upper bound and C2 g(n) be lower bound.
C1 g(n)<= f( n )<=C2 g(n)
Where C1, C2>0 and n>=k
- Based on parameters n indicates the input size
- Identifies algorithm basic operation
- Determine worst, average, best case for input of size n
- Sum the number of basic operation executed
- Simplify the sum using standard formula and rules
Example:
Determine the value of the largest element in a given array.
Input: An array A [0, · · · , n − 1] of real numbers.
Output: The value of the largest element in A.
Algorithm:
MaxElement A[0, · · · n − 1])
Max = A[0]
For i = 1 to n – 1
Do
{
If A[i] > max then
Max = A[i]
}
Return (max)
- The algorithm that solves the problem by solving the one or more smaller instances of same problem.
- The problem can be solved by using the recursive and non-recursive functions.
- A recurrence is an equation or inequality that describes a function in terms of its vale over a small value.
Example:
Factorial function using recursive algorithm:
f(n) = n * f(n − 1)
Algorithm:
FindFact-β(n)
If n = 0
Then return (1)
Else
Return (n · FindFact − β(n − 1))
The analysis which used in occasional operation is very slow, but most of the operations which are executing very frequently are faster.
When first set if input does not affects the next set of input but when it affects to the running time of next set of input we go for amortized analysis.
For a dynamic array, items can be inserted at a given index in O (1) time.
But if that index is not present in the array, it fails to perform the task in constant time.
For that case, it initially doubles the size of the array then inserts the element if the index is present.