UNIT 3
DYNAMIC PROGRAMING
• Dynamic programing solves the solutions of sub-problems
• Dynamic programing applies when sub-problem overlaps
• It solves each sub-problem just ones and then saves answer in table.
• Dynamic programing follows the basic principle of optimality.
• The principle of optimality says that problem can solve by taking some decisions.
• In greedy method we take decisions at one time only but in dynamic we take decisions at every stage.
• Warshal’s algorithm constructs transitive closure of given directd graph.
• In directed graph there are n vertices.
• Warshal’s construct the transitive closure through series of matrices R0,R1,R2,….Rn and matrices order will be n*n.
• Rn become required transitive closure.
• Vertices are numbered from 1 to n.
• So the closure matrices series start from R0 then equation become
• R k[i,j]=R (k-1) [i,j]
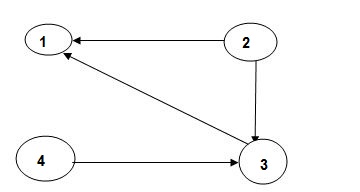

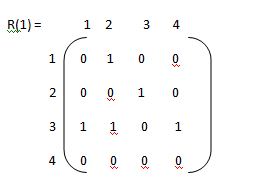
Now,
R(1) [i.j].R(0)[i,j] or (R(0)[i,1] & R(0) [1,j])
Step 1 :-
1st row --> 2 (element at place 2 )
1st col --> 3 (element at place 3 )
Now R = {3,2}


• Floyds algorithm is used to find shortest path from one node to all other nodes in the network.
• Hence it is also known as all pair shorteset path algorithm.
• Suppose there are four nodes such as A,B,C,D. If source node is A then it finds the shortest path from A to all other nodes in network as shown in figure given below.

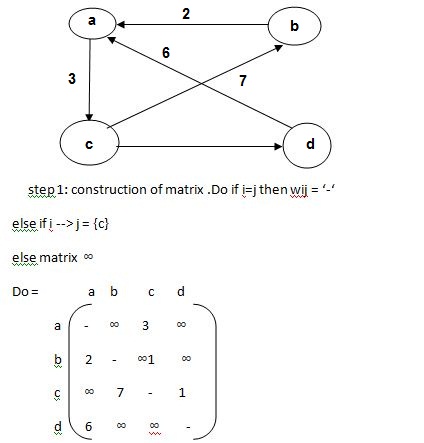
Step 2 :-
k-1 k-1 k-1
W ij k = min ( Wij . Wik + Wkj )
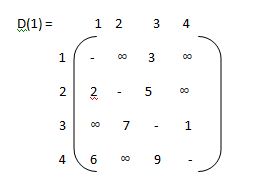
Step 3 :-
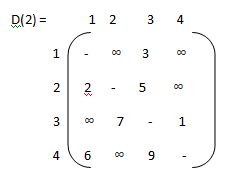
• Binary search tree is the rooted binary tree which is divided into sub-trees.
• Left node having lesser value than root and right node having the greater value than root.
• Optimal binary search tree is the tree with the minimum cost value.
Suppse we have inputs as keys and frequency.
Input [10,20,30]
Freq [3,2,5]
Following are the possibilities:
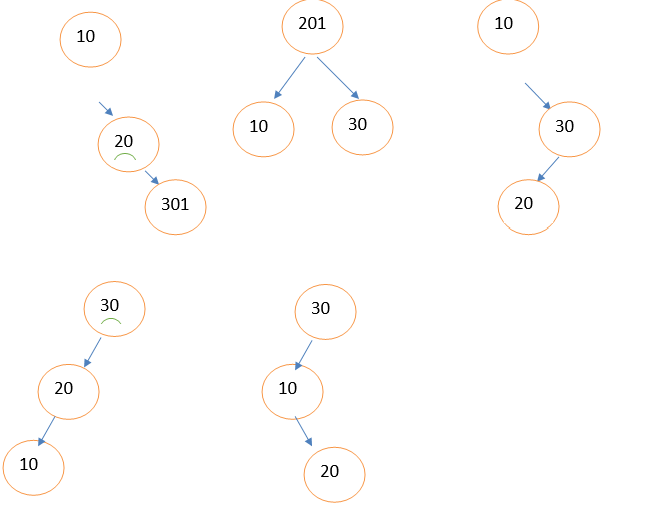
First BST having the value:
10----------------1*3=3
\ min value of BST is : 3+4+15=22
20------------2*2=4
\
30----------3*5=15
II= 20 III= 10 IV=30 V= 30
/ \ \ / /
10 30 30 20 10
/ / \
20 10 20
19 18 17 18
So among all BSTs, IV th BST has optimal solution as 17 is minimum cost value of binary tree.
• 0/1 knapsack problem is used to find the maximum profit from the items selected.
• 0/1 knapsack problem means we pick the item or not picking the item ie. We canot split the item.
• Item having the weight and the cost.
• Assume we are having many item then which item will give us profit more than we have ti check first.
• First sort the value to weight in non-increasing order and then pick the item.
Here I is row and j is column
If (j<wt[i])
T[i][j]=T[i-1][j]
Else
{
T[i][j]=max{val[i]+T[i-1][j-wt[i]]
Or
{T[i-1][j]
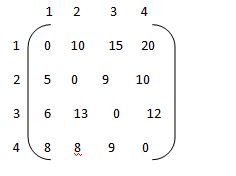
Here total weight =7
Value | Weight | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
4 | 3 | 0 | 1 | 1 | 4 | 5 | 5 | 5 | 5 |
5 | 4 | 0 | 1 | 1 | 4 | 5 | 6 | 6 | 9 |
7 | 5 | 0 | 1 | 1 | 4 | 5 | 7 | 8 | 9 |
• In travelling salesman problem start with source node travel all the nodes once and come back to the starting node and which path gives the minimum cost for travelling that becomes the optimal solution for travelling salesman problem.
• Formula:
• G(i,s)=min{Cik+ G( k, S- { k } )}
TSP Algorithm.
g (i,s) = min kϵs [Cik + g ( K , S – {K})]
Example :-
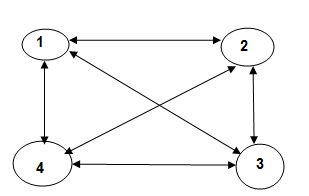
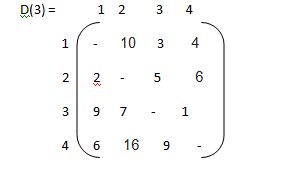

g ( 1, { 2,3,4})
= min kϵ{2,3,4} { C 1k , g (K,{2,3,4}-{k})}
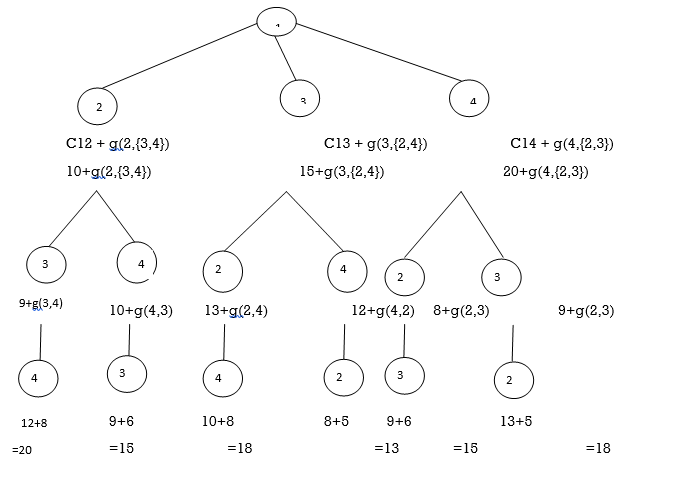
g(3,Φ)=6
g(4,Φ)=8
g(2,{3})=15
g(2,{4})=18
g(3,{2})=18
g(3,{4})=20
g(4,{2})=13
g(4,{3})=15
g(2,{3,4})=25
g(3,{2,4})=25
g(4,{3,2})=23
g(1,{2,3,4})=35
So the minimum optimal cost value from source node 1 to all other node is 35.