UNIT 4

BACKTRACKING

4.1 Backtracking

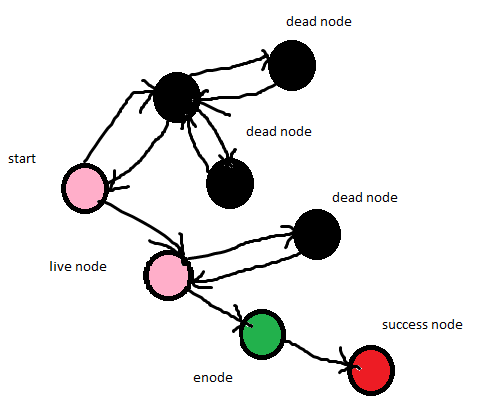
• It is a general algorithmic technique.
• Backtracking algorithm is used to solve a problem recursively to get a solution incrementally.
• It is used to solve problem in sequence of object is chosen from a specified set so that the sequence can satisfy some criteria.
• Backtracking is the systematic method which helps to trying out a sequence of decision until you find out that solution.
• It starts with one smaller piece at a time, if its solution get fail to satisfy the constraint then it can remove at any point of time.
• It searches for any possible combination in order to solve a computational problem.

• Two constraints :

1. Implicit constraint
2. Explicit constraint

• Application:

1. N-queen problem
2. Sum of subset
3. Graph coloring
4. Hamilton problems

4.2 Recursive Backtracking Algorithm

• When we are using the recursion we solve a problem by reducing it to a simpler problem of the same kind.
• The process continues until it reaches to the simple enough problems that can be solved directly.
• The simplest problem is known as base case that doesn’t make another call to method. Hence stops the recursion.

4.3 Non-Recursive Backtracking

• Iterative method is also known as non-recursive backtracking method.
• Recursive methods can often be easily converted to a non-recursive method that uses iteration.

Example:

Public static int sum(n)

{

// handle negative values of n here

Int sum = 0;

For (inti = 1; i <= n; i++) sum += i;

Return sum;

}

4.4 N-Queens Problem

• Let chess board having N*N cells.
• We need to place N queens in such a way that no queen is attacked by any other queen.
• The queen can attack horizontally, vertically and diagonally.So initially, we are having N*N unattacked cells where we can place the N queens.

Step 1: Place the first queen at a cell (i,j). Hence the unattacked cell is reduced and number of queens to be placed is N−1.

Step 2: Place the second queen on unattacked cell that will reduce the no. Of unattacked cells and no. Of queen to be placed become N-2.

The process continues until it satisfies the following condition.

1. The no. Of unattacked cell become 0
2. The no of queens to be placed is not 0.

Step 3: As it satisfies first condition given above then it’s over, we got a final solution.

But if the unattacked cells become 0, then we need to backtrack and remove last placed queen from its current place and place it at some another cell.

This process will be done recursively.

Example:

8-Queen problem

• The eight queens problem is the problem of placing eight queens on an 8×8 chessboard such that none of them attack one another.
• The eight queen puzzle has 92 distinct solutions.
• If solution that differs only by symmetry operation of the board are counted as one puzzle has 12 unique solution.

Formulation of problem:

• States: any arrangement of 8 queens on board
• Initial state: 0 queens on the board
• Successor function: add a queen on any square
• Goal state: unattacked 8 queens on the board

Solution:

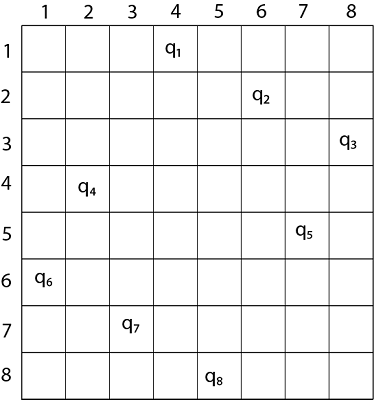
Steps to be perform:

1. Place the first queen in the left upper corner of the table
2. Save the attacked position
3. Move to the next queen which can only placed on next line
4. Search fopr a valid position.(unattackled position) If there is one go to step 8.
5. There is not a valid postion for a queen then delete it.
6. Move to the previous queen
7. Got o step 4
8. Place it to the first valid position
9. Save the attacked postions
10. If the queen processed is the last stop otherwise go to step 3.

Algorithm:      

PutQueen(row)

{

For every position col on the same row

If the position col is available

Place the next queen in position col

If(row<8)

PutQueen(row+1)

Else success

Remove the queen from positioncol

}

4.5 Sum of Subset

• In this problem there is given set with integer numbers and also some another values provided. We have to find a subset of given set whose sum is same as given sum value.
• Here backtracking is used for trying to select a valid subset when a number is not valid. We will backtrack to get the previous subset and add other number to get solution.
• In backtracking algorithm as we need to explore the nodes along gthe breadth and depth of tree.
• Generating nodes along breadth is controlled by loop and nodes along the depth are generated using recursion.
• This problem based on post order traversal method.
• Following are the steps to solve the problem:

Step 1: start with an empty set

Step 2: Add element from given list to the set

Step 3: If the set is having sum M then stop with that subset as solution

Step 4: if the set is not feasible then backtracks until we find the solution.

Step 5: If the set is feasible and sum of subset < M then go to step 2   

Step 6: if we have visited all numbers given in set without finding suitable solution and if no backtrack is possible then stop.

Example:

Given set of numbers= {1,3,2,4}

Find subsets with sum=3

Step 1: consider an empty set{ }

Add 1 into empty set { 1 } (sum=1,1<3)

Add 3 into set {1,3}  (sum=4,4>3,backtrack)

Remove 3 from subset { 1 }

Add 2 into set { 1,2 }  (sum=3,3=3,found solution)

We remove 2 and check all elements have been considered.

Solution:  { }  {1}  {1, 3}(backtrack) {1}  {1,2 }(found) {1}(end)

4.6 Graph ColoringAlgorithm

• In this problem we have given the graph and asked to color all vertices with n given colours in such a way that no two adjacent vertices should have the same colour. 
• The least possible value of n required to colour the graph successfully is known as the chromatic number of given graph.

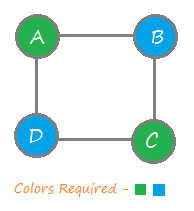
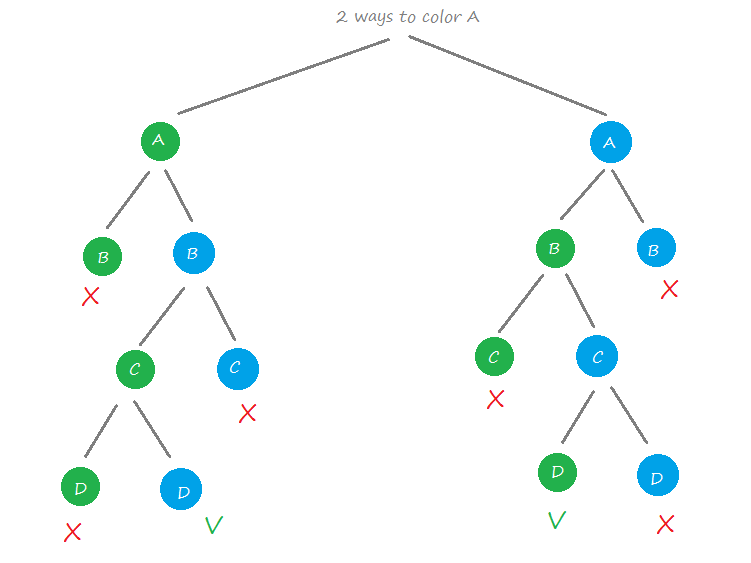
Steps to color graph:

Step 1: start with coloring single vertex

Step 2: move to its adjacent vertex and use that which is not used by its connecting vertex. If no color is available then backtracks ie. Un-color the last colored vertex and return false

Step 3: Repeat step 2 until all vertices of given graph are colored.

Step 4: if we find the vertex is uncoloured and its adjacent are colored with different colors and no color is available for current vertex then we need more colorsie. Bigger chromatic number.

Example:

4.7 Hamilton Cycle

Hamilton path is the path from first vertex to last vertex which visits each vertex exactly once in undirected or directed graph.

Hamilton cycle is the circuit in which there is an edge from the last vertex to first vertex.

In this problem we can determine whether graph contains a Hamilton cycle or not. If the cycle presents then it prints the cycle.

4.8 Knapsack Problem

• In 0/1 knapsack algorithm we have given set of items with weights and profit.
• The container of fixed capacity and are required to compute a loading of knapsack with items such that total profit is maximised.
• We have only 1 of each item hence there is either 0 or 1 of each item in the knapsack hence it is named as 0/1 knapsack problem.
• 0/1 knapsack problem can be solve efficiently using backtracking.

Example:

Let 4 items are given.

W=8

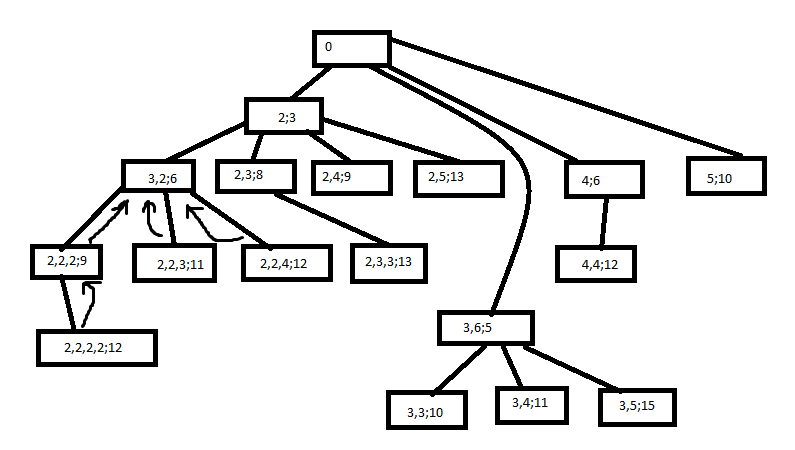
Selected weights are: 3 and 5

Maximum profit: 5+10=15

References

1. Thomas H Cormen and Charles E.L Leiserson, "Introduction to Algorithm" PHI, ISBN:81-203-2141-3

2. Anany Levitin,”Introduction to the Design & Analysis of Algorithm “,Pearson ISBN 81- 7758-835-4

3. Steven S Skiena, The Algorithm Design Manual, Springer,2nd edition, ISBN 978-81-8489-865-1

4. George T. Heineman, Gary Pollice, Stanley Selkow “Algorithms in a Nutshell, A Desktop Quick Reference”, O’Reilly, ISBN 13:978-81-8404-608-3