UNIT 6

COMPUTATIONAL COMPLEXITY & PARALLEL ALGORITHM

6.1 Deterministic Computation

• Deterministic computation is done with the Deterministic Turing Machine (DTM).
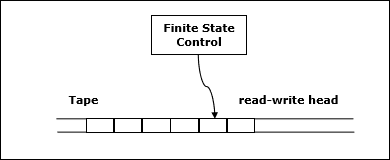
• This machine consists of finite state control, read write head and two-way tape with infinite sequence.
• The program for deterministic Turing machine having finite set of tape symbol, finite set of states, transition function.
• The P class solves the problem of deterministic computation.
• The problem can be solve by deterministic one tape Turing machine in polynomial time.

6.2 Non Deterministic Computation

• Another model of computation is non deterministic computation which works on Non-deterministic Turing Machine (NDTM).
• It is used to solve the computational problem.
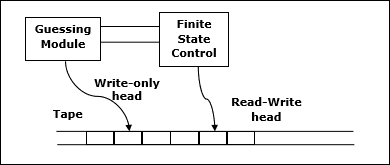
• The NDTM is much similar to DTM.
• It consists of one additional module i.e. guessing module which is one write-only head.
• The NP class solves the problem of non-deterministic computation.
• The problem can be solve by non-deterministic one tape Turing machine in polynomial time.

6.3 Polynomial Time Algorithm

• The algorithm which has input size n, if worst case time complexity of an algorithm is O(nK) where K is constant then it is called as polynomial time algorithm.
• Following are the polynomial run time algorithms:

1. Matrix chain multiplication
2. All pair shortest path
3. Single source shortest path
4. Minimum spanning tree, etc.

6.4 NP-Complete Class

• NP complete class is used to solve the problems of no polynomial time algorithm.
• If a polynomial time algorithm exists for any of these problems, all problems in NP would be polynomial time solvable. These problems are called NP-complete.
• The phenomenon of NP-completeness is important for both theoretical and practical reasons.
• Following are the no polynomial run time algorithm:

1. Hamiltonian cycles
2. Optimal graph coloring
3. Travelling salesman problem
4. Finding the longest path in graph, etc.

6.5 P Class

• The P class solves the problem of deterministic computation.
• P class is used to solve the problems that are solvable in polynomial run time.
• The problem belongs to class P if it’s easy to find a solution for the problem.
• These problem can be solved by worst case in O(nK) where k is constant.
• The problem which are solve by P class that are known as tractable problems and others are known as intractable or superpolynomial.
• If polynomial time is P(n) then algorithm can solve in time O (P(n)) with input size n.
• The advantage of class of polynomial time algorithm is that all reasonable deterministic single processor model of computation can be simulated on each other with at most polynomial slow-d.

6.6 NP-Class

• The NP class solves the problem of non-deterministic computation.
• The problem belongs to NP, if it’s easy to check a solution that may have been very tedious to find.
• It solves the problem which are verifiable by polynomial time.
• It is the class of decision problem.
• For using this class, it is easy to check the correctness of claimed answer even if it has extra information added in it.
• Hence it is used to verify the solution is correct not for finding the solution.
• If there is problem in this class then it can be solved by exhaustive search in exponential time.

6.7 NP Hard Class

• A problem is in the class NPC if it is in NP and is as hard as any problem in NP.
• A problem is NP-hard if all problems in NP are polynomial time reducible to it, even though it may not be in NP itself.
• The problem in NP-Hard cannot be solved in polynomial time, until P = NP.
• If a problem is proved to be NPC, there is no need to waste time on trying to find an efficient algorithm for it.
• Instead, we can focus on design approximation algorithm.
• Following are the NP hard class problems:

1. Circuit satisfiability problem
2. Set cover
3. Vertex cover
4. Travelling salesman problem

6.8 Application of NP complete class

6.8.1. Clique

• A clique is a complete sub graph which is made by given undirected graph.
• All the vertices are connected to each other i.e.one vertex of undirected graph is connected to all other vertices in graph.
• There is the computational problem in clique where we can find the maximum clique of graph this known as max clique.
• Max clique is used in many real world problems and in many application.
• Assume a social networking where peoples are the vertices and they all are connected to each other via mutual acquaintance that becomes edges in graph.
• In above example clique represents a subset of people who know each other.
• We can find max clique by taking one system which inspect all subsets.
• But the brute force search is too time consuming for network which has more than a few dozen vertices present in graph.

Example:

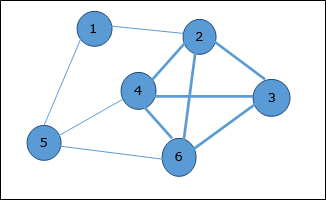
• Let take a example where 1, 2, 3, 4, 5, 6 are the vertices that are connected to each other in undirected graph.
• Here sub graph contains 2,3,4,6 vertices which forms a complete graph.
• Therefore sub graph is a clique.
• As this is a complete sub graph of given graph. So it’s a 4-clique.

Analysis of Clique Algorithm

• Non deterministic algorithm uses max clique algorithm to solve problem.
• In this algorithm we first find all the vertices in the given graph.
• Then we check the graph is complete or not i.e. all vertices should form a complete graph.
• The no polynomial time deterministic algorithm is used to solve this problem which is known as NP complete.

6.8.2. Vertex Cover

• A vertex-cover of an undirected graph G = (V, E) is a subset of vertices V' ⊆ V such that if edge (u, v) is an edge of G, then either u in V or v in V' or both.
• In given undirected graph we need to find maximum size of vertex cover.
• It is the optimization version of NP complete problem.
• It is easy to find vertex cover.

Example:

Given graph with set of edges are 

{(1,6),(1,2),(1,4),(2,3),(2,4),(6,7),(4,7),(7,8),(3,8),(3,5),(8,5)}

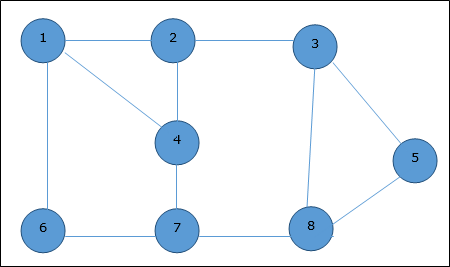
Now, start by selecting an edge (1, 6).

Eliminate all the edges, which are either incident to vertex 1 or 6 and we add edge (1, 6) to cover.

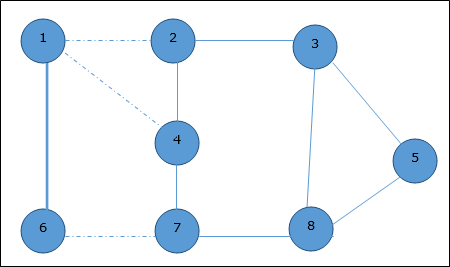
In the next step, we have chosen another edge (2, 3) at random

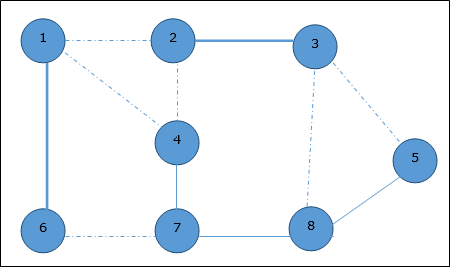
Now we select another edge (4, 7).

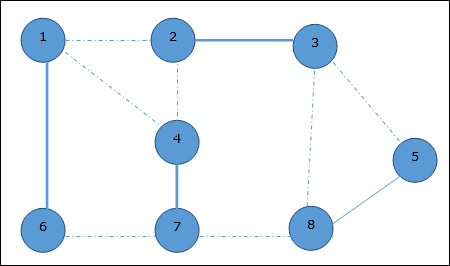
We select another edge (8, 5).

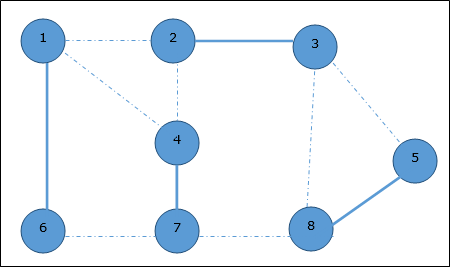
Hence, the vertex cover of this graph is {1, 2, 4, 5}.

Analysis of Vertex Cover Algorithm

• In this algorithm, by using adjacency list to represent E it is easy to see the running time of this algorithm is O (V+E).

6.9 Parallel Computing Algorithm

• It is related to concurrent computing.
• It is the computation process where execution of processes are carried out simultaneously.
• Large problems can be divided into smaller ones and which can be solved at same time.

6.10 Models of Parallel Computing

Following are the models of parallel computing:

1. PRAM(Parallel Random Access Machine)

It is good for complexity theory reasoning.

It is a abstract model.

It ignores many practical aspects i.e. only one person can write to certain memory location at a time

2.     CREW-PRAM (Concurrent-Read-Exclusive-Write-PRAM)

It ignores memory heterogeneity.

The processor write to a location at a time.

3.     Distributed memory

Each processor use its own local memory.

It cannot get local memory for another process.

It studies the properties of another processes network.

4.     BSP

It is known as Bulk-synchronous parallelism.

It uses distributed memory programming.

Using distributed memory programming, super steps in each step we can work on any local data and can send it to any other processor.

It is expensive to solve barriers in computing.

5.     Threaded programming

It uses shared memory i.e. every process can access all memory.

Here every independent computation can be done on independent thread.

It works on moderate scales i.e. limitation of shared memory.

It is difficult to handle interaction between threads.

6.     SIMD model

It is known as Graphics cards from NVidia.

It is a programming technique where each small piece of code can perform independently.

This model is restricted for some problems.

7.     Sequential semantics

It is a sequential program.

It operates on distributed objects.

It is tried on high performance but without much success.

The program is a sequential program, operating on distributed objects.

6.11 Pointer Doubling Algorithm

• It is also known as pointer jumping algorithm.
• Each of k processors are given a pointer to a unique element of a singly list of k items.
• It has each processor to learn its location in linked list.
• The processor with 16th element in the list should know that it is 16th in the list.

Algorithm for Pointer Doubling Algorithm:

For i= 1 to n-1 in parallel

Do

d[i]=1 d[n]=0

Repeat log n times

For each item i in parallel

If next[i] != nil then

d[i]=d[i] + d[next[i]]

Next[i]=next[next[i]]

• The code of this algorithm follows the following loop.
• The position of i equals d[i] + d[next[i]] + d[next[next[i]] + ...
• It solves the problem using parallel prefix problem.
• It finishes the work before recursion instead of after.
• To solve the parallel prefix problem we would replace the initialization for i= 1 to n-1 in parallel do d[i]=1 by for i= 1 to n-1 in parallel do d[i]=x[i].