Unit - 4
Cam and Follower
Types of cams
Cams are classified according to
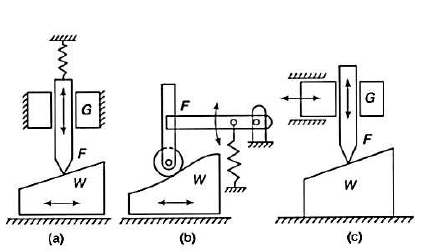
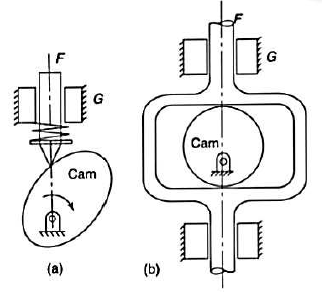
2. Radial or disc cams
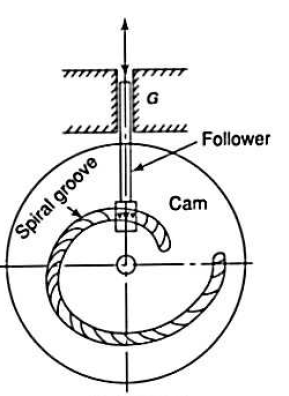
3. Spiral cams
4. Cylindrical cams
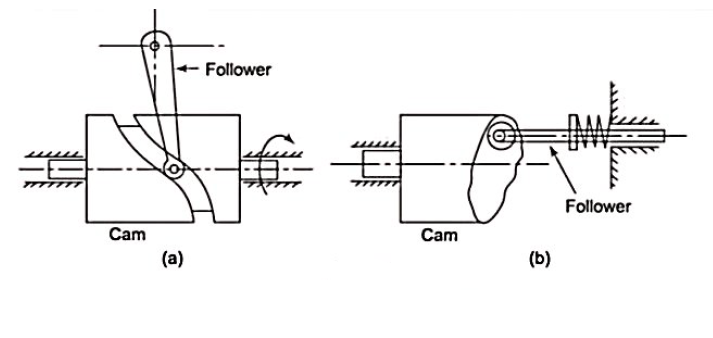
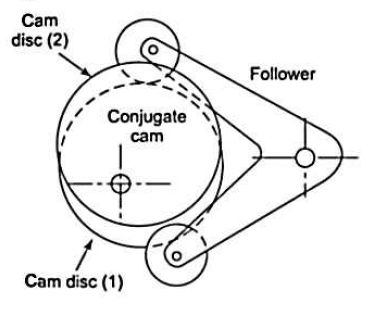
5. Conjugate cams:-
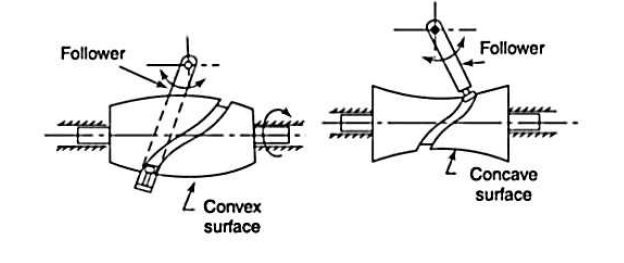
6. Globoidal cams
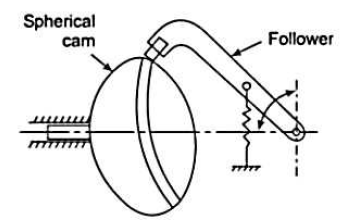
7. Spherical cams
b. According to follower movement
The motions of the followers are distinguished from each other by the dwells they have.
2. Dwell rise return dwell (D-R-R-D)
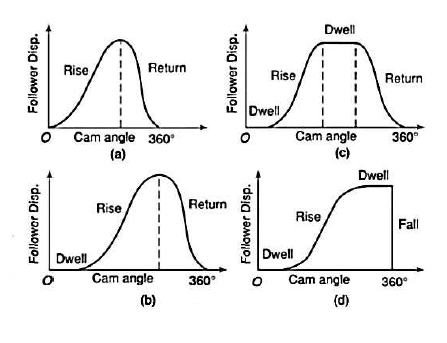
3. Dwell rise dwell return dwell (D-R-D-R-D)
Classification of followers
The followers may be classified as discussed below:
- Knife edge follower:
2. Roller follower:
3. Flat faced or mushroom follower:-
4. Spherical faced follower :-
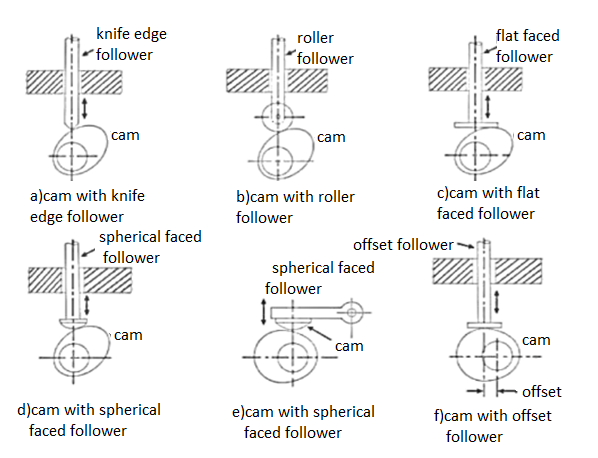
b. According to the motion of the follower the followers, according to its motion are of the following two types
2. Oscillating or rotating follower
c. According to the path of motion of the follower. The followers, according to its path of motion are of the following two types
2. Offset follower:-
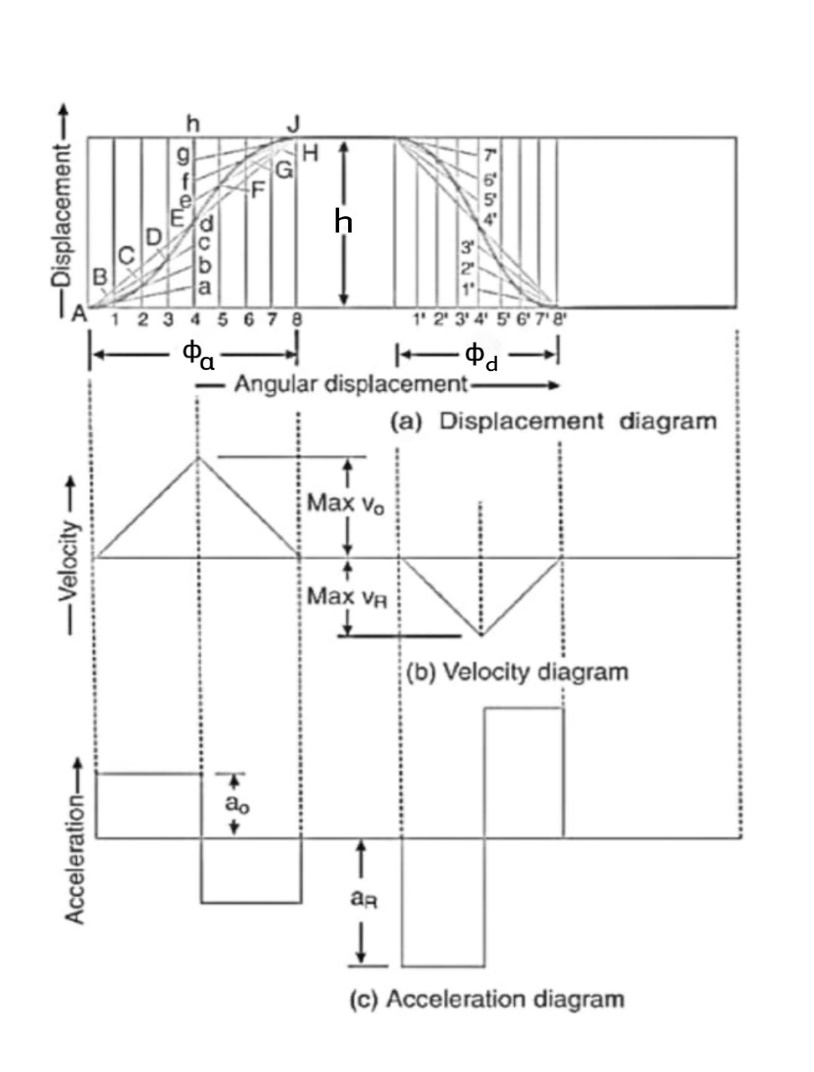
1. Displacement, velocity and acceleration diagrams when the follower moves with uniform velocity


2. Displacement, velocity and acceleration diagrams when the follower moves with simple harmonic motion

Let h =stroke of the follower,
 =angular displacement of the cam during out stroke and return stroke of the follower respectively, in radian, and
=angular displacement of the cam during out stroke and return stroke of the follower respectively, in radian, and
 = Angular velocity of the cam in radian/s
= Angular velocity of the cam in radian/s
Maximum velocity of the follower on the outstroke
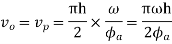
Maximum acceleration of the follower on the out stroke.

Similarly, maximum velocity of the follower on the return stroke.
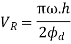
And maximum acceleration of the follower on the return stroke.
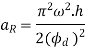
3. Displacement, velocity and acceleration diagrams when the follower moves with uniform acceleration and retardation
Let h=stroke of the follower.
 =angular displacement of the cam during out stroke and return stroke of the follower respectively, and
=angular displacement of the cam during out stroke and return stroke of the follower respectively, and
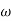 = Angular velocity of the cam.
= Angular velocity of the cam.
Maximum velocity of the follower during outstroke,

Similarly, maximum velocity of the following during return stroke,
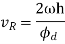


Maximum acceleration of the follower of during out stroke,
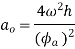
Similarly, maximum acceleration of the following during return stroke,
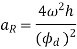
4. Displacement, velocity and acceleration diagrams when the follower moves with cycloidal motion
From a' draw a line parallel to AB intersecting the vertical lines through 1’ and 2’ at a and b respectively.
5. Similarly, from b’ draw a line parallel to AB intersecting the vertical lines through 4’ to 5’ at d & e respectively.
6. Join the point A a b c d e B by a smooth curve. This is the required cycloidal curve for the following during outstroke.

Let 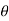 = angle through which the cam rotates in time t seconds, and
= angle through which the cam rotates in time t seconds, and
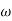 = Angular velocity of the cam.
= Angular velocity of the cam.
The velocity is maximum when
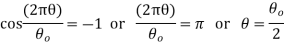
Maximum velocity of the following during outstroke,
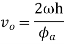
Similarly, maximum velocity of the following during return stroke,
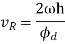
Maximum acceleration of the following due to out stroke,
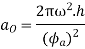
Similarly, maximum acceleration of the following during return stroke,
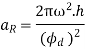
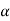
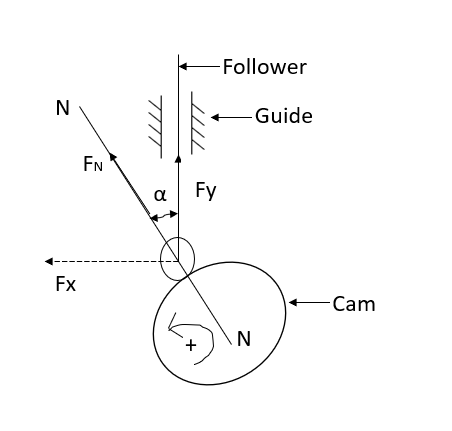

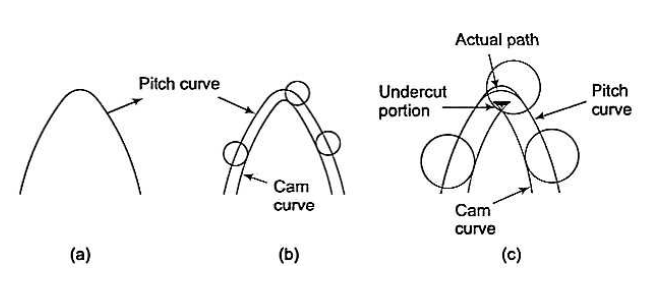
Undercutting
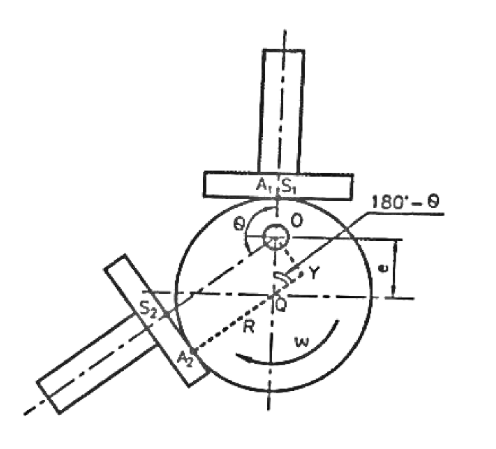
Lift of follower = y = 
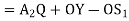
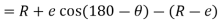
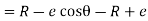
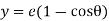
Differentiating equation with respect to time t we get
Velocity of follower = 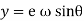
Differentiating equation with respect to time t, we get
Acceleration of follower=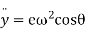
Where 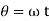 cam angle turned from lowest position
cam angle turned from lowest position
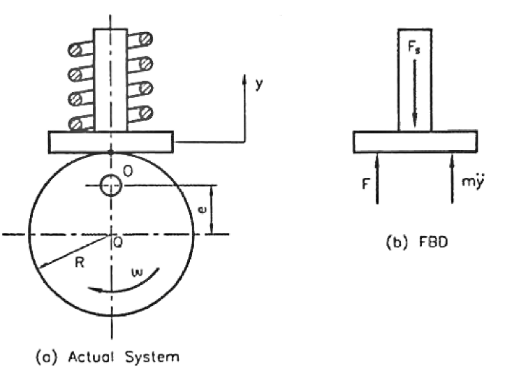
Let m=mass of follower
e=eccentricity
k = stiffness of spring
F = contact force between cam and follower
 = total spring force
= total spring force
P = preload in spring
 =Angular speed of cam
=Angular speed of cam
Then, from the free body diagram, we have
Inertia force = External forces
External forces
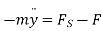

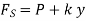
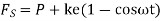

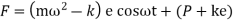
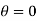
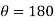
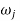
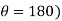
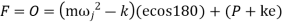
Where 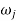 =jump speed
=jump speed
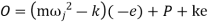
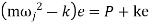

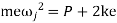
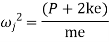
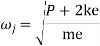
Therefore, to avoid jump
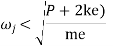
Or to avoid jump 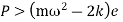
The 2-3 Polynomial D-R-D Cam
In this type of cam curves, four boundary conditions are used to hence displacement equation is given by,
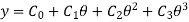 ……1
……1
Boundary condition are

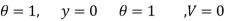
Differentiating the above equation w.r.t 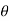 to get velocity of follower
to get velocity of follower

Initially put boundary conditions in equation (1),


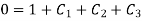
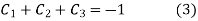
Now put the boundary conditions in equation (2)


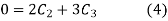
Put 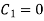 in equation (3)
in equation (3)
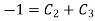 ……. 5
……. 5
Solving equation (4) and (5) we get
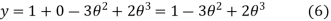
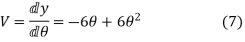
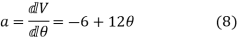

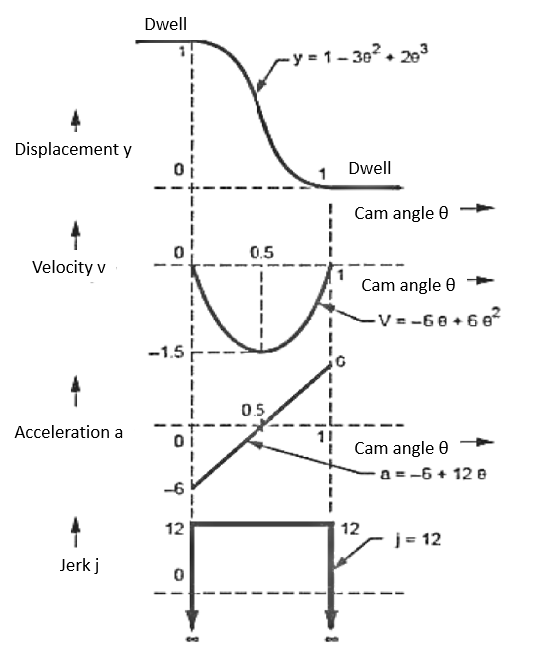
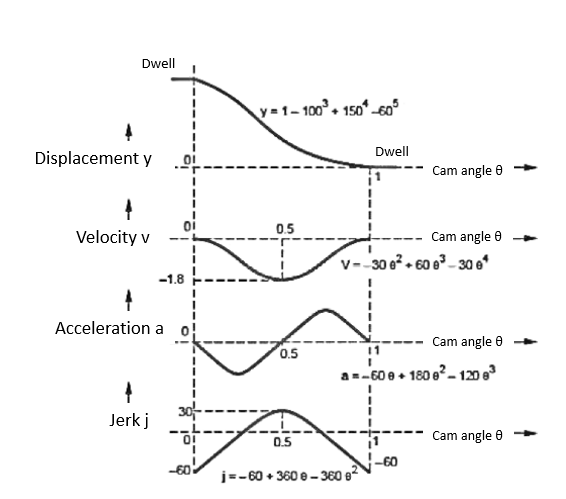
The 3-4-5 Polynomial D-R-D Cam
In this type of cam curves, six boundary conditions are used hence displacement equation is given by,
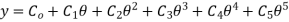 ……. 1
……. 1
Boundary conditions are
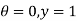
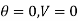
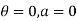
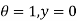
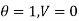
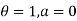
Differentiating the above equation w.r.t 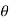 to get velocity follower,
to get velocity follower,

Again differentiating w.r.t. 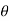 to get acceleration of follower,
to get acceleration of follower,
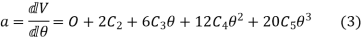
Initially put boundary conditions in equation (1)


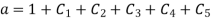
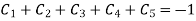 ……..(4)
……..(4)
Now put boundary condition in equation (2)

And 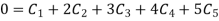
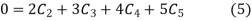
Now put boundary conditions in equation (3)

And 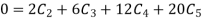
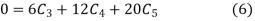
Put 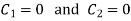 in equation (4) and (5)
in equation (4) and (5)
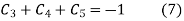

Solving equation (6),(7) and (8) we get
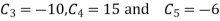
Substituting all these values in equation (1)
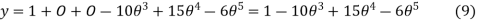
Velocity 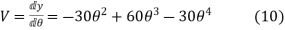
Acceleration 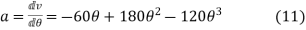
Jerk 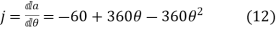
Numerical:
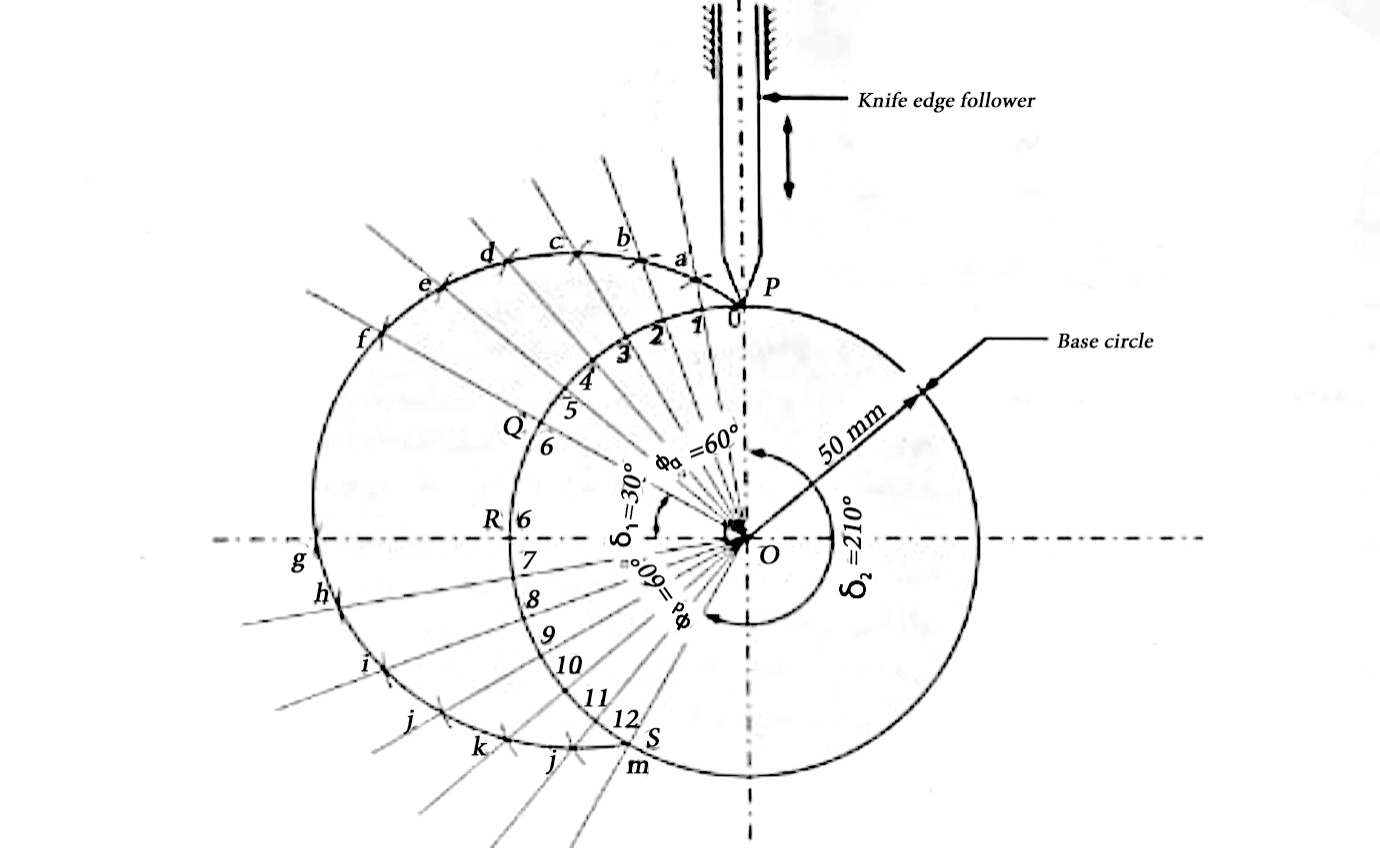
1. Cam is to give the following motion to a knife edge follower
The stroke of the follower is 40 mm and the minimum radius of the cam is 50mm. The follower moves the uniform velocity during both the out stroke and return stroke. Draw the profile of the cam, when the follower process through the axis of the camshaft.
Solution
Outstroke | Dwell | Return stroke | Remaining cam angle | Stroke in mm | Cam radius in mm |
600 | 300 | 600 | 2100 | 40 | 50 |
Procedure
Displacement diagram

Procedure to draw cam profile
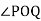
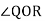
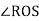
2. Draw the profile of a cam to raise a valve with SHM through 40 mm in 1/4th of revolution keep it fully raised through 1/10th of revolution and to lower it with uniform acceleration and retardation in 1/6th of revolution. The valve remains closed during rest of the revolution. The diameter of roller is 20mm and minimum radius of CAM to be 30mm. Axis of the valve road passes through the axis of cam shaft.
Solution:
Outstroke =1/4th of revolution=1/4 ×360=900
Dwell=1/10th of revolution=1/10×360=360
Return stroke=1/6th of revolution=1/6×360=600
Outstroke | Dwell | Return stroke | Remaining cam angle | Stroke in mm | Cam radius in mm | Diameter of roller in mm | Radius of roller in mm | Prime circle radius in mm |
90° | 36° | 60° | 174° | 40 | 30 | 20 | 10 | 40 |
Prime circle radius is calculated by adding the radius of roller to the radius of base circle/cam radius
Procedure:
Displacement diagram
Procedure to draw cam profile:

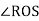
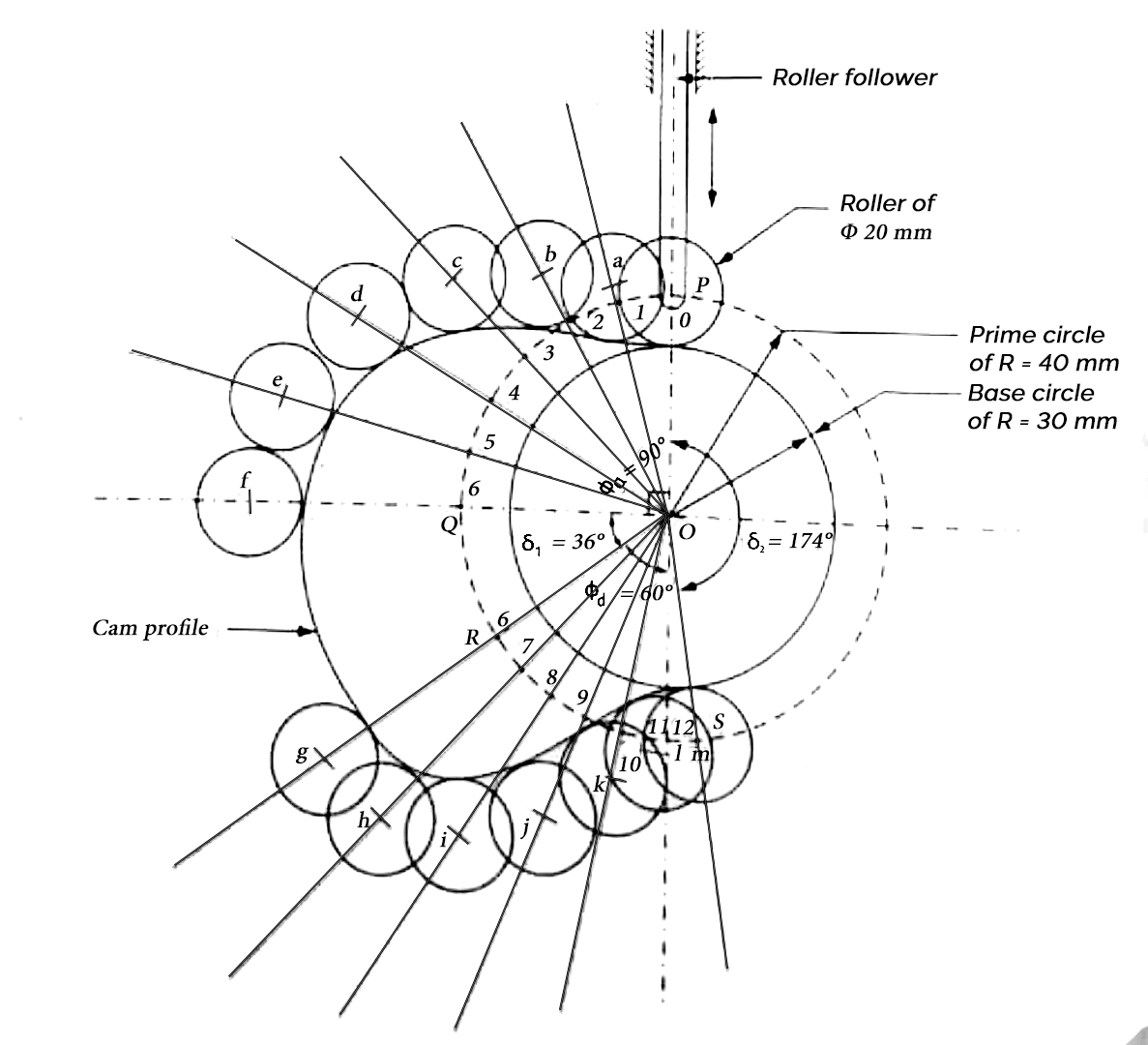
3. A flat faced mushroom follower is operated by a uniformly rotating cam. The follower is raised through a distance of 25mm in 120° rotation of the cam, remains at rest for the next 30 degree and is lowered during further 120-degree rotation of the cam. The raising of the following takes place with cycloidal motion and the lowering with uniform acceleration and deceleration. However, the uniform acceleration is 2/3 of the uniform deceleration. The least radius of the cam is 25mm which rotates at 300rpm. Draw the cam profile and determine the values of the maximum velocity and maximum acceleration during rising, and maximum velocity and uniform acceleration and deceleration during lowering of the follower.
Solution:
h=25mm 
During the return stroke, as the uniform acceleration is 2/3 of the uniform deceleration, the uniform deceleration is 3/2 of the uniform acceleration.
Let the uniform acceleration be f so that the uniform deceleration be (3/2)f.
Time of acceleration
Final velocity,
v=u +ft=ft ……. Initial velocity = 0
Or 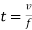
Time of deceleration
Initial velocity is v and final velocity zero.
Therefore
0=v - (3/2) f t'
Where t’ is the time of deceleration and negative sign due to declaration.
The time of deceleration is 2/3 of the time of acceleration.
Displacement
During acceleration 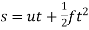

During deceleration=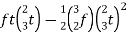
[As initial velocity f t and time taken 2/3t]
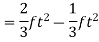
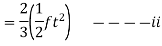
Comparison of i and ii shows that the distance travelled during deceleration period is 2/3 of the distance travel during acceleration.
The displacement diagram has been shown in figure a. During the return stroke, the time of acceleration and the displacement are 3/2 times of the corresponding values during the deceleration. Thus, the time of acceleration is 3/5 of the total time of return and the displacement is 3/5 of the total displacement.
To draw the cam profile, proceed as follows:

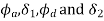
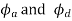
During ascent


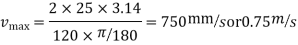
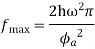
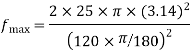

During descent
v=f t
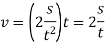
v will the maximum at the end of acceleration period.
At the end of the acceleration period,
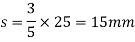
And the time taken to travel this distance is found as under,
Time for 300rev.=60s
Time for 1 rev =60/300 =0.2sec.
Time for 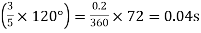
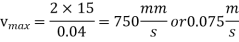
Uniform acceleration

Uniform deceleration
=18.75×3/2 =28.13 
4. The following data related to a cam operating and oscillating roller follower:
Minimum radius of cam=44mm
Diameter of roller=14mm
Length of the follower arm=40mm
Distance of fulcrum centre from cam centre=50mm
Angle of ascent=75°
Angle of decent=105°
Angle of Dwell for follower in the highest position=60°
Angle of oscillation of follower=28°
Draw the profile of the cam if the ascent and decent both take place with SHM.
Solution: 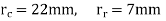

Follower arm length =40mm
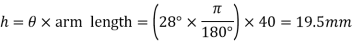
The displacement diagram has been shown in figure a .
To draw the cam profile, proceed as follows:
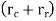
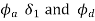
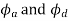
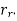
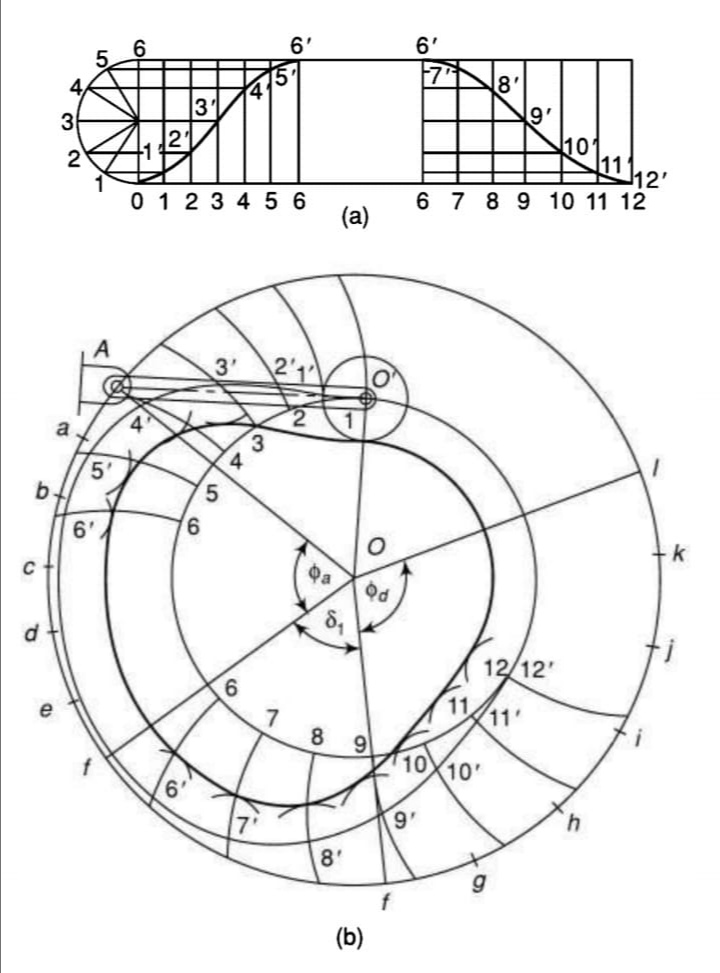
5. The following data is related to a cam profile, in which the follower moves with SHM during the lift and returning it with acceleration and deceleration , acceleration being half the deceleration.
Minimum radius of cam=30mm
Roller radius =10mm
Lift of follower =45mm
Offset of follower axis=12mm
Angle of ascent =700
Angle of descent=1200
Angle of dwell between ascent and descent=450
Speed of cam=300rpm
Draw the cam profile and determine maximum velocity, maximum acceleration during lift.
Solution Given data
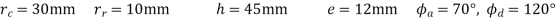
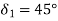
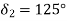
N=300rpm 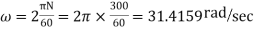
It is given that, during return stroke nature of follower motion is uniform acceleration and retardation but acceleration period is half of the deceleration period,
Let 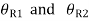 be the angle of acceleration and retardation respectively,
be the angle of acceleration and retardation respectively,

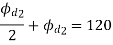

Similarly, 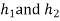 be the displacement of follower during acceleration and retardation period.
be the displacement of follower during acceleration and retardation period.
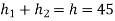
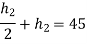
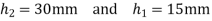
The displacement diagram has been shown in figure a.
To draw the cam profile, proceed as follows:
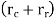
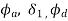
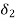
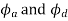
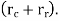

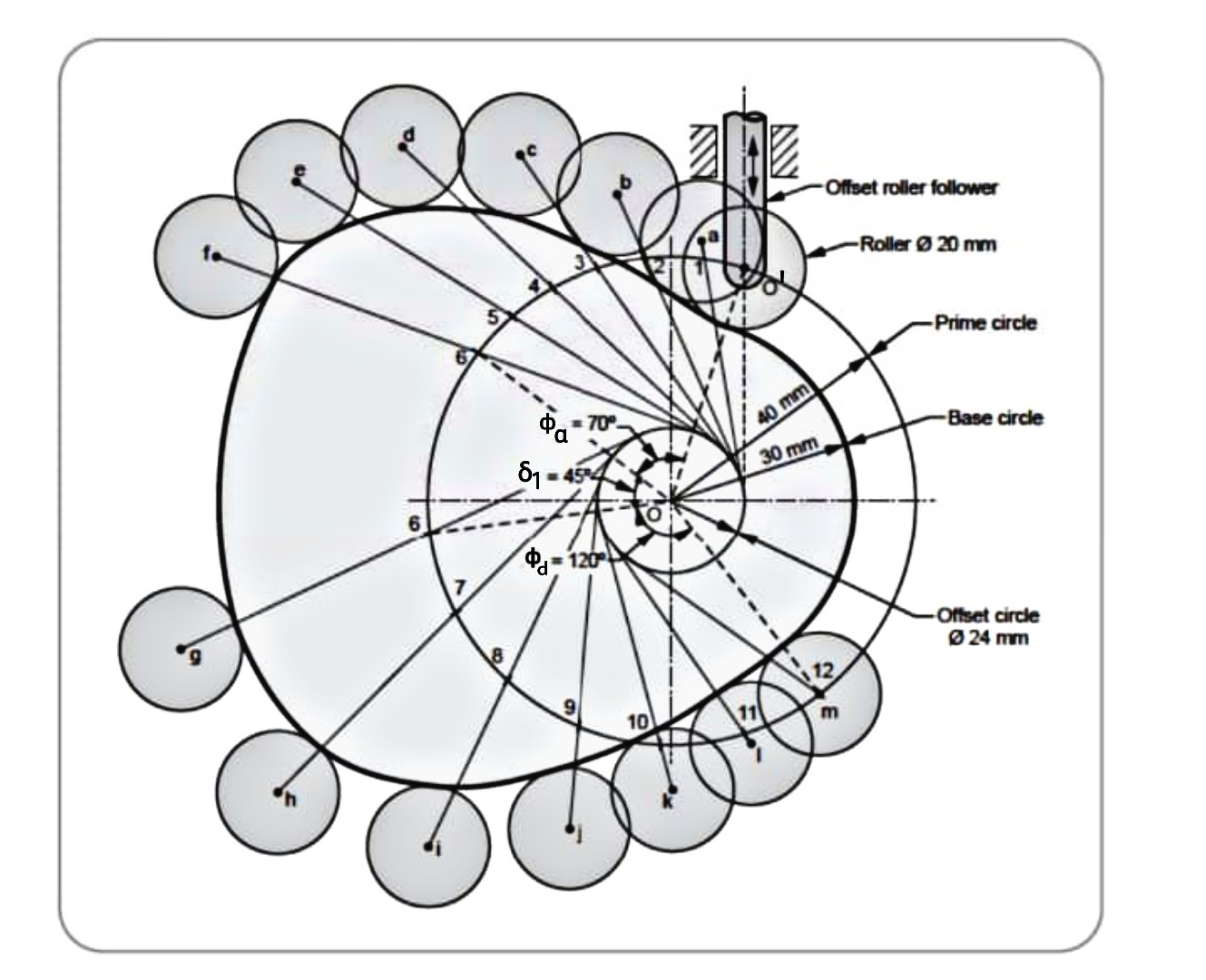
Maximum velocity of follower during lift is
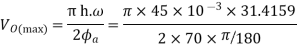
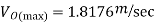
Maximum acceleration of follower during lift is
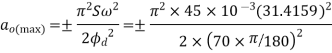
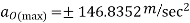
6. An eccentric cam of eccentricity 3.75cm drives a follower of mass 1.75Kg. The spring holding the follower against the cam has stiffness of 24 N/mm and has initial compression of 3.125 cm. It is observed that jump occurs at cam rotation 1000 from the lowest position of the cam. Find out the speed of cam. Find out the speed of cam in r.p.m. Also find out maximum usable speed of cam without jump.
Solution Given that :
e =3.75cm =0.0375m m=1.75Kg K=24N/mm =24*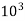 N/m
N/m
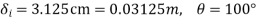
To find i) Cam speed (N) ii) Limiting speed
Step-I Calculate the speed of cam
Preload in the spring is,
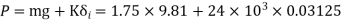
P=767.1675N
Contact force between cam and follower is
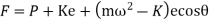
But jump will occur when F=0
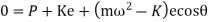
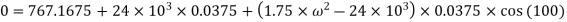
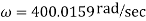
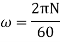
N=3819.8704 rpm
This is the speed at which jump will occur.
To avoid cam jump limiting speed is,
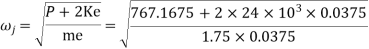
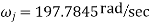
Now 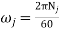
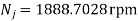
It means to avoid cam jump; the cam speed should be less than or equal to limiting speed i.e. 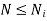
1. Ghosh Malik, Theory of Mechanism and Machines, East-West Pvt. Ltd.
2. Hannah and Stephans, Mechanics of Machines, Edward Arnolde Publication.
3. R L Norton, Kinematics and Dynamics of Machinery, First Edition, McGraw Hill Education
(India) P Ltd. New Delhi
4. Sadhu Singh, Theory of Machines, Pearson
5. D.K. Pal, S.K. Basu, Design of Machine Tools, Oxford & Ibh Publishing Co Pvt. Ltd.
6. Dr. V. P. Singh, Theory of Machine, Dhanpatrai and sons.
7. C. S. Sharma & Kamlesh Purohit, “Theory of Machine and Mechanism”, PHI.