Unit – 5
Synthesis of Mechanism
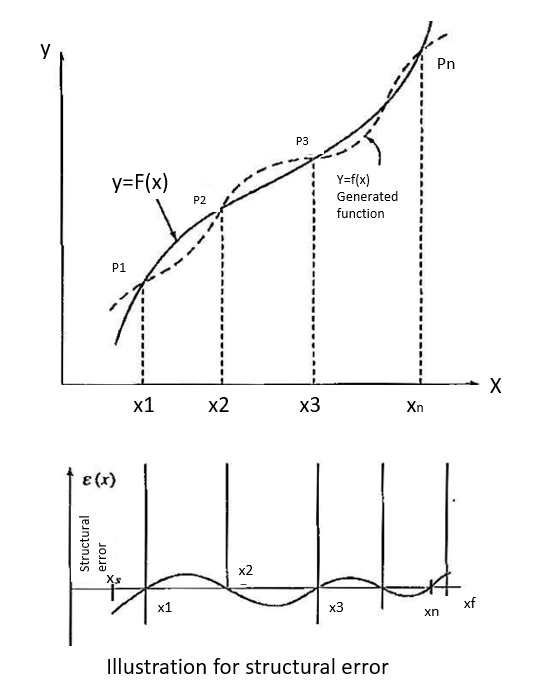
Kinematics synthesis
Synthesis process may be accomplished, in general, in three interrelated faces:
1. Type synthesis
2. Number synthesis
3. Dimensional synthesis
1. Path generation
2. Function generation
3. Motion generation
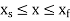
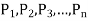
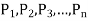


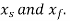
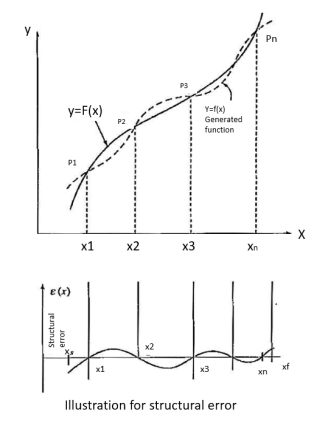
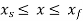
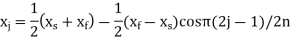
Where 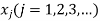 are the accuracy points. Thus, for first, second, and third accuracy points, j is equal to 1,2, and 3 respectively.
are the accuracy points. Thus, for first, second, and third accuracy points, j is equal to 1,2, and 3 respectively.
n = total number of accuracy points.
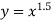
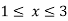
Here. 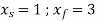
And n= number of accuracy points=3
First, second and third accuracy points are
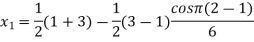
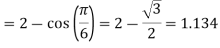
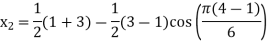
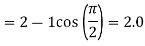
And 
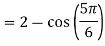
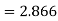
Corresponding values of the dependent variable by, as obtained by substituting 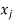 values (j=1,2,3) in the function
values (j=1,2,3) in the function 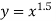
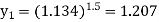
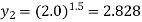
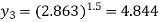
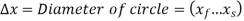
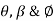

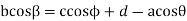
Squaring both sides
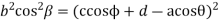
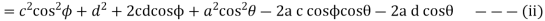
Now taking the sum of the components along y-axis we have
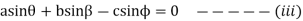

Squaring both sides
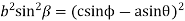
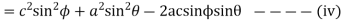
Adding equations (ii) and (iv)
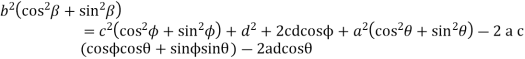

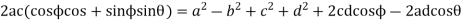
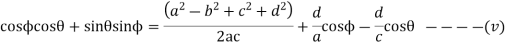
Let 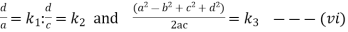
Equation (v) can be written as
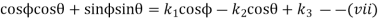
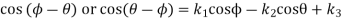
The equation (vii) is known as the Freudenstein equation.
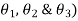
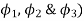
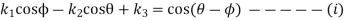
Where 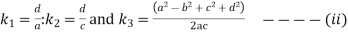
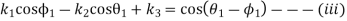
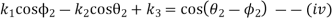

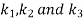
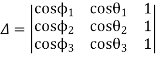
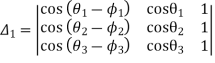
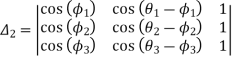
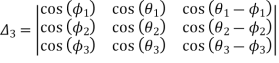
Now the values of 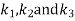 are given by
are given by
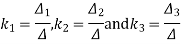
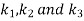
Numericals
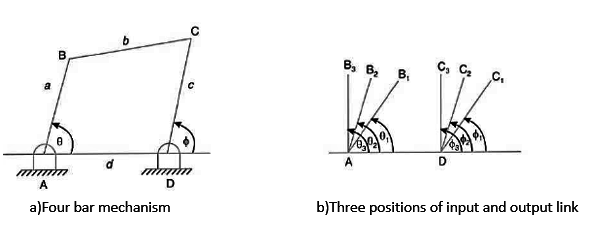
1. Synthesize a four-bar linkage as shown in Fig using Freudenstein’s equation to satisfy in one of its positions. The specification of position  velocity
velocity  and accelerations
and accelerations  are as follows:
are as follows:
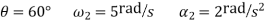

Given 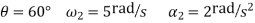
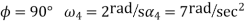
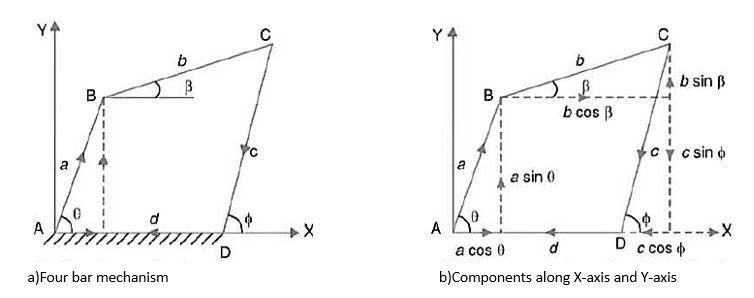
The four-bar linkage is shown in Figure Let
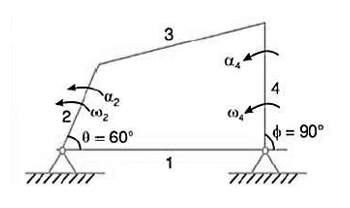
AB = Input Link=a
BC=Coupler=b
CD=Output link =c and
AD=Fixed link =d
The Freudenstein’s equation is given by
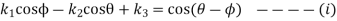
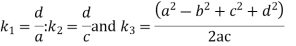
Substituting the value of  in equation (i)
in equation (i)

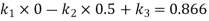
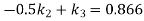

Differentiating equation (i) with respect to time
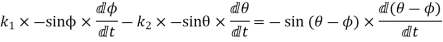
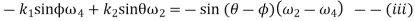
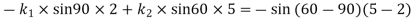
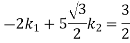
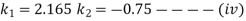
Now differentiating equation(iii) with respect to time
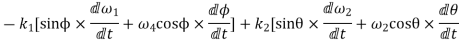
= - 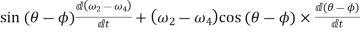
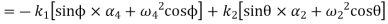
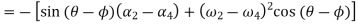

=-[sin(60-90)(2-7)+(5-2)2 cos(60-90)]
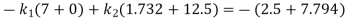

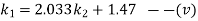
From equation (iv) and (v)
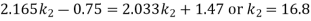
From equation (v)
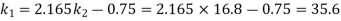
And from equation (ii)

Assuming the length of one of the links say an as one unit we get the length of the links as follows
We know that
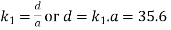 units
units
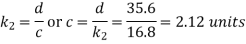
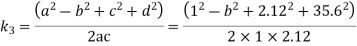

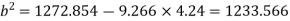
b=35.12 units
2. Synthesize a four-bar mechanism to generate a function y = sinx for 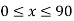 . The range of the output crank may be chosen as 60 while that of input crank be 1200. Assume three precision points which are to be obtained from Chebyshev spacing. Assume fixed link to be 52.5mm long and
. The range of the output crank may be chosen as 60 while that of input crank be 1200. Assume three precision points which are to be obtained from Chebyshev spacing. Assume fixed link to be 52.5mm long and 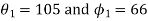
Solution Given 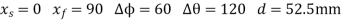

The three values of x corresponding to three precision points according to Chebyshev spacing are given by
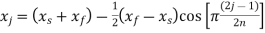 where j=1,2,3
where j=1,2,3
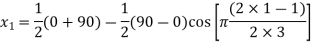
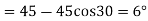
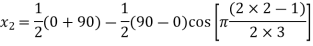
=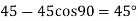
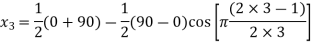
=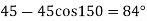
Since y = sinx, therefore corresponding values of y are

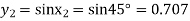
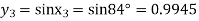
Also 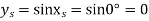
And 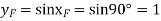
The relation between the input angle 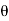 and x is given by
and x is given by
 where j=1,2,3
where j=1,2,3
The above expression may be written as
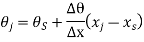
The three values of  corresponding to three precision points are given by
corresponding to three precision points are given by
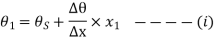
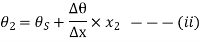
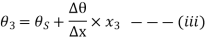
From equations (i) (ii) and (iii)
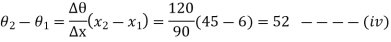

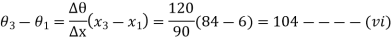
Since 

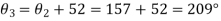
The relation between the output angle and y is given by
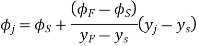
The expression may be written as
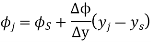
The three values of 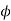 corresponding to three precision points are given by
corresponding to three precision points are given by
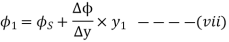
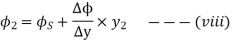

From equations (vii),(viii) and (ix)

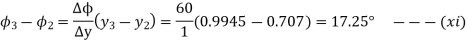

Since  therefore
therefore

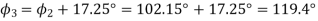
We have calculated above the three positions.
Let a=Length of the input crank
b=Length of the coupler
c=Length of the output crank, and
d= Length of the fixed crank=52.5mm
We know that Freudenstein displacement equation is
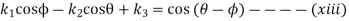
Where 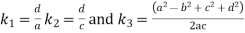
The equation (xiii) for the first position of input and output crank may be written as
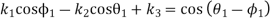
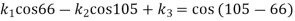
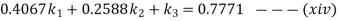
Similarly, for the second position
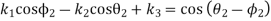
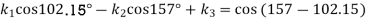
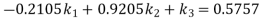
And for the third position (when 
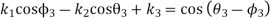
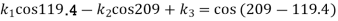
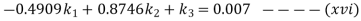
Solving the three simultaneous equations (xiv), (xv) and (xvi) we get
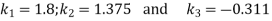
Since the length of the fixed link (i.e. d=52.5mm) is known therefore we get the length of other links as follows:
We know that
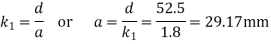
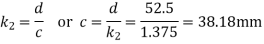
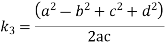
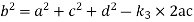
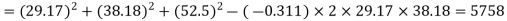
b=75.88mm
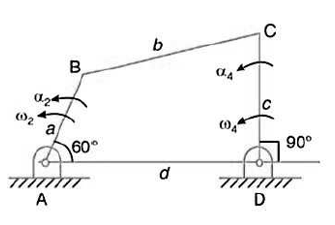
3. Design a slider-crank mechanism to co-ordinate three positions of the input link and the slider for the following angular and linear displacement of the input link and the slider respectively,


Solution The required slider-crank mechanism can be designed as follows:

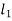
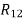
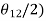
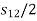
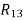
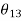
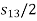

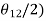
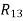

Then, ABC is the required slider-crank mechanism. The figure shows the same in three positions.
(a)
(b)
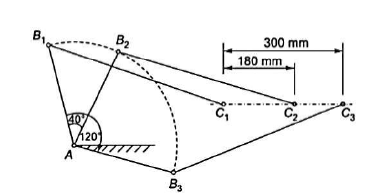
4. Design a slider-crank mechanism to co-ordinate three positions of the input and the slider for the following data by inversion method
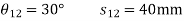

Eccentricity = 20 mm.
For the given to angular displacement of the input link and the two linear displacements of the slider along with the eccentricity e, the required slider-crank mechanism is obtained as follows:
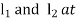
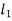

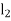
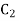
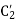
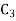

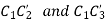
Then 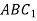 is the required slider-crank mechanism. Figure b shows the mechanism in the required three positions.
is the required slider-crank mechanism. Figure b shows the mechanism in the required three positions.
(a)
(b)
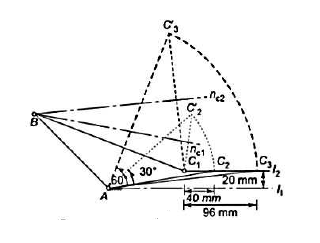
5. Design of four-link mechanism to co-ordinate four positions of the input and output links for the following angular displacement of the input link and the output link respectively:



Solution. Make the following construction:
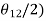
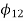
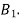
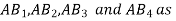
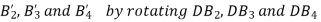
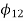
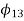
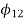
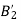
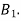
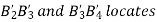
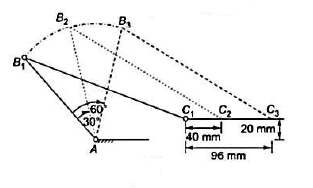
(a)
(b)
6. A four-bar mechanism is to be designed by using three precision points to generate the function
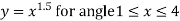
Assuming 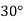 starting position and
starting position and 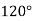 finishing position for the input link and
finishing position for the input link and 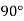 starting position and
starting position and 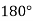 finishing position for the output link, find the values of x, y,
finishing position for the output link, find the values of x, y, 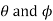 corresponding to the three precision points.
corresponding to the three precision points.
Given 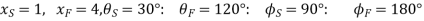
Values of x
The three values of x corresponding to three precision points according to Chebyshev’s spacing are given by:
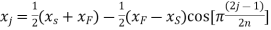 where j=1,2 and 3
where j=1,2 and 3
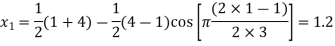
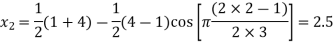
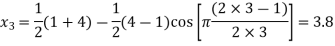
Values of y
Since 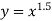 therefore the corresponding values of y are
therefore the corresponding values of y are

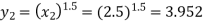
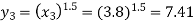
Values of 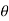
The three values of  corresponding to three precision points are given by
corresponding to three precision points are given by
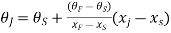 , where j=1,2,3
, where j=1,2,3
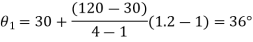
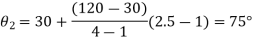
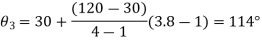
Value of 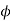
The three values of 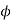 corresponding to three precision points are given by
corresponding to three precision points are given by
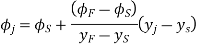
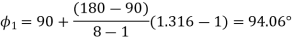
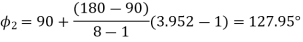
Reference:
1. Ghosh Malik, Theory of Mechanism and Machines, East-West Pvt. Ltd.
2. Hannah and Stephans, Mechanics of Machines, Edward Arnolde Publication.
3. R L Norton, Kinematics and Dynamics of Machinery, First Edition, McGraw Hill Education
(India) P Ltd. New Delhi
4. Sadhu Singh, Theory of Machines, Pearson
5. D.K. Pal, S.K. Basu, Design of Machine Tools, Oxford & Ibh Publishing Co Pvt. Ltd.
6. Dr. V. P. Singh, Theory of Machine, Dhanpatrai, and sons.
7. C. S. Sharma & Kamlesh Purohit, “Theory of Machine and Mechanism”, PHI.