UNIT 1
Elementary Ideas of Arithmetic Progression
Arithmetic Progression Define
An A.P. Is referred as a sequence in which terms increase or decrease by a fixed number referred as common difference of the A.P.
AP. Sequence is expressed as a, a + d, a + 2d, …..
a: first term, d: common difference
Nth Term formula
an = a + (n-1)d
an: nth term, n: number of terms
Sn Sum of the 1st n terms
Sn = n/2(2a+(n-1)d) = n/2 (a + l)
l= last term
To each term of a given A.P. a fixed number is added or subtracted or multiplied or divided the resulting sequence is an AP with a common difference d.
Consider 2 AP’s a1, a2, a3….. And b1, b2, b3….. With common differences d and d’ respectively then a1+b1, a2+b2, a3+b3…. Is also an A.P. With common difference d + d’
General combination of 3 terms in an A.P. a – d, a, a + d.
General combination of 4 terms in an A.P. a – 3d, a – d, a + d, a + 3d.
In case a1, a2, a3,…… an are in A.P. Then relation will be a1 + an = a2 + an-1 = a3 + an-2 = ……
If nth term of a sequence is a linear expression in n, the sequence will be an AP; its common difference will be coefficient of n.
In case sum of n terms of a sequence is a quadratic in n, its constant term is zero, the sequence will be an AP, its common difference is twice the coefficient of n2. If constant term is non-zero, it will be an .A.P. From 2nd term onwards.
Example 1
Find the value of n. If a = 10, d = 5, an = 95.
Solution
Given, a = 10, d = 5, an = 95
From the formula of general term, we have:
an = a + (n − 1) × d
95 = 10 + (n − 1) × 5
(n − 1) × 5 = 95 – 10 = 85
(n − 1) = 85/ 5
(n − 1) = 17
n = 17 + 1
n = 18
Example 2
Find the 20th term for the given AP:3, 5, 7, 9, ……
Solution: Given,
3, 5, 7, 9, ……
a = 3, d = 5 – 3 = 2, n = 20
an = a + (n − 1) × d
a20 = 3 + (20 − 1) × 2
a20 = 3 + 38
⇒a20 = 41
Example 3:
Find the sum of first 30 multiples of 4.
Solution: Given, a = 4, n = 30, d = 4
We know,
S = n/2 [2a + (n − 1) × d]
S = 30/2[2 (4) + (30 − 1) × 4]
S = 15[8 + 116]
S = 1860
Example 4 –
How many terms are added in 24+20+16+ ....... 10 make the sum 72.
Solution
We know that sum to first n terms of an A.P. = Sn = n/2 [2a + (n – l) d]
Let the sum of n terms be 72, a = 24, d = -4
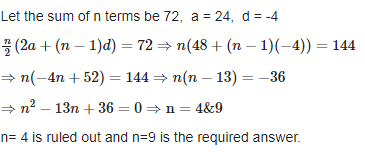
Key takeaways –
- The behavior of the arithmetic sequence depends on the common difference .
Geometric Progression
G.P. Is a sequence its 1st term is non-zero and its succeeding terms is r times the previous term, r is a fixed non-zero number called as the common ratio of the G.P.
Nth Term and Sum of n Terms:
‘a’ : 1st term, ‘r’ : common ratio
G.P. Is a, ar, ar2, …..
Nth Term ‘an’ is specified as an = arn-1
Sum Sn of the 1st n terms of the G.P. Is
Sn = [a(rn -1)]/(r-1) ; r ≠1
= na, r =1
Consider -1< r <1,
Sum of the infinite G.P. Is
a + ar + ar2 + ……= a/(1-r).
In case each term of a G.P. Is multiplied by a fixed non-zero constant, the resulting sequence is a G.P. With a common ratio.
If each term of a G.P. Is increased to the power k, the resulting sequence will be a G.P. With common ratio rk.
a1, a2, a3…… is a G.P. With common ratio r.
b1, b2, b3…… is a G.P. With common ratio r’.
The sequence will be a1b1, a2b2, a3b3 is a G.P. With common ratio rr’.
Consider 3 terms in G.P. As a/r, a, ar. In case we have to take (2k+1) terms in a
G.P. We take a/rk, a/rk-1, a, ar, ark
For 4 terms in a G.P. We take a/r3, a/r, ar, ar3. For 2k terms in a G.P. We take
a/r2k-1, a/r2k-3, ……., a/r, ar, ….ar2k-1
If a1, a2,…..,an are in G.P. Then a1 an = a2 an-1 = a3 an-2 = …..
If a1, a2, a3, ………. Is a G.P. Then loga1, loga2, loga3…… is an AP. The converse is also true.
If {tn} is a G.P. Then the common ratio r = (tp/tq)1/p-q
Harmonic Progression (H.P.)
If the sequence 1/a1, 1/a2, 1/a3, …..1/an, ……, is an AP then the sequence a1, a2, a3……an….
(ai ≠ 0) is said to be an H.P.
Nth Term of H.P.
Sum of n terms,
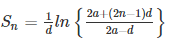
Where,
“a” is the first term of A.P
“d” is the common difference of A.P
“ln” is the natural logarithm
Examples 1
If the first term is 10 and the common ratio of a GP is 3. Then write the first five terms of GP.
Solution: Given,
First term, a = 10
Common ratio, r = 3
We know the general form of GP for first five terms is given by:
a, ar, ar2, ar3, ar4
a = 10
Ar = 10 x 3 = 30
Ar2 = 10 x 32 = 10 x 9 = 90
Ar3 = 10 x 33 = 270
Ar4 = 10 x 34 = 810
Therefore, the first five terms of GP with 10 as first term and 3 as common ratio is:
10, 30, 90, 270 and 810
Examples 2
The sum of three numbers in a GP is 26 and their product is 216. Ind the numbers.
Solution : Let the numbers be a/r, a, ar.
=> (a / r) + a + a r = 26
=> a (1 + r + r2) / r = 26
Also, it is given that product = 216
=> (a / r) x (a) x (a r) = 216
=> a3 = 216
=> a = 6
=> 6 (1 + r + r2) / r = 26
=> (1 + r + r2) / r = 26 / 6 = 13 / 3
=> 3 + 3 r + 3 r2 = 13 r
=> 3 r2 – 10 r + 3 = 0
=> (r – 3) (r – (1 / 3) ) = 0
=> r = 3 or r = 1 / 3
Thus, the required numbers are 2, 6 and 18.
Examples 3
Find the number of terms in the geometric progression 6, 12, 24, ..., 1536
Solution
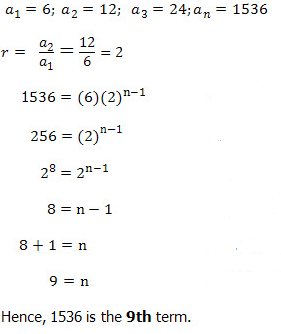
Examples 4
Determine the 4th and 8th term of the harmonic progression 6, 4, 3,…
Solution:
Given:
H.P = 6, 4, 3
Now, let us take the arithmetic progression from the given H.P
A.P = ⅙, ¼, ⅓, ….
Here, T2 -T1 = T3 -T2 = 1/12 = d
So, in order to find the 4th term of an A. P, use the formula,
The nth term of an A.P = a+(n-1)d
Here, a = ⅙, d= 1/12
Now, we have to find the 4th term.
So, take n=4
Now put the values in the formula.
4th term of an A.P = (⅙) +(4-1)(1/12)
= (⅙)+(3/12)
= (⅙)+ (¼)
= 5/12
Similarly,
8th term of an A.P = (⅙) +(8-1)(1/12)
= (⅙)+(7/12)
= 9/12
Since H.P is the reciprocal of an A.P, we can write the values as:
4th term of an H.P = 1/4th term of an A.P = 12/5
8th term of an H.P = 1/8th term of an A.P = 12/9 = 4/3
Examples 5
Compute the 16th term of HP if the 6th and 11th term of HP are 10 and 18 respectively.
Solution:
The H.P is written in terms of A.P are given below:
6th term of A.P = a+5d = 1/10 —- (1)
11th term of A.P = a+10d = 1/18 ……(2)
By solving these two equations, we get
a =13/90, and d = -2/ 225
To find 16th term, we can write the expression in the form,
a+15d = (13/90) – (2/15) = 1/90
Thus, the 16th term of an H.P = 1/16th term of an A.P = 90
Therefore, the 16th term of the H.P is 90.
Key takeaways –
- Geometric Progression refers to the numbers taken in a specific order. Harmonic progression is the reciprocal of arithmetic progression
Permutation and combination are very important concept in mathematics. It represent a group of objects by selecting them in a set and forming subsets. It defines the various ways to arrange a certain group of data. Permutations refers to when we select the data or objects from a certain group, whereas the order in which they are represented is called combination.
Permutation
In mathematics, permutation relates to the act of arranging all the members of a set into some sequence or order. Permutations occur, in more or less prominent ways, in almost every area of mathematics. They often arise when different orderings on certain finite sets are considered.
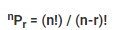
Combination
The combination is a way of selecting items from a collection, such that (unlike permutations) the order of selection does not matter. Combination refers to the combination of n things taken k at a time without repetition.
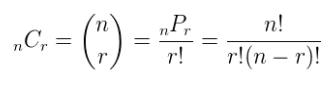
Example 1
Find the number of permutations and combinations if n = 12 and r = 2.
Solution:
Given,
n = 12
r = 2
Using the formula given above:
Permutation:
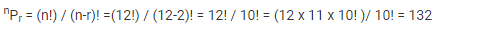
Combination:
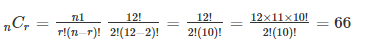
Key takeaways –
- The study of permutations and combinations is concerned with determining the number of different ways of arranging and selecting objects out of a given number of objects, without actually listing them.
The Binomial Theorem is the method of expanding an expression which has been raised to any finite power. A binomial Theorem is a powerful tool of expansion, which has application in Algebra, probability, etc.
Let n ∈N,x,y,∈ R then
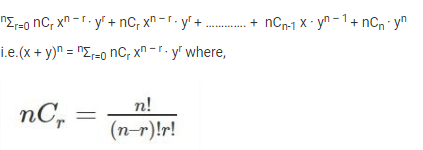
General term in binominal expansion
We have (x + y)n = nC0 xn + nC1 xn-1 . y + nC2 xn-2 . y2 + … + nCn yn
General Term = Tr+1 = nCr xn-r . yr
- General Term in (1 + x)n is nCr xr
- In the binomial expansion of (x + y)n , the rth term from end is (n – r + 2)th .
Example 1
Expand (x/3 + 2/y)4
Solution
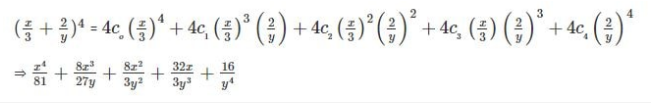
Example 2
Using binominal theorem , (√2 + 1)5 + (√2 − 1)5
Solution
We have
(x + y)5 + (x – y)5 = 2[5C0 x5 + 5C2 x3 y2 + 5C4 xy4]
= 2(x5 + 10 x3 y2 + 5xy4)
Now (√2 + 1)5 + (√2 − 1)5 = 2[(√2)5 + 10(√2)3(1)2 + 5(√2)(1)4]
=58√2
Example 3
Find the number of terms in (1 + 2x +x2)50
Solution
(1 + 2x + x2)50 = [(1 + x)2]50 = (1 + x)100
The number of terms = (100 + 1) = 101
Example 4
Find the fourth term from the end in the expansion of (2x – 1/x2)10
Solution
Required term =T10 – 4 + 2 = T8 = 10C7 (2x)3 (−1/x2)7 = −960x-11
Key takeaways –
- The Binomial Theorem is the method of expanding an expression which has been raised to any finite power
Sources
I.B. N. Gupta : Business Math & Statistics
II. S. P. Singh : Statistics
III. Mukund Lal : Statistics
IV. K. N. Nayar : Statistics
V. C. B. Gupta : Statistics
VI. Shukla & Sahay : Statistical Analysis
VII. C. D. Gupta : Statistical Analysis
VIII. D. N. Elhana : Statistical Analysis