UNIT 2
Set Theory
Set Theory is a branch of mathematics in which we study about sets and their properties. Georg Cantor (1845-1918), a German mathematician, initiated the concept ‘Theory of sets’ or ‘Set Theory’.
Definition
A set is any collection of objects specified in such a way that we can determine whether a given object is or is not in the collection. In other words a set is the collection of objects. These objects are called elements or members of the set.
The following points are noted while writing a set
- Set are usually denoted by capital letters A, B, S, etc.
- The elements of the set are usually denoted by small letters a, b, t, etc
Examples –
A = {a, b,c, d}
C = {maths, science, history, English}
The symbol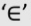 
is used to denote belongs to or is an element of or is a member of a set.
a is an element of set A
a is not an element of set A
Representation of set
- Statement form - In this form, the well-defined description of the elements of the set is given.
Ex - The set of all even number less than 10.
2. Roaster form - In this form, elements are listed within the pair of brackets {} and are separated by commas
Ex - Let N is the set of natural numbers less than 5.
N = { 1 , 2 , 3, 4 }.
3. Set builder form - In Set-builder set is described by a property that its member must satisfy.
- {x : x is even number divisible by 6 and less than 100}
Types of sets
- Empty sets – the sets that contains no members is called empty sets or null sets. The empty set is written as { }
- Equal sets - Two sets are said to be equal if both have same elements. For example A = {1, 3, 9, 7} and B = {3, 1, 7, 9} are equal sets.
- Subsets – sets which are the part of another set is called subsets of the original sets. Ex – if A = {1,2,3,4} and B = {1,2}. Then B is the subset of A
- Power set – if ‘A’ is any set then one set of all are subset of A that it is called a power set. Ex - What is the power set of {0,1,2}?
Solution: All possible subsets
{∅}, {0}, {1}, {2}, {0,1}, {0,2}, {1,2}, {0,1,2}.
Key takeaways –
- Set theory, branch of mathematics that deals with the properties of well-defined collections of objects such as numbers or functions.
Union Intersection and Difference of Sets
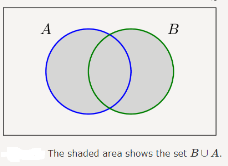
The union of two sets contains all the elements contained in either set (or both sets).
The union is notated A ⋃ B. A∪B={x:x∈A or x∈B}
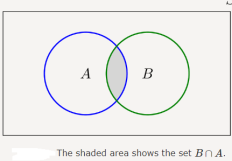
The intersection of two sets contains only the elements that are in both sets.
The intersection is notated A ⋂ B.A∩B={x:x∈A and x∈B}
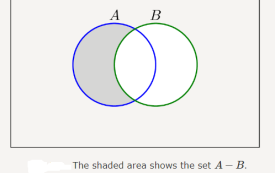
The difference is the set of all thongs that are in A but not in B.
A−B={x:x∈A and x∉B}
Example 1
Consider the sets: A = {red, green, blue} B = {red, yellow, orange}
Find A ⋃ B, A ⋂ B, A-B
Solution
Find A ⋃ B
The union contains all the elements in either set: A ⋃ B = {red, green, blue, yellow, orange}
Note we only list red once
Find A ⋂ B
The intersection contains all the elements in both sets: A ⋂ B = {red}
Find A-B
The difference contains A-B = {green, blue}
Example 2
A={a,b,c,d,e} , B={d,e,f} and C={1,2,3} .
Solution
A∪B={a,b,c,d,e,f}
A∩B={d,e}
A−B={a,b,c}
B−A={f}
(A−B)∪(B−A)={a,b,c,f}
A∪C={a,b,c,d,e,1,2,3}
A∩C={∅}
A−C={a,b,c,d,e}
(A∩C)∪(A−C)={a,b,c,d,e}
(A∩B)×B={(d,d),(d,e),(d,f),(e,d),(e,e),(e,f)}
(A×C)∪(B×C)={(d,1),(d,2),(d,3),(e,1),(e,2),(e,3)}
Example 3
Suppose H = {cat, dog, rabbit, mouse}, F = {dog, cow, duck, pig, rabbit}
W = {duck, rabbit, deer, frog, mouse}
a) Find (H ⋂ F) ⋃ W
b) Find H ⋂ (F ⋃ W)
Solution
a) Find (H ⋂ F) ⋃ W
We start with the intersection: H ⋂ F = {dog, rabbit}
Now we union that result with W: (H ⋂ F) ⋃ W = {dog, duck, rabbit, deer, frog, mouse}
b) Find H ⋂ (F ⋃ W)
We start with the union: F ⋃ W = {dog, cow, rabbit, duck, pig, deer, frog, mouse}
Now we intersect that result with H: H ⋂ (F ⋃ W) = {dog, rabbit, mouse}
Example 4
If the universal set is given by S={1,2,3,4,5,6}, and A={1,2}, B={2,4,5},C={1,5,6} are three sets, find the following sets:
A∪B
A∩B
A
B
Solution
A∪B={1,2,4,5}.
A∩B={2}.
A ={3,4,5,6} (A consists of elements that are in S but not in A).
B ={1,3,6}.
Key takeaways –
2. The union A∪B is the set of all things that are in A or in B (or in both). The intersection A∩B is the set of all things in both A and B. The difference A−B is the set of all things that are in A but not in B.
Elementary Ideas of Determinations and Matrices, Variables and Functions
Matrices
Set of numbers or objects or symbols represented in the form of the rectangular array is called a matrix.
For example
Matrix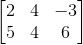 
has 2 rows and 3 columns so its order is said to be 2 × 3.
The determinant of a matrix: a number which is calculated from the matrix. For determinant to exist, matrix A must be a square matrix. The determinant of a matrix is denoted by det A or |A|.
For a 2×2 Matrix
For a 2×2 matrix (2 rows and 2 columns):
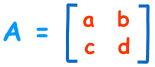
The determinant is:
|A| = ad – bc
"The determinant of A equals a times d minus b times c"
For a 3×3 Matrix
For a 3×3 matrix (3 rows and 3 columns):
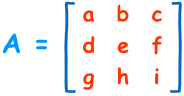
The determinant is:
|A| = a(ei−fh) − b(di −fg) + c(dh −eg)
"The determinant of A equals ... Etc"
Operations on matrices
Addition and subtraction – two matrices may be added if they are in same order
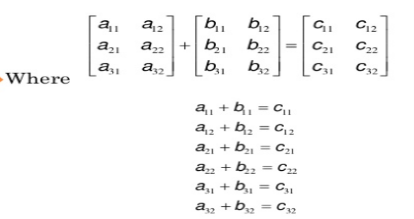
Scalar multiplication – to multiply scalar times a a matrix, simply multiplying each element of the matrix by the scalar quantity
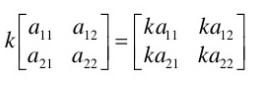
Multiplication matrix - We can only multiply matrices if the number of columns in the first matrix is the same as the number of rows in the second matrix.
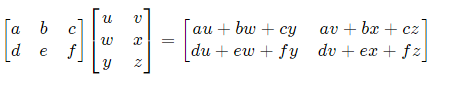
Example 1
Multiply matrix
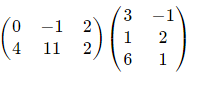
Solution
This is 2×3 times 3×2, which will give us a 2×2 answer
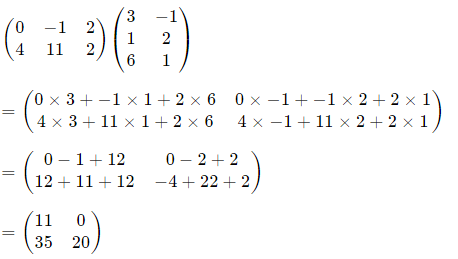
Our answer is a 2×2 matrix.
Example 2
Multiply matrix
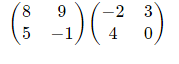
Solution
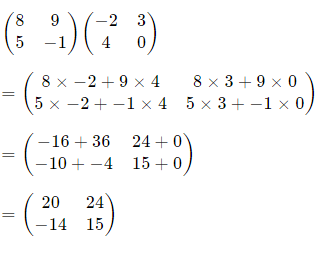
Example 3
If possible, find BA and AB
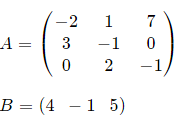
Solution
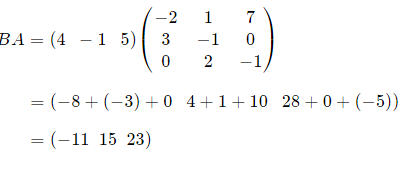
AB is not possible. (3 × 3) × (1 × 3)
Example 3
Calculate the determinants of
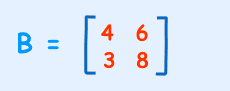
Solution
B = 4*8 – 6*3
= 32 – 18 = 14
Example 4
Calculate the determinants of
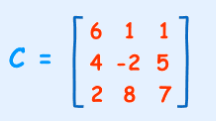
Solution
C = 6×(−2×7 − 5×8) − 1×(4×7 − 5×2) + 1×(4×8 − (−2×2))
= 6×(−54) − 1×(18) + 1×(36)
= −306
Key takeaways – The determinant of a matrix is a special number that can be calculated from a square matrix
Variables and Functions
Definition:
A function is a mathematical relationship in which the values of a single dependent variable are determined by the values of one or more independent variables. Function means the dependent variable is determined by the independent variable(s).
Variables
A variable is an alphabet which is used to represent the unknown number. It represents the value.
For example, x + 5 = 10
Here “x” is a variable.
Types of variables
Dependent Variable - The dependent variable is a variable that depends on the value of some other number or variable. In short, the dependent variable is the output of a function. The value of the dependent variable changes, if there is a change in the value of an independent variable
Example: y = 4 + 2x
Here, y is called a dependent variable. The value of y completely depends on the function 4 + 2x
Independent Variable -The independent variable does not depend on any values. It is called the input of a function. The value of the independent variable is not affected by any values of a function.
Example: x = 2y + 3z
Here, x is called a dependent variable
y and z are the independent variables
Examples
Find the value of the variable y for the equation y = 2x2 when x = 5
Solution:
Given equation: y = 2x2
Here x is called independent variable
Y is called dependent variable
When x = 5, the value of y becomes:
y = 2x2
Now, substituting x = 5 in the given equation, we get
y = 2(5)2
y = 2(25)
y = 50
Therefore, the value of y is 50, when x = 5
Example
Two or more functions can be added, subtracted, multiplied or divided.
g(x) = x - 3 h(x) = x2 + 2
Find g(0) + h(0)
g(0) = 0 - 3 = -3
h(0) = 02 + 2 = 2
g(0) + h(0) = -3 + 2 = -1
Find g(1) h(2)
g(1) = 1 - 3 = -2
h(2) = 22 + 2 = 6
g(1) h(2) = (-2) ( 6) = -12
Example
y = f(x) = 3x + 4
Find f(0), Find f(1), Find f(-1)
Solution
Find f(0). This means find the value of y when x equals 0.
f(0) = 3 times 0 plus 4
f(0) = 3(0) + 4 = 4
Find f(1). This means find the value of y when x equals 1.
f(1) = 3 times 1 plus 4
f(1) = 3(1) + 4 = 7
Find f(-1). This means find the value of y when x equals -1.
f(-1) = 3 times (-1) plus 4
f(1) = 3(-1) + 4 = 1
Key takeaways –
- A function is a mathematical relationship in which the values of a single dependent variable are determined by the values of one or more independent variables.
Sources
I.B. N. Gupta : Business Math & Statistics
II. S. P. Singh : Statistics
III. Mukund Lal : Statistics
IV. K. N. Nayar : Statistics
V. C. B. Gupta : Statistics
VI. Shukla & Sahay : Statistical Analysis
VII. C. D. Gupta : Statistical Analysis
VIII. D. N. Elhana : Statistical Analysis
