UNIT 4
Statistical Tools and Interpretation
A measure of central tendency is a statistical summary that represents the center point of the dataset. It indicates where most values in a distribution fall. It is also called as measure of central location.
The three most common measure of central tendency are Mean, Median, and Mode.
Definition
According to Prof Bowley “Measures of central tendency (averages) are statistical constants which enable us to comprehend in a single effort the significance of the whole.”
Requisites of a good measure of central tendency
- It should be rigidly defined
- It should be simple to understand and easy to calculate
- It should be based upon all values of given data.
- It should be capable of further mathematical treatment.
- It should have sampling stability.
- It should be not be unduly affected by extreme values.

Mean
- The mean is the arithmetic average, also called as arithmetic mean.
- Mean is very simple to calculate and is most commonly used measure of the center of data.
- Means is calculated by adding up all the values and divided by the number of observation.
Computation of sample mean -
If X1, X2, ………………Xn are data values then arithmetic mean is given by
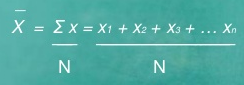
Computation of the mean for ungrouped data
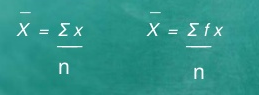
Example 1 – The marks obtained in 10 class test are 25, 10, 15, 30, 35


 The mean = X = 25+10+15+30+35 = 115 =23
The mean = X = 25+10+15+30+35 = 115 =23
5 5
Analysis – the average performance of 5 students is 23. The implication that students who got below 23 did not perform well. The students who got above 23 performed well in exam.
Example 2 – find the mean
Xi | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
Freq (Fi) | 2 | 5 | 12 | 17 | 14 | 6 | 3 |
Xi | Freq (Fi) | XiFi |
9 | 2 | 18 |
10 | 5 | 50 |
11 | 12 | 132 |
12 | 17 | 204 |
13 | 14 | 182 |
14 | 6 | 84 |
15 | 3 | 45 |
| Fi = 59 | XiFi= 715 |
|
|
|
Then, N = ∑ fi = 59, and ∑fi Xi=715
 X = 715/59 = 12.11
X = 715/59 = 12.11
Mean for grouped data
Grouped data are the data that are arranged in a frequency distribution
Frequency distribution is the arrangement of scores according to category of classes including the frequency.
Frequency is the number of observations falling in a category
The formula in solving the mean for grouped data is called midpoint method. The formula is
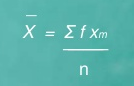
 Where,X = Mean
Where,X = Mean
Xm = midpoint of each class or category
f = frequency in each class or category
∑f Xm = summation of the product of fXm
Example 3 – the following data represent the income distribution of 100 families. Calculate mean income of 100 families?
Income | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
No. Of families | 8 | 12 | 25 | 22 | 16 | 11 | 6 |
Solution
Income | No. Of families | Xm (Mid point) | FXm |
30-40 | 8 | 35 | 280 |
40-50 | 12 | 34 | 408 |
50-60 | 25 | 55 | 1375 |
60-70 | 22 | 65 | 1430 |
70-80 | 16 | 75 | 1200 |
80-90 | 11 | 85 | 935 |
90-100 | 6 | 95 | 570 |
| n = 100 |
| ∑f Xm = 6198 |

X = ∑f Xm/n = 6330/100 = 63.30
Mean = 63.30
Example 4 – calculate the mean number of hours per week spent by each student in texting message.
Time per week | 0 - 5 | 5 - 10 | 10 - 15 | 15 - 20 | 20 - 25 | 25 – 30 |
No. Of students | 8 | 11 | 15 | 12 | 9 | 5 |
Solution
Time per week (X) | No. Of students (F) | Mid point X | XF |
0 - 5 | 8 | 2.5 | 20 |
5 – 10 | 11 | 7.5 | 82.5 |
10 - 15 | 15 | 12.5 | 187.5 |
15 - 20 | 12 | 17.5 | 210 |
20 - 25 | 9 | 22.5 | 202.5 |
25 – 30 | 5 | 27.5 | 137.5 |
| 60 |
| 840 |
Mean = 840/60 = 14
Example 5 –
The following table of grouped data represents the weights (in pounds) of all 100 babies born at a local hospital last year.
Weight (pounds) | Number of Babies |
[3−5) | 8 |
[5−7) | 25 |
[7−9) | 45 |
[9−11) | 18 |
[11−13) | 4 |
Solution
Weight (pounds) | Number of Babies | Mid point X | XF |
[3−5) | 8 | 4 | 32 |
[5−7) | 25 | 6 | 150 |
[7−9) | 45 | 8 | 360 |
[9−11) | 18 | 10 | 180 |
[11−13) | 4 | 12 | 48 |
| 100 |
| 770 |
Mean = 770/100 = 7.7
Importance of mean
- It is rigidly defined
- It is easy to understand and easy to calculate
- It is based upon all values of the given data
- It is capable of future mathematical treatment
- It is not much affected by sampling fluctuation
Demerits of mean
- It cannot be calculated if any observation are missing
- It cannot be calculated for open end classes
- It is effected by extreme values
- It cannot be located graphically
- It may be number which is not present in the data
Key takeaways - The mean is the arithmetic average
Median
- The points or value that divides the data into two equal parts
- Firstly , the data are arranged in ascending or descending order .
- The median is the middle number depending on the data size.
- When the data size is odd, the median is the middle value
- When the data size is even, median is the average of the middle two values
- It is also known as middle score or 50th percentile
 For ungrouped data median is calculated by (n+1)th value
For ungrouped data median is calculated by (n+1)th value
2
Example 1 – find the median score of 7 students in science class
Score = 19, 17, 16, 15, 12, 11, 10
Median = (7+1)/2 = 4th value
Median = 15
Find the median score of 8 students in science class
Score = 19, 17, 16, 15, 12, 11, 10, 9
Median = (8+1)/2 = 4.5th value
Median = (15+12)/2 = 13.5
Example 2 – find the median of the table given below
Marks obtained | No. Of students |
20 | 6 |
25 | 20 |
28 | 24 |
29 | 28 |
33 | 15 |
38 | 4 |
42 | 2 |
43 | 1 |
Solution
Marks obtained | No. Of students | Cf |
20 | 6 | 6 |
25 | 20 | 26 (20+6) |
28 | 24 | 50 (26+24) |
29 | 28 | 78 |
33 | 15 | 93 |
38 | 4 | 97 |
42 | 2 | 99 |
43 | 1 | 100 |
Median = (n+1)/2 = 100+1/2 = 50.5
Median = (28+29)/2 = 28.5
Median of grouped data
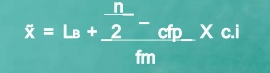
Formula
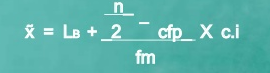
 MC = median class is a category containing the n/2
MC = median class is a category containing the n/2
Lb = lower boundary of the median class
Cfp = cumulative frequency before the median class if the scores are arranged from lowest to highest value
Fm = frequency of the median class
c.i = size of the class interval
Ex- calculate the median
Example 3-
Calculate the median
Marks | No. Of students |
0-4 | 2 |
5-9 | 8 |
10-14 | 14 |
15-19 | 17 |
20-24 | 9 |
Solution
Marks | No. Of students | CF |
0-4 | 2 | 2 |
5-9 | 8 | 10 |
10-14 | 14 | 24 |
15-19 | 17 | 41 |
20-24 | 9 | 50 |
| 50 |
|
n = 50
 n = 50/2= 25
n = 50/2= 25
2
The category containing n/2 is 15 -19
Lb = 15
Cfp = 24
f = 17
Ci = 4

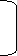
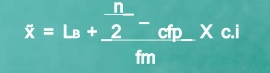
 Median = 15 + 25-24 *4 = 15.23
Median = 15 + 25-24 *4 = 15.23
17
Example 4 - Given the below frequency table calculate median
X | 60 – 70 | 70 – 80 | 80- 90 | 90-100 |
F | 4 | 5 | 6 | 7 |
Solution
X | F | CF |
60 - 70 | 4 | 4 |
70 - 80 | 5 | 9 |
80 - 90 | 6 | 15 |
90 - 100 | 7 | 22 |
n = 22
 n = 22/2= 11
n = 22/2= 11
2
The category containing n+1/2 is 80 - 90
Lb = 80
Cfp = 9
f = 6
Ci = 10

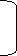
 Median = 80 + 11-9 *10 = 83.33
Median = 80 + 11-9 *10 = 83.33
6
Example 5– calculate the median of grouped data
Class interval | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 |
Frequency | 4 | 12 | 13 | 19 | 7 | 5 |
Solution
CI | F | CF |
1-3 | 4 | 4 |
3-5 | 12 | 16 |
5-7 | 13 | 29 |
7-9 | 19 | 48 |
9-11 | 7 | 55 |
11-13 | 5 | 60 |
n = 60
 n = 60/2= 30
n = 60/2= 30
2
The category containing n+1/2 is 7-9
Lb = 7
Cfp = 29
f = 19
Ci = 2
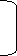

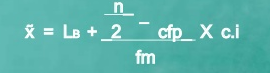
 Median = 7 + 30-29 *2 = 7.105
Median = 7 + 30-29 *2 = 7.105
19
Example 5 -
Importance of median
- It is rigidly defined
- It is easy to understand and easy to calculate
- It is not effected by extreme values
- It is not much affected by sampling fluctuation
- It can be located graphically
Demerits of median
- It is not based upon all values of the given data
- It is difficult to calculate increasing order data size
- It is not capable of further mathematical treatment.
Key takeaways - The points or value that divides the data into two equal parts
Mode
- The mode is denoted Mo, is the value which occurs most frequently in a set of values.
- Croxton and Cowden defined it as “the mode of a distribution is the value at the point armed with the item tends to most heavily concentrated. It may be regarded as the most typical of a series of value”
Mode for ungrouped data
Example 1- Find the mode of scores of section A
Scores = 25, 24, 24, 20, 17, 18, 10, 18, 9, 7
Solution – Mode is 24, 18 as both have occurred twice.
Mode for grouped data
 Mode = L1 + (L2 – L1) d1
Mode = L1 + (L2 – L1) d1
d1 +d2
L1= lower limit of the modal class,
L2= upper limit of the modal class‟
d1 =fm-f0 and d2=fm-f1
Where fm= frequency of the modal class,
f0 = frequency of the class preceding to the modal class,
f1= frequency of the class succeeding to the modal class.
Example 2 – find the mode
Seconds | Frequency |
51 - 55 | 2 |
56 - 60 | 7 |
61 - 65 | 8 |
66 - 70 | 4 |
The group with the highest frequency is the modal group: - 61-65
D1 = 8-7 = 1
D2 = 8-4 = 4
 Mode = L1 + (L2 – L1) d1
Mode = L1 + (L2 – L1) d1
d1 +d2
 mode = 61 + (65-61) 1 = 61+4 (1/5) = 61.8
mode = 61 + (65-61) 1 = 61+4 (1/5) = 61.8
1+4
Mode = 61.8
Example 3 - In a class of 30 students marks obtained by students in science out of 50 is tabulated below. Calculate the mode of the given data.
Marks obtained | No. Of students |
10 -20 | 5 |
20 – 30 | 12 |
30 – 40 | 8 |
40 – 50 | 5 |
Solution
The group with the highest frequency is the modal group: - 20 -30
D1 = 12 - 5 = 7
D2 = 12 - 8 = 4
 Mode = L1 + (L2 – L1) d1
Mode = L1 + (L2 – L1) d1
d1 +d2
 mode = 20 + (30-20) 7 = 20+10 (7/11) = 26.36
mode = 20 + (30-20) 7 = 20+10 (7/11) = 26.36
7+4
Mode = 61.8
Example 4- Based on the group data below, find the mode
Time to travel to work | Frequency |
1 – 10 | 8 |
11 -20 | 14 |
21 – 30 | 12 |
31 – 40 | 9 |
41 – 50 | 7 |
Solution
The group with the highest frequency is the modal group: - 11 - 20
D1 = 14 - 8 = 6
D2 = 14 - 12 = 2
 Mode = L1 + (L2 – L1) d1
Mode = L1 + (L2 – L1) d1
d1 +d2
 mode = 11 + (20-11) 6 = 11+9 (6/8) = 17.75
mode = 11 + (20-11) 6 = 11+9 (6/8) = 17.75
6+2
Example 5 –
Compute the mode from the following frequency distribution
CI | F |
70-71 | 2 |
68-69 | 2 |
66-67 | 3 |
64-65 | 4 |
62-63 | 6 |
60-61 | 7 |
58-59 | 5 |
Solution
The group with the highest frequency is the modal group: - 60 - 61
D1 = 7 - 6 = 1
D2 = 7 - 5 = 2
 Mode = L1 + (L2 – L1) d1
Mode = L1 + (L2 – L1) d1
d1 +d2
 mode = 60 + (61-60) 1 = 60+1 (1/3) 60.85
mode = 60 + (61-60) 1 = 60+1 (1/3) 60.85
1+2
Importance of mode
- It is easy to understand & easy to calculate
- It is not affected by extreme values or sampling fluctuations.
- Even if extreme values are not known mode can be calculated.
- It can be located just by inspection in many cases.
- It is always present within the data.
Demerits of mode
- It is not rigidly defined.
- It is not based upon all values of the given data.
- It is not capable of further mathematical treatment.
Key takeaways - The mode is denoted Mo, is the value which occurs most frequently in a set of values.
Quartiles
There are three quartiles, i.e. Q1, Q2 and Q3 which divide the total data into four equal parts when it has been orderly arranged. Q1, Q2 and Q3 are termed as first quartile, second quartile and third quartile or lower quartile, middle quartile and upper quartile, respectively. The first quartile, Q1, separates the first one-fourth of the data from the upper three fourths and is equal to the 25th percentile. The second quartile, Q2, divides the data into two equal parts (like median) and is equal to the 50th percentile. The third quartile, Q3, separates the first three-quarters of the data from the last quarter and is equal to 75th percentile.
Calculation of Quartiles:
The calculation of quartiles is done exactly in the same manner as it is in case of the calculation of median.
The different quartiles can be found using the formula given below:
Qi = l1 + 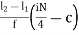 i= 1,2,3
i= 1,2,3
Where,
L1 = lower limit of ith quartile class
L2 = upper limit of ithquartile class
c = cumulative frequency of the class preceding the ithquartile class
f = frequency of ith quartile class.
Deciles
Deciles are the partition values which divide the arranged data into ten equal parts. There are nine deciles i.e. D1, D2, D3……. D9 and 5th decile is same as median or Q2, because it divides the data in two equal parts.
Calculation of Deciles:
The calculation of deciles is done exactly in the same manner as it is in case of calculation of median.
The different deciles can be found using the formula given below:
Di = l1 + 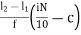 i= 1,2,3….9
i= 1,2,3….9
Where,
l1 = lower limit of ith quartile class
l2 = upper limit of ithquartile class
c = cumulative frequency of the class preceding the ithquartile class
f = frequency of ith quartile class.
Percentile
Percentiles are the values which divide the arranged data into hundred equal parts. There are 99 percentiles i.e. P1, P2, P3, ……. P99.
The 50th percentile divides the series into two equal parts and P50 = D5 = Median.
Similarly, the value of Q1 = P25 and value of Q3 = P75
Calculation of Percentiles:
The different percentiles can be found using the formula given below:
pi = l1 + 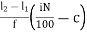 i= 1,2,3…………….99
i= 1,2,3…………….99
Where,
l1 = lower limit of ith quartile class
l2 = upper limit of ithquartile class
c = cumulative frequency of the class preceding the ithquartile class
f = frequency of ith quartile class.
Example 1
Calculate Q1, Q2 and Q3 from the following data given below:
Day | Frequency |
1 | 20 |
2 | 35 |
3 | 25 |
4 | 12 |
5 | 10 |
6 | 23 |
7 | 18 |
8 | 14 |
9 | 30 |
10 | 40 |
ANS
Arrange the frequency data in ascending order
Day | Frequency |
1 | 10 |
2 | 12 |
3 | 14 |
4 | 18 |
5 | 20 |
6 | 23 |
7 | 25 |
8 | 30 |
9 | 35 |
10 | 40 |
First quartile (Q1)
Qi= [i * (n + 1) /4] th observation
Q1= [1 * (10 + 1) /4] th observation
Q1 = 2.75 th observation
Thus, 2.75 th observation lies between the 2nd and 3rd value in the ordered group, between frequency 12 and 14
First quartile (Q1) is calculated as
Q1 = 2nd observation +0.75 * (3rd observation - 2nd observation)
Q1 = 12 + 0.75 * (14 – 12) = 13.50
Third quartile (Q3)
Qi= [i * (n + 1) /4] th observation
Q3= [3 * (10 + 1) /4] th observation
Q3 = 8.25 th observation
So, 8.25 th observation lies between the 8th and 9th value in the ordered group, between frequency 30 and 35
Third quartile (Q3) is calculated as
Q3 = 8th observation +0.25 * (9th observation – 8th observation)
Q3 = 30 + 0.25 * (35 – 30) = 31.25
Example 2
Calculate Q1, D7 and P20 from the following data:
3, 13, 11, 11, 5, 4, 2
ANS
Arranging observations in the ascending order we get
2, 3, 4, 5, 11, 11, 13
Here, n = 7
Q1 = (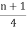 )th value of the observation
)th value of the observation
= ( )th Value of the observation
)th Value of the observation
= 2nd Value of the observation
= 3
D3 = (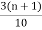 )th value of the observation
)th value of the observation
= (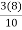 )th value of the observation
)th value of the observation
= (2.4)th Value of the observation
= 2nd observation + 0.4 (3rd – 2nd)
= 3 + 0.4(4 – 3)
= 3 + 0.4
= 3.4
P20 = (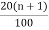 )th value of the observation
)th value of the observation
= (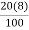 )th value of the observation
)th value of the observation
= (1.6)th value of the observation
= 1st observation + 0.6 (2nd – 1st )
= 2 + 0.6(3 – 2)
= 2 + 0.6
= 2.6
Example 3
Calculate P20 from the following data:
Class | 2 - 4 | 4 - 6 | 6 - 8 | 8 - 10 |
Frequency | 3 | 4 | 2 | 1 |
ANS
In the case of Frequency Distribution, Percentiles can be calculated by using the formula:
pi = l1 + 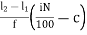
Class interval | F | CF |
2 – 4 | 3 | 3 |
4 – 6 | 4 | 7 |
6 – 8 | 2 | 9 |
8 – 10 | 1 | 10 |
Total | n = 10 |
|
Here n = 10
Class with 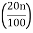 th value of the observation in CF column
th value of the observation in CF column
= 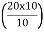 th value of the observation in CF column
th value of the observation in CF column
= 2th value of the observation in CF column and it lies in the class 2 - 4
Therefore, P20 class is 2 – 4
The lower boundary point of 2 – 4 is 2.
Therefore, L = 2
P20 = L + 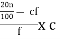
= 2 + 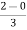 x 2
x 2
= 2 + 1.3333
= 3.3333
Example 4
Calculate D7 from the following data:
Class | 2 - 4 | 4 - 6 | 6 - 8 | 8 - 10 |
Frequency | 3 | 4 | 2 | 1 |
ANS
In the case of Frequency Distribution, Deciles can be calculated by using the formula:
Di = l1 + 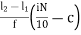
Class interval | F | CF |
2 – 4 | 3 | 3 |
4 – 6 | 4 | 7 |
6 – 8 | 2 | 9 |
8 – 10 | 1 | 10 |
Total | n = 10 |
|
Here n = 10
Class with 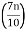 th value of the observation in CF column
th value of the observation in CF column
= 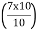 th value of the observation in CF column
th value of the observation in CF column
= 7th value of the observation in CF column and it lies in the class 6 – 8
Therefore, D7 class is 6 – 8
The lower boundary point of 6 – 8 is 6.
Therefore, L = 6
D7 = L + 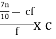
= 6 + 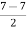 x 2
x 2
= 6 + 0
= 6
Example 5
Calculate Q1, Q2 and Q3 from the following data given below:
Age in years | 40 -44 | 45 – 49 | 50 – 54 | 55 - 59 | 60 – 64 | 65 - 69 |
Employees | 5 | 8 | 11 | 10 | 9 | 7 |
ANS
In the case of Frequency Distribution, Quartiles can be calculated by using the formula:
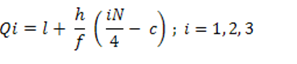
Class interval | F | Class boundaries | CF |
40 -44 | 5 | 39.5 – 44.5 | 5 |
45 – 49 | 8 | 44.5 – 49.5 | 13 |
50 – 54 | 11 | 49.5 – 54.5 | 24 |
55 – 59 | 10 | 54.5 – 59.5 | 34 |
60 – 64 | 9 | 59.5 – 64.5 | 43 |
65 – 69 | 7 | 64.5 – 69.5 | 50 |
Total | 50 |
|
|
First quartile (Q1)
Qi= [i * (n ) /4] th observation
Q1 = [1*(50)/4]th observation
Q1 = 12.50th observation
So, 12.50th value is in the interval 44.5 – 49.5
Group of Q1 = 44.5 – 49.5
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q1 = (44.5 + ( 5/ 8)* (1* (50/4) – 5)
Q1 = 49.19
Third quartile (Q3)
Qi= [i * (n) /4] th observation
Q3= [3 * (50) /4] th observation
Q3 = 37.5th observation
So, 37.5th value is in the interval 59.5 – 64.5
Group of Q3 = 59.5 – 64.5
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q3 = (59.5 + ( 5/ 9)* (3* (50/4) – 34)
Q3 = 61.44
Key takeaways –
- A decile is used to categorize large data sets from highest to lowest values, or vice versa.While quartiles are three data points that divide an observation into four equal groups or quarters
Central tendency do not reveal the variability present in the data. Dispersion measures the scatteredness of the data series around its average. It tells the variation of the data from one another and gives a clear idea about the distribution of the data.
Definition
In statistics, dispersion is extent to which a distribution is stretched or squeezed.
Characteristics of measures of dispersion
- It should be rigidly defined
- It should be easy to understand and calculate
- Must be based on all observation of the data
- Must be less affected by sampling fluctuation
Types of measures of dispersion
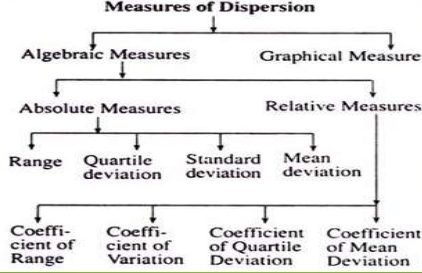
Algebraic measures – It includes the mathematical way to calculate the measures of dispersion.
Graphical measures – The way to calculate the measures of dispersion by graphs and figures
Absolute measures of dispersion – It gives an idea about the amount of dispersion in a set of observations. It measures the dispersion in the same units as the units of original data. Absolute measures cannot be used for comparison of two or more data set variations.
Relative measures of dispersion – the relative measures of distribution are used for comparing the distribution of two or more data sets.
Coefficients of dispersion are used to compare two series with different measurement of unit.
Types of absolute measures of dispersion
- Range – Range defines the difference between the maximum value and the minimum value given in a data set. More the range , group is more variable. The smaller the range the more homogenous is the group.
R = H – L
Example 1 – 5, 10, 15, 20, 7, 9, 17, 13, 12, 16, 8, 6
Range = H-L
=20 – 5 = 15
Coefficient of range –

Coefficient of range = (15/(20+5))*100 = 60
Example 2 – what is the range for the following set of numbers?
15,21,57,43,11,39,56,83,77,11,64,91,18,37
Solution
Range = H-L
= 91 – 11 = 80
Therefore the range is 80
Example 3 – the frequency table shows the number of goals the lakers scored in their last twenty matches. What was the range
No. Of goals | Frequency |
0 | 2 |
1 | 3 |
2 | 3 |
3 | 6 |
4 | 3 |
5 | 1 |
6 | 1 |
7 | 1 |
Solution
The range is the difference between the lowest and highest values.
The highest value was 7 (They scored 7 goals on 1 occasion)
The lowest value was 0 (They scored 0 goals on 2 occasions)
Therefore the range = 7 - 0 = 7
Example 4 – the following table shows the sales of DVD players made by a retail store each month last year
Month | No. Of sales |
January | 25 |
Feb | 43 |
March | 39 |
April | 28 |
May | 29 |
June | 35 |
July | 32 |
August | 46 |
September | 28 |
October | 43 |
November | 51 |
December | 63 |
Solution
The range is the difference between the lowest and highest values.
The lowest number of sales = 25 in January
The highest number of sales = 63 in December
So the range = 63 - 25 = 38
Example 5 – what is the range for the following set of numbers?
57, -5, 11, 39, 56, 82, -2, 11, 64, 18, 37, 15, 68
Solution
The range is the difference between the lowest and highest values.
The highest value is 82.
The lowest value is -5.
Therefore the range = 82 - (-5) = 82+5 = 87
Merits
- Simple and easy to understand
- It gives a quick answer
Demerits
- It is not based on all observation
- Affected by sampling fluctuations
- It cannot be calculated in open ended distributions
2. Interquartile range - the interquartile range measures the range of the middle 50% of the values only. It is calculated as the difference between the upper and lower quartile.
Interquartile range = upper quartile – lower quartile
= Q3 – Q1
Examples 1– find the interquartile range for 1, 2, 18, 6, 7, 9, 27, 15, 5, 19, 12.
Solution
Arrange the numbers in ascending order
1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27
Find the median
Median = 9
(1, 2, 5, 6, 7), 9, (12, 15, 18, 19, 27)
Q1 as median in the lower half and Q3 as median in the upper half
Q1 = median in (1, 2, 5, 6, 7)
Q1 = 5
Q3 = median in (12, 15, 18, 19, 27)
Q3 = 18
Interquartile range = 18 – 5 = 13
Example 2 – find the interquartile for the following data set: 3, 5, 7, 8, 9, 11, 15, 16, 20, 21.
Solution
Arrange the numbers in ascending order
3, 5, 7, 8, 9, 11, 15, 16, 20, 21
Make a mark in the center of the data:
(3, 5, 7, 8, 9,) | (11, 15, 16, 20, 21)
Find the median
Q1 = 7
Q3 = 16
Interquartile range = 16 – 7 = 9
Example 3 - find the interquartile for the following data set: 1, 3, 4, 5, 5, 6, 7, 11
Make a mark in the center of the data:
(1, 3, 4, 5,) (5, 6, 7, 11)
Find the median
Q1 = (3+4)/2 = 3.5
Q3 = (6+7)/2 = 6.5
Interquartile range = 6.5 – 3.5 = 3
Example 4 -
Find the interquartile range for odd sample size
63,64,64,70,72,76,77,81,81
Solution
Make a mark in the center of the data:
(63,64,64,70,)72,(76,77,81,81)
Find the median
Q1 = (64+64)/2 = 64
Q3 = (77+81)/2 = 79
Interquartile range = 79 – 64 = 15
3. Quartile deviation
Quartile deviation is the product of half of the difference between the upper and the lower quartiles.
QD = (Q3 - Q1) / 2
Coefficient of Quartile Deviation = (Q3 – Q1) / (Q3 + Q1)
Quartile deviation for ungrouped data
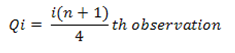
Examples 1
Day | Frequency |
1 | 20 |
2 | 35 |
3 | 25 |
4 | 12 |
5 | 10 |
6 | 23 |
7 | 18 |
8 | 14 |
9 | 30 |
10 | 40 |
Solution
Arrange the frequency data in ascending order
Day | Frequency |
1 | 10 |
2 | 12 |
3 | 14 |
4 | 18 |
5 | 20 |
6 | 23 |
7 | 25 |
8 | 30 |
9 | 35 |
10 | 40 |
First quartile (Q1)
Qi= [i * (n + 1) /4] th observation
Q1= [1 * (10 + 1) /4] th observation
Q1 = 2.75 th observation
Thus, 2.75 th observation lies between the 2nd and 3rd value in the ordered group, between frequency 12 and 14
First quartile (Q1) is calculated as
Q1 = 2nd observation +0.75 * (3rd observation - 2nd observation)
Q1 = 12 + 0.75 * (14 – 12) = 13.50
Third quartile (Q3)
Qi= [i * (n + 1) /4] th observation
Q3= [3 * (10 + 1) /4] th observation
Q3 = 8.25 th observation
So, 8.25 th observation lies between the 8th and 9th value in the ordered group, between frequency 30 and 35
Third quartile (Q3) is calculated as
Q3 = 8th observation +0.25 * (9th observation – 8th observation)
Q3 = 30 + 0.25 * (35 – 30) = 31.25
Now using the quartiles values Q1 and Q3, we will calculate the quartile deviation.
QD = (Q3 - Q1) / 2
QD = (31.25 – 13.50) / 2 = 8.875
Coefficient of Quartile Deviation = (Q3 – Q1) / (Q3 + Q1)
= (31.25 – 13.50) /(31.25 + 13.50) = 0.397
Example 2 – calculate quartile deviation from the following test scores
Sl. N o | Test scores |
1 | 17 |
2 | 17 |
3 | 26 |
4 | 27 |
5 | 30 |
6 | 30 |
7 | 31 |
8 | 37 |
Solution
First quartile (Q1)
Qi= [i * (n + 1) /4] th observation
Q1= [1 * (8 + 1) /4] th observation
Q1 = 2.25 th observation
Thus, 2.25 th observation lies between the 2nd and 3rd value in the ordered group, between frequency 17 and 26
First quartile (Q1) is calculated as
Q1 = 2nd observation +0.75 * (3rd observation - 2nd observation)
Q1 = 17 + 0.75 * (26 – 17) = 23.75
Third quartile (Q3)
Qi= [i * (n + 1) /4] th observation
Q3= [3 * (8 + 1) /4] th observation
Q3 = 6.75 th observation
So, 6.75 th observation lies between the 6th and 7th value in the ordered group, between frequency 30 and 31
Third quartile (Q3) is calculated as
Q3 = 6th observation +0.25 * (7th observation – 6th observation)
Q3 = 30 + 0.25 * (31 – 30) = 30.25
Now using the quartiles values Q1 and Q3, we will calculate the quartile deviation.
QD = (Q3 - Q1) / 2
QD = (30.25 – 23.75) / 2 = 3.25
Quartile deviation for grouped data
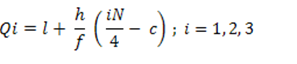
Where,
l = lower boundary of quartile group
h = width of quartile group
f = frequency of quartile group
N = total number of observation
C= cumulative frequency preceding quartile group
Example 3
Age in years | 40 -44 | 45 – 49 | 50 – 54 | 55 - 59 | 60 – 64 | 65 - 69 |
Employees | 5 | 8 | 11 | 10 | 9 | 7 |
Solutions
In the case of Frequency Distribution, Quartiles can be calculated by using the formula:
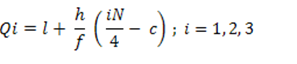
Class interval | F | Class boundaries | CF |
40 -44 | 5 | 39.5 – 44.5 | 5 |
45 – 49 | 8 | 44.5 – 49.5 | 13 |
50 – 54 | 11 | 49.5 – 54.5 | 24 |
55 – 59 | 10 | 54.5 – 59.5 | 34 |
60 – 64 | 9 | 59.5 – 64.5 | 43 |
65 – 69 | 7 | 64.5 – 69.5 | 50 |
Total | 50 |
|
|
First quartile (Q1)
Qi= [i * (n ) /4] th observation
Q1 = [1*(50)/4]th observation
Q1 = 12.50th observation
So, 12.50th value is in the interval 44.5 – 49.5
Group of Q1 = 44.5 – 49.5
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q1 = (44.5 + ( 5/ 8)* (1* (50/4) – 5)
Q1 = 49.19
Third quartile (Q3)
Qi= [i * (n) /4] th observation
Q3= [3 * (50) /4] th observation
Q3 = 37.5th observation
So, 37.5th value is in the interval 59.5 – 64.5
Group of Q3 = 59.5 – 64.5
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q3 = (59.5 + ( 5/ 9)* (3* (50/4) – 34)
Q3 = 61.44
QD = (Q3 - Q1) / 2
QD = (61.44 – 49.19) / 2 = 6.13
Coefficient of Quartile Deviation = (Q3 – Q1) / (Q3 + Q1)
= (61.44 – 49.19) /(61.44 + 49.19) = 0.11
Example 4 – computation of quartile deviation for grouped test scores
Class | Frequency |
9.3-9.7 | 22 |
9.8-10.2 | 55 |
10.3-10.7 | 12 |
10.8-11.2 | 17 |
11.3-11.7 | 14 |
11.8-12.2 | 66 |
12.3-12.7 | 33 |
12.8-13.2 | 11 |
Solution
Class | Frequency | Class boundaries | CF |
9.3-9.7 | 2 | 9.25-9.75 | 2 |
9.8-10.2 | 5 | 9.75-10.25 | 2 + 5 = 7 |
10.3-10.7 | 12 | 10.25-10.75 | 7 + 12 = 19 |
10.8-11.2 | 17 | 10.75-11.25 | 19 + 17 = 36 |
11.3-11.7 | 14 | 11.25-11.75 | 36 + 14 = 50 |
11.8-12.2 | 6 | 11.75-12.25 | 50 + 6 = 56 |
12.3-12.7 | 3 | 12.25-12.75 | 56 + 3 = 59 |
12.8-13.2 | 1 | 12.75-13.25 | 59 + 1 = 60 |
First quartile (Q1)
Qi= [i * (n ) /4] th observation
Q1 = [1*(60)/4]th observation
Q1 = 15th observation
So, 15th value is in the interval 10.25-10.75
Group of Q1 = 10.25-10.75
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q1 = (10.25 + ( 0.5/ 12)* (1* (60/4) – 7)
Q1 = 10.58
Third quartile (Q3)
Qi= [i * (n) /4] th observation
Q3= [3 * (60) /4] th observation
Q3 = 45th observation
So, 45th value is in the interval 11.25-11.75
Group of Q3 = 11.25-11.75
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q3 = (11.25 + ( 0.5/ 14)* (3* (60/4) – 36)
Q3 = 11.57
QD = (Q3 - Q1) / 2
QD = (11.57 – 10.58) / 2 = 0.495
Example 5 – calculate quartile deviation from the following data
CI | F |
10 – 15 | 6 |
15 – 20 | 10 |
20 – 25 | 15 |
25 – 30 | 22 |
30 – 40 | 12 |
40 – 50 | 9 |
50 – 60 | 4 |
60 – 70 | 2 |
Solution
CI | F | Cf |
10 – 15 | 6 | 6 |
15 – 20 | 10 | 16 |
20 – 25 | 15 | 31 |
25 – 30 | 22 | 53 |
30 – 35 | 12 | 65 |
35 – 40 | 9 | 74 |
45 – 50 | 4 | 78 |
55 – 60 | 2 | 80 |
First quartile (Q1)
Qi= [i * (n ) /4] th observation
Q1 = [1*(80)/4]th observation
Q1 = 20th observation
So, 20th value is in the interval 20 - 25
Group of Q1 = 20 - 25
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q1 = (20 + ( 5/ 15)* (1* (80/4) – 16)
Q1 = 21.33
Third quartile (Q3)
Qi= [i * (n) /4] th observation
Q3= [3 * (80) /4] th observation
Q3 = 60th observation
So, 60th value is in the interval 30 - 35
Group of Q3 = 30 - 35
Qi = (I + (h / f) * ( i * (N/4) – c) ; i = 1,2,3
Q3 = (30 + ( 5/ 12)* (3* (80/4) – 53)
Q3 = 32.91
QD = (Q3 - Q1) / 2
QD = (32.91 – 21.33) / 2 = 5.79
Merits
- It provide better result than range mode
- It is not effected by extreme values
Demerits
- It is completely dependent on central item
- All items are not taken onto consideration
4. Mean deviation – The average of the absolute values of deviation from the mean, median or mode is called mean deviation. This method removes shortcoming of range and QD.
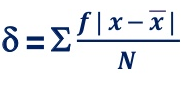
OR
 =
= 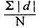
Where, ∑ is total of;
 X is the score, X is the mean, and N is the number of scores
X is the score, X is the mean, and N is the number of scores
D = Deviation of individual scores from mean
Example 1 –
Computation of mean deviation in ungrouped data
X = 55, 45, 39, 41, 40, 48, 42, 53, 41, 56
Solution
X |
| Absolute deviation (signed ignored) |
55 | 55 - 46 = 9 | 9 |
45 | 45 – 46 = -1 | 1 |
39 | -7 | 7 |
41 | -5 | 5 |
40 | -6 | 6 |
48 | 2 | 2 |
42 | -4 | 4 |
53 | 7 | 7 |
41 | -5 | 5 |
56 | 10 | 10 |
∑X = 460 |
|
|
Mean = 460/10 = 46
MD = 56/10 = 5.6
Example 2- Peterdid a surveyod the number of pets owned by his classmates, with the following result. What is the mean deviation of the number of pets?
No. Of pets | Frequency |
0 | 4 |
1 | 12 |
2 | 8 |
3 | 2 |
4 | 1 |
5 | 2 |
6 | 1 |
Solution
X | F | Fx |
|
|
0 | 4 | 0 | 1.8 | 7.2 |
1 | 12 | 12 | 0.8 | 9.6 |
2 | 8 | 16 | 0.2 | 1.6 |
3 | 2 | 6 | 1.2 | 2.4 |
4 | 1 | 4 | 2.2 | 2.2 |
5 | 2 | 10 | 3.2 | 6.4 |
6 | 1 | 6 | 3.2 | 4.2 |
| 30 | 54 | 4.2 | 33.6 |
Mean = 54/30 = 1.8
MD = 33.6/30 = 1.12
Computation of Mean deviation in grouped data
Example 3 -
Class interval | 15 – 19 | 20 – 24 | 25 – 29 | 30 – 34 | 35 – 39 | 40 – 44 | 45 - 49 |
Frequency | 1 | 4 | 6 | 9 | 5 | 3 | 2 |
Class Interval | F | X | FX | D | FD |
15 – 19 | 1 | 17 | 17 | 15 | 15 |
20 – 24 | 4 | 22 | 88 | 10 | 40 |
25 – 29 | 6 | 27 | 162 | 5 | 30 |
30 - 34 | 9 | 32 | 288 | 0 | 0 |
35 - 39 | 5 | 37 | 185 | 5 | 25 |
40 - 44 | 3 | 42 | 126 | 10 | 30 |
45 - 49 | 2 | 47 | 94 | 15 | 30 |
| N = 30 |
| ∑fx = 960 |
|  |
Mean =960/30 = 32
MD = 170 / 30 = 5.667
Coefficient of mean deviation
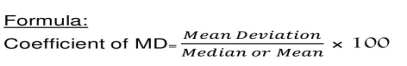
Coefficient of mean deviation = (5.67/32)*100 = 17.71
Example 4 – calculate mean deviation from the median
Class | 5 -15 | 15 – 25 | 25 - 35 | 35 - 45 | 45 – 55 |
Frequency | 5 | 9 | 7 | 3 | 8 |
Solution
x | f | Cf | Mid point x | x –median | F(x-m) |
5 -15 | 5 | 5 | 10 | 17.42 | 87.1 |
15 -25 | 9 | 14 | 20 | 7.42 | 66.78 |
25 -35 | 7 | 21 | 30 | 2.58 | 18.06 |
35 -45 | 3 | 24 | 40 | 12.58 | 37.74 |
45- 55 | 8 | 32 | 50 | 22.58 | 180.64 |
| 32 |
|
|
| 390.32 |
Since n/2 = 32/2 = 16, therefore the class is 25 – 35 is the median.
Median = 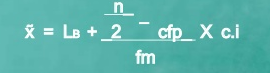
 Median = 25+16-14 *10 = 27.42
Median = 25+16-14 *10 = 27.42
7
MD from median is 390.32/32 = 12.91
Example 5 – calculate the mean deviation from continuous frequency distribution
Age group | 15 - 25 | 25 – 35 | 35 - 45 | 45 - 55 |
No. Of people | 25 | 54 | 34 | 20 |
Solution
Age group (X) | Number of people (f) | Midpoint x | Fx |
|
|
15 – 25 | 25 | 20 | 500 | 13.684 | 324.1 |
25 – 35 | 54 | 30 | 1620 | 3.684 | 198.936 |
35 – 45 | 34 | 40 | 1360 | 6.316 | 214.744 |
45 - 55 | 20 | 50 | 1000 | 16.316 | 352.32 |
| 133 |
|
|
| 1090.1 |
Mean = 4480/133 = 33.684
MD = 1090.1/133 = 8.196
Merits
- It is easy to calculate
- It helps in making comparison
- It is not affected by extreme items
Demerits
- It ignores algebraic sign. And are not used for mathematical treatment
- It is not reliable
5. Standard deviation – standard deviation is calculated as square root of average of squared deviations taken from actual mean. It is also called root mean square deviation. This measure suffers from less drawbacks and provides accurate results. It removes the drawbacks of ignoring algebraic sign. We square the deviation to make them positive.
Two ways of computing SD
- Direct method
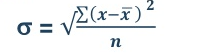
2. Shortcut method
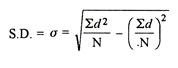
d = Deviation of the score from an assumed mean, say AM; i.e. d = (X – AM). AM is assumed mean
d2 = the square of the deviation.
∑d = the sum of the deviations.
∑d2 = the sum of the squared deviations.
N = No. Of the scores
Standard deviation in ungrouped data
- Direct method
Example 1–
X = 12, 15, 10, 8, 11, 13, 18, 10, 14, 9
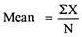
Mean = 120/10 = 12
Scores | D | 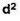 |
12 | 12-12 = 0 | 0 |
15 | 15-12 = 3 | 9 |
10 | 10 -12 = -2 | 4 |
8 | -4 | 16 |
11 | -1 | 1 |
13 | 1 | 1 |
18 | 6 | 36 |
10 | -2 | 4 |
14 | 2 | 4 |
9 | -3 | 9 |
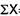 | 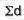 | 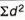 |
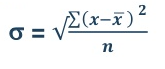
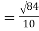 = 2.9
= 2.9
2. Shortcut method
Assumed mean (AM) = 11
Scores | D = (X- AM) | 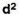 |
12 | 12-11 = 1 | 1 |
15 | 15-11 = 4 | 16 |
10 | 10 -11 = -1 | 1 |
8 | -3 | 9 |
11 | 0 | 0 |
13 | 2 | 4 |
18 | 7 | 49 |
10 | --1 | 1 |
14 | 3 | 9 |
9 | -2 | 4 |
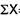 | 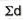 | 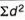 |
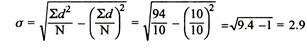
SD from short cut method = 2.9
Example 2 –Ram did a survey of the number of pets owned by his classmates, with the following results
No. Of pets | Frequency |
0 | 4 |
1 | 12 |
2 | 8 |
3 | 2 |
4 | 1 |
5 | 2 |
6 | 1 |
Solution
x | f | Fx |
|
|
|
0 | 4 | 0 | -1.8 | 3.24 | 12.96 |
1 | 12 | 12 | -0.8 | 0.64 | 7.68 |
2 | 8 | 16 | 0.2 | 0.04 | 0.32 |
3 | 2 | 6 | 1.2 | 1.44 | 2.88 |
4 | 1 | 4 | 2.2 | 4.84 | 4.84 |
5 | 2 | 10 | 3.2 | 10.24 | 20.48 |
6 | 1 | 6 | 4.2 | 17.64 | 17.64 |
| 30 | 54 |
|
| 66.80 |
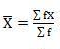
Mean = 54/30 = 1.8
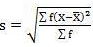
SD = √66.80/30 = 1.49
Standard deviation in grouped data
Direct method
Example 3 –
C.I. | 0 - 2 | 3 - 5 | 6- 8 | 9-11 | 12-14 | 15 -17 | 18 - 20 |
F | 1 | 3 | 5 | 7 | 6 | 5 | 3 |
Solution
C.I | f | Mid point x | Fx | d | 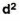 | Fd2 |
0-2 | 1 | 1 | 1 | -10.1 | 102.01 | 102.01 |
3-5 | 3 | 4 | 12 | -7.1 | 50.41 | 151.23 |
6-8 | 5 | 7 | 35 | -4.1 | 16.81 | 84.05 |
9-11 | 7 | 10 | 70 | -1.1 | 1.21 | 8.47 |
12-14 | 6 | 13 | 78 | 1.9 | 3.61 | 21.66 |
15-17 | 5 | 16 | 80 | 4.9 | 24.01 | 120.05 |
18-20 | 3 | 19 | 57 | 7.9 | 62.41 | 187.23 |
| 30 |
| 333 |
|
| 674.70 |
Mean = 333/30 = 11.1
SD =
= 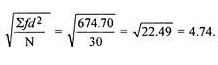
Shortcut method
C.I | f | Mid point x | d(X-AM) | Fd | Fd2 |
0-2 | 1 | 1 | -9 | -9 | 81 |
3-5 | 3 | 4 | -6 | -18 | 108 |
6-8 | 5 | 7 | -3 | -15 | 45 |
9-11 | 7 | 10 | 0 | 0 | 0 |
12-14 | 6 | 13 | 3 | 18 | 54 |
15-17 | 5 | 16 | 6 | 30 | 180 |
18-20 | 3 | 19 | 9 | 27 | 243 |
| 30 |
|
| 33 | 711 |
Assumed mean = 10
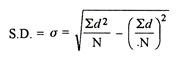
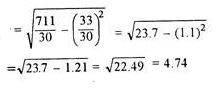
Step deviation method
C.I | f | Mid point x | d | Fd | Fd2 |
0-2 | 1 | 1 | -3 | -3 | 9 |
3-5 | 3 | 4 | -2 | -6 | 12 |
6-8 | 5 | 7 | -1 | -5 | 5 |
9-11 | 7 | 10 | 0 | 0 | 0 |
12-14 | 6 | 13 | 1 | 6 | 6 |
15-17 | 5 | 16 | 2 | 10 | 20 |
18-20 | 3 | 19 | 3 | 9 | 27 |
| 30 |
|
| 11 | 79 |
Here, d is calculate as (X –AM)/i, where i is length of class interval
d = (1 -10)/3 = -3 and so on
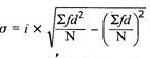
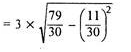
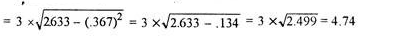
Coefficient of standard deviation
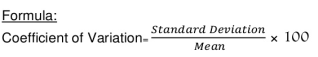
Coefficient of SD = (4.74/11.1)*100 = 42.70
Example 4 – calculate the standard deviation using the direct method
Class interval | Frequency |
30 – 39 | 3 |
40 – 49 | 1 |
50 – 59 | 8 |
60 – 69 | 10 |
70 – 79 | 7 |
80 – 89 | 7 |
90 – 99 | 4 |
Solution
Class interval | Frequency | Mid point x | Fx |
|
|
|
30 – 39 | 3 | 34.5 | 103.5 | -33.5 | 1122.25 | 3366.75 |
40 – 49 | 1 | 44.5 | 44.5 | -23.5 | 552.25 | 552.25 |
50 – 59 | 8 | 54.5 | 436.0 | -13.5 | 182.25 | 1458 |
60 – 69 | 10 | 64.5 | 645.0 | -3.5 | 12.25 | 122.5 |
70 – 79 | 7 | 74.5 | 521.5 | 6.5 | 42.25 | 295.75 |
80 – 89 | 7 | 84.5 | 591.5 | 16.5 | 272.25 | 1905.75 |
90 – 99 | 4 | 94.5 | 378.0 | 26.5 | 702.25 | 2809 |
| 40 |
| 2720 |
|
| 10510 |
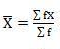
Mean = 2720/40 = 68
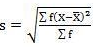
SD = √10510/40 = 16.20
Example 5 - calculate the mean and standard deviation of hours spent watching television by the 220 students.
Hours | No. Of students |
10 – 14 | 2 |
15 – 19 | 12 |
20 – 24 | 23 |
25 – 29 | 60 |
30 – 34 | 77 |
35 – 39 | 38 |
40 - 44 | 8 |
Solution
Hours | No. Of students | x | Fx |
|
|
|
10 – 14 | 2 | 12 | 24 | -17.82 | 317.49 | 634.98 |
15 – 19 | 12 | 17 | 204 | -12.82 | 164.31 | 1971.67 |
20 – 24 | 23 | 22 | 506 | -7.82 | 61.12 | 1405.85 |
25 – 29 | 60 | 27 | 1620 | -2.82 | 7.94 | 476.53 |
30 – 34 | 77 | 32 | 2464 | 2.18 | 4.76 | 366.55 |
35 – 39 | 38 | 37 | 1406 | 7.18 | 51.58 | 1959.98 |
40 - 44 | 8 | 42 | 336 | 12.18 | 148.40 | 1187.17 |
| 220 |
| 6560 |
|
| 8002.73 |
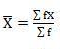
Mean = 6560/220 = 29.82
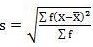
SD = √8002.73/220 = 6.03
Merits
- It takes into account all the items and are used for future statistical analysis
- It is suitable for making comparison
Demerits
- It is difficult to compute
Key takeaways –
- Dispersion measures the scatteredness of the data series around its average.
Sources
- I.B. N. Gupta : Business Math & Statistics
- II. S. P. Singh : Statistics
- III. Mukund Lal : Statistics
- IV. K. N. Nayar : Statistics
- V. C. B. Gupta : Statistics
- VI. Shukla & Sahay : Statistical Analysis
- VII. C. D. Gupta : Statistical Analysis
- VIII. D. N. Elhana : Statistical Analysis
















