Unit - 1

Foundation

1.1 Atomic Structure

(a) Features of H-spectra

Electrons present in a molecule or atom get excited on absorption of energy, they jump from a lower energy to a higher energy level and emit radiations when they return to their original state. This phenomenon is related to the emission spectrum through hydrogen too better known as hydrogen emission spectrum.

In 1800, when gases are excited with an electric charge and the resulting light emitted is viewed through diffraction grating, the spectrum formed consists not of a continuous band of light, but of individual lines with well-defined wavelengths. Experiments have shown that the wavelengths of the lines were characteristic of the chemical element emitting the light. They were an atomic fingerprint which resulted from the internal structure of the atom.

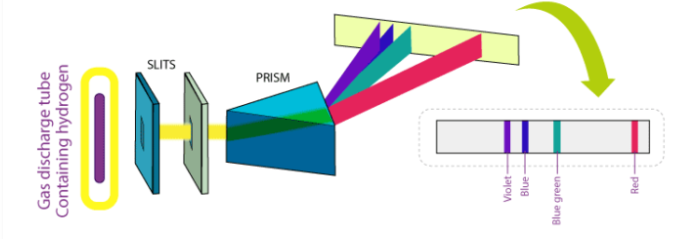
Fig 1: The spectrum of Hydrogen

The spectrum of hydrogen is an important piece of proof to show the quantized structure of an atom. The hydrogen atoms of the molecule dissociate immediately when the electric charge is passed through a gaseous hydrogen molecule It results in the emission of electromagnetic radiation initiated by the energetically excited hydrogen atoms. The hydrogen emission spectrum comprises radiation of discrete frequencies. These series of radiation are named after the scientists who discovered them.

When a hydrogen atom absorbs a photon, it causes the electron to experience a transition to a higher energy level, for example, n = 1, n = 2. When a photon is emitted through a hydrogen atom, the electron undergoes a transition from a higher energy level to a lower, for example, n = 3, n = 2. During this transition from a higher level to a lower level, there is the transmission of light occurs. The quantized energy levels of the atoms, cause the spectrum to comprise wavelengths that reflect the differences in these energy levels. For example, the line at 656 nm corresponds to the transition n = 3 n = 2.

Hydrogen emission spectrum:

In 1885 Balmer, on the basis of experimental observations proposed a formula to correlate the wave number of the spectral lines emitted and the energy shells involved This formula is given as:

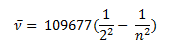
The series is called Balmer series, that involves the hydrogen emission spectrum, which is the only series of lines in the electromagnetic spectrum that lies in the visible range. The value, 109,677 cm-1, is called the Rydberg constant for hydrogen. The Balmer series is basically the part of the hydrogen emission spectrum responsible for the excitation of an electron from the second shell to any other shell. Similarly, other transitions also have their own series names. Some of them are listed below,

Fig 2: Hydrogen emission spectrum

Johannes Rydberg, a Swedish spectroscopist, derived a general formula for the calculation of wave number of hydrogen spectral line emissions due to the transition of an electron from one orbit to another. The general formula for the hydrogen emission spectrum is given by:

Where,

n1 = 1,2,3,4 …

n2 = n1 +1

ν= wave number of electromagnetic radiations. The value 109,677 cm-1 is known as Rydberg constant for hydrogen.

Bohr model of the hydrogen atom was the first atomic model to successfully explain the radiation spectra of atomic hydrogen. Niels Bohr introduced the atomic Hydrogen model in the year 1913. Bohr Model of the hydrogen atom attempts to plug in certain gaps as suggested by Rutherford’s model. It holds a special place in history as it gave rise to quantum mechanics by introducing the quantum theory.

Bohr's interpretation of H-spectra and limitation

Planetary Model of the Atom

Quantum mechanics emerged in the mid-1920s. Neil Bohr, one of the founders of quantum physics, showed much interest in the structure of the atom. Numerous atomic models, including the theory postulated by J.J Thompson and the discovery of nucleus by Ernest Rutherford had emerged. But Bohr supported the planetary model, which asserted that electrons revolved around a positively charged nucleus just like the planets around the sun.

Fig 3: Planetary Model of The Atom

Bohr’s Equation

The model proposed by Bohr on hydrogen atom, had first proposed about the planetary model, later concern about electrons were assumed. The assumption was based on the quantization of the structure of atoms. According to Bohr the electrons orbited around the nucleus in specific shells or orbits having a fixed radius. The shells only that had radius which was provided by the equation were permitted and it was difficult for the electrons to be present between the shells.

Mathematically, the allowed value of the atomic radius is given by the equation:

r(n)=n2×r(1)

Where,

The Bohr’s radius has a value of: r(1)=0.529×10−10m.

Bohr calculated the energy of an electron in the nth level of hydrogen by considering the electrons in circular, quantized orbits as:

E(n)=−1n2×13.6eV

Where,

13.6 eV is the lowest possible energy of a hydrogen electron E(1).

The ground state is n=1, and the energy that is obtained is a negative number always, as the energy of an electron in the orbit is relative to the energy that is completely separated from its nucleus, n=∞ and it is recognised to have an energy of 0 eV. Since the electron in a fixed orbit around the nucleus is more stable than an electron that is extremely far from its nucleus, the energy of the electron in orbit is always negative.

Absorption and Emission

According to Bohr’s model, the electrons absorb energy that are in the form of photons and get excited to higher energy levels, after the electron escapes to the higher energy level also known as the excited state, the excited electrons are however less stable and would immediately emit an electron to come back to the lower and more stable energy level. The energy of the emitted photon is equal to the difference in energy between the two energy levels for a specific transition. The energy can be calculated using the equation

hv=ΔE=(1n2low−1n2high)13.6eV

Fig 4: Atomic Excitation and De-excitation

Limitations of the Bohr Model of the Hydrogen Atom:

Postulates of Bohr’s Model of an Atom

Refinement of Bohr theory

Hydrogen atoms are known to have less protons in nucleus compared to the heavier atoms, therefore more electrons are necessary to cancel the positive charges of these protons. Bohr stated that every electron orbit could only hold a set number of electrons, once the levels were full the electrons they would be bumped to the next level. Thus, the Bohr model for heavier atoms detailed about the electron shells, the model also explained the atomic properties of heavier atoms, that was never explained before, for example, the shell model explained why atoms got smaller moving across a period (row) of the periodic table, even though they had more protons and electrons. However, the model assumed electrons in the shells didn't interact with each other and couldn't explain why electrons seemed to stack in an irregular manner.

The most prominent refinement to the Bohr model was the Sommerfeld model, which is sometimes called the Bohr-Sommerfeld model. In this model, electrons travel in elliptical orbits around the nucleus rather than in circular orbits. The Sommerfeld model was better at explaining atomic spectral effects, such the Stark effect in spectral line splitting. However, the model couldn't accommodate the magnetic quantum number.

Ultimately, the Bohr model and models based upon it were replaced Wolfgang Pauli's model based on quantum mechanics in 1925. That model was improved to produce the modern model, introduced by Erwin Schrodinger in 1926. Today, the behaviour of the hydrogen atom is explained using wave mechanics to describe atomic orbitals.

Bohr-Sommerfeld theory

Bohr succeeded in the calculation of radii and also the energies of the stationary orbit around the nucleus in an atom, and the values were found to correlate well with the experimental values.   He also gave the Hydrogen ion spectrum. For these reasons, however this theory was widely accepted all over the world, as years passed, with the introduction of high resolving spectroscopes, studies revealed very fine spectral lines which Bohr was not able to explain, from this point Sommerfeld extended Bohr theory and gave his postulates.

According to him, the stationary orbits inside which the electrons revolve around the nucleus in the atom are not circular in shape but is elliptical., which is due to the influence of the centrally located nucleus.in this elliptical path the electron with nucleus moves at one of its foci, therefore there will be a major and minor axis of the path. According to him, as the orbit broadens the length axis approach to an equal value and finally become equal i.e., the path become circular. So, we can say the circular path is just one special case elliptical path.

As the electrons pass in this elliptical path., it shows an angular moment which must be quantised according to the quantum theory of radiation

 Bohr gave that angular momentum as m=nh/2Ω but Sommerfeld used another integer k instead of n. k is an integer known as azimuthal quantum number. n used by Bohr and k used by Sommerfeld are related as: –

n/k = length of major axis/length of minor axis

With increase in value of k, the path becomes more and more elliptical and eccentric. When k=n, the path becomes circular.

Bohr did not succeed in explaining the fine spectral lines visible by high revolving power spectroscopes but Somerfield was successful in explaining this concept. According to Somerfield the energy of the stationary orbit depends not only on ‘n’ but also on ‘k’ to a certain extent., therefore when a transition from a higher level to lower level occurs, there would be more than one value for ‘k’, and different from the theory of Bohr, therefore Sommerfeld was successful in explaining the reason for the occurrence of spectral fine lines. Even the frequencies of some of those fine spectral lines came to be in well agreement with the frequencies by Sommerfeld.

Sommerfeld theory is also sometimes referred to as Bohr-Sommerfeld theory.

(b) Shapes of orbitals and their labelling’s

Atomic orbitals are mathematical functions that describe the wave nature of electrons (or electron pairs) in an atom.

They offer a way to calculate the probability of finding an electron in a specified region around the nucleus of the atom.

Orbitals Chemistry

There are four different kinds of orbitals, denoted s, p, d and f each with a different shape. Of the four, s and p orbitals are considered because these orbitals are the most common in organic and biological chemistry. An s-orbital is spherical with the nucleus at its centre, a p-orbitals is dumbbell-shaped and four of the five d orbitals are cloverleaf shaped. The fifth d orbital is shaped like an elongated dumbbell with a doughnut around its middle. The orbitals in an atom are organized into different layers or electron shells.

According to the quantum atomic model, an atom can have many possible numbers of orbitals. These orbitals can be categorized on the basis of their size, shape or orientation. A smaller sized orbital means there is a greater chance of getting an electron near the nucleus. The orbital wave function or ϕ is a mathematical function used for representing the coordinates of an electron. The square of the orbital wave function or represents the probability of finding an electron.

The Shape of s Orbitals

An S orbital is spherical symmetrical around the nucleus of an atom like a hollow ball with nucleus at the centre. As the levels of energy increase, the electrons are located further away from the nucleus, so the orbitals get bigger the order of size

is 1s<2s<3s< ------ as shown

Fig 5: The figure shows that as the energy levels increase, the electrons move further away from the nucleus, as a result the orbitals get bigger in size the order of size is 1s<2s<3s<…

The Shape of p Orbitals

Unlike s orbitals, a p orbital points in a particular direction, at any one energy level we have three absolutely equivalent p orbitals pointing mutually at right angles to each other they are given symbols px , py, pz. . The p-orbitals at the second energy level are called 2px, 2py,2pz and so on. All levels except the first energy level have p orbitals.

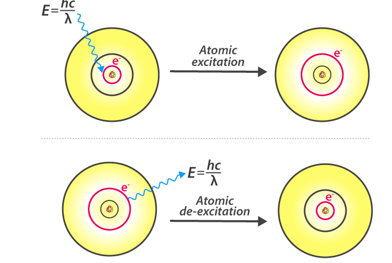
Fig.6: At any one energy level, we have absolutely three equivalent p orbital pointing mutually at right angles to each other,

 They are arbitrarily given the symbols px, py, pz .at any one energy, we have three absolutely equivalent p orbitals pointing mutually at right angles to each other. These are arbitrarily given the symbols px, py, pz, which is for convenience. the p orbitals at the second energy level are called 2px,2py,2pz. there are similar orbitals at subsequent levels: 3px,3py,3pz….and 4px, p4py,4pz and so on. All levels except the first have p orbitals.

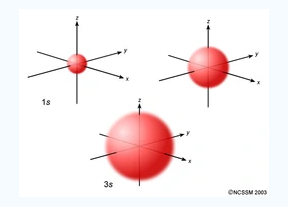
Fig.7: In addition to s and p orbitals, there are two other sets of orbitals which become available for electrons to inhabit at higher energy levels, at the third level, there are an aet of five d orbitals as well as 3s and 3p orbitals, at the third level there are a total of nine orbitals.

The Shape of d Orbitals

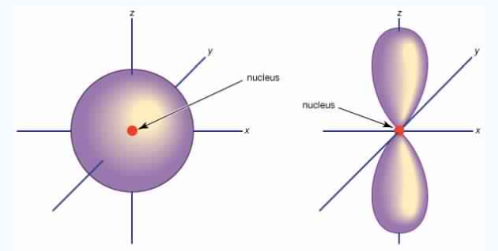
Fig. 8: The first group contains 3dxy,3dxz and3dyz orbitals, the names specify that these orbitals Lie in the x-y plane, the x-z plane and the y-z plane. Each lobe has four lobes and each lobe points between. Two axes and not along them. The second group contains the 3dx2-y2and3dz2 orbitals, these lobes point along various axes the 3dx2-y2 looks exactly like the first group, except that the lobes are pointing along. The x and y axes, not between them. The3dz2 looks like a p orbital:

At the fourth and higher levels there are 7f orbitals in addition to the 4s, 4p and 4d orbitals. Counting the 4s, 4p and 4d orbitals. This makes a total of 16 orbitals in the 4th level.

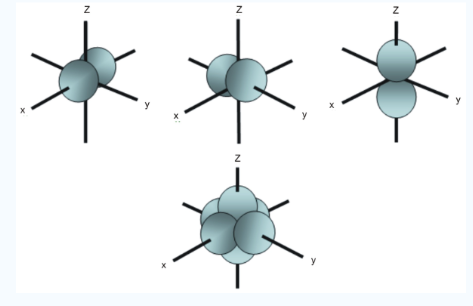
Fig.9:  counting the 4s,4p,4d orbitals, this makes a total of 16 orbitals in the fourth level. The s, p, d and f orbitals are more complicated at higher energy levels.

Idea of quantum numbers

Quantum numbers are used to define the trajectory and movement of electron within an atom. Additionally, the quantum numbers of every electron in an atom are combined, it should obey the Schrodinger equation.

Quantum number is a value, which is used to describe the energy available in atoms and molecules. Moreover, an electron within an ion or an atom has four such numbers to portray its energy state. Additionally, it yields clarifications to the wave equation for hydrogen atoms by Schrodinger. These four quantum numbers are –

Furthermore, every electron in an atom has a set of unique quantum numbers. According to the ‘Pauli exclusion principle’, these four quantum numbers and their combination cannot be the same in two electrons.

Additionally, these quantum numbers are crucial, as they are used to comprehend the electron configuration of an atom. Besides, they also give an idea of the possible location of an atom’s electrons. Moreover, the significance of quantum number is that it is useful to gather information on characteristics of atoms like its radius, and ionisation energy.

Values of Quantum Numbers

As mentioned above, the ‘Pauli exclusion principle’ mentions that two electrons within an atom cannot have similar sets of quantum numbers. Hence, every number has either an integer or a half-integer value. Therefore, the values of these quantum number are –

Principal Quantum Number

This principal quantum number portrays the electron shell or energy level of an atom. Here, the value of ‘n’ starts from one and gradually increases to the shell that contains the outermost electron of particular atom. For instance, in caesium (Cs), the outmost valence electron within the shell has energy level 6. Hence, the ‘n’ value of an electron in caesium can range from 1 to 6.

Moreover, particles that are in a time-independent potential have nth eigenvalue of Hamiltonian, as per the Schrodinger equation. Hamiltonian’s nth eigenvalue refers to the energy, i.e., E with contribution from angular momentum. However, the term that involves J2 is not considered here.

Therefore, this number only depends on the distance between an electron and its nucleus, which is the radial coordinate ‘r’. Since the average number rises with ‘n’, quantum states with various principal quantum numbers are said to be a part of different shells.

Azimuthal Quantum Number

The azimuthal quantum number is commonly known as the angular of orbital quantum number. Moreover, it describes the subshell of an electron and its magnitude of the orbital angular momentum via relation. Additionally, in spectroscopy or chemistry where

Therefore, the value of l varies from 0 to n-1, because the first p orbital where l=1 arrives in the second electron shell, i.e., n=2. Likewise, the first d orbital, i.e., l=2, appears within the third shell, which is n=3, and so on. The azimuthal quantum number is very significant in chemistry, as it identifies the shape of an atomic orbital, and has a powerful effect on chemical bonds and bond angles.

Magnetic Quantum Number

Magnetic quantum numbers articulate the energy available in a subshell and estimate the orbital angular momentum along a specific axis. Moreover, values associated with ml ranges between – to l, but integer steps are associated. Additionally, the ‘s’ is a subshell where l=0 has one orbital. Therefore, ml of an electron within a ‘s’ subshell will be zero always.

Additionally, the ‘p’ subshell, i.e., l=1 comprises three orbitals. It is also known as three ‘dumbbell shaped’ clods. Hence, the ml of an electron in this ‘p’ subshell should be either -1, 0,1.

Lastly, the ‘d’ subshell where l=2 has five orbitals. Furthermore, here ml has values starting from -2 to +2. Additionally, the value of ml quantum number here is associated with orbital orientation.

Spin Projection Quantum Number

The fourth number on this list, quantum numbers spin describes intrinsic angular momentum or ‘spin’ of an electron within an orbital. Moreover, it provides a projection of the spin angular momentum(s) along a particular axis.

Additionally, the values of ms r start from -s to s. Here, ‘s’ defines the spin quantum number, an inherent property of particles. An electron that has a spin ‘s’=1/2, its ms will be ‘+/-‘, confirming its spin and opposite spin. Moreover, every electron in any particular orbital should have different spins according to ‘Pauli Exclusion Principle’. Hence, an orbital cannot contain more than 2 electrons.

Background of Quantum numbers

The work of Broglie and Bohr have established how electrons have diverse discrete energy levels associated with their atomic radius. This model offered a comparatively, simpler spherical view. Moreover, this model by Bohr and Broglie indicated how the energy level of electrons is related to their principal quantum number. However, there are no numerical ways present in this model to classify, additional behaviour of an electron in space.

Pauli’s exclusion principle

Pauli exclusion principle states that no two electrons present in a single atom will have an identical set or will have the same quantum numbers (n, l, ml, and ms).in simple terms every electron must have its own unique state (singlet state). There are two salient rules that the Pauli Exclusion Principle follows:

The Pauli’s exclusion principle not only applies to electrons but also applies to half-integer spin such as fermions. It is however not applicable to particles having an integer spin such as bosons having symmetric wave functions. Moreover, bosons can share or have the same quantum states, unlike fermions.

Formulation of the Principle

In the year 1925 an Austrian physicist named Wolfgang Pauli formulated the principle, in the principle basically the behaviour of the electrons was described. In 1940 the principle was expanded to cover the fermions under spin-statistics theorem. Meanwhile, fermions that are described by the principle include elementary particles such as quarks, electrons, neutrinos, and baryons.

Wolfgang Pauli was also awarded the Nobel prize in the year 1945 for the discovery of the Pauli exclusion principle and his overall contribution in the field of quantum mechanics

Pauli Exclusion Principle in Chemistry

In chemistry, Pauli’s exclusion principle was applied to determine the electron shell structure of atoms or to predict which atom may donate electrons, when we look at the atoms whenever it gains a new electron or electrons it usually moves to the lowest energy state or it shifts to the outermost shell. If the state has one electron, then it can either be spin-up or spin down. Now, if we consider the Pauli exclusion principle if there are two electrons in a state, then each of the electrons will have spin-up or spin down-state but not the same.

Pauli Exclusion Principle Example

We can take a neutral helium atom as a common Pauli Exclusion Principle example. The atom has 2 bound electrons and they occupy the outermost shell with opposite spins. Here, we will find that the two electrons are in the 1s subshell where n = 1, l = 0, and ml = 0.

Their spin moments will also be different. One will be ms = -1/2 and the other will be +1/2. If we draw a diagram then the subshell of the helium atom will be represented with 1 “up” electron and 1 “down” electron. In essence, 1s subshell will consist of two electrons, which have opposite spins.

Similarly, if we take Hydrogen, it will have 1s subshell with 1 “up” electron (1s1). Lithium will have the helium core (1s2) and then one more “up” electron ( 2s1).   here is the electron configuration of the orbitals, is depicted and is written in this manner.

Formulation of the Pauli Exclusion Principle

Fig 10: From the above example, we can further deduce that successive larger elements will have shells of successively higher energy.

The number of electrons in the outermost shell is also directly related to the different chemical properties that elements possess. Elements with the same number of electrons in the outermost shell will have similar properties.

Hund’s Rule

According to Hund’s rule:

An electron does not pair with another electron that is present in a half-filled orbital, because the electrons will fill the orbitals with similar energy. In the ground state many in paired electrons are present in atoms. when two electrons come in contact, they would show the same property as that of a magnet. The electrons initially move far away from one another before they pair up.

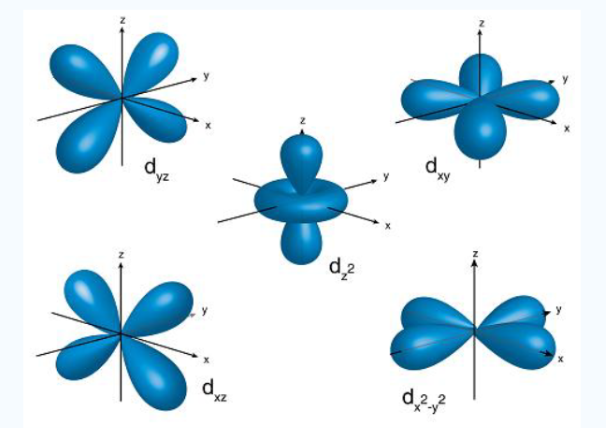
Fig11: Hund’s Rule

Hund’s Rule of Maximum Multiplicity

Hund’s Rule of Maximum Multiplicity rule states that for a given electron configuration, the term with maximum multiplicity falls lowest in energy. According to this rule electron pairing in p, d and f orbitals cannot occur until each orbital of a given subshell contains one electron each or is singly occupied.

State Hund’s Rule

It states that:

1. Every orbital is occupied singly and then later dubbly occupied in the    sublevel.

2. Identical spin is predominant in the electrons that are present in singly occupied orbitals.

Explanation of Hund’s Rule

Before pairing up the electrons enter an empty orbital. As the electrons are negatively charged, they repel each other, therefore the electrons do not share orbitals to reduce repulsion.

When allowing electrons to orbitals, an electron seeks to fill the orbitals with comparable energy (also called as degenerate orbitals) before joining with another electron in a half-filled orbital. Atoms at ground state tend to have as many unpaired electrons, in reflecting this process, consider how many electrons show the same behaviour as the poles on an attraction would, if they came into contact with each other, as the negativity charged electrons fill orbitals, they first try to go as far as possible from each other before matchup.

According to electrons always start with an empty orbital before they jump up, electrons are negatively charged resulting in resistance from each other. Electrons tend to reduce objection by occupying their own orbitals, rather than receiving or accepting an orbital with another electron.

When we consider the second rule, the spins of unpaired electrons in singly occupied orbitals are the same. The initial electrons spin in the sub-level decides what the spin of the other electrons would be. For instance, a carbon atom’s electron configuration would be 1s22s22p2. The same orbital will be occupied by the two 2s electrons although different orbitals will be occupied by the two 2p electrons in reference to Hund’s rule.

Furthermore quantum-mechanical computations have shown that the electrons in only filled orbitals are small adequately or shielded from the nucleus.

For the second principle, unpaired electrons are only filled orbitals have similar spots. Technically the first electron in a sub-shell could be either ‘spin-up’ or ‘spin-down’

Once the spin of the first electron in a subshell is chosen, the spins of all the separate electrons in that sub-shell depend on that first spin.

Hund’s rule of maximum multiplicity

The rule states that, for a stated electron configuration, the greatest value of spin multiplicity has the lowest energy term. It says if two or more than two orbitals having the same amount of energy are unoccupied then the electrons will start occupying them individually before they fill them in pairs. It is a rule which depends on the observation of atomic spectra, which is helpful in predicting the ground state of a molecule or an atom with one or more than one open electronic shell. This rule was discovered in the year 1925 by Friedrich Hund.

Aufbau principle

The Aufbau principle highlights the way in which the electrons are filled in the atomic orbitals of an atom in its ground state. The electrons are filled in the orbitals in the increasing order of the orbital energy level. According to the Aufbau principle the available atomic orbitals with the lowest energy levels are occupied before those of the higher orbitals.

The word ‘Aufbau’ in German means ‘construct’ or ‘build up’. A diagram given below illustrates the order in which atomic orbitals are filled. Here, ‘n’ refers to the principal quantum number and ‘l’ is the azimuthal quantum number.

Fig 12: The Aufbau principle is utilised to can be used to know the location of electrons in an atom and their corresponding energy levels. For example, carbon has 6 electrons and its electronic configuration is 1s22s22p2.

The key factor is that, each orbital can hold a maximum of two electrons (s per Pauli’s exclusion rule) and, the Hund’s rule must be followed for the electrons that are filled in the orbitals of a single subshell. Which means that every orbital in a given subshell must be singly occupied by electrons before any two electrons pair up in an orbital.

Salient Features of the Aufbau Principle

Exceptions

The electro configuration of chromium is [Ar]3d54s1 and not [Ar]3d44s2 (as suggested by the Aufbau principle). This exception is attributed to several factors such as the increased stability provided by half-filled subshells and the relatively low energy gap between the 3d and the 4s subshells.

Fig 13: The energy gap between the different subshells is illustrated below.

Half-filled subshells feature lower electron-electron repulsions in the orbitals, thereby increasing the stability. Similarly, completely filled subshells also increase the stability of the atom. Therefore, the electron configurations of some atoms disobey the Aufbau principle (depending on the energy gap between the orbitals).

For example, copper is another exception to this principle with an electronic configuration corresponding to [Ar]3d104s1. This can be explained by the stability provided by a completely filled 3d subshell.

Electronic configuration of elements

The electron configuration of an atom of any element is the of electrons per sublevel of the energy levels of an atom in its ground state.

How to Determine Electron Configuration

To arrive at the electron configurations of atoms, you must know the order in which the different sublevels are filled. Electrons enter available sublevels in order of their increasing energy. A sublevel is filled or half-filled before the next sublevel is entered.

For example, the s sublevel can only hold two electrons, so the 1s is filled at helium (1s2). The p sublevel can hold six electrons, the d sublevel can hold 10 electrons, and the f sublevel can hold 14 electrons. The common shorthand notation is to refer to the noble gas, rather than write out the entire configuration. For example, the configuration of magnesium could be written [Ne]3s2, rather than writing out 1s22s22p63s2.

Electronic configuration is defined as the distribution of the electrons of an atom into its orbitals according to the rules. This distribution is fixed for every element. Every element has a definite number of protons which its atomic number. The number of electrons is same as the number of protons in an atom. Therefore, we can say that in its neutral state, the atomic number of the element is equal to the number of electrons. The atomic number is the characteristic feature of an atom. The unique distribution of electrons along atomic orbitals is responsible for the element’s specific chemical and physical properties. Therefore, it’s very important to know and study the electronic configuration of all elements.

In order to understand the electronic configuration of elements; it’s important to have a basic understanding of the shells, subshells and orbitals. Filling of the electrons / distribution of the electrons occurs in the atomic orbitals. Different subshells have different number of orbitals. And each shell has a different number of subshells.

Every shell is designated a value which is basically the principal Quantum number, ‘n’. So, for the 1st shell n=1, for the 2nd shell n=2, for the 3rd shell n=3 and so on.

n=1   2   3   4

Shell= K   L   M   N…

The number of subshells in a shell is equal to the value of its principal quantum number and each subshell is designated a value which is called the Azimuthal Quantum number, ‘I’. For instance, for the 1st shell, n=1, so the number of possible subshells is just 1 and the value for ‘I’ is 0. For the 2nd shell, n=2, so the number of subshells is 2 and the value for ‘I’ are 0 and 1. Similarly, it goes further. For every value of ‘I’ we have a corresponding symbol such as:

Value of I=0 1 2 3 4….

Symbol/notation for subshell= s p d f g...

Subshells can have just one orientation or more than one orientation along the coordinate axis in which the electron density can be found and these 3-D spaces around which the probability of finding an electron is maximum is said to be an orbital. In simple words, one subshell can be thought to have just one orbital or more than one orbital for the filling of the electrons. The number of orbitals depends on the value of ‘I’ and each orbital can accommodate a maximum of 2 electrons.

Number of orbitals for a given subshell is equal to: 2l+1. So, in case of 1s (2*0+1=1, 1 orbital only) the subshell itself acts as orbital. Similarly, for 2s, there’s just one orbital and the subshell itself acts as orbital. For 2p, the possible number of orbitals is 3 (2*1+1=3) which are 2px, 2py, 2pz, so the 2p subshell has possible orientations in which electrons can be accommodated i.e., 2p subshell has 3 orbitals and so on.

And as stated earlier, each orbital can accommodate a maximum of 2 electrons. So, 1s can accommodate 2 electrons, 2s can accommodate 6 electrons (3 orbitals*2 electrons each=6 electrons) and so on.

And filling of the electrons for writing the electrons configuration of the elements is done according to the Aufbau rule, Pauli’s exclusion principle and Hund’s rule.

Aufbau rule states that the order of filling various subshells by means of increasing order of energy levels using (n+1) rule. The order of the filling of the orbitals is as follows according to the Aufbau rule/principle:

1s,2s,2p,3s,3p,4s,3d,4p,5s,4d,5p,4f,5d,6p,7s…

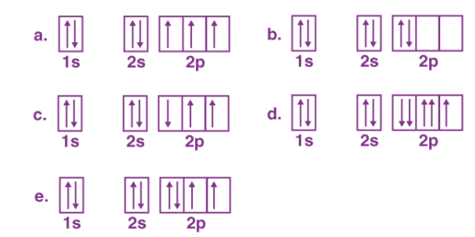
 Fig 14: The Electronic configuration table

1.2 Bonding Models in Inorganic Chemistry

(a) Energetics involved in ionic bond formation

When a metal and nonmetal combine, a transfer of electrons take place: electrons are removed from the metallic element [all electrons from the last electron level] and are gained by the nonmetal [until the octet is completed]

Fig 15: Transfer of electrons

ENERGY INVOLVED IN IONIC BONDS

Oppositely-charged ions attract each other and they form an ionic bond, releasing energy at the same time [exothermic process]. Thus, the energy or enthalpy level of ionic compounds is lower than the isolated ions.

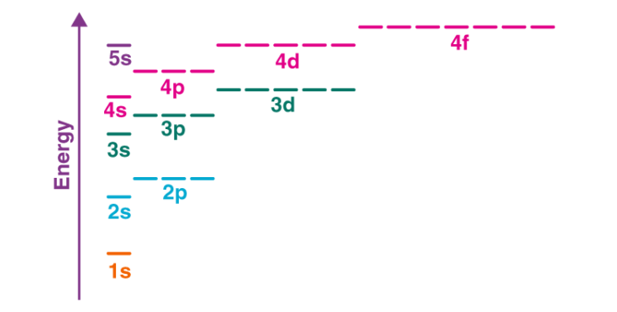
Fig16: Energy in ionic bonds

LATTICE ENERGY

Lattice energy is the enthalpy change when 1 mole of ionic solid is formed. The process of formation of solid crystals is always exothermic.

The value of lattice energy depends [according to Coulomb’s Law] on two main factors: (1) the charge of ions and (2) the size of ions.

A higher value of lattice energy means a higher value of melting point.

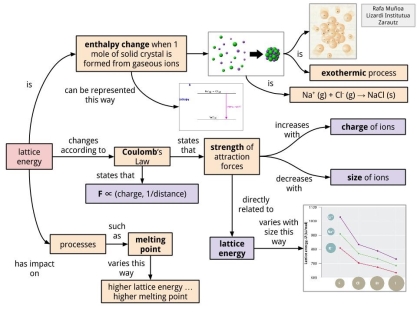
Fig 17: Lattice energy

PROPERTIES OF IONIC COMPOUNDS

Ionic compounds are solids and have high melting points. 

Mechanical properties: brittle

Electric properties: insulators in solid state, conductors when melted or dissolved in water.

It is defined as the amount of energy required to remove the most loosely bound electron from an isolated gaseous atom of an element. The ionization energy of an atom can be considered as a measure to lose an electron and form a cation. The lesser the ionization energy, the grater is the ease of the formation of a cation and thus it can form ionic bond easily.

Alkali metals and alkaline earth metals have low ionization energy; hence they have a tendency to form ionic bonds.

Born Haber cycle

Born Haber cycle also known as the Born Haber process, is a method that is used to analyse and observe energies in a reaction. The cycle mainly assists in describing the formation of ionic compounds from different elements, this methodology enables us to further understand the process by a series of steps.

In 1919, Germain scientists’ names Fritz Haber and max Born introduced the Born-Haber cycle, which is mainly used to calculate the lattice energy. The cycle also involves many steps or processes like electron energy, ionization energy, sublimation energy and the heat of formation and dissociation energy.

Born Haber cycle is a cycle of changes in enthalpy process that leads to the formation of solid crystalline ionic compound from the elemental atoms in their standard state and of the enthalpy of formation of the solid compound such that the net enthalpy becomes zero.

Some important concepts to understand before implementing Born-Haber Cycle are discussed below:

Born Haber Cycle Example

Example: Born Haber cycle of sodium chloride NaCl, (or any AB-type Mono-valent ionic solid).

The heat of formation of sodium chloride (ΔHf0) from the sodium metal and chlorine gas can be experimentally measured.

Na (s) + 1/2​ Cl2 (g) → NaCl(s) ΔHf0 = -411kJ/mol

The formation of ionic solid sodium chloride form solid sodium metal and gaseous chlorine is not a single step process but goes through several processes. Heat changes of all the processes except the lattice energy is a process can be experimentally measured.

The processes or steps in the formation of sodium chloride are-

1. Solid sodium atom sublimes to gaseous atom by absorbing heat energy (∆Hub).

Na (s) → Na (g),

Sublimation energy Hub = + 107kJ/mol

2. Gaseous sodium atom absorbs the ionization energy to release one electron and forms gaseous sodium ion.

Na(g) → Na+(g) + 1e–,

Ionization energy ∆HIE = +502kJ/mol

3. Diatomic gaseous chlorine breaks into two individual atoms by absorbing bond energy, such that each chlorine atom absorbs half of the bond energy of chlorine molecule.

Cl2(g) → 2Cl(g)1/2

Bond dissociation energy of chlorine = 1/2​ ∆Hdiss= 1/2​ 242 = +121kJ/mol

4. Chlorine atom accepts an electron to form chloride ion and releases energy equivalent to electron affinity.

Cl(g) + 1e– → Cl– (g)

Electron affinity = ∆HEA = -355kJ/mol

5. Gaseous sodium ion and gaseous chloride ion combine to form solid sodium chloride molecule and releases energy equivalent to lattice energy.

Na+(g) + Cl– (g) → Na+ Cl– (s)

Lattice energy = ∆HLE = U =?

Summation of enthalpy of all the processes from step 1 to step 5) give the net enthalpy of formation of solid crystalline sodium chloride from sodium and chlorine in their standard conditions of solid and gas respectively. This should be equal to the experimentally measured enthalpy of formation of solid sodium chloride.

The enthalpies are represented as a cycle in the figure.

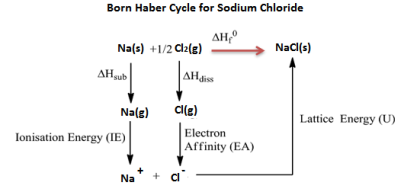
So, ΔHf0 = ΔHsub + ∆HIE +1/2​ ∆Hdis + ∆HEA + U or ΔHf0 – (ΔHsub + ∆HIE + 1/2 ∆Hdis + ∆HEA + U)=0

411 + 107 + 502 +121 -355 +U = 0

Here, except lattice energy, all other enthalpies can be experimentally measured.

Lattice energy of the sodium chloride solid = U = ΔHf0 – (ΔHsub + ∆HIE + ½ ∆Hdis + ∆HEA).

= -411 -107 -502 -121 +355

= – 786kJ/mol

Radius ratio rule

Definition of the Radius Ratio Rule

Radius Ratio is defined as the ratio of smaller ionic radius (cation) to the larger ionic radius (anion). Hence, 

Radius ration ρ = rs/rl.

In matter physis and inorganic chemistry the, the anion -cation radius ratio also known as the Radius ratio Rule is the ratio of the ionic radius of the cation to that of the radius of the anion of the anion in a cation-anion compound.

Radius ratio(r+/r-) Co-ordination no. Limitation:  The radius ratio rule is applicable to the cations and anions that are sphere perfectly, but in many cases the ions or atoms are not perfect sphere, therefore deviations may arise.

What is the significance of radius ratio?

The radius ratio of the ionic solid, is the ratio of the radius of cations (r+) to the radius of the anion (r–).

The significance of radius ratio: The radius ratio is very significant in predicting the structure of the ionic bonds. Greater the radius ratio, greater is the coordination number of cations and anions.

Radius ratio rule states: As the size (ionic radius r) of a cation increases, more anions of a particular size can pack around it. Thus, knowing the size of the ions, we can predict the type of crystal packing.

The Radius ratio rule is useful to predict cation/anion coordination number in any compound therefore it is useful in establishing the structure of solids.

Radius ratio = Radius of cation(r+)

                         Radius of anion (r-)  

Different Type of Crystal Lattice

We already know that solids have basically two shapes, the amorphous solid that has no specific shape the other one is the crystalline solidcrytals, where they have a well-defined structure.

The structure of crystals is made up of a regular arrangement of their atoms, when this arrangement of atoms is represented in a three-dimensional structure it is called a crystal lattice. Therefore, crystal lattice is an array of points in a particular order, that describes the arrangement of particles in a crystalline solid, in simple terms the crystal lattice is the arrangement of atoms in a crystal.

A French scientist found a total of fourteen possible three-dimensional lattices, with six basic shapes. The following diagram shows you the fourteen arrangements.

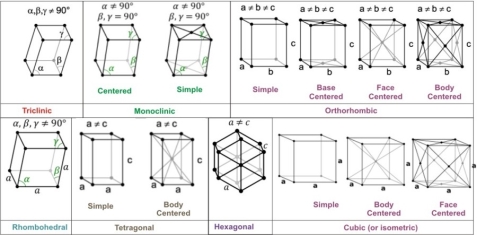
Fig 18: Types of crystal Lattice

Characteristics of Crystal Lattice

Types of Crystal Lattices

There are fourteen types of crystal lattices.

The most popular among them are:

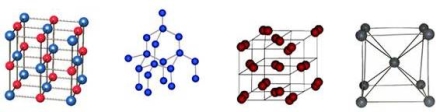
Fig 19: The major four lattices (Ionic , atomic, molecular, metal)

Ionic Lattice

The ionic lattice has the opposite electric charge of ions, that create an electromagnetic field. This lattice also determines the properties of substance with ionic lattice: refractoriness, hardness, density and the ability to conduct electricity. Table salt is a good example of an ionic lattice.

Atomic Lattice

The Atomic lattice have strong covalent bonds in their sites that consist of atoms. Covalent bonds occur when two identical atoms share electrons with neighbouring are also known to form common pair of electrons with neighbouring atoms, this forms he most characteristic feature of the crystal lattice Chemical elements with atomic lattices have a high melting point. Such chemical elements as diamond, silicon, germanium, and boron have atomic lattices.

Molecular Lattice

The molecular lattice shows the presence of stable and closely-packed molecules. These lattices are commonly located in the nodes of the crystal lattice. They are held together by A good example of Molecular lattice is Ice, which is a solid substance that has the property of passing into a liquid matter, the molecular lattice bonds are known to be weak.

Metal Lattice

A metal lattice structure is more flexible and plastic than the ionic one, they look similar to the ionic ones, the metal lattices have a positive charged metal ions in their lattice’s sites. There are electrons present between the nodes that involve in the creation of an electric field. Sometimes these electrons are called electric gas. The metal lattice structure explains its properties: mechanical strength, heat, electrical conductivity, and fusibility.

Fajan's rule

Fajas’ rule predicts whether a chemical bond will be covalent or ionic. A few ionic bonds have partial covalent characteristics which were first discussed by Kazimierz Fajans in 1923. At that time with the help of X-ray crystallography, he was able to predict ionic or covalent bonding with the attributes like ionic and atomic radius.

Postulates of Fajans’ Rule

The rule can be stated on the basis of 3 factors, which are:

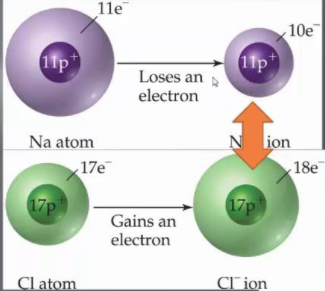
Fig 20: Fajans rule for Ionic and Covalent compounds

Polarising power

It is the extent to which a cation can polarise an anion. It is proportional to charge density. Charge density is the ratio of charge to volume. Polarising power α Charge density. More the charge density, greater is the polarising power for that cation.

Explanation of Fajas’ Rule

Rule 1:

The first rule speaks about the polarising power of the cation. If the cation is smaller, then we can say that the volume of the ion is less. If the volume is less, we can conclude that the charge density of the ion would be high.

Since the charge density is high, the polarising power of the ion would be high. This makes the compound to be more covalent.

Rule 2:

The second rule speaks about the polarizability of the anion. Larger the anion, less is the effective nuclear charge that holds the valence electrons of the ion in place. Since the last electron is loosely bound in large anions, it can easily be polarised by a cation, thereby making the compound more covalent.

Rule 3:

The third rule is a special case. Let us use an example to explain this point.

Example: If we want to find the more covalent compound among HgCl2 and Calcium Chloride we cannot use size as a factor to conclude. This is because both Hg2+ and Ca2+ are of almost equal size. To explain this, we employ the third rule. The electronic configuration of Hg2+ is 6s0 5d10. This configuration is called pseudo-octet because d-orbital is fully filled, but the element does not have 8 electrons or an octet.

We know that d orbitals are not good at shielding, so we can say that the anion (Cl–) would be more polarised because the d orbital is poor at shielding making HgCl2 more covalent than CaCl2 because Ca2+ ion has a noble gas configuration.

Now to answer the question that we asked first, amongst the alkali chlorides, which one is the most covalent?

Since the anion is the same, we have to compare the cations. According to Fajans’ rules, smaller the cation, more is the covalency. Therefore, LiCl is the most covalent.

Inert pair effect

The pnenomena of the two s orbitals not participating in bonding due to high energy that is required for pairing them.

This effect is often considered as a minor effect on the properties of the element; however, it has an extreme importance not only on the element but also on the trends of the periodic table;

The inert-pair effect is known to effect in elements that come after the transition elements in the periodic table. It is the tendency of the outermost s-orbital electrons to not participate in chemical reactions.

The inert pair theory was proposed by Nevil Sidgwick. The theory was first devised to explain the phenomenon of stable +1, +2, +3 and +4 oxidation states in the heavier elements of the 13th,14th,15th and 16th groups of the periodic table. 

Nevil was an English scientist, who was engrossed in explaining the chemical bonding through atomic structure, it was during this study that the inert-pair theory was created.

An alternative explanation was given by Drago, that was based on the M-X bond enthalpies and ionization energies for various oxidation states.

Therefore, the inert-pair effect can be defined as the non-participation of valence shell filled s-orbital electrons in the chemical reactions of the element or the inability of the electrons in the valence shell s-orbital to ionize.

According to Sidgwick the effect occurred due to the sudden rise in the ionization enthalpies of the p-block elements at their second ionization enthalpy.

In 1958 Drago explained the effect by the low M−X bond enthalpies for the heavy p-block elements and the fact that it requires less energy to oxidize an element to a low oxidation state than to a higher oxidation state.

The inert-pair effects were proposed to explain the greater stability of lower oxidation states than the higher oxidation states of heavy p-block elements.

Table 1: Ionization energies of 13th group elements which are influenced by inert-pair effects and lanthanide contraction.

In Table 1, the ∆H₂ in the group of elements in the 13th group is compared and is double compared to ∆H₁.this note was taken as a proof from the inert-pair theory by Sidgwick.

The order of relative stability of +1 oxidation state among 13th group elements: Al< Ga< In< Tl. In the case of Tl, its +1 state is more predominant than the +3 state and Tl⁺³ immediately reduces to form Tl⁺¹. 

Limitations of Inert Pair Effect

There are some limitations of the theory, when we take into consideration the ionizability of electrons or the enthalpy of ionisation of the high value that is expected.

Let us consider the same example of 13th group elements, in order to see some of these limitations.

Table 2: Ionisation enthalpy values of s-orbital electrons.

Generally, the ionisation enthalpy needs to decrease as we go down the group.

But a few anomalies are observed in the table, Increase in ionization enthalpy from Al to Ga and from In to Tl. These examinations couldn’t be described by Sidgwick’s explanation of the inert pair theory. Their simple explanations are Ga’s IE (ionization enthalpy) is affected by d-block contraction and Tl’s relatively high IE is due to relativistic effects caused by poor shielding of d- and f- orbitals.

The latest explanation of the inert-pair theory is:

The 6th row of elements, which is the p-block elements that come after the d-block elements, show poor shielding of d- and f- orbitals, leading to an increase in the nuclear charge effect increase on the valence shell s-orbital electrons thereby tightly holding them and decreasing their participation in bond formation process.

(b) Covalent Bond:

Exceptions to the octet rule

According to the octet rule, atoms are found to be more stable when eight electrons are filled with their valence shells. The rule is applicable only to the main group elements and on observation it is found that the atoms present in the main group elements have the capacity to take part in chemical bonding in a way such that each atom of the resulting molecule has eight electrons in the valence shell.

The elements that obey the octet rule include the s-block elements and the p–block (except hydrogen, helium and lithium) elements, the molecules of oxygen, nitrogen, carbon and halogens also obey the octet rule.

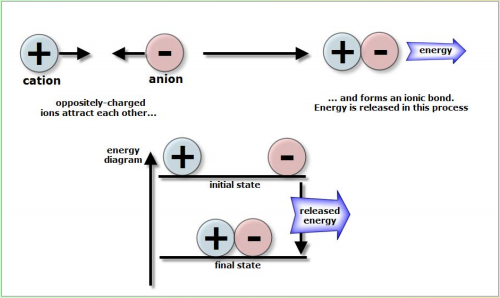
Fig 21: Through the Lewis dot structure, the bonding of oxygen and carbon atoms in a carbon dioxide molecule is shown below

The valence requirement is fulfilled by the share electrons of both the bonded atoms; thus, it can be inferred that both carbon and hydrogen atom have an octet configuration in the CO2 molecule.

Exceptions to the Octet Rule

Not all elements and compounds follow the octet rule. Some of the exceptions to this rule are listed below.

It can be noted that some electron deficient molecules such as boranes and carboranes follow Wade’s rules in order to obtain stability. These molecules feature 3c-2e bonds (three centred bonds) in which two electrons are shared by three atoms.

The exceptions of octet rule fall into three categories: (1) an incomplete octet, (2) odd-electron molecules, and (3) an expanded octet.

Incomplete Octet

In few compounds, the number of electrons that surround the central atom in a stable molecule is less than eight. An alkaline earth metal beryllium is also expected to dorm ionic bonds, but the small size and high ionization energy, comparing to other metals results in beryllium forming primary molecular compounds. As beryllium has only two valence electrons, by sharing electrons they do not form an octet.  The Lewis structure of gaseous beryllium hydride (BeH 2 ) consists of two single covalent bonds between Be and H (see Figure below ).

Figure 22. Beryllium hydride.

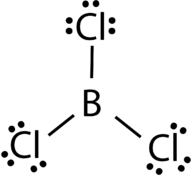
The three valence electrons of Boron and aluminium, form covalent compound with an incomplete octet.  The central boron atom in boron trichloride (BCl 3 ) has six valence electrons as shown in the figure below.

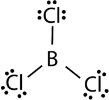
Figure 23. Boron trichloride.

Odd-Electron Molecules

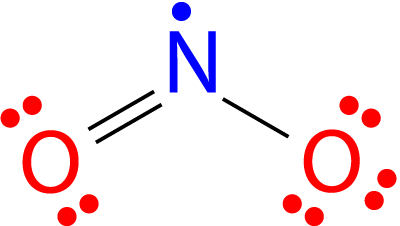
All the atoms in a molecule show the total number of valence electrons as an odd number, therefore they don’t follow the octet rule and becomes impossible for all the atoms of such molecules to follow the rule.  An example is nitrogen dioxide (NO 2).  Each oxygen atom contributes six valence electrons and the nitrogen atom contributes five for a total of seventeen.  The Lewis structure for NO 2 appears in Figure below.

Figure 24. The Lewis structure for nitrogen dioxide, an odd electron molecule.

Expanded Octets

Atoms that are present in the second period, can’t have more than eight valence electrons around the central atom. Consequently, the third period have the tendency to obtain more than eight electrons around the central atom, therefore they exceed the octet rule.in the third group period the d sublevel is available therefore it is possible to use these orbitals in bonding, that results in an expanded octet.

The two elements that react with halogen elements to form stable compounds with expanded octets are Phosphorus and sulphur. The central phosphorus atom of phosphorus pentachloride forms five single bonds to chlorine atoms, resulting in ten electrons that surround it, the central sulphur atom in Sulphur hexafluoride possesses twelve electrons from its six bonds to fluorine atoms.

Figure 25. Phosphorus pentachloride. Left image: Lewis’s structure Right image: molecular model.

Figure 26. Sulfur hexafluoride. Left image: Lewis structure Right image: molecular model.

Idea of orbital overlap

It is known to us that atoms are the results of creation that occurs due to the collision with each other. However, this is just the understanding of the concept at its base level; there’s something more than just collision; things are different at the atomic level.

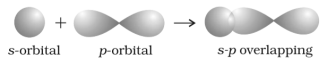
Fig 27: Overlapping of Orbitals

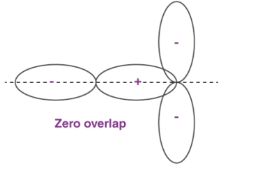
The concept of orbital overlap concept revolves around the process in which any two given atoms come so close to each other that they lose the control over their revolutions and penetrate each other’s orbital, forming a new hybridized orbital. However, here the new result is a bonding pair of electrons. The resultant hybridized orbital, yet, have a lower energy level when compared to the likes of atomic orbital, making it stable. Further, it is at this minimum energy state that the collided atoms release partial penetration, known as atomic orbital overlap.

The extent of molecular orbital overlap is limited to two factors, mainly, the two atoms that have participated in the reaction, their overall size and the valency of the given electrons.

In general, the broader the overlap, the stronger is the resultant bond that is formed between the two atoms. Thus, as per the concept of the orbital concept of a covalent bond, atoms are the result of a combination of overlapping due to their orbital, creating a source for a lower energy state where their valence electrons will spin in the opposite direction and pair up to form covalent bond.

Directional Properties of Bond

The orbital overlap model of molecular bond angles is explained over the simple concept of directional properties of a suggested bond. When the first round of hit occurs over the overlap model, a molecule of hydrogen is formed, as a result of the pi bond overlap of the 1s orbital in the head-on collision. Further, let’s understand the definition of orbital overlap.

Orbital Overlap Definition

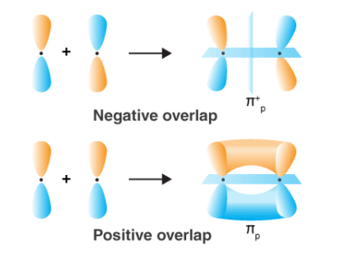
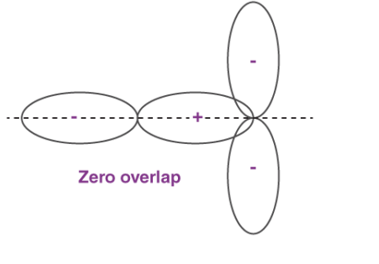
When two atoms come in closer contact, forming a resultant bond between each other, the results of the pi bond overlap can be a consequent number of factors. To begin with, the overlap of the resultant function can either be positive, negative or even give resulting power of zero, depending on the given phase and sign of the two interacting orbitals.

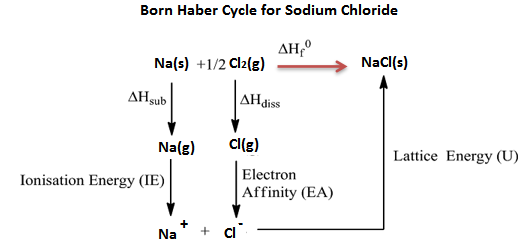
Fig 28 : Types of over lapping

Hybridization of Orbitals

It is a process of mixing two atomic orbitals with the same energy levels to form a degenerated new type of orbital, quantum mechanics is involved in intermixing, the atomic orbitals having the same energy are involved in hybridization, also half-filled and fully filled orbitals can be involved in hybridization, if they have equal energy.

The mixing process in hybridization of atomic orbitals with similar energy are mixed together, the mixing can happen between, two ‘s’ orbitals or two ‘p’ orbital’s or mixing of an ‘s’ orbital with a ‘p’ orbital or ‘s’ orbital with a ‘d’ orbital

The energy is redistributed in the orbitals of the individual atoms to form orbitals of equivalent energy, by the combination of two atomic molecules to form a hybrid molecule and the process is called hybridization. The new orbitals thus formed are known as hybrid orbitals.

Key Features of Hybridization

Based on the nature of the mixing orbitals, the hybridization can be classified as,

Hybridization can be summarized as

For example- here the sp hybrid atomic orbital is formed:

Fig.29: In picture, an atomic orbital can interact with other atoms and overlap resulting in a hybrid atomic orbital. The picture shows an sp hybrid orbital formed.

(c) Van der Waal's forces

In simple words, Van Der Waals Forces are those bonds that play the role of attracting both molecules and atoms. These interactions include weak electrostatic forces lying in a close range within molecules lacking charges. Moreover, they are the weakest intermolecular forces, comprising of dipole-dipole and dispersion forces.

As a segment of molecular physics, these forces came into existence from the name of a Dutch Scientist, Johannes Diderik Van Der Waals. In 1873, he first discovered the Van Der Waals bond while working on a theory on real gases.

According to the Van Der Waals forces definition, they are comparatively weaker electrostatic forces that attract uncharged or neutral molecules towards each other in almost all organic liquids, gases and solids.

In solids, these forces hold each other having lower melting points, and are relatively softer than the ones held by ionic or metallic bonds. In comparison to most of the iconic and covalent bods, these interactions do not arise from an electronic bond.

The Van Der Waal forces include attractions within various atoms, resulting from influenced dipoles. However, they also involve a repulsive interaction within molecules, arising from the overlapping of more than two atomic electronic clouds situated closer to each other. Further, they are known as a universal interaction between various particles, divided by mediums of air or vacuum.

Some Van Der Waals forces examples are hydrogen bonding, dipole-dipole interactions and dispersion forces.

Image will be uploaded soon.

Equation of Van Der Waals Bonds

The Van Der Waals equation is a state that shows two properties of gases, such as the excluded volume of real gases and its attractive forces. It gets expressed as:

(P+n2a/V2) (V-nb)=nRT

Where a=magnitude of attraction within molecules/atoms

And, b= excluded volume.

Properties of Van Der Waals

The below pointers show some of the characteristics of Van Der Waals forces.

Types of Van der Waals interaction

Initially there are three types of Van Der Waals forces, these include:

London Dispersion Forces: These bonds are weakest attractive bonds, resulting from temporary and induced dipoles present in various atoms and molecules, they form when electrons present in two adjacent occupy temporary positions. They are also known as dipole-induced dipole attraction

These forces are also responsible for condensation of non-polar substances into liquids. They often freeze into solids when the temperature falls quickly. According to the Van Der Waals definition, these forces depend on the polarization ability of the molecules or atoms.

The dispersion interactions are also present within two molecules, even the polar ones when they are extremely close to each other. The strength of the Waals forces depends on the number of electrons present in the molecule. Moreover, they occur due to the movement of the electrons.

Dipole-Dipole: These interactions result in the attractive forces within the constant dipoles of two polar molecules. Dipoles arise from the differences among the electronegative effect of the atoms near each other. When it occurs, a polar molecule’s partially negative portion interacts with a partially positive portion of another one.

The opposite-charged dipoles have stronger interactions among them. A molecular dipole arises when there is an unequal sharing of electrons within atoms.

A Van Der Waals example of dipole-dipole forces is visible in hydrogen chloride (HCl) as a positive end of an element attracts the negative end of the other.

Hydrogen Bonds: It is a special type of dipole-dipole interaction within hydrogen atoms. They are comparatively much stronger bonds than dipole-dipole interactions and London forces. These forces arise due to the attractive forces within a hydrogen atom, sharing a covalent bond with two highly electronegative atoms, such as N, O and F, etc.

The strength of a hydrogen bond ranges within 4 kJ/mol and 50 kJ/mol. A hydrogen atom in a molecule gets attracted to other N, F and O atoms. However, only N, O and F atoms in one molecule can form hydrogen bonds.

A Van de Waal Force example of hydrogen bonds is the interaction of water molecules.

Factors Affecting the Strength of Van Der Waal

The factors affecting Van Der Waals forces are as follows:

Importance of Van Der Waal Force

There are multiple applications of Van der Waal’s forces in molecular science. Some of these are:

H-Bonding

Hydrogen bonding refers to the formation of Hydrogen bonds, which are a special class of attractive intermolecular forces that arise due to the dipole-dipole interaction between a hydrogen atom that is bonded to a highly electronegative atom and another highly electronegative atom which lies in the vicinity of the hydrogen atom. For example, in water molecules (H2O), hydrogen is covalently bonded to the more electronegative oxygen atom. Therefore, hydrogen bonding arises in water molecules due to the dipole-dipole interactions between the hydrogen atom of one water molecule and the oxygen atom of another H2O molecule.

Here, the location of the bond pair of electrons in the O-H bond is very close to the oxygen nucleus (due to the large difference in the electronegativities of oxygen and hydrogen). Therefore, the oxygen atom develops a partial negative charge (-δ) and the hydrogen atom develops a partial positive charge (+δ). Now, hydrogen bonding can occur due to the electrostatic attraction between the hydrogen atom of one water molecule (with +δ charge) and the oxygen atom of another water molecule (with -δ charge). Thus, hydrogen bonds are a very special class of intermolecular attractive forces that arise only in compounds featuring hydrogen atoms bonded to a highly electronegative atom. Hydrogen bonds are mostly strong in comparison to normal dipole-dipole and dispersion forces. However, they are weak compared to true covalent or ionic bonds.

When a hydrogen atom is linked to a highly electronegative atom in a molecule, the shared paired of electrons are more attracted, therefore this end of electrons become slightly negative while the other end becomes positive slightly. The positive end of one molecule attracts the negative end of the other resulting in a weak bond is formed between them. This bond is called the hydrogen bond.

Due to the hydrogen bonding, the hydrogen atom links the atoms that are electronegative all together, one by the covalent bond and the other by a hydrogen bond. The conditions for hydrogen bonding are:

Examples of Hydrogen Bonding

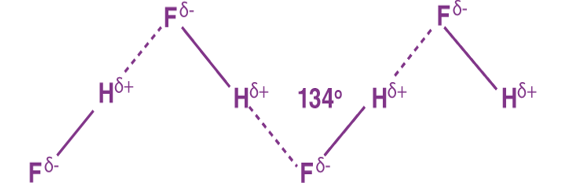
Hydrogen Bonding in Hydrogen fluoride

Fluorine having the highest value of electronegativity forms the strongest hydrogen bond.

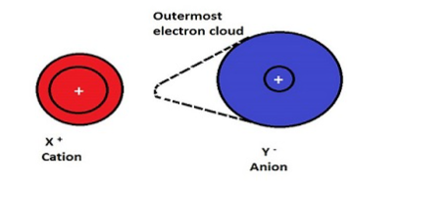
Fig 30: Hydrogen bonding in Flourides

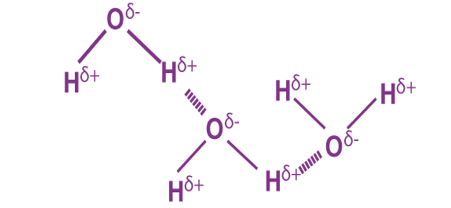
Hydrogen Bonding in Water

A water molecule contains a highly electronegative oxygen atom linked to the hydrogen bond. Oxygen atom attracts the shared pair of electrons more and this end of the molecule becomes negative whereas the hydrogen atoms become positive.

Fig 31: Hydrogen bonding in water

Properties of Hydrogen Bonding

Solubility: the hydrogen bonding that take place between alcohol and water (in lower alcohols)

Volatility: Compounds are less volatile, as they are involved in hydrogen bonding between different molecules, with higher boiling point.

Viscosity and surface tension: Substances exist as associated molecules that consist of hydrogen bonds, therefore the flow becomes difficult comparatively and also results in high viscosity and high surface tension.

Types of Hydrogen Bonding

There are two types of H bonds, and it is classified as the following:

Intermolecular Hydrogen Bonding

When hydrogen bonding occurs between different molecules of the different or same compounds, it is called intermolecular hydrogen bonding.

For example – hydrogen bonding in water, alcohol, ammonia etc.

Intramolecular Hydrogen Bonding

The hydrogen bonding that occurs within the molecule itself is called intramolecular hydrogen bonding.

It takes place in compounds containing two groups such that one group contains hydrogen atom linked to an electronegative atom and the other group contains a highly electronegative atom linked to a lesser electronegative atom of the other group.

The bond is formed between the hydrogen atoms of one group with the more electronegative atom of the other group

1.3 (a) Nomenclature of inorganic Compounds:

Acquaintance with IUPAC use of multiplying affixes

The numerical multiplier (or multiplying affix) in IUPAC nomenclature designates particularly the number of atoms or functional groups that are attached to a particular point in a molecule. These affixes are derived from Greek and Latin.

Compound affixes

The prefixes are the numbers taken from the least significant decimal to the digits upward. units, then tens, then hundreds, then thousands. For example:

548 → octa- (8) + tetraconta- (40) + pentacta- (500) = octatetracontapentacta-

9267 → hepta- (7) + hexaconta- (60) + dicta- (200) + nonalia- (9000) = heptahexacontadictanonalia-

The numeral oneIn organic chemistry, the use of affix mono- is rarely needed, but is very useful in organic chemistry to avoid doubts for example Carbon oxide could be referred as carbon monoxide or carbondioxide. In forming compound affixes, the numeral one is represented by the term hen- except when it forms part of the number eleven (undeca-): hence

241 → hen- (1) + tetraconta- (40) + dicta- (200) = hentetracontadicta-

411 → undeca- (11) + tetracta- (400) = undecatetracta-

The numeral two In compound affixes, the numeral two is represented by do- except when it forms        part of the numbers 20 (icosa-), 200 (dicta-) or 2000 (dilia-).

Icosa- V eicosa

IUPAC prefers the spelling icosa- for the affix corresponding to the number twenty on the grounds of etymology. However, both the chemical abstracts service and the Beilstein database use the alternative spelling eicosa-.

Other numerical prefix types

There are two more types of numerical prefixes in IUPAC organic chemistry nomenclature.

Numerical terms for compound or complex features

Numerical prefixes for multiplication of compound or complex (as in complicated) are created by adding kis to the basic numerical prefix, with the exception of numbers 2 and 3, which are bis- and tris-, respectively.

An example is the IUPAC name for DDT.

Multiplicative prefixes for naming assemblies of identical units

Examples are biphenyl or terphenyl.

Enclosing marks

The basic rules for applying enclosing marks in structural formula are as follows:

      ( ), {( )}, ({( )}), {({( )})}, etc.

The rules needed for ordering the symbols in some of the example formulae below Examples:

 SiH3[SiH2]8SiH3                                       [rule (i)]

 SiH3[SiH2]6SiH(SiH3)SiH3                      [rules (i) and (ii)]

Ca3(PO4)2                                                  [rule (iv)]

 [Co(NH3)6]2(SO4)3                                  [rules (iii), (iv), (vi)]

 [{Rh(µ-Cl)(CO)2}2]                                    [rules (iii), (vi), (vii)]

 K[Os(N)3]                                                  [rules (ii), (iii)]

 (-S-)n                                                            [rule (v)]

  (HBO2)n, or (B(OH)O)n                          [rules (ii) and (v)]

Numbers and Letters

Rule 1: Identification of principal functional groups

First step in writing chemical name for a given b IUPAC is to identify the principal functional group in the structure. If the structure contains only one functional group, it can be directly considered as the principal functional group.

For example

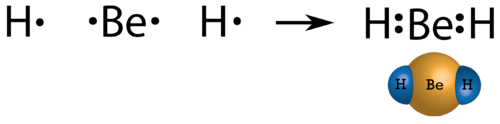
But in many cases compounds will have one functional group. In such cases the

principal group is determined by the priority order. The highest priority is called

the functional group and the rest are called side chains.

Rule 2 Selection of the parent chain

Second task in organic chemistry naming is to select the parent chain. Parent chain can be selected as the longest chain principal functional group.

The longest chain with principal functional group is treated as parent chain.

Note: we must not select a chain without principal functional group as parent chain

even if it’s the longest chain of the compound.

Rule 3: Selection of parent chain from more than one possibility

As we have already seen, a parent chain should be the longest, including principal

functional group. But in few cases, we can observe more than one chain meeting

the above criteria.

It has the longest chains both including the principal functional group, in such situations, we can decide the parent chain by testing the following criteria one after another.

Criteria 1: Chain containing maximun number of funtional groups

Criteria 2:Chain containing maximun number of side chains.

Rule 4: Give the root name

Root name of the compound can be given by counting the number of carbons in the parent’s chain. According to IUPAC nomenclature for organic compounds, root names can be given as follows

Rule 5: Give the numbering

Now we have selected principal functional group, parent chain and root name, next stage of IUPAC nomenclature is to give numbering to the compound in order to identify the location of the side chain

Numbering should be done from that direction which gives least number to the     

principal group

For example

Here the principal functional group is the hydroxyl group(-OH) hence suffix is “ol”. Now numbering can be done from either direction. Numbering from right to left give 2 and left to right give 4 locant to the hydroxyl group, as at least one locant must be possible to principal functional group, the first direction is correct, hence chemical name of the compound is 2-pentanol

Rule 6: Numbering in case of more than one possibility

In case of two or more possibilities, the numbering should be done according to

the following criteria one by one

Criterai 1 : sum of the locants is least (least sum rule)

Criteria 2 : Least number is given to the side chain comed first alphabetically.

Rule 7: The substitution on heteroatom

Atoms other than hydrogen and carbon are considered as heteroatoms. Common

heteroatoms we observe in many of compounds include N, O, S and P etc. When

these atoms are substituted, it should be indicated by corresponding prefix.

Here nitrogen is substituted by methyl groups, hence it should be indicated as N,

N-dimethyl.

Rule 8: Numbering of the side chain

Numbering of the side chain be started from the point of attachment even it bears

any functional group,if sidechain is branched it is again numbered from the carbon

which is attached directly to the parent chain.

Rule 9: Multiple substituents

Substituents or side chains when present more than once on parent chain are represented by prefixes like di,tri,tetra and penta etc

Here chlorine group is present three times at 2,3 and 4 locations. Therfore chemical anme of the compound is 2,3,4-trichloropentane.

Rule 10:Side chains with side chains

Sometimes we find two or more side chains each having further side chains attached in a similar way. In such cases side chains are indicated by terms like bis-,ris-,tetrakis- and pentakis-based on two,three,four and five times they present.

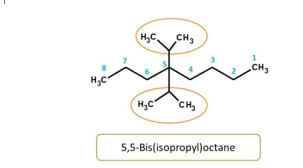
Here again. isopropyl group is attached to main chain in similar way, hence indicated by prefix “bis”

Rule 11: Multiple groups joined by single bond

Generally two identical cyclic groups are joined through a carbon are just indicated as above by the term “di”

But few identical ring systems may be joined directly by single bond wothout any carbon between the two rings. These groups can be indicated by the terms like bi-,ter-, and quarter etc.

Rule 12: Arrangment in alphabetical order

All side chains are arranged alphabetically prefixed by their positions on parent chain

Rule 13: Alphabetical order-includes and excludes

Prefixes are important as they give information of how the groups are connected

to parent chain. While arranging in the alphabetical order by using IUPAC

nomenclature for organic compounds,few prefixes are considered and few are

excluded

Prefixes excluded for alphabetical order:

Names for ions and radicles

Ion

For Ions also the IUPAC nomenclature provides rules.

Hydron

The Generic term for hydrogen cations is Hydron; protons, deuterons and tritons are all hydrons. The hydrons are not found in heavier isotopes.

Parent hydride cations

When a hydron is added to a hydride of a halogen, calcogen or pnictogen, simple cations are formed and are named by adding the suffix "-onium" to the element's root: H4N+ is ammonium, H3O+ is oxonium, and H2F+ is fluoronium. Ammonium was adopted instead of nitronium, which commonly refers to NO2+.

If the cationic centre of the hydride is not a halogen, chalcogen or pnictogen then the suffix "-ium" is added to the name of the neutral hydride after dropping any final 'e'. H5C+ is methanium, HO-(O+)-H2 is dioxidanium (HO-OH is dioxidane), and H2N-(N+)-H3 is diazanium (H2N-NH2 is diazane).

Cations and substitution

Except for methanium, the above given cations are not organic as they don’t contain carbon. However, many organic cations are produced by substituting another element or some functional group instead hydrogen.

The cation name for each substitution is prefixed to its hydride cation name. The name of each substitution is prefixed to the hydride cation name. If many substitutions by the same functional group occur, then the number is indicated by prefixing with "di-", "tri-" as with halogenation. (CH3)3O+ is trimethyloxonium. CH3F3N+ is trifluoromethylammonium.

Naming of Radicals

Radicals are the side chains obtained from the removal of hydrogen from the corresponding hydrocarbon. IUPAC nomenclature for organic compounds considers these radicals as side chains which are indicated by their location on the parent chain.

Radicals can be denoted differently while providing organic chemistry naming based on the number of hydrogens removed from hydrocarbons. They can be univalent, valent or trivalent, if number of carbons removed is one, two or three respectively.

Chemical names of these radicals can be obtained by replacing the suffix “ ane” by the following suffix from the corresponding hydrocarbon.

Isopoly and Heteropoly anions.

Isopoly and heteropoly anions

The groups of VB that are amphoteric metals and also the VIB (chromium, molybdenum and tungsten) that are present in the +5 and +6 oxidation states respectively, produce weak acids that polymerise to form anions that contain many molecules of acid anhydride. If the acids formed consist of only one type of acid anhydride they are called as Is polyacids and their salts are called isopoly salts.

 The acid anhydrides can also condense or polymerise with other acids (e.g., phosphoric or silicic acids) to form heteropoly acids, and their salts are called as heteropoly salts. In the condensation reaction, two wate molecules are eliminated from the weak acid, this occurs reversibly in a dilute aqueous solution, that involves the formation of oxo bridges.

 The best-known and simplest example is the condensation of yellow chromate ion (CrO42−) to form the orange isopoly dichromate ion (Cr2O72−), an equilibrium  reaction the extent of which depends on the pH. In acidic solution the isopoly anion Cr2O72−, predominates while in basic solution the simple ion CrO42− predominates.

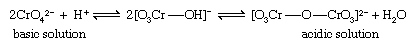
The Heteropoly acids and its salts are produced by coordination of the central atom with ions ranging from four to six anions., which may be mononuclear (containing one metal ion each), as in H7[P(MoO4)6], or trinuclear (containing three metal ions each), as in H3[P(W3O10)4]. Incomplete replacement of oxygen atoms in PO43− ions by MoO3 groups can result in dimers (two-molecule polymers), as, for example, {OP[O(MoO3)3]3}26−.

About 70 elements can act as central (hetero) atoms in heteropoly anions. Because each element may form more than one heteropoly anion and some of these anions can contain several different heteroatoms, thousands of heteropoly acids exist. Heteroatoms may be primary (these atoms are essential to the polyanion structure and thus not susceptible to chemical exchange) or secondary (these atoms can be removed by chemical reaction from the polyanion structure without destroying it). Heteropoly anions can be regarded as coordination compounds with polyanion ligands; e.g., [(H3N)5Cr (OH2)]3+ can be considered the parent of [(SiW11O39)Cr(OH2)]5−.

(b) Acid-Base Chemistry

Bronsted-Lowry definition

In 1923, chemists Johannes Nicolaus Brønsted and Thomas Martin Lowry independently described acids and bases based on whether they donate or accept hydrogen ions (H+). The groups of acids and bases defined in this manner came to be known as either Bronsted, Lowry-Bronsted, or Bronsted-Lowry acids and bases.

A Bronsted-Lowry acid is defined as a substance that gives up or donates hydrogen ions during a chemical reaction. In contrast, a Bronsted-Lowry base accepts hydrogen ions. Another way of looking at it is that a Bronsted-Lowry acid donates protons, while the base accepts protons. Species that can either donate or accept protons, depending on the situation, are considered to be amphoteric.

The Bronsted-Lowry theory differs from the Arrhenius theory is allowing acids and bases that don't necessarily contain hydrogen cations and hydroxide anions

Conjugate Acids and Bases in Bronsted-Lowry Theory

Every Bronsted-Lowry acid donates its proton to a species which is its conjugate base. Every Bronsted-Lowry base similarly accepts a proton from its conjugate acid.

For example, in the reaction:

HCl (aq) + NH3 (aq)→ NH4+ (aq) + Cl- (aq)

Hydrochloric acid (HCl) donates a proton to ammonia (NH3) to form the ammonium cation (NH4+) and the chloride anion (Cl-). Hydrochloric acid is a Bronsted-Lowry acid; the chloride ion is its conjugate base. Ammonia is a Bronsted-Lowry base; its conjugate acid is the ammonium ion.

Solvent system definition

The solvent-based system concept, is based on the Arrhenius theory and draws more attention on the on cation and anion generation in solution

Similar to the Brønsted-Lowry acid-base concept, the solvent system generalises the Arrhenius acid-base concept. According to the Brønsted-Lowry concept looks to generalise the Arhennius acidity in ways that allow all hydrogen ion transfers to be thought of as an acid-base reaction.

H2O(l)+H2O(l)→H3O+(aq)+OH−(aq)

In contrast the Solvent system concepts looks at the Arhennius acidity by focusing on cations and anions generated in any solvents that autoionizes. These include Brønsted-Lowry type autoionizations:

2NH3(l)⇌NH+4+NH−2

2H2SO4(l)⇌H3SO+4+HSO−4

However, the solvent system definition also allows for autoionizations which involve the transfer of an ion other than hydrogen. For example,

2SeOCl2(l)⇌SeOCl++SeOCl−3

2BrF3(l)⇌BrF+2+BrF−4

However, solvent system does not consider acidity in terms of ion transfer, but similar to the Arrhenius concept, the solvent system considers the acids and bases in terms of the effect of the acid and base on the concentrations of cations and anions in solution.

This means that under the solvent system definition:

Note that in the solvent system concept salts of the solvent cation are acids and salts of the solvent anion are bases. For instance, if a salt of BrF−4BrF4− such as sodium tetraflourobromae (NaBrF4NaBrF4) is added to BrF3(l)BrF3(l) the concentration of BrF−4BrF4− increases.

The Solvent System Concept

1. The solvent system definition collapses to the Arrhenius definition for Brønsted acids in water. For instance, HCl is an acid in water since it increases the concentration of H+3H3+ when it dissociates:

HCl(aq)+H2O(l)→H3O+(aq)+Cl−(aq)

2. The solvent system broadens the Arhennius definition by allowing for similar reactions in a variety of solvents. For instance, HClHCl also acts as an acid in liquid ammonia since it gives NH+4NH4+ ion on dissociation.

HClacid+NH3(l)→NH+4+Cl−

Antimony pentaflouride acts as an acid in liquid BrF3 since it abstracts a fluoride to give BrF+.

SbF5acid+BrF3(l)⇌SbF−6+BrF+2

In contrast the fluoride ion of potassium fluoride acts as a base since it adds to BrF3 to give BrF−4.

KFbase+BrF3(l)⇌K++BrF−4

3. The solvent system definition also allows for acid-base neutralization reactions. An example would be the reaction between KF and SbF5 in BrF_3.

KFbase+SbF5acid→KSbF6

4. The solvent system concept allows for successive ionizations just as the Brønsted-Lowry system does. Acids like phosphoric acid can be described well under the Arhennius, Brønsted-Lowry, and solvent system definitions.

2H2SO4⇌H3SO+4+HSO−4

HSO−4+H2SO4⇌H3SO+4+SO2−4

but the solvent system definition also describes the autoionization of nonrpotic solvents like thionyl chloride, SOCl2:

SOCl2(l)⇌SOCl++SOCl−3

SOCl++SOCl2(l)⇌SO2++SOCl−3

Aqua acids

It’s a type of acid, where the acidic hydrogen is present on a water molecule that is coordinated to a metal ion. For example,

Al(OH2)6 3++H2O → Al(OH2)5(OH)2++H3O+

By choosing water molecules at random, let us imagine that the 3+ charge is situated totally on the iron.

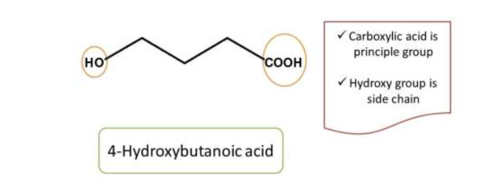
Fig 32: There is a movement of electrons towards the iron, when the lone pairs present on the oxygen form co-ordinate bonds with the iron.

This will show an effect on the electrons in the O-H bonds, which in turn get pulled towards the oxygen more strongly, leaving the hydrogen nuclei more exposed than normal.

The overall effect shows that each of the hydrogen atoms, show more positivity than when it was present in the ordinary water molecules’ 3+ charge is not totally present on the iron but is spread over the whole ion, much of it on the hydrogen atoms.

The effect of dissolving this ion in water

The theory

The hydrogen atoms attached to the water ligands are sufficiently positive that they can be pulled off in a reaction involving water molecules in the solution.

The first stage of this process is:

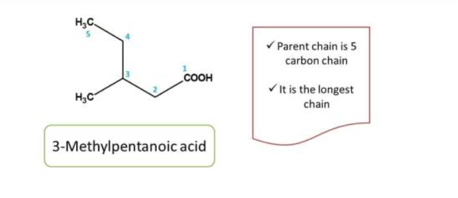
The complex ion is acting as an acid by donating a hydrogen ion to water molecules in the solution. The water is, of course, acting as a base by accepting the hydrogen ion.

Because of the confusing presence of water from two different sources (the ligands and the solution), it is easier to simplify this:

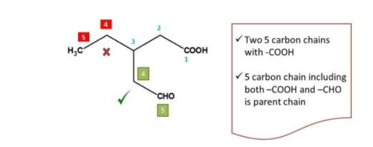
However, if you write it like this, remember that the hydrogen ion isn't just falling off the complex ion. It is being pulled off by a water molecule in the solution. Whenever you write "H+(aq)" what you really mean is a hydroxonium ion, H3O+.

The hexaaquairon(III) ion is quite strongly acidic giving solutions with pH's around 1.5, depending on concentration. You can get further loss of hydrogen ions as well, from a second and a third water molecule.

Losing a second hydrogen ion:

 and a third one:

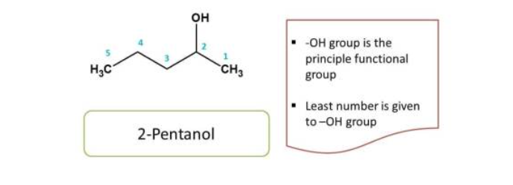
This time you end up with a complex with no charge on it. This is described as a neutral complex. Because it has no charge, it doesn't dissolve in water to any extent, and a precipitate is formed.

Periodic trends in aqua acid strength

The strengths of aqua acids increase with increasing positive charge of the central metal ion and with decreasing ionic radius.

Ionic model: for s -block and early transition metals M

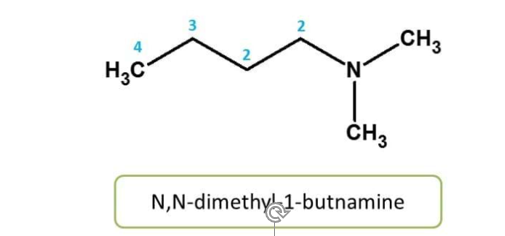
Fig 33: Periodic trends in aqua acid

The strengths of aqua acids increase with increasing positive charge of the central metal ion and with decreasing ionic radius.

Covalent model: for the later d-block and p-block metals

Fig 33: Covalent model

The strengths of aqua acids increase with increasing positive charge of the central metal ion with decreasing ionic radius

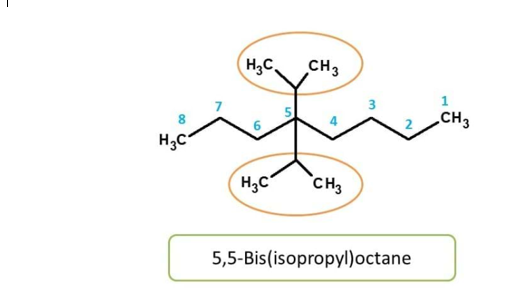
Fig 34: Acidity sequence

HSAB Concept 

Hard and soft Acids and bases (HSAB) principle is a qualitative concept that was explained by Ralph Pearson to explain the stability of metal complexes and the mechanisms of their reactions, here it is also possible to quantify this concept based on Klopman’s FMO analysis using interactions between HOMO and LUMO

According to the principal the Lewis bases and acids can be further divided into soft or hard or borderline types.

The Hard Lewis acids are considered by small ionic radii, high positive charge, strongly salivated and empty valence shell with high energy LUMO

Soft Lewis is categorised by high positive charge, small ionic radii, completely filled atomic orbitals with low energy LUMO

Hard Lewis bases are described by large ionic radii, and low positive charge, completely filled orbitals and low energy LUMO

Soft Lewis bases are characterised by large ionic radii, intermediate electronegativity and highly polarizable, low energy HOMO

The Borderline Lewis acids and bases have intermediate properties

It should be noted it is not essential that Lewis’s acid or base to have all the properties to be classified as hard or soft or borderline.

In short it can be noted that Hard acids and bases are small and non-polarizable, whereas soft acids and bases are large and more polarizable.

1.4 Periodicity

Pauli’s Exclusion principle and periodic table

Pauli exclusion principle states that no two electrons present in a single atom will have an identical set or will have the same quantum numbers (n, l, ml, and ms).in simple terms every electron must have its own unique state (singlet state). There are two salient rules that the Pauli Exclusion Principle follows:

The Pauli’s exclusion principle not only applies to electrons but also applies to half-integer spin such as fermions. It is however not applicable to particles having an integer spin such as bosons having symmetric wave functions. Moreover, bosons can share or have the same quantum states, unlike fermions.

Formulation of the Principle

In the year 1925 an Austrian physicist named Wolfgang Pauli formulated the principle, in the principle basically the behaviour of the electrons was described. In 1940 the principle was expanded to cover the fermions under spin-statistics theorem. Meanwhile, fermions that are described by the principle include elementary particles such as quarks, electrons, neutrinos, and baryons.

Wolfgang Pauli was also awarded the Nobel prize in the year 1945 for the discovery of the Pauli exclusion principle and his overall contribution in the field of quantum mechanics

Pauli Exclusion Principle in Chemistry

In chemistry, Pauli’s exclusion principle was applied to determine the electron shell structure of atoms or to predict which atom may donate electrons, when we look at the atoms whenever it gains a new electron or electrons it usually moves to the lowest energy state or it shifts to the outermost shell. If the state has one electron, then it can either be spin-up or spin down. Now, if we consider the Pauli exclusion principle if there are two electrons in a state, then each of the electrons will have spin-up or spin down-state but not the same.

Pauli Exclusion Principal Example

We can take a neutral helium atom as a common Pauli Exclusion Principal example. The atom has 2 bound electrons and they occupy the outermost shell with opposite spins. Here, we will find that the two electrons are in the 1s subshell where n = 1, l = 0, and ml = 0.

Their spin moments will also be different. One will be ms = -1/2 and the other will be +1/2. If we draw a diagram then the subshell of the helium atom will be represented with 1 “up” electron and 1 “down” electron. In essence, 1s subshell will consist of two electrons, which have opposite spins.

Similarly, if we take Hydrogen it will have 1s subshell with 1 “up” electron (1s1). Lithium will have the helium core (1s2) and then one more “up” electron ( 2s1).   here is the electron configuration of the orbitals, is depicted and is written in this manner.

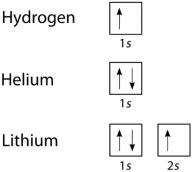
Formulation of the Pauli Exclusion Principle

Fig 6: From the above example, we can further deduce that successive larger elements will have shells of successively higher energy.

The number of electrons in the outermost shell is also directly related to the different chemical properties that elements possess. Elements with the same number of electrons in the outermost shell will have similar properties.

The structure of the periodic table (figure)can be understood in terms of shells and subshells, and, ultimately, the total energy, orbital angular momentum, and spin of the electrons in the atom,

First, the periodic table is arranged into columns and rows. The table is read left to right and top to bottom in the order of increasing atomic number Z. Atoms that belong to the same column or chemical group share many of the same chemical properties. For example, the Li and Na atoms (in the first column) bond to other atoms in a similar way. The first row of the table corresponds to the 1s () shell of an atom.

Consider the hypothetical procedure of adding electrons, one by one, to an atom. For hydrogen (H) (upper left), the 1s shell is filled with either a spin up or down electron (). This lone electron is easily shared with other atoms, so hydrogen is chemically active. For helium (He) (upper right), the 1s shell is filled with both a spin up and a spin down () electron. This “fills” the 1s shell, so a helium atom tends not to share electrons with other atoms. The helium atom is said to be chemically inactive, inert, or noble; likewise, helium gas is said to be an inert gas or noble gas

Fig 35: The periodic table of elements, showing the structure of shells and subshells

The second row corresponds to the 2s and 2p subshells. For lithium (Li) (upper left), the 1s shell is filled with a spin-up and spin-down electron () and the 2s shell is filled with either a spin-up or -down electron, The second row corresponds to the 2s and 2p subshells. For lithium (Li) (upper left), the 1s shell is filled with a spin-up and spin-down electron () and the 2s shell is filled with either a spin-up or -down electron, The process of electron filling repeats in the third row. However, beginning in the fourth row, the pattern is broken. The actual order of order of electron filling is given by

1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s,…

Notice that the 3d, 4d, 4f, and 5d subshells (in bold) are filled out of order; this occurs because of interactions between electrons of an atom

The transition metals are elements in the gap between the first two columns and the last six columns that contain electrons that fill the d (l=1) subshell. As expected, these atoms are arranged in 4l +2=4(2) +2 = 10 columns. The structure of the periodic table can be understood in terms of the quantization of the total energy (n), orbital angular momentum (l), and spin (s). The first two columns correspond to the s (l=0) subshell, the next six columns correspond to the p (l=1) subshell, and the gap between these columns corresponds to the 

d ( l =2)) subshell.

The periodic table also gives information on molecular bonding.

Fundamental trends of atomic/ionic radii, ionization energy, electron affinity, electronegativity, hardness and softness.

Atomic radii or size can be defined in the most simplified manner as the radii

(Or half the "width") of the spherical atoms. Nonbonding atoms have a much larger, more indefinite or "fuzzy" radius, therefore when atomic radius is described as a periodic trend,

the thing that comes to mind is bonding atomic radius.

These are the radii of atoms that are chemically bonded to each another. So, if the bond between two Cl atoms in Cl2 is 1.99 angstroms, resulting in chlorine's bonding atomic radius as about 0.99 angstrom. These values are then used to estimate bond lengths between different elements in molecules.

Atomic radius generally increases from top to bottom down a group.

This generally occurs due to the increase in the principal quantum number, (n).

Therefore, when we go further down a column, the outer electrons move much further away from the atom, making the atom thus larger.

Generally, the atomic radius decreases as we move from left to right across a period.

This occurs mainly due to effective nuclear charge. The greater the effective nuclear charge, the more will be the attraction felt by the outer electrons from the nucleus, and the closer the outer electrons are to the nucleus, making the atom smaller.

Ionic radii are the radii of ions of elements. These distances are based on distances that exist between ions in ionic compounds.

Cations, or positively charged ions, are smaller in size than their "parent" atoms. This is Because cations are formed when the outermost orbitals become empty due to absence of electrons. This also decreases electron-electron repulsions. Therefore, the resulting ions are smaller as there are not as many orbitals that are occupied and the effective nuclear charge affecting the remaining electrons increases, pulling electrons in more closely.  Anions, or negatively charged ions, are larger in size than their "parent" atoms.

This is because of the addition of electrons form these ions, increasing electron-electron repulsions, making the electrons spread out more effectively. Also, effective nuclear charge felt by the outermost electrons decreases. For ions that carry the same charge (i.e., from parent elements of the same group), size increases from top to bottom as we go down a group.

The ionization energy of a chemical category (i.e., an atom or molecule) is the energy required to remove electrons from gaseous ions or atoms. This property is also referred to as the ionization potential and is measured in volts. In chemistry, it often refers to one mole of a substance (molar ionization energy or enthalpy) and is reported in kJ/mol.

 In atomic physics, the ionization energy is typically measured in the unit electron volt (eV).

Atoms or molecules which are larger have lower ionization energy, while smaller molecules or atoms tend to have higher ionization energies.

The ionization energy is not the same for electrons of different molecular or ionic orbitals.

More specifically, the nth ionization energy is the energy required to eliminate the nth

electron after the first n-1 electrons is removed. It is perhaps a measure of the tendency of an ion or atom to surrender an electron or the strength of the electron binding. The greater the ionization energy, the more difficult to remove an electron. The ionization energy may be an indicator to show the reaction of an element. Elements with a lower ionization energy tend to be reducing agents and form cations, and thereby combine with anions to form salts.

Fig.36: This graph shows the first ionization energy of the elements in electron volts(units).

Moving from left to right within a period or upward within a group, the first ionization energy shows an increase. As the atomic radius of an ion or atom reduces, it becomes difficult to remove an electron that is close to a more positively charged nucleus. On the other hand, as one moves down a group on the periodic table, the ionization energy will likely decrease since the valence electrons are far away from the nucleus and experience greater shielding. They experience a weaker attraction to the positive charge of the nucleus.

Ionization energy increases when viewed from left to right in a specific time and decreases from top to bottom in a group.

The ionization energy of an element shows an increase as one move across the periodic Table because the electrons are held together tightly by the highly effective nuclear charge.

This is due to the additional electrons in the same shell do not substantially contribute to shielding each other from the nucleus, however an increase in atomic number corresponds to an increase in the number of protons in the nucleus.

The ionization energy of the elements shows an increase as one moves up a given group because the electrons are held in lower-energy orbitals, closer to the nucleus and thus more tightly bound (which is difficult to remove). The easiest element to ionize is francium and the hardest to ionize is helium respectively. Caesium is said to have the lowest ionization energy and Fluorine is said to have the highest ionization energy

(With the exception of Helium and Neon).

It reflects the ability of an atom to accept an electron. It is the energy change which occurs when an electron is added to a gaseous atom. Atoms with strong effective nuclear charge have greater electron affinity.

The reaction that occurs when an atom takes an electron may be represented as:

X + e− → X− + energy

Another way to define electron affinity is as the amount of energy needed to remove an electron from a singly charged negative ion:

X− → X + e−

Electron Affinity Definition and Trend

Electron Affinity Trend

Electron affinity is one of the trends that can be predicted using the organization of elements in the periodic table.

Electron affinity is more difficult to analyse in molecules because their electronic structure is very complicated. Electron affinity reflects the ability of an atom to accept an electron. It is the energy change which occurs when an electron is added to a gaseous atom. Atoms with strong effective nuclear charge have greater electron affinity.

The reaction that occurs when an atom takes an electron may be represented as:

X + e− → X− + energy

Another way to define electron affinity is as the amount of energy needed to remove an electron from a singly charged negative ion:

X− → X + e−

Electron Affinity Definition and Trend

Electronegativity is the property of an atom which increases with its tendency to attract the electrons of a bond. when two bonded atoms that have similar electronegativity values as each other, they share electrons equally in a covalent bond. Usually, the electrons present in a chemical bond are more attracted to one atom (the more electronegative one) than to the other one. This results in a polar covalent bond. If the electronegativity values are very different, the electrons do not show any sharing. One atom essentially takes the bond electrons from the other atom, forming an ionic bond.

Electronegativity is a property of an atom present within a molecule, rather than an fundamental property of an atom by itself. Thus, electronegativity varies depending on a atom's environment or surroundings. However, most of the time an atom displays similar behaviour in different situations. Factors that affect electronegativity include the nuclear charge and the position and number of electrons in an atom.

Electronegativity Example

The chlorine atom has a higher electronegativity than the hydrogen atom, so the bonding electrons will be closer to the Cl than to the H in HCl molecule.

In the O2 molecule, both atoms have the same electronegativity. The electrons in the covalent  bond are shared equally between the two oxygen atoms.

Hardness and softness of ions is shown on the periodic table below with shading for each of the cells of the table. The table presents hardness and softness of cations and anions as a spectrum, acknowledging that although cations like Mo6+ and U6+ have nominally lost them six outer-shell electrons, they in fact retain some of those electrons, and their large size also makes them softer than a cation like Li1+ that is small and has definitely lost all of its outer-shell electrons. The table also shows compositional trends among minerals containing one cation. The coloured symbols show the results, the harder cations form fluoride, oxide and oxysalt minerals, whereas the softer cations tens more to form sulfide and sulfosalt minerals and the softest cations form bromide, iodide and even bismuthide minerals, therefore we have a clear picture of why some substances exist as minerals andsome do not, harder cations bond well to harder anions and softer cations bond well to softer anions.

First and Second row Anomalies

The elements of 1st and 2nd row show difference in properties with the other elements present in that group. e.g., Hydrogen is different from all the members of 1A group, similarly Li present in same group but show ANOMALOUS behaviour. Similarly, the other head elements of groups I-e Be, B, C, N, O, F show different properties.

Reason:

Why the head elements show anomalous behaviour? this is due to following reasons:
1) They have smallest size in their respective group.

2) High electronegativity than other elements of respective group.

3) High polarizing power.

4) Unavailability of d-orbital.

Anomalous Behaviour of Li:

Idea of ct-orbital participation by non-metals and its influence reactivity

It has been pointed that the elements of the second row (Li to F) not only resemble their heavier congeners to a certain extent (as far as formal oxidation state at least), but also the lower diagonal element (as far as negativity is concerned). For example, both silicon and phosphorus form hydrides that have some properties in common with alkanes, although they are much less stable. As a result of the electronegativity relationship the P-h bond more closely approaches the polarity of the C-H bond than does the Si-H bond. The resemblance of phosphorus to carbon with an example:

In contrast to the inertness of carbon halides, the halides of silicon and phosphorus are extremely reactive with water, to the extent that they must be protected from atmospheric moisture. A clue to the reactivity of these halides is provided by a similar acid halides which readily react with water:

The unsaturation of the carbonyl group provides the possibility of the carbon

Expanding its coordination shell from 3 to 4, thereby lowering the activation energy. Carbon tetrahalide cannot follow a similar path, but the halides of silicon and phosphorus can employ 3d orbitals to expand their octets

The enhanced reactivity of compounds of silicon and phosphorus are typical of all heavier non metals in contrast to elements in second row.

Periodic anomalies of non-metals and post transition of metals

It is generally assumed that the properties of various families of the periodic chart change smoothly from less metallic (or more electronegative).

At the top of the family to more metallic (or less electronegative) at the bottom of the family. Certainly, the extremes of the chart, the alkali metals on the left and the halogens and noble gases on the right, which is true. The ionization potentials for example vary in a rather monotonous way, this is not true for centre parts of the chart, however there is definite tendency for nonmetals of the fourth row, As Se and BR to be unstable in their maximum oxidation state. Although both PCl5 and SbCl5 are stable, the only stable arsenic pentahalide is AsF5: AsCl5 decomposes at -50OC.

In group VIA(16) the same phenomenon is encountered, selenium trioxide is thermodynamically unstable relative to sulfur trioxide and tellurium trioxide.

The enthalpies of formation of SeF6, SF6 and TeF6 are -1210,-1117, and -320kJ Mol-1 respectively, indicating comparable bond energies for S-F and Te-f bonds, which are more stable than Se-F bonds

The best-known exceptions to the general reluctance of bromine to accept a +7 oxidation state are per bromic acid and the per bromate ion, bromine certainly continues the trend started by arsenic and selenium, thus the per bromate ion is a stronger oxidising agent than either perchlorate or periodate.

The tendency for germanium to resemble carbon more than silicon are given in the following examples:

1.Reduction of halides (X) with zinc and hydrochloric acid. Germanium resembles carbon and tin resembles silicon

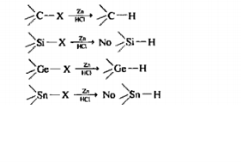
2. Hydrolysis of the tetrahydrides: silane hydrolyses in the presence of catalytic amounts of hydroxide, in contrast, methane, germane and stanine do not hydrolyse even in the presence of large amount of hydroxide ion.

3. Reaction of organolithium compounds with (C6H5)MH, triphenylmethane and triphenyl germane differ in their reaction with organolithium compounds from triphenylsilne and triphenylstannane:

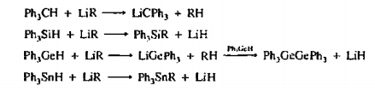
4. Alternatives in Enthalpy formation: there is tendency for the enthalpies of formation of compounds of the group IVA(14) elements to alternate from C-Si-Ge-Sn-Pb. Although closely related to the previous phenomena, this variation is also related to “ inert pair effect”

The elements of group IIIA(14) show similar properties, although in general the differences are not very striking as for Group IVA(14).It may be noted that the covalent radius of gallium appears to be slightly smaller than that of aluminium in contrats to expectation. The first ionization energies of both the elements are close (578 and 579kJ mol-1) and the sum of the first three ionization energies is taken, showing an alternation in the

series: B=6887, Al=5139, Ga=5521, In=5084, TL=5438kJ mol-1

Key take away:

The key feature Of Bohr's theory of spectrum of hydrogen atom is the quantization Of angular Momentum when an electron is revolving around a proton. We will extend this to a general rotational motion to find quantized rotational energy of a diatomic molecule assuming it to be rigid.

The periodic table is structured as an 18 X 7 grid, positioned above a smaller double row of elements. The periodic table only lists chemical elements, and includes each isotope of each element within one cell. In the typical periodic table, each element is listed by its element symbol and atomic number, Covalent compounds usually have a lower boiling and melting point due to the lesser strength of the bond when compared to other bonds like ionic bonds. The covalent bond is directional in nature due to the overlapping of orbitals that are oriented in different directions.

References:

1. Atomic Structure and Chemical Bond, Manas Chanda

2. Atomic Structure, Y.Mido,S.A.Iqbal,M. Satake, M.S Sethi

3. The Periodic Table, Paul Parsons

4. Nomenclature of Inorganic chemistry, Neil.G.Connelly, Richard M Hartshom, Alan T Hutton

5.Principles of Inorganic Chemistry, Brain W. Pfennig