Unit – 1
The States of Matter
Kinetic theory of gases
It is a theoretical model which details the molecular composition of the gas in terms of a huge number of sub microscopic particles that contain both atoms and molecules. Moreover, the theory explains that gas pressure arises due to particles colliding with one another and also the walls of the container. The theory also defines properties such as viscosity, temperature and thermal conductivity and all these properties are related to the microscopic phenomenon.
The importance of the theory is that it provides a developing correlation between the macroscopic and microscopic phenomenon., in simple words the action of molecules is highlighted in the kinetic theory of gases, the molecules of gases are always in motion and tend to collide with each other and also the walls of the container.
Kinetic Theory of Gases Assumptions
Kinetic theory of gases considers the atoms or molecules of a gas as a constantly moving point masses, with huge inter-particle distance and may undergo perfectly elastic collisions. Implications of these assumptions are –
i) Particles
Gas is a collection of a large number of atoms or molecules.
ii) Point Masses
Atoms or molecules making up the gas are very small particles like a point(dot) on a paper with a small mass.
iii) Negligible Volume Particles
The particles are usually far from each other, such that their inner-particle distance is much bigger than the particle. the volume of the particle is negligible to zero compared to volume of the container.
iv) Nil Force of Interaction
The particles present are independent. The particles do not have any attractive of repulsive interactions among them.
v) Particles in Motion
There is constant motion between the particles, due to lack of interactions and free space that is available, the particles show random movement in all directions but in a straight line.
vi) Volume of Gas
Due to the movement of gas particles, they occupy the total volume of container, whether it is small or big, therefore the volume of container to the analysed as the volume of the gases.
vi) Mean Free Path
This is this is an average distance that a particle can travel to meet another particle.
vii) Kinetic Energy of the Particle
As the particles are always in motion, they have an average kinetic energy that is proportional to the temperature of the gas
viii) Constancy of Energy / Momentum
The collision between the moving particles that may collide with each other or other particles of the container, however these collisions do not change the momentum of the particle or the energy.
ix) Pressure of Gas
Collision of the particles on the walls of the container exerts a force on the walls of the container. Force per unit area is the pressure. The pressure of the gas is thus proportional to the number of particles colliding (frequency of collisions) in unit time per unit area on the wall of the container.
Kinetic Theory of Gases Postulates
The kinetic theory of gas postulates is useful in the understanding of the macroscopic properties from the microscopic properties.
Ideal Gas Laws
The laws which deal with ideal gases are naturally called ideal gas laws and the laws are determined by the observational work of Boyle in the seventeenth century and Charles in the eighteenth century.
Ideal Gas Equation
The Ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behaviour of many gases under many conditions, although it has several limitations. The ideal gas equation can be written as
PV = nRT
Where,
According to the Ideal Gas equation-
The product of Pressure & Volume of a gas bears a constant relation with the product of Universal gas constant and the temperature.
i.e., pv=nRT
Universal Gas Constant (R)
When the mass of molecules of any gas is multiplied by its specific gas constant (R), it is observed that the product R is always the same for all gases. This product is called universal gas constant and it is denoted as R.
Note: From the SI system the value of the universal gas constant is 8.314 kJ/mole.K
Derivation of the Ideal Gas Equation
Let us consider the pressure exerted by the gas to be ‘p,’
The volume of the gas be – ‘v’
Temperature be – T
n – be the number of moles of gas
Universal gas constant – R
According to Boyle’s Law,
At constant n & T, the volume bears an inverse relation with the pressure exerted by a gas.
i.e., v∝1p ………………………………(i)
According to Charles’ Law,
When p & n are constant, the volume of a gas bears a direct relation with the Temperature.
i.e., v∝T ………………………………(ii)
According to Avogadro’s Law,
When p & T are constant, then the volume of a gas bears a direct relation with the number of moles of gas.
i.e., v∝n ………………………………(iii)
Combining all the three equations, we have-
v∝nTp
or pv=nRT
where R is the Universal gas constant, which has a value of 8.314 J/mol-K
Deduction of gas laws
All the gas laws may be deduced from equation: PV = 1/3 mnc2 … … (1)
This is the kinetic equation for gases. Although the above deduction has been made for a cubical vessel the equation is valid for a vessel of any shape as the vessel can be divided into a large number of small cubes for each of which this equation is valid.
(a) Boyle’s law: Boyle’s law states the relationship between volume and pressure at constant temperature and mass. Temperature is a measure of the kinetic energy of the molecules. The higher the temperature higher is the kinetic energy of the molecules Equation (1) may be written in the form.
PV = (2/3 x 1/2) mnc2 = 2/3 x total Kinetic Energy … … (2)
Since the kinetic energy of a moving body is – ½ mc2. For a given quantity of gas, when the temperature is constant, the kinetic energy is constant. Hence,
PV = constant (at constant T) which is Boyle’s law. In other words, according to Boyle’s law volume is inversely proportional to pressure when the temperature and the number of molecules is constant.
Charles’ or Gay-Lussac’s law: The total kinetic energy of the molecules is proportional to the absolute temperature. i.e., K.E. = const x T (hence from equation 2)
PV = const x T
In his experiment, he calculated that the increase in volume with every degree equals 1/273.15 times of the original volume. At constant volume for a given quantity of gas P ∞ T., This is Charles’ or Charles’ or Gay-Lussac’s law. According to his findings, at constant pressure and for constant mass, the volume of a gas is directly proportional to the temperature. This means that with the increase in temperature the volume shall increase while with decreasing temperature the volume decreases.
Avogadro’s law: According to Avogadro’s law, at constant temperature and pressure, the volume of all gases constitutes an equal number of molecules. Consider that two gases are at the same pressure, P, and contained in vessels of equal volume, V. Both the vessels are at the same temperature. For the first gas, from the kinetic equation (1)
PV= 1/3 n1m1c12
Where n1 is the number of molecules, m1, is the mass of each molecule and c1 is the r.m.s. velocity. Similarly, for the second gas;
PV = 1/3 n2m2c22
Where n2, m2, and c2 have the same significance as for the first gas. Since P, V and T of the two gases are the same, according to equation (1)
1/3 n1m1c12 = 1/3 n2m2c22 … … … (3)
At the same temperature, the Kinetic Energy of the molecules of both the gases are the same; that is,
1/2 m1c12 = 1/2 m2c22 … … … (4)
If equation (3) is divided by equation (4) One obtains; n1 = n2
That is, the number of molecules in equal volumes of the two gases under the same conditions of T and P is the same. This means that at an unchanged temperature and pressure conditions, the molar mass of every gas is directly proportional to its density. This implies that in unchanged conditions of temperature and pressure the volume of any gas is directly proportional to the number of molecules of that gas. This is Avogadro’s hypothesis or Avogadro’s law.
Calculation of gas constant and kinetic energy
The Gas Constant is the physical constant in the equation for the Ideal Gas Law:
P is pressure, V is volume, n is the number of moles, and T is temperature.
It's also found in the Nernst equation relating the reduction potential of a half-cell to the standard electrode potential:
E is the cell potential, E0 is the standard cell potential, R is the gas constant, T is the temperature, n is the number of mole of electrons exchanged, F is Faraday's constant, and Q is the reaction quotient.
The gas constant is equivalent to the Boltzmann constant, just expressed in units of energy per temperature per mole, while the Boltzmann constant is given in terms of energy per temperature per particle. From a physical standpoint, the gas constant is a proportionality constant that related the energy scale to the temperature scale for a mole of particles at a given temperature.
Units for the gas constant vary, depending on other units used in the equation.
One common value is 8.3145 J/mol·K.
Value of the Gas Constant
The value of the gas constant 'R' depends on the units used for pressure, volume and temperature.
Kinetic energy
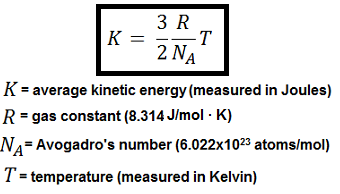
Maxwell Boltzmann distribution Law of Velocities and Energy
The Maxwell-Boltzmann equation, which is based on the kinetic theory of gases defines the distribution of speeds for a gas at a certain temperature. From this distribution function, the most probable speed, the average speed, and the root-mean-square speed can be derived.

If an ideal gas is taken into consideration that is enclosed in a vessel of volume V forming an isolated system, hence total energy ‘u’ of all molecules of the gas remains constant. Let ‘n’ be the molecules in the gas, the energy distribution of these ‘n’ molecules, having total energy ‘u’ enclosed in a volume V in the equilibrium state or most probable state.
We can divide energy u into ‘k’ intervals as u1, u2……...uk let g1, g2………...gk, be the number of cells in energy intervals, u1, u2…….uk respectively. Let n1, n2…...nk be the number of particles in cells g1, g2………. gk respectively. Then the thermodynamics probability of microstate (n1, n2……...nk) is given by
 W= (g1) n1 (g2) n2…………(gk)nk
W= (g1) n1 (g2) n2…………(gk)nk
n1, n2……………nk
Maxwell Boltzmann, distribution curves at different temperatures
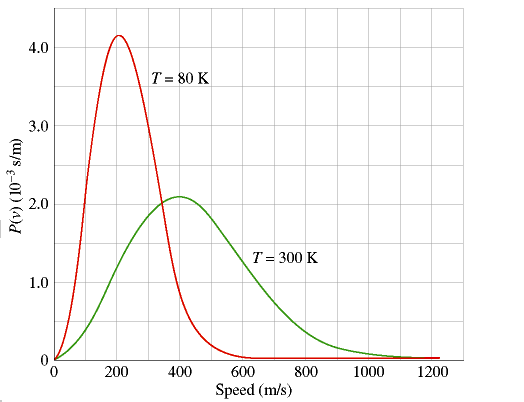
The graph shows the Maxwell-Boltzmann speed-probability curve for an ideal gas at two temperatures. The y-axis consists of the Probability present in more or less arbitrary units; and the x-axis consists of the speed of the molecule in m/s. This curve precisely connects the (instantaneous) speed of a gas molecule with the relative probability that it will have that speed. Prominent peaks are noticed on the curves, that correspond to the most probable speed of a molecule and to (approximately) the absolute temperature of the gas.
1) The Maxwell-Boltzmann curves significantly differ for a gas at 80 °K and at 300 °K. It should be noted that the peak becomes higher and very narrow, when gas get colder, the peak shifts to the left (lower temperature = slower molecules), however at low temperatures, the availability of energy is less, therefore the gas molecules show less collisions and move at speeds that don’t differ much from one another. In the limit where an ideal gas is taken to absolute zero, the molecules would stop moving altogether and therefore in fact be at constant speed.
2) the Maxwell-Boltzmann curves flatten out, at higher temperatures, the available energy is plenty, hence many more energetic collisions take place that potentially impel a molecule faster than the average speed. In particular, note the far right-hand region of both curves. At 1000 m/s, the probability of a T=80 molecule having that speed is essentially zero. But for T=300 the probability is only small, not zero. Therefore, even though the percentage of T=300 molecules moving at 1000 m/s is tiny by any standard, the ratio of the probabilities for the T=300 and T=80 gasses is quite large, because dividing by the T=80 case is almost like dividing by zero.
Calculation of most probable; average and root mean square velocities of molecules.
The distribution of velocities of gaseous particles remains constant although the velocity of gas particles keeps changing constantly. Hence, we cannot count on the individual velocity of each particle. and therefore, the particles average behaviour is taken into consideration. The particles that move in the opposite directions have velocities that have opposite signs. Since a gas’ particles are in random motion, it is possible that the particles will be moving in one direction and also the opposite direction, meaning that the average velocity for a collection of gas particles equals zero; this value is not helpful therefore the average velocity is determined using an alternative method.
By squaring the velocities and taking the square root, we overcome the “directional” component of velocity and simultaneously acquire the particles’ average velocity. Since the value excludes the particles’ direction, we now refer to the value as the average speed. The root-mean-square speed is the measure of the speed of particles in a gas, defined as the square root of the average velocity-squared of the molecules in a gas.
It is represented by the equation: vrms=√3RTMvrms=3RTM, where vrms is the root-mean-square of the velocity, Mm is the molar mass of the gas in kilograms per mole, R is the molar gas constant, and T is the temperature in Kelvin.
The root-mean-square speed takes into account both molecular weight and temperature, two factors that directly affect the kinetic energy of a material.
Real Gases
The term ‘real gas’ usually refers to a gas that does not behave like an ideal gas. Their behaviour can be explained by the interactions between the gaseous molecules. These intermolecular interactions between the gas particles are the reason why real gases do not adhere to the ideal gas law. Therefore, real gases can be defined as non-ideal gases whose molecules occupy a given amount of space and have the ability to interact with each other.
It is important to note that in most cases, the behaviour of a real gas is almost the same as that of an ideal gas. Therefore, in many applications, a detailed analysis of the deviation of real gases from ideal behaviour is unnecessary. Reasonably accurate calculations can be conducted by applying the ideal gas equation to these real gases. However, it is important to note that a gas must be considered as a real gas when it is approaching its condensation point. Furthermore, almost all gases must be considered as real gases as they approach their critical points. Other situations in which gases can be considered as real gases include situations in which the pressure applied to the gas is very high, and in order to explain the Joule-Thomson effect. It is also important to note that the deviation of a real gas from the behaviour of an ideal gas can be expressed in terms of the compressibility factor (also known as the gas deviation factor or the compression factor; usually denoted by the symbol ‘Z’).
Compressibility Factor
Compressibility factor also known as the gas deviation factor or the compression factor is a measure of deviations in the thermodynamic property of a real gas from an ideal gas behaviour. In simple words, we can say that it is a correction factor that best describes the amount of gas that deviates from its perfect behaviour at a certain temperature and pressure. Normally, it is used to modify the law of ideal gas.
Compressibility Factor is also often defined as “the ratio of molar volume of gas to that of an ideal gas.” It is expressed as Z = pV / RT.
Derivation from Ideality
Real gases do not obey ideal gas equation under all conditions. They nearly obey ideal gas equation at higher temperatures and very low pressures. However, they show deviations from ideality at low temperatures and high pressures.
The deviations from ideal gas behaviour can be illustrated as follows:
The isotherms obtained by plotting pressure, P against volume, V for real gases do not coincide with that of ideal gas, as shown below.
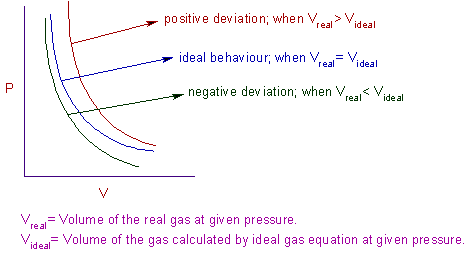
It is clear from above graphs that the volume of real gas is more than or less than expected in certain cases. The deviation from ideal gas behaviour can also be expressed by compressibility factor, Z.
The ratio of PV to nRT is known as compressibility factor.
(or)
The ratio of volume of real gas, Vreal to the ideal volume of that gas, Vperfect calculated by ideal gas equation is known as compressibility factor.
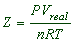
But from ideal gas equation:
PVperfect = nRT
or
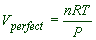
Therefore
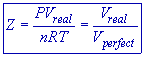
* For ideal or perfect gases, the compressibility factor, Z = 1.
* But for real gases, Z ≠1.
Van der Waals Equation of State for Real Gases – Derivation
Kinetic theory of ideal gases assumes the gaseous particles as –
In practice, Van der Waals assumed that, gaseous particles –
Volume Correction in Van der Waals Equation
As the particles have a definite volume, the volume available for their movement is not the entire container volume but less.
Volume in the ideal gas is hence an over-estimation and has to be reduced for real gases.
Volume of the real gas VR = Volume of the container/ideal gas (VI) – Correction factor(b)
VR = VI – b.
If the particles are independent, then,
Total volume of the particle = number of particle x volume of one particle =\left (n\frac {4}{3} \pi {{r}^ {3}} \right) =(n34πr3)
But the particles are not independent, they do interact. Van der Waals equation was derived by Johannes Diderik van der Waals in the year 1873. The equation is basically a modified version of the Ideal Gas Law which states that gases consist of point masses that undergo perfectly elastic collisions. However, this law fails to explain the behaviour of real gases. Therefore, Van der Waals equation was devised and it helps us define the physical state of a real gas.
More significantly, the Van der Waals equation takes into consideration the molecular size and molecular interaction forces (attractive and repulsive forces). Sometimes, it is also referred to as Van der Waals equation of state.
Emphasis on Van der Waals equation of state and its application to the calculation of Boyle's temperature
Van der Waals Equation for 1 mole gas is...
(P + a/V²) (V - b) = RT
or,
P = (RT/V - b) - a/V²
Hence
PV = {RTV/ (V - b)} - a/V
So
TB = [d(PV)/dP] T = [RT/ (V - b) - {RTV/ (V - b) ²} + a/V²] (dV/dP) T
= [{RT (V - b) - RTV/ (V - b) ²} + a/V²] (dV/dP) T
= [{- RTb/ (V - b) ²} + a/V²] (dV/dP) T
But when
T = TB, [d(PV)/dP] T = 0 and (dV/dP) T ≠ 0
So
RTBb/ (V - b) ² = a/V²
or,
TB = (a/Rb) {(V - b)/V} ² Since P → 0, V is large.
Thus...
(V - b)/V ≃ 1
Hence...TB = a/Rb
Qualitative treatment of the Structure of the Liquid State
The atoms in the Liquid state are not as strongly bound as the ones in solid state and not as loosely bound as the ones in the gaseous state. This gives them benefits of being in the intermediate stage. As the atoms can easily move, we have fluidity in the liquid state. It can also be easily stored as there are still pretty good bonds between the atoms. This structure also lets them form effective solutions where a solvent and a solute can mix together coherently to form a useful liquid. A liquid is made up of tiny vibrating particles of matter, such as atoms, held together by intermolecular bonds. Like a gas, a liquid is able to flow and take the shape of a container. Most liquids resist compression, although others can be compressed.
Various approaches to the structure of liquids
The unique behaviour of the "liquid state", put together its richness phenomena observations, renders the liquid very interesting to the scientific community. Most of the vital reactions takes place in the biological and chemical systems occurring in the liquid like environments. Liquids are also used widely in many industrial applications, it is for these many reasons, the understanding their properties at their molecular level is of uttermost importance.
The basic reason is that liquids lack long-range order and many particle interactions occur in the liquid state, that are introduced at liquid state theory and also to the existing stimulation techniques, numerous technical problems occur that need specific approaches. Also, many of the elementary processes that take place in liquids, including molecular translational, rotational and vibrational motions, structural relaxation, energy dissipation and especially chemical changes in reactive systems occur at different and/or extremely short timescales.
Liquids and solids that are amorphous possess a rich and varied array of short to medium range order that is obtained from related reactions and chemical bonding. The different structures however produce different physical properties and various applications.
The study of liquid is to understand the purpose so as to gain insight of their physical properties and their behaviour. Resulting in a better understanding and can be predicted and used in specific applications. As the structure and behaviour of liquids is a complex body problem, it has been too computationally intensive to solve using quantum mechanics directly. Instead, a variety of NMR, Molecular dynamics, diffraction and similar techniques are most commonly used.
Accurate determination of a liquid structure, especially at high temperatures, remains challenging, as reflected in the scatter between different measurements. The experimental challenge is compounded by the process of the numerical transformation from the structure factor to the radial distribution function. The resulting uncertainty is often greater than that required to resolve issues associated with changes in the short-range order of the liquid, such as the existence of liquid–liquid phase transitions or correlations between thermophysical properties and structure. In the present contribution it is demonstrated for liquid bismuth as a model system that the structure factor can be obtained to high accuracy, by comparing several independent measurements in different setups. A simple method is proposed for improving the accuracy of the radial distribution functions, based on the extension of the finite range of momentum transfer, q, in the measured data by analytical asymptotic expressions. A unified mathematical formalism for the asymptotic dependence of the structure factor is developed and the asymptotic form of the Percuss–Yevick hard-sphere solution is obtained as a special limiting case. The multiple expressions in the literature are shown to reflect uncertainty in the nature of the repulsive interatomic interaction at short separation distances. Applying this asymptotic method, it is shown that it enables access to details of the fine structure of the liquid and its temperature dependence.
Radial Distribution Function
To completely understand the liquid state of matter, first we need to understand its behaviour on the molecular level. Such kind of behaviour can be characterized by two quantities known as intermolecular pair potential function u, and the radial distribution function, g. The information regarding the energy due to the interaction of a pair of molecules is given by the pair potential and is a function of the distance r between their centres. However, the radial distribution function provides information on the structure or the distances between pairs of molecules. If g and u are known for a substance, macroscopic properties can be calculated.
For an ideal gas, the volume of the molecules is negligible as they are no forces between the molecules. —g is unity, which means that the chance of encountering a second molecule, when moving away from a central molecule is independent of position. However, in a solid, g shows distinct values at a distance that corresponds to the locations associated with the solid’s crystal structure.
The structure of a liquid is however an intermediate of the two extremes, they neither have completely ordered structure of a solid crystal nor the randomness of an ideal gas. The molecules in a liquid move about freely showing some disorder as they are relatively close to one another. Although numerous possible positions a molecule may assume with respect to another others are more likely to show different positions.
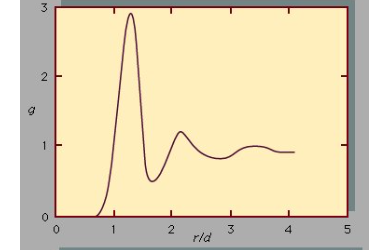
This is illustrated by Figure, which shows an example of the radial distribution function for the dense packing typical of liquids. In this figure, g is a measure of the probability of finding the centre of one molecule at a distance r from the centre of a second molecule. For values of r less than those of the molecular diameter, d, g goes to zero. The fact is that no two molecules can occupy the same space, the possible position of a second molecule with respect to a central molecule is a little more than a diameter away. which reflects the fact that in liquids the molecules are packed almost against one another. The second most likely location is a little more than two molecular diameters away, but beyond the third layer preferred locations damp out, and the chance of finding the centre of a molecule becomes independent of position. The pair potential function, u, is a large positive number for r less than d, assumes a minimum value at the most preferred location (this corresponds to the maximum of the curve in Figure, and damps out to zero as r approaches infinity. The large positive value of u corresponds to a strong repulsion, while the minimum corresponds to the net result of repulsive and attractive forces
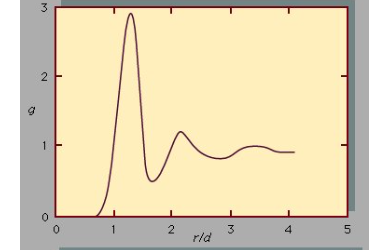
The radial distribution function, g is a measure of the probability of finding the centre of one molecule at a distance r from a central molecule, the molecular diameter is d
Physical properties of liquids
i) Molar volume: At standard Temperature and Pressure (STP) the molar volume (Vm) is the volume occupied by one mole of a chemical element or a chemical compound. It can be calculated by dividing the molar mass (M) by mass density (ρ). Molar gas volume is one mole of any gas at a specific temperature and pressure has a fixed volume.
Molar Volume Formula: The Molar volume is directly proportional to molar mass and inversely proportional to density. The formula of the molar volume is expressed as
Vm=Molar mass Density
Where Vm is the volume of the substance.
The standard temperature used is 273 Kelvin or 0oC,
Standard pressure is 1 atmosphere, i.e., 760 mm Hg.
Experimentally, one mole of any gas occupies a volume of 22.4 litres at STP. The equation can be expressed as
1 mole of gas at STP = 22.4 litres of gas.
ii) Vapour pressure:
Vapour pressure, is the pressure exerted by the vapour, when the vapour is in equilibrium with the solid or liquid state or with both that belong to the same substance. However, the conditions have to be such that the substance can exist in both or all the three phases. Vapour pressure is a measure of the tendency of a material to change into the gaseous or vapour state, and it increases with temperature. The temperature at which the vapour pressure at the surface of a liquid becomes equal to the pressure exerted by the surroundings is called the boiling point of the liquid.
iii) Surface Tension:
The property of the surface of a liquid that allows it to resist an external force, due to the cohesive nature of its molecules."
The cohesive forces between liquid molecules are responsible for the phenomenon known as surface tension, the cohesive forces between molecules in a liquid are shared with all neighbouring molecules.
Those on the surface have no neighbouring molecules above and, thus, exhibit stronger attractive forces upon their nearest neighbours on and below the surface. Surface tension could be defined as the property of the surface of a liquid that allows it to resist an external force, due to the cohesive nature of the water molecules other than mercury, water has the greatest surface tension of any liquid.
iv) Parachor:
It is an empirical constant for a liquid that relates the surface tension to the molecular volume and that may be used for a comparison of molecular volumes under conditions such that the liquids have the same surface tension and for determinations of partial structure of compounds by adding values obtained for constituent atoms and structural features. It is also called as molar parachor, molecular parachor
Parachor is a quantity defined according to the formula: P = γ1/4 M / d where γ is the surface tension, M is the molar mass, and d is the density. Parachor has a volume multiplier and is therefore extensible from components to mixtures. Parachor "has been used in solving various structural problems"
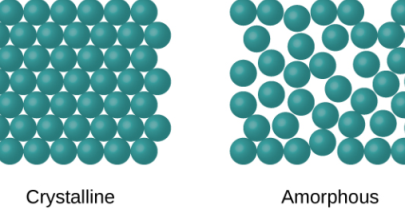
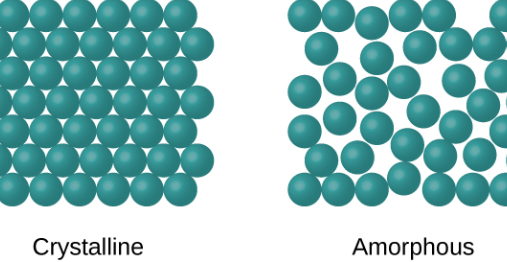
Types of solids
Examples of Crystalline solids include, sodium chloride, diamond and Quartz
Examples of amorphous solids are Rubber and Glass.
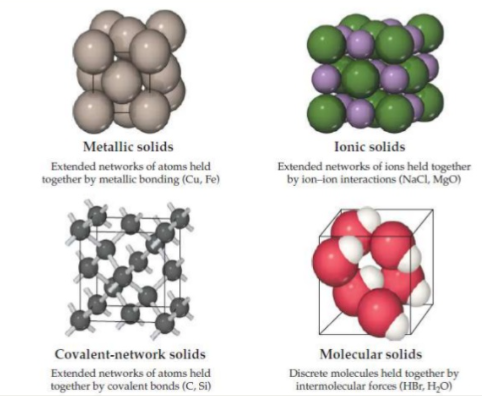
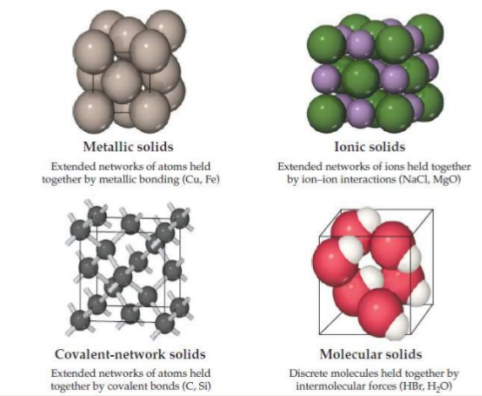
This form of bonding allows metals to conduct electricity.
Most of the metals are relatively strong without being brittle.
Difference between ionic and metallic bonding make the electrical and mechanical properties of ionic solids very different from those of metals.
This type of bonding can result in materials that are extremely hard like diamond and it is also responsible for the unique properties of semiconductors.
Crystal forces
A crystal is a body whose component atoms are arranged in a definite space lattices; and this arrangement is probably the result of the vectorial action of interatomic forces and, as a rule, finds outward expression in the development of flat crystal faces.
In general, crystals are rigid and show a high degree of homogeneity and are bounded by flat faces, but the fact that these characteristics re lacking in certain individual units has an important bearing in certain individual units has an important bearing on the theory of crystal growth and crystal forces.
In crystals there is a regular periodic arrangement in space of the component atoms. All theories of crystal structure are based on phenomena of diffraction and reflection of characteristic X-ray from oriented crystal plates. From this it may be inferred that the orderly arrangement of the atoms in interpenetrating space lattice is the result of the action of interatomic forces which are especially vectorial in character. However, little is known of the order of magnitude of these forces and of the law of their variation with distance.
Law of Constancy of angles
Law of constancy of interfacial angles:
This law states that angle between adjacent corresponding faces is inter facial angles of the crystal of a particular substance is always constant in spite of different shapes and sizes and mode of growth of crystal. This law is also known as Steno's Law.
The angle between the adjacent faces is called interfacial angle of the crystal of a particular substance. According to this law, it is of the same substance.
Inspite of different shapes and sizes and mode of growth of crystals, the interfacial angle is the same. The size and shape of the crystal formed depends on the conditions of crystallisation.
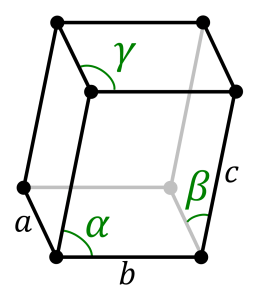
Seven Crystal systems
Crystal Systems
A Crystal System refers to one of the many classes of crystals, space groups, and lattices. In crystallography terms, lattice system and crystal, the system are associated with each other with a slight difference. Based on their point groups crystals and space groups are divided into seven crystal systems.
The Seven Crystal Systems is an approach for classification depending upon their lattice and atomic structure. The atomic lattice consists of a series of atoms that the appearance and physical properties of stone makes it possible to identify to which crystal they belong to. In a Cubic System crystal are said to represent the element earth. They are Seven Crystal Systems and are stated below with illustrated examples.
The Seven Crystal Systems
Triclinic System:
They are of the same length and all the three axes are inclined towards each other on the basis of the three inclined angles, the various forms of crystals are in paired forces. Some standard Triclinic Systems include Labradorite, Amazonite, Kyanite, Rhodonite, Aventurine Feldspar, and Turquoise.
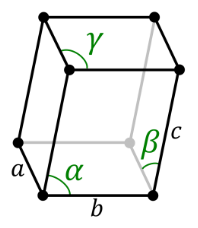
Triclinic System
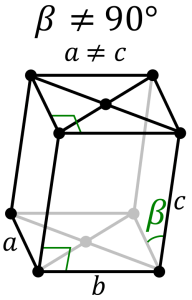
Monoclinic System:
It consists of three axes, where two are at right angles to each other and the third is inclined. All the three axes are of different lengths. Based on the inner structure the monoclinic system includes Basal pinacoids and prisms with inclined end faces. Some examples include Diopside, Petalite, Kunzite, Gypsum, Hiddenite, Howlite, Vivianite and more.
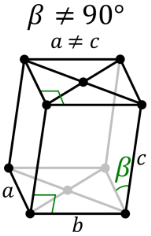
Monoclinic System
Orthorhombic System:
It consists of three axes that are at right angles to each other. The axes exist at different lengths. It is based on the rhombic structure includes various crystal shapes namely pyramids, double pyramids, rhombic pyramids, and pinacoids. Some common orthorhombic crystals include Topaz, Tanzanite, Iolite, Zoisite, Danburite and more.
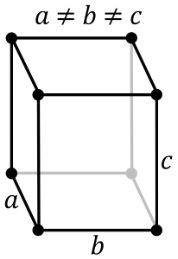
Orthorhombic System
Trigonal System:
The axis and angles in this system is same as in hexagonal systems. At the base of a hexagonal system (ross-section of a prism), there will be six sides. In the trigonal system (base cross-section) there will be three sides. Crystal shapes in a trigonal system include three-sided pyramids, Scalenohedral and Rhombohedra. Some typical examples include Ruby, Quartz, Calcite, Agate, Jasper, Tiger’s Eyes and more.
Trigonal/Pyramidal System
Hexagonal System:
The hexagonal system consists of four axes, of which three are of the same length and are present on one plane. The axes intersect each other at 60O angle. The fourth axis intersects with other axes at right angles. Crystal shapes of hexagonal systems include Double Pyramids, Double-Sided Pyramids, and Four-Sided Pyramids. Example: Beryl, Cancrinite, Apatite, Sugilite, etc.
Hexagonal System
Tetragonal Systems:
This system consists of three axes, where the main axes vary in length, which can be either long or short. The other two axes lie in the same plane and are of the same length. Based on the rectangular inner structure the shapes of crystal in tetragonal include double and eight-sided pyramids, four-sided prism, trapezohedrons, and pyrite.
Perovskite – Tetragonal Systems
Cubic System:
The system consists of three axes and are equal in length and intersect at right angles Crystal shapes of a cubic system based on inner structure (square) include octahedron, cube, and Hexacis coherdron. Example: Silver, Garnet, Gold, and Diamond.

Cubic System
Shapes of Seven Crystal laws.
Law of Rational indices
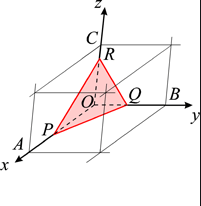
The law of rational indices states that the intercepts of any face of a crystal along the crystallographic axes are either equal to the unit intercepts (a, b, c) or some simple whole number multiples of them, e.g., na, n’a, n’’a etc are simple whole numbers
Let OX, OY and OZ represent the three crystallographic axes and let ABC be a unit plane. The unit intercepts will then be a, b and c. According to the above law, the intercepts of any face such as KLM, on the same three Axes will be simple whole number multiples of a, b and c respectively.
Hauy (1784,1801) was the person who deduced the law of rational indices, he made this law from the observations of the stacking laws that were required to build the natural faces of crystals by stacking up elementary blocks, for example cubes to construct the {110} faces of the rhomb-dodecahedron observed in garnets or the ½{210} faces of the pentagon-dodecahedron observed in pyrite, or rhombohedrons to construct the {21.1} (referred to an hexagonal lattice, {21¯0}{21¯0}, referred to a rhombohedral lattice) scalenohedron of calcite.
French mineralogist R.-J. Haüy (1743-1822) was responsible for showing the crystals forms could be reconstructed by suitable stacking laws of very small cleavage rhombohedra for calcite and cubes for garnets
Labelling the Planes
Look at the following figure:
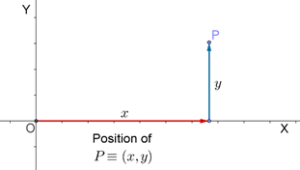
Thus, to label positions in a plane, we need exactly two real numbers.
The interesting point to be noted here is the position P will depend on how the number lines X and Y are chosen. Visually this is very obvious, however if we draw X and Y at different locations than the one shown above, then to reach the same position P from the new reference point you will have to travel different distances along X and parallel to Y.
Thus, the label assigned to each point depends on the position of the reference number lines X and Y in the plane.
Points to remember while labelling a plane
Miller indices
Miller indices were introduced in 1839 by the British mineralogist William Hallowes Miller, this method was also historically known as Millerian system and the indices as millerian.
The orientation of a surface or a crystal plane may be defined by considering how the plane (or any other parallel plane) intersects the main crystallographic axes of the solids, the application of a set of rules leads to the assignment of the miller indices (hkl); a set of numbers which quantify the intercepts and thus may be used to uniquely identify the plane or surface.to determine the crystallography planes we take a unit cell with three axes coordination system.
Rules of Miller indices
General principles
Qualitative idea of point and space groups
Point groups are (discrete) symmetry groups of Euclidean space which leave the origin fixed. Space has many symmetries, such as translations, which don't have any fixed point: everything gets moved. The point groups are those that keep a certain point fixed (we may choose that fixed point as the origin of the coordinate axes for notational convenience, but that's really immaterial).
Space groups are free of that restriction, and do include translations and glide reflections and other fancy stuff which has no fixed points.
The "discrete" part above refers to the fact that we are interested in collections of symmetries that are well-separated geometrically, as opposed to having infinitely many symmetries that are arbitrarily close to each other. For instance, the set of all rotations of the plane - by any arbitrary angle - is a group of symmetries, but it's not discrete: there are rotations that differ by an arbitrarily small angle.
Mathematicians (sometimes) and crystallographers (always) are interested in groups that are discrete, which for the most part can be taken to mean that their point part is finite and their translational part has some minimal translation amount. Physically this means that such groups partition space into solid chunks that get mapped to one another by those symmetries.
In the plane, a point group is either the set of rotations by multiples of a fixed angle of the form 2π/n2π/n for some integer nn, or the set of those symmetries plus reflections (the dihedral group). You should think of those as the set of symmetries of some regular polygon, with or without flips allowed.
Crystallographers tend to further restrict their attention to groups that preserve some lattice; of the planar point groups, only those with.
Elementary Idea of symmetry
In crystallography, Symmetry, forms the fundamental property of the orderly arrangements of atoms that are found in crystalline solids. Each atom arrangement found in the crystalline solid has a specific number of elements of symmetry, i.e., the atoms are not moved by changes in the orientation of arrangement of atoms.
One element is symmetry is Rotation, others include translation, reflection and Inversion. The elements of symmetry that are present in a particular crystalline solid determine its shape and physical properties.
Translations involves shift of crystals in a direction that replace each atom by item neighbouring atom so that the atoms look like they are unmoved.
Rotations help to turn the crystal around an axis of symmetry that passes through a crystal; the only rotations compatible with translational symmetry move the crystal through an angle of 360° divided by n, with n equal to 1, 2, 3, 4, or 6.
Reflections exchange the parts of the crystal on the two sides of a plane of symmetry (mirror plane) within the solid. Inversions move every atom to another position in the crystal; the old and new positions of the atom lie upon a line, at the middle of which is the centre of inversion. So-called improper rotations are rotations followed by reflections (known as roto reflections) or rotations followed by inversions (called roto inversions).
Symmetry of elements
A symmetry is a geometrical entity such as a line, a plane, or a point about which one can perform an operation of rotation reflection or inversion.
A symmetry operation is movement of a molecule or object about a symmetry element such that the resulting configuration is indistinguishable from the original.
A symmetry operation will transform a molecule into an equivalent or ideal configuration.
1.Identity E
2. Axis of symmetry [Cn]:
For e.g., water molecule
Principal and Subsidiary Axes:
3.Plane of Symmetry 

Classification of mirror plane:

4. Inversion centre of symmetry:
5. Improper axis of symmetry or rotation-reflection axis or alternate axis of symmetry:

Definition
Colloids (also known as colloidal solutions or colloidal systems) are mixtures of dispersed insoluble particles of one substance that are microscopic in nature, and are suspended in another substance. The size of these suspended particles in a colloid can vary from 1 to 1000 nanometres (10-9 metres). However, the condition remains that for a mixture to be termed as colloid, the suspended particles present in the mixture must not settle (in the manner that the particles of suspensions settle at the bottom of the container if left undisturbed). Solutions in colloidal state display Tyndall effect, wherein the beam of light incident on colloids are scattered due to the interactions between the colloidal particles and light.
The IUPAC definition of the colloidal state can be written as follows: “The colloidal state is the state of subdivision in which molecules or polymolecular particles having at least one dimension in the range of 1 nanometre and 1 micrometre, are dispersed in some medium “. Colloids usually feature substances that are evenly dispersed in another. Such mixtures where the substance is dispersed is called as the dispersed phase and the substance through which it is dispersed is called the continuous phase
In simple terms, colloids can be defined as, a mixture where one of the substances are split into minute particles that are we can define colloids as a mixture where one of the substances is split into very minute particles which are dispersed throughout a second substance. The minute particles are known as
colloidal particles.
Alternatively, we can also say that colloids are basically solutions in which solute particle size ranges from 1nm – 1000 nm. Colloids are heterogeneous in nature
Classification
Classification of Colloids
Colloids are classified into many types.
Classification Based on Physical State
(a) Solid Solution
In this dispersed phase solid and the dispersion medium. E.g.: gemstones.
(b) Aerosol
These colloids consist of air as the dispersion medium.
Example 1: Cloud. This contains air as dispersion medium and water drops as the dispersed phase.
Example 2: Dust. This contains air is dispersion medium and dent particle as the dispersed phase.
Example 3: Smoke. This contains carbon particles in the air.
(c) Gels
These contain solid dispersion medium and liquid dispersed phase
Example: Cheese, butter.
(d) Emulsion
These are liquid-liquid solutions in which the dispersed phase is liquid and liquid dispersed medium. Emulsion mainly consists of two aspects.
Oil in water type:
Oil is dispersed phase and water is dispersion medium
Example: Milk
Water in oil type:
Water is the dispersed phase and oil/fat is dispersion medium.
Example: Vanishing cream
Sols and gels are reversible and interconvertible. This is known as thixotropy.
Classification Based on Dispersion Medium
On the basis of dispersion medium sol are classified as;
(a) Hydrosol:
In these colloids water act as a dispersion medium.
Example: Starch
(b) Alcohol:
In this type, alcohol acts as a dispersion medium.
(c) Acrosol:
These contain a dispersed phase particle in the air.
Example: Smoke
Classification Based on Interaction Forces
On the basis of interaction forces between the dispersion medium and dispersed phase.
Lyophobic Sols: [Emulsoid]a) Surface Tension: It is same as that of the medium.
b) Viscosity: It is the same as that of the medium.
c) Irreversible: These are irreversible colloids when once dispersion medium is evaporated and again when the solvent is added no new sol is formed.
d) Stability: There is weak interaction between the dispersed phase and dispersion medium hence lyophobic sols are unstable.
e) Visibility: Particle can be detected using ultramicroscope.
f) Migration: Particle migrates either colloid an anode depending upon the charge of sol particle.
g) Action of electrolyte: When the electrolyte is added to sol, coagulation takes place.
h) Hydration: No hydration of sol takes place.
i) Examples: Metallic sols like Ag, gold etc
Lyophilic SolsThese are stable strong sols. A strong interaction is present between the dispersed phase and the dispersion medium. Following are the characteristics of lyophilic sols.
a) Surface tension: Lower than that of the medium.
b) Viscosity: Higher than medium.
c) Reversibility: These are reversible sols. When dispersion medium is evaporated and the solvent is added again the same type of sol is formed.
d) Stability: More stable due to strong interaction between the dispersed phase and the dispersion medium.
e) Visibility: The particles are visible under an electron microscope.
f) Addition of electrolyte: Small amount of electrolyte is required for the formation of sol.
g) Hydration: Extensive hydration takes place.
h) Example: gum, gelatin, starch
Preparation of colloidal solution
Stable colloids are also known as lyophilic sols, in these strong forces of interaction exist between the dispersed phase and the dispersion medium. These are prepared by the following suitable methods.
Condensation Method
In this method, small solute particles are condensed to form a dispersed phase particle.
1. Chemical methods:
a) By oxidation:
Colloidal sulphur can be obtained by passing oxygen gas through a solution of hydrogen sulphides. In this method any oxidising agent like HNO3, H3Br2 can also be used.
2H2S + O2 → 2H2O + 2S (Sulphur sol)
b) By double decomposition:
A solution of arsenic sulphide is obtained in this method. In this process hydrogen sulphide is passed through Arsenious oxide cold solution in water.
AS2O3 + 3H2S → AS2S3 + 3H2O Arsenic sulphide (sol)
c) By reduction:
A number of metals such as gold, silver, and platinum are obtained in a colloidal state by reacting the aqueous solution of these salts with suitable reducing agents such as formaldehyde, phenylhydrazine, hydrogen peroxide, stannous chloride etc.
2AuCl3 + 3SnCl2 → 3SnCl4 + 2Au (gold sol)
2AuCl3 + 3HCHO + 3H2O → 2Au + 3HCOOH + 6HCl
The gold sol prepared in the reduction of gold chloride solution has a purple colour and is called purple of Cassius.
d) By hydrolysis:
Many salt solutions are rapidly hydrolysed by boiling a dilute solution of their salts. For example, ferric hydroxide and aluminium hydroxide sols are obtained by boiling solutions of the corresponding chloride.
FeCl3 + 3H2O → Fe (OH)3 + 3HCl colloidal sol
Silicic acid sol is obtained by the hydrolysis by sodium silicate.
e) By double decomposition:
A sol of arsenic sulphide is obtained in this method. In this process hydrogen sulphide is passed through Arsenious oxide cold solution in water.
As2O3 + 3H2S → As2 S3 + 3H2O Arsenic sulphide (sol)
f) By excessive cooling:
A colloidal sol of ice is obtained in this process. Ice is taken in an organic solvent like chloroform ether. Sol of ice is obtained by freezing a solution of water in the solvent. The molecules of water are no longer in the solution separately combine to form particles of colloidal size.
h) By exchange of solvent:
In this process, colloidal sol of certain substances such as sulphur, phosphorus which are soluble in alcohol but insoluble in water can be prepared by pouring their alcoholic solution into water. For enough alcoholic solution of sulphur on pouring into water gives a milky colloidal solution of sulphur.
i) By change of physical state:
Sols of substance like mercury and sulphur are prepared by passing the vapour through cold water containing a suitable stabilizer such as ammonium salt or citrate.
Dispersion Methods
In these methods, large particles of a substance (suspension) are broken into smaller particles. The following methods are employed.
a) Mechanical dispersion
In this method, the substance is first grounded to coarse particles. It is then mixed with dispersion medium to get a suspension. The suspension is then grinded in a colloidal mill.
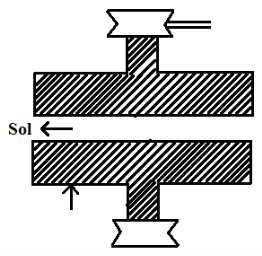
It consists of two metallic dyes nearly touching each other and rotating in the opposite direction at a very high speed 7000 revolution per minute. The space between the dyes of the mill is so adjusted that coarse suspension to great shearing force giving rise to particles of colloidal size. Colloidal solution of black ink, paints varnishes dyes are obtained by this method.
b) Bredig’s Arc Method or by Electrical Dispersion
This method is used to prepare sols of platinum, silver copper or gold. The metal whose sol is to be prepared is made as two-electrode which immersed in a dispersion medium such as water etc.

The dispersion medium is kept cool by ice. An electric arc is placed between the electrodes. The tremendous heat generated by and give colloidal solute. Electrolytes are used for this process for stabilization and cooling.
c) Peptization
The process of converting a freshly prepared precipitate into a colloidal solution is known as peptization. In this method as the electrolyte in smaller amounts is added which is known as peptization agent or peptizing agent. Cause of peptization is the adsorption of the ions of the electrolyte by the particles of the precipitate. Important peptizing agent are sugar gem gelatin and electrolyte.
Examples
1. Freshly prepared ferric hydroxide can be converted into the colloidal state by shaking it with water contains Fe3+ or OH– ions i.e., FeCl3 or NH4OH respectively.
Fe (OH)3 + FeCl3 → (Fe (OH)1 Fe) +3 + 3Cl– precipitate electrolyte
2. A stable sol of stannic oxide is obtained by adding a small amount of dilute HCl to stannic oxide precipitate similarly a colloidal solution of Al (OH)3 and AgCl are obtained by treating the corresponding freshly prepared with a very dilute solution of HCl and AgNO3 or KCl respectively.
Colloids contain ionic impurities and other categories of impure substances that decrease the quality of colloids used in various applications. Following are the methods to purify the colloids.
1) Dialysis
Method of separation of ionic substances from the colloidal solution by means of effusion through a suitable membrane is dialysis. The principle is that sol particle cannot pay through parchment paper or semipermeable membrane due to the impurity slowly diffused out of the base leaving pure colloid.
Precautions:
The distilled water in the container where a bag is immersed should be changed frequently to prevent the accumulation of crystalloids otherwise there is a possible change of diffusing back of impurities into the bag.

2) Electro Dialysis
Dialysis is a slow process and takes so much time for the removal of impurities. The process is improvised by an applied electrical force. This is known as electrodialysis. In this method two electrical plates are inserted into the distilled water and are connected to the terminals of source, long moves to the opposite electric plate with greater speed and the sol is purified.
3) Ultrafiltration
Normal filter papers cannot be used to filter the impurities of colloid since due to the large size of pores, impurities along with sol particle will be filtered off. The pore size is reduced by impregnating the papers in collodion solution which is 4 – s. Calculate nitrate solution in alcohol – ether mixture and dried with acetaldehyde. This is known as ultrafiltration and such papers are known as ultrafilter papers.
Properties of Colloids
Properties of colloids and the variation they show are a known fact sine the primitive age. Coagulation of milk that results in the formation of curd proves its familiarity.
Physical properties of colloids
(1) Dispersed medium (2) Dispersed phase
2. The known fact that colloidal dispersions do not have a detailed description. Yet their fragments are not detected by the human eye, due to the microscopic sizes of the particles in the solution.
3. In the colloidal dispersion, their colour is determined by the size of the particles in the solution. If the size of the particle is large the wavelengths of light that is absorbed will be longer.
4. As a result of its size, the colloidal fragments can easily be passed through a traditional filter paper. However, these particles can be filtered by using membranes such as animal, cellophane, and ultrafilters.
Electrical properties of colloids
Electrical double layer theory: In this theory, charge is imparted to the particles by placing ions which are adsorbed preferentially at immovable points which for the first layer. The second layer consists of diffused mobile ions. The charge present on both the layers is equal. This two-layer arrangement leads to a development of potential called zeta or Electrokinetic potential. As a result of this potential developed across the particles, under the influence of electric field these particles move.
Electrophoresis: in this system an electric field is employed to the colloidal solution, which helps in the movement of colloidal solution Depending upon the accumulation near the electrodes the charge of the particles can be predicted. The charge of the particles is positive if the particles get collected near a negative electrode and vice versa.
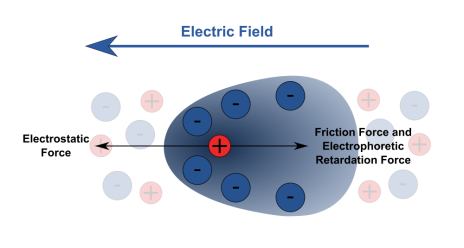
Electro-osmosis: It is a process in which the dispersing medium of the colloidal solution is brought under the influence of electric field and the particles are arrested.
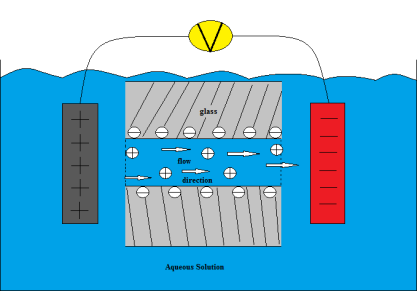
Optical properties of colloids
Light is scattered by the colloidal particles which defines the Tyndall effect, the light is absorbed by the colloidal particles. Once this light is absorbed a part of the light gets scattered in all directions the result of scattering exhibits this effect.
Kinetic properties of colloids
During the observation of the colloidal dispersion under an ultra-microscope, it is clearly seen that the particles are in a continuous movement in the solution. This random zigzag movement of the particles in the colloidal solution is called Brownian effect. This movement is mainly due to the unique bombardment of the molecules present in the dispersed medium on the colloidal particles.
Protection of colloids
Lyophobic sols such as those of metals like gold, silver etc. can be easily precipitated by the addition of a small amount of electrolytes.
They can be prevented from coagulation by the previous addition of some stable lyophilic colloids like gelatin, albumin, etc. This is because when a lyophilic sol is added to the lyophobic sol, the lyophilic particles form a layer around the lyophobic particles and this protect them from electrolytes.
If a small amount of gelatin is added to gold sol, it is not readily precipitated by the addition of sodium chloride. This process of protecting the lyophobic colloidal sol is called protecting colloid.
Gold number: The different protecting colloids differ in their protecting powers.
The minimum amount of the protective colloid in milligrams required to just prevent the coagulation of a 10 mL of a given sol when 1 mL of a 10% solution of sodium chloride is added to it. The coagulation of gold sol is indicated by change in colour from red to blue. Smaller the value of the gold number, greater will be protecting power of the protective colloid.
Application of Colloids
Colloids are widely useful in industries, medical and domestic applications.
As food items: Syrup, Halwa, Soup belongs to a colloidal type of system.
Medicine: Colloidal silver in the name of Argyrols, it acts as antiseptic for eye infection.
In Purification of air by Cottrell precipitator:
This process involves coagulation of solution particle. Dust or smoke is passed through the inlet of an electrified chamber which has a central electrical plate which is provided with opposite charge of a dent a smoke particle when dust passes the particles are coagulated and pure air is passed through another outlet.
Tanning of leather:
Animal skins are very soft, when these are immersed in the solution of tannin which has the opposite charge of animal skin, particles are coagulated and the skin becomes hard this is known as tanning of leather.
Formation of delta:
It involves coagulation of clay particles of the river with an electrolyte of seawater.
Key take away
The states of matter are divided into gases, solids, liquids and colloids.
Various gases do not always obey the gas laws in all conditions. Solids are amorphous and crystalline. The different structure of liquids, Colloids (also known as colloidal solutions or colloidal systems) are mixtures of dispersed insoluble particles of one substance that are microscopic in nature, and are suspended in another substance
References: