Unit – 3

Changes

3.1 Chemical Kinetics: Rate of reaction, order and molecularity, expression for specific rate constant of first order reaction, half life period, unit, experimental determination of order or reaction.

Chemical kinetics is an important concept in Physical Chemistry and deals with the various aspects that occur in a chemical reaction, the term Kinetics deals with the rate of change of some quantity. For example, acceleration is the rate of change of velocity and also the rate of displacement is given by Velocity.

Usually, based on this rate, chemical reactions can be classified as fast (e.g.: Na + H2O), Moderate (Mg + H2O) and slow (esterification) reactions.

Chemical kinetics also called reaction kinetics helps to understand the rates of reactions and how they are influenced by certain conditions. It further helps to summarize and analyse the information regarding the mechanism of a particular reaction and also define the characteristics of a chemical reaction.

Rate of a Reaction

The rate of reaction refers to the speed at which the products are formed from the reactants in a chemical reaction. It provides information about the time required in which a reaction can be completed. For example, the reaction rate of the combustion of cellulose in fire is very high and the reaction is completed in less than a second.

The rate of a reaction can be defined as the speed at which the reactants are converted to products, when we consider the chemical reactions, the rate at which these reactions occur differs to a large extent. Some chemical reactions are nearly instantaneous, while others usually take some time to reach the final equilibrium.

As per the general definition, the speed with which a reaction takes place is referred to as the rate of a reaction.

For example, wood combustion has a high reaction rate since the process is fast and rusting of iron has a low reaction rate as the process is slow.

Factors Affecting the Rate of Reaction

The various factions that can affect the rate of a chemical reaction are:

Nature of the reaction

Effect of concentration on reaction rate

Pressure factor

Effect of temperature on the reaction rate

Order and Molecularity

Molecularity of the reaction can be defined as the total number of reacting species in a rate-determining step. On the other hand, the order of reaction is the summation of powers of concentration of the reactant molecules in the rate equation of the reaction.

The molecularity of a reaction signifies the number of molecules, number of atoms, or ions that interact with each other for a chemical reaction to take place within the time limits.

 The main differences between order and order of reaction are given below.

Expression for Specific rate constant of first order reaction

A first-order reaction is a chemical reaction, where the rate of the reaction is solely dependent on the concentration of only one reactant. Generally, in such reactions, if the concentration of the reactant of the first order is doubled the rate of the reaction is also doubled. Similarly, if the first-order reactant concentration is increased five-fold, it will be accompanied by a 500% increase in the reaction rate.

A first-order reaction can be defined as a chemical reaction in which the reaction rate is linearly dependent on the concentration of only one reactant. In other words, a first-order reaction is a chemical reaction in which the rate varies based on the changes in the concentration of only one of the reactants. Thus, the order of the reaction is equal to 1.

Examples of First-Order Reactions

Differential Rate Law for a First-Order Reaction

A differential rate law can be employed to describe a chemical reaction at a molecular level. The differential rate expression for a first-order reaction can be written as:

Rate = -d[A]/dt = k[A]1 = k[A]

Where,

Integrated Rate Law for a First-Order Reaction

Integrated rate expressions can be used to experimentally calculate the value of the rate constant of a reaction. In order to obtain the integral form of the rate expression for a first-order reaction, the differential rate law for the first-order reaction must be rearranged as follows.

This expression is the integrated form of the first-order rate law.

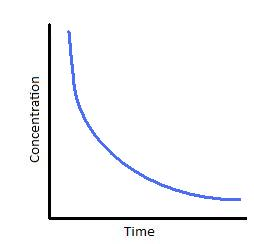
Graphical Representation of a First-Order Reaction

The concentration v/s time graph for a first-order reaction is provided below.

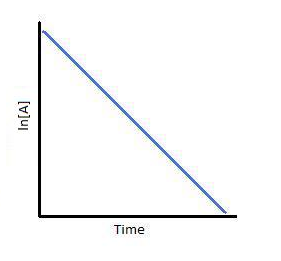
For first-order reactions, the equation ln [A] = -kt + ln[A]0 is similar to that of a straight line (y = mx + c) with slope -k. This line can be graphically plotted as follows.

Thus, the graph for ln[A] v/s t for a first-order reaction is a straight line with slope -k.

Half-Life of a First-Order Reaction

The Half – life of a chemical reaction. (denoted by ‘t1/2’) is the time taken for the initial concentration of the reactant(s) to reach half of its original value. Therefore,

At t = t1/2, [A] = [A]0/2

Where [A] denotes the concentration of the reactant and [A]0 denotes the initial concentration of the reactant.

Substituting the value of A = [A]0/2 and t = t1/2 in the equation [A] = [A]0 e-kt:

  [A]0/2  = [A]0 e-kt1/2:--- ½ = e -kt1/2

 Taking the natural logarithm of both sides of the equation in order to eliminate ‘e’ the following equation is obtained.

ln(1/2 ) = -kt1/2 ---/ t1/2 = 0.693/k

Thus the half-life of first order reaction is equal to 0.693/k where k denotes the rate constant. 

UNITS

k is the first-order rate constant, which has units of 1/s.

The method of determining the order of a reaction is known as the method of initial rates.

The overall order of a reaction is the sum of all the exponents of the concentration terms in the rate equation.

Experimental determination of order or reaction

To experimentally determine the rate of a reaction, the concentrations of the reactants and the products needs to be measured throughout the chemical reaction. If the order of the reaction is known, the data can be plotted and the integrated laws can be applied.

 For example, if the reaction is first-order, a plot of ln[A] versus t will yield a straight line with a slope of –k.

There are two main ways to measure the concentrations of reactions:  changes in the physical property can be observed and measured or the reaction samples are taken and their concentrations are measured directly.

Physical Measurements

Physical measurements are performed while the reaction is taking place. These measurements however have the advantage of not disturbing the reaction system and can be carried out or measure quickly. For example, if the total number of moles of gas changes during a gas reaction, in the course of the reaction, the changes in pressure can be measured by keeping the volume as constant., the other physical measurements include optical methods like measuring the changes in light polarization, changes in refractive index of the solution, or the common feature of change in the colour of the solution that brings about the spectrum. Common electrical methods are the changes in the conductivity of a solution, mass spectroscopy and electric potential in a cell. Other methods include thermal conductivity, viscosity, heats of reaction, and freezing points.

Chemical Measurements

The concentration of the reactant is measured in the chemical measurements, a minimum amount of the sample is taken during the reaction process, the reaction is halted by adding another reactant or by diluting or cooling the mixture to stop the reaction. A major disadvantage of this process is that by adding another reagent or by or removing a part of the reaction system gradually brings about changes over time, another important thing to be noted is that there is a time lag between when the sample is taken and the reactant is measured, this makes the measurement less accurate.

Using Beer’s Law to Measure Concentration Over Time

One oxidized form of buckminsterfullerene (C60) is C60O3. When a solution of C60O3 is warmed, the compounded decomposes, releasing O2 and creating C60O. The reaction is given by:

C60O3                    O2+C60O

The rate of this reaction can be monitored by measuring the absorbance of the solution. The absorbance is given by Beer’s law:

[latex]A=abC[/latex]

In this equation, a is the absorptivity of a given molecules in solution, which is a constant that is dependent upon the physical properties of the molecule in question, b is the path length that travels through the solution, and C is the concentration of the solution. Determination of C is our main concern.

The data is plotted, by passing the solution of the reactant of interest using a spectrometer and the absorbance of the solution is measured with time.

Oxidized buckminsterfullerene absorbance

As we know the absorbance of a solution is proportional to the concertation of the solution, the concentration of C60O3 in solution will be proportional to absorbance. By observing the absorbance as a function of time, it becomes important to observe the concentration also as function of time.

By Beer’s law, the absorbance of the solution is directly proportional to the concentration of the C60O3 in solution, by observing the absorbance as a function of time, it becomes important to observe the concentration also as function of time.

In this case, the rate law is given by:

[latex]rate=k [C_ {60}O_3] [/latex]

Therefore, a plot of the rate versus the absorbance will yield a straight line with a slope of k.

Reaction rate vs. absorbance

The absorbance is directly proportional to the concentration, so this is simply a plot of the rate law, rate = k[C60O3], and the slope of the line is the rate constant, k.

 3.2 Dilute Solutions and Changes of State-I: Colligative properties, Osmosis, Osmotic pressure and its experimental determination, van't Hoff factor, vapour pressure, Roult's Law of lowering of vapour pressure.

Colligative properties

Colligative properties, is a property of a solution that depends on the ratio between the total number of solute particles present in the solution and the total number of solvent particles. The Colligative properties are not dependent on the chemical nature of the solution’s components. Thus, these properties are linked to several quantities that express the concentration of a solution., such as molarity, normality, and molality. The four colligative properties that can be exhibited by a solution are:

The word “colligative” is taken from the Latin word has been adapted or taken from the Latin word “colligatus” which means to “bound together”. When a solution is defined, the colligative properties help to analyse how the properties of solution is linked to the concentration of solute in a solution.

What are Colligative Properties?

Non-volatile solute that are dilute exhibit some properties that depend only on the number of solute particles present in the solution and not on the solute present in the solution. These properties are called colligative properties. Such properties are seen mostly in dilute solutions.

We can further consider colligative properties as those properties that are obtained by the dissolution of a non-volatile solute in a volatile solvent. Generally, the solvent properties are changed by the solute where its particles remove some of the solvent molecules in the liquid phase. This also results in the reduction of the concentration of the solvent.

Meanwhile, when we talk about the given solute-solvent mass ratio, colligative properties are said to be inversely proportional to the solute molar mass.

Colligative Properties Examples

We can observe the colligative properties of solutions by going through the following examples. If we add a pinch of salt to a glass full of water its freezing temperature is lowered considerably than the normal temperature. Alternatively, its boiling temperature is also increased and the solution will have a lower vapour pressure. There are changes in its osmotic pressure as well.

Similarly, if we add alcohol to water, the solution’s freezing point goes down below the normal temperature that is observed for either pure water or alcohol.

Osmosis

Osmosis Definition

“Osmosis is a process by which the molecules of a solvent pass from a solution of low concentration to a solution of high concentration through a semi-permeable membrane.”

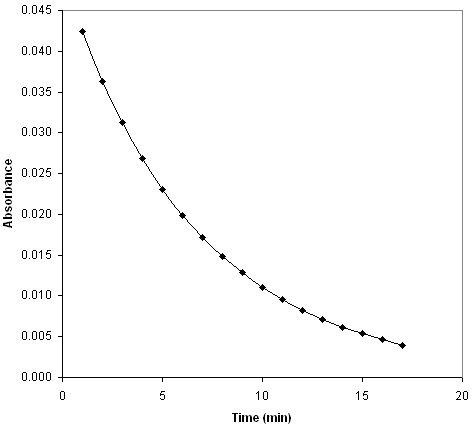
Fig: Osmosis through a semipermeable membrane

Osmosis is a process that is passive in nature and does not require any energy, in the process the molecules move from a region of higher concertation to a region of lower concentration until the concentration are the same eon both sides of the semipermeable membrane. Any solvent can undergo the process of osmosis including gases and supercritical liquids.

Osmotic Solutions

There are three different types of solutions:

An isotonic solution is a solution where the concentration of the solutes is the same both inside and outside the cell.

A hypertonic solution is a solution where the concentration of the solute is higher outside the cell than inside the cell.

A hypotonic solution the concentration of the solute is higher inside the cell than the outside.

Types of Osmosis

Osmosis is of two types:

Effect of Osmosis on Cells

Osmosis affects the cells differently. An animal cell will lyse when placed in a hypotonic solution compared to a plant cell. The plant cell has thick walls and requires more water. The cells will not burst when placed in a hypotonic solution. In fact, a hypotonic solution is ideal for a plant cell.

An animal cell survives only in an isotonic solution. In an isotonic solution, the plant cells are no longer turgid and the leaves of the plant droop.

The osmotic flow can be stopped or reversed, also called reverse osmosis, by exerting an external pressure to the sides of the solute. The minimum pressure required to stop the solvent transfer is called the osmotic pressure.

Significance of Osmosis

Osmotic Pressure

It is the pressure that is required to prevent water from diffusing through a membrane by osmosis. Osmotic pressure is estimated by the concentration of the solute. Water diffuses to the area of higher concentration from the area of lower concentration, this continues until the concertation is uniform throughout (when concentrations of the substances in both areas are different)

Osmotic pressure can be calculated using the equation:

Π=MRT

where Π denotes the osmotic pressure,

M is the molar concentration of the solute,

R is the gas constant,

T is the temperature

Determination of Osmotic Pressure by Pfeffer’s method

Abbe Nollet (1748) was the first person to notice the phenomenon of osmosis and made measurements of the osmotic pressure. He chose pigs bladder as the semi permeable membrane, however the membrane failed to meet the requirements as the results were semi quantitative and the pig’s bladder was not a very good semi-permeable membrane. It was the botanist Pfeffer, he was successful in making a good semi permeable membrane and succeeded in making measurements for osmotic pressure. The Pfeffer Cell Apparatus, invented by Wilhelm Pfeffer in 1877, the instrument measured the minimum pressure that was required to stop a pure solvent from passing into a solution across a semipermeable membrane that is called the osmotic pressure.

The osmotic pressure of a solution at a particular temperature is defined as the additional hydrostatic pressure that is required that builds up when the solution is separated from the solvent by a semipermeable membrane. It is denoted by p.

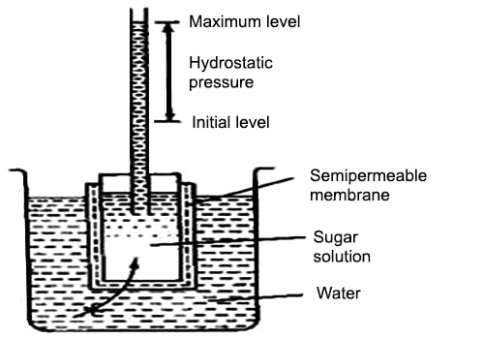
Fig: The Pfeffer’s apparatus for determination of osmotic pressure

Pfeffer’s method: He developed a technique by depositing gelatinous copper ferrocyanide in the pores of an earthen pot, this earthen pot was used as the semipermeable membrane. Osmosis is mainly a diffusion of a solution through a semipermeable membrane. His apparatus for the measurement of osmotic pressure is shown in Figure. The porous pot, that has deposits of copper ferrocyanide in its pores is connected to a manometer. The pot s filled with the solution to be examined and this is placed in a vessel that consists of the solvent. The entire set up is paled in a thermostat and maintained this way till equilibrium is reached. At equilibrium, the difference in the heights of mercury columns in the two tubes gave the osmotic pressure. Osmotic pressure is the excess pressure that should be applied to a given solution in order to increase its vapor pressure until it becomes equal to that of the solution. The osmotic pressure of a solution is the pressure difference needed to stop the flow of solvent across a semipermeable membrane.

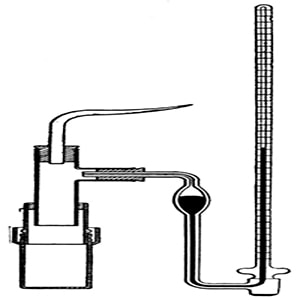
Fig: Pfeffer‘s apparatus for measurement of osmotic pressure

The osmotic pressure of a particular solution is proportional to the molar concentration of the solute particles present in the solution. This method is slow as it may take few days for equilibrium to be reached, also if the pressure is too high the membrane may break and it cannot be used again. When a semipermeable membrane (animal bladders, skins of fruits and vegetables) separates a solution from a solvent, then only solvent molecules are competent to pass through the membrane. Pfeffer’s method was improved by Berkeley and Hartley.

Van't Hoff factor

The Van’t Hoff factor offers insight on the effect of solutes on the colligative properties of solutions. It is denoted by the symbol ‘i’. The Van’t Hoff factor is defined as the ratio of the particle’s concentration formed when a substance is dissolved to the substance concentration by mass.

The degree to which a substance dissociates or associates in a solution is described by the Van’t Hoff factor. For example, the value of i is generally 1 when the non-electrolytic substance is dissolved in water, however when an ionic compound is dissolved in water the value of i is equal to the total number of ions present in one formula unit of the substance.

For example, the Van’t Hoff factor of CaCl2 is ideally 3, as CaCl2 dissociated into one Ca2+ ion and two Cl– ions. Sometimes these ions associate with each other causing a decrease in the total number of particles in the solution.

This factor is named after the Dutch physical chemist Jacobus Henricus Van’t Hoff, who won the first Nobel Prize in chemistry. It is important to note that the measured value of the Van’t Hoff factor for electrolytic solutions is generally lower than the predicted value (due to the pairing of ions). The greater the charge on the ions, the greater the deviation.

Van’t Hoff explained that when solutes are dissolved in a solvent they dissociate into ions. Since colligative properties depend only on the number of solute particles, the dissociation of solute molecules into ions results in an increase in the number of particles and hence affects the colligative properties.

Effects of Association/Dissociation

The effects of the association or dissociation of a solute on the solution, its colligative properties, and the Van’t Hoff factor are tabulated below.

Vapour Pressure

Vapour pressure is a property of liquid which related to evaporation. In other words, it is the pressure that is exerted by a vapour in equilibrium with its phases either as solid or liquid at a given temperature and in a closed system.

In simple terms, we can define vapour pressure as a measure of the tendency of a material to change its state to solid/liquid to gas or vapour when the temperature increases. It indicates the rate of evaporation of liquid. It is also closely related to the tendency of particles to escape from the liquid or solid-state.

Relation Between Vapour Pressure and Temperature

The substance with a high vapour pressure at room temperature is called a volatile substance. The temperature at which the vapour pressure at the surface of a liquid is equal to the pressure exerted by surrounding is denoted as the boiling point of that substance.

As the temperature of a liquid substance increases, the molecules’ kinetic energy also increases. Thus, the number of molecules transitioning into a vapour also increases and thereby increasing the vapour pressure of the liquid.

Simply say, with an increase in the temperature, the vapour pressure becomes sufficient to overcome atmospheric pressure and lift the liquid to form vapour bubbles inside the bulk of a substance. Volatile components such as gases and solvents are characterised by high vapour pressure can be transported with winds and components with low vapour pressure are transported with soil, sediment etc.

Fig: Pictorial Representation of Concept of Vapour Pressure

The vapour pressure of any substance increases nonlinearly with temperature. As moving to height, atmospheric pressure decreases because air is less dense at higher altitude. Because the atmospheric pressure is low then the vapour pressure of liquid needs to be lower to reach the boiling point. Therefore, low heat is required to make vapour pressure equal to atmospheric pressure.

The concept of vapour pressure can be understood by this example, when a closed container is taken and half filled with water. The container is then heated and evaporation takes place, the water in the container escapes in the form of vapour, some of the molecules will be converted to vapour during evaporation. As a result, the amount of liquid in the container decreases and the amount of vapour increases. The evaporated gas molecules will randomly move along the empty space in the container, as a result of this random movement, some of the molecules will come in contact with the uppermost layer of the container and begin to condense.

In the beginning the rate of evaporation will not be equal to the rate of condensation, after sometime this equilibrium will be reached. At that equilibrium, the rate of evaporation is equal to the rate of condensation.

As time changes the number of molecules in a gaseous state increases while the rate of condensation also increases. At last, it reaches a stage where the rate of evaporation becomes equal to the rate of condensation. This stage is known as the equilibrium stage. At this point, the pressure exerted by the molecules on the wall is known as the vapour pressure of the liquid.

Water Vapour Pressure

When we talk about the vapour pressure of water, it is nothing but the pressure that the water vapour experiences when it is in thermodynamic equilibrium. It will be in its condensed state. Generally, when the pressure is high water condenses.

Vapour Pressure Units

Vapour pressure can only be calculated in a closed container. Vapour pressure is usually measured in standard units of pressure. The SI unit is the pascal (Pa) where one pascal is equal to one newton per square meter (N·m−2 or kg·m−1·s−2).

Factors Affecting Vapour Pressure

There are four factors on which vapour pressure depends. They are:

Nature Of Liquid

Nature of liquid is explained on the basis of its intermolecular forces. That is, as the magnitude of the intermolecular forces increases vapour pressure will decrease.

Effect Of Temperature

As the temperature of the liquid increases the kinetic energy associated with the liquid also increases. And due to this increase in kinetic energy the escaping tendency of molecule increases and hence vapour pressure increases. So, we can conclude that vapour pressure is directly proportional to temperature.

Concentration Of Solute

The presence of solute in the liquid will decrease the vapour pressure. And this fall in vapour pressure also varies with the concentration of solute.

Vapour Pressure Is Independent Of

Humidity

Temperature is the only property that affects the vapour pressure for a certain amount of water vapour in the air. Humidity will affect only if all the other variables are constant. So don’t be confused between the effect of temperature and humidity.

Volume

Vapour pressure will not be affected by the volume of the container. As we know that liquid in the container will be in equilibrium with the vapour. When the volume is changed say decreased, then some of the vapour in the container turns into a liquid state. And if the volume increases some of the liquid will change into its vapour state.

Surface Area

Normally vapour pressure is independent of surface area. Change in surface area will not affect the vapour pressure of a substance.

Roult's Law of lowering of vapour pressure

Raoult’s law has been named after François-Marie Raoult, a French chemist who while conducting an experiment found out that when substances were mixed in a solution, the vapour pressure of the solution decreased simultaneously. Raoult’s law was established in the year 1887 and is also considered as the law of thermodynamics.

Raoult’s law states that a solvent’s partial vapour pressure in a solution (or mixture) is equal or identical to the vapour pressure of the pure solvent multiplied by its mole fraction in the solution.

Mathematically, Raoult’s law equation is written as;

Psolution = ΧsolventP0solvent

Where,

Psolution = vapour pressure of the solution

Χsolvent = mole fraction of the solvent

P0solvent = vapour pressure of the pure solvent

Relative Lowering of vapour pressure

The ratio of the lowering of vapour pressure of a solution and the vapour pressure of the pure component is known as relative lowering of vapour pressure.

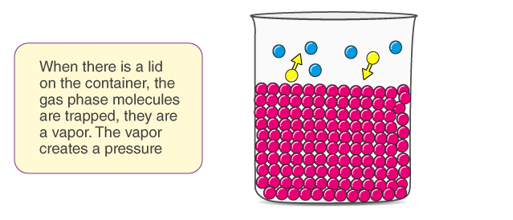
The vapour pressure of a liquid is the pressure applied by its gaseous phase where condensation and vaporization are in equilibrium, when a non-volatile substance is dissolved in a volatile liquid it results in lowering of the liquid’s vapour pressure.

This concept can be explained by understanding the effect of non-volatile solute molecules on the liquid’s tendency of vaporisation., for vaporisation to take place the solvent molecules must be present at the surface of the solution, the rate of vaporisation is reduced by the presence of non-volatile solutes, as they decrease the surface area available to the solute molecules.

The net result is that the vaporisation condensation equilibrium is achieved with fewer solvent molecules in the vapour phase, the presence of non-volatile solutes lowers the vapour pressure of a solution by impeding the evaporation of solvent molecules.

Raoult’s law describes the relationship between the vapour pressures of solution components and the concentrations of the components.

The partial pressure exerted by any component of an ideal solution is equal to the vapour of the pure component multiplied by its mole fraction in the solution.

If A is the solvent and B is solute we can write

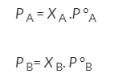
PA  is the partial pressure exerte by component A in the solution , POA  is the vapour pressure of Pure A and XA is the mole fraction in the solution.

B is a non volatile substance in one whose vapour pressure is negligible containing only non volatile solutes is due only to the solvent.

Since the solvent is the only volatile component of this solution, its vapour pressure may be computed as per Raoult’s law.

Since PB is zero

3.3 Experimental determination of relative lowering of vapour pressure and molecular weight determination, relation between osmotic pressure and lowering of vapour pressure

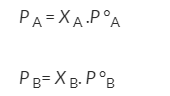
Experimental determination of relative lowering of vapour pressure and molecular weight determination

Relative lowering of vapour pressure (ΔP)

The vapour pressure of a non-volatile, non-electrolyte solution is always lower than the vapour pressure of the pure solvent. When a closed system is considered in which a pure solvent is in equilibrium with the vapour, the Molar Gibbs free energy of solvent in the liquid and gaseous state are (ΔG = 0) at equilibrium. When a solute is added to a solvent dissociation takes place and free energy(G) decreases due to increase in entropy. For equilibrium to be maintained the free energy of the vapour phase must also decrease. At a given temperature, the only way to lower the free energy of the vapour is to reduce its pressure. Thus, the vapour pressure of the solution must decrease to maintain the equilibrium.

We know that from the Raoult's law the relative lowering of the vapour pressure is equal to the mole fraction of the solute

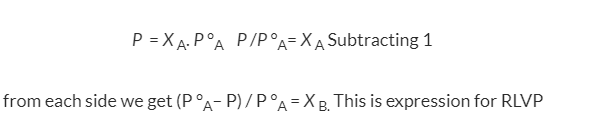
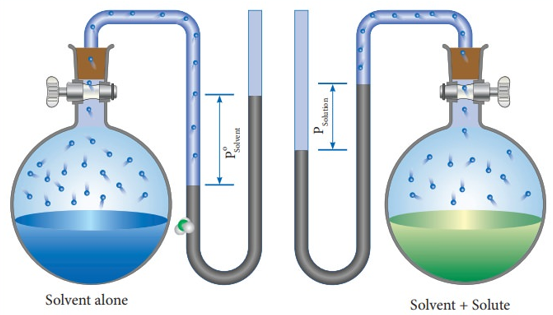
Fig: Measuring relative lowering of vapour pressure

From the above diagram, it is clear that the relative lowering of vapour pressure depends only on the mole fraction of the solute (xB) and is independent of its nature. Therefore, relative lowering of vapour pressure is a colligative property.

Determination of molar mass weights from relative lowering of vapour pressure

The molar mass of a non-volatile solute can be determined by measuring the relative lowering of vapour pressure, for this a known mass of the solute is dissolved in a known solvent. The relative lowering of vapour pressure is measured experimentally.

According to Raoult’s law the relative lowering of vapor pressure is,

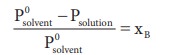
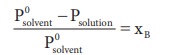
Let wAand wB be the weights of the solvent and solute respectively and their corresponding molar masses are MA and MB, then the mole fraction of the solute xB is

Here, nA & nB are the moles of the solvent and the solute respectively. For dilute solutions nA>>nB. Hence nA +nB ≈ nA. Now

Number of moles of solvent and the solute are,

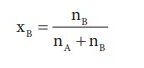
Thus

From the equation the molar mass of the solute (MB) can be calculated using the known the values of wA, wB, MA and the measured relative lowering of vapour pressure.

Relation between osmotic pressure and lowering of vapour pressure

Van’t Hoff equation for dilute solutions is

π=Vn​RT......(i)

In case of a dilute solution. The volume of solution can be taken as equal to that of the solvent. If N is the number of moles of the solvent of molecular weight M and density ρ, the volume V is given by

V = NM/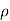  ----------------------(ii)

Or n/N = π M/ 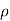RT --------------------(iii)

From Raoult’s law 
 

P o – P / P o = n/N

P o – P / P o = πM/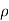RT

P o – P  = πM/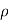RT  x P o

The factor M/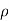RT  x P o  is constant temperature

P o – P  α π

Or lowering of V.P α osmotic pressure.

3.4 Dilute Solutions and Changes of States-II: Elevation of boiling point of solution, depression of freezing point of solutions, experimental determination of colligative properties, abnormal colligative properties of solutions

Elevation of boiling point of solution

If a non-volatile solute is added resulting in the lowering of vapour pressure through Raoul’s law, then the temperature must be raised to restore the vapour pressure to a value that corresponds to the pure solvent. The temperature at which vapour pressure is 1 atm will be higher than the normal boiling point by a known specific amount called the boiling point elevation. If addition of a non-volatile solute lowers the vapor pressure of the solution via Raoult's law, then it follows that the temperature must be raised to restore the vapor pressure to the value corresponding to the pure solvent. In particular, the temperature at which the vapor pressure is 1 atm will be higher than the normal boiling point by an amount known as the boiling point elevation. the precise relationship between the boiling point of the solution and the solvent molar fraction is very complicated, but for dilute solutions the elevation of the boiling point is directly proportional to the molal concentration of the solute:

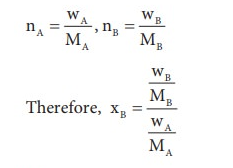
Bear in mind that the proportionality constant KB is a property of the solvent because this is the only component that contributes to the vapor pressure in the model we are considering in this section.

The boiling point of a liquid is the temperature at which the vapour pressure is equal to atmospheric pressure. The addition of non-volatile liquid to a pure solvent, there is a decrease in the vapour pressure of the solution, to make this vapour pressure equal to atmospheric pressure, the temperature of the solution has to be increased. The difference in the boiling point of the solution and the boiling point of the pure solvent is termed as elevation in boiling point.

If T0b is the boiling point of the pure solvent and Tb is the boiling point of the solution then elevation in boiling point is given as

∆Tb =T0b-Tb

Experimental results show that there is a relation between elevation in boiling point and molality ‘m’ of the solute present in solution

∆Tb ∝ m

∆Tb = kb m

Where,

kb = molal elevation constant

Substituting the value of ‘m’ in the above relation we get

∆Tb = 1000 x kb x m2 / M2 x m1

Where,

m2 = mass of solvent in g

M1 = mass of solvent in kg

M2 = molar mass of solute

Freezing Point Depression

The freezing point of a substance is the temperature at which the solid and liquid forms can coexist indefinitely meaning they are in equilibrium that is, they are in equilibrium. In the presence of these conditions the molecules pass between the two phases at an equal rate, as their escaping tendencies from the two phases are similar.

 For example, a liquid solvent and its solid like water and ice are at equilibrium given in ( below), on addition of non-volatile solute (such as salt, sugar, or automotive antifreeze liquid) to the water. This will have the effect of reducing the mole fraction of H2O molecules in the liquid phase, and thus reduce the tendency of these molecules to escape from it, not only into the vapor phase (as we saw above), but also into the solid (ice) phase. This will have no effect on the rate at which H2O molecules escape from the ice into the water phase, so the system will no longer be in equilibrium and the ice will begin to melt.

If the solid is prevented from melting the tendency of the molecules to escape, from the solid should be reduced, and this can be only achieved by reducing the temperature., this helps to lower the tendency of molecules to escape from both the phases but it affects those in the solid more than those in the liquid, so we eventually reach the new, lower freezing point where the two quantities are again in exact balance and both phases can coexist .

If vapour pressure is taken into consideration, then the vapour pressure of the solid and liquid should have the same freezing point. Dilution of the liquid (the solvent) by the non-volatile solute results in the decrease of vapour pressure of the solvent by the Raoult’s law, therefore reducing the temperature of the vapour pressure of the liquid frozen forms of the solution will be equal. As with boiling point elevation, in dilute solutions there is a simple linear relation between the freezing point depression and the molality of the solute:

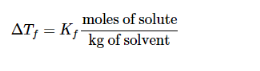
Note that Kf values are all negative!

The freezing point of a substance is defined as the temperature at which the vapour pressure of its liquid is equal to the vapour of the corresponding solid. According to Raoult’s law when a non-volatile solid is added to the solvent its vapour pressure decreases and now it would become equal to that of solid solvent at a lower temperature. The difference between the freezing point of the pure solvent and its solution is called depression in freezing point.

If T0f is the boiling point of the pure solvent and Tf is the boiling point of the solution then depression in freezing point is given as

∆Tf =T0f-Tf

Just like elevation in boiling point, depression in freezing point is also directly related to molality ‘m’.

∆Tf = 1000 x kf x m2 / M2 x m1

Where,

k f = molal depression constant

m2 = mass of solvent in g

M1 = mass of solvent in kg

M2 = molar mass of solute

Experimental determination of Colligative Properties

Measurement of Elevation of Boiling Point

The elevation of boiling point in a dilute solution is small and requires a very sensitive thermometer, the Beckmann thermometer is specifically used for this purpose.

Beckmann thermometer: Beckmann thermometer is a differential thermometer. The thermometer is designed in such a way that it records very minute changes temperature, but does not measure the actual temperature of the solvent or of the solution. The thermometer has several designs the most common one is described below.

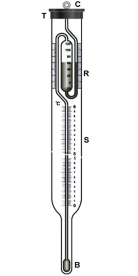
Figure: Beckmann thermometer

The thermometer consists of a large bulb B present at the bottom and a reservoir with mercury R present at the top, the thermometer is calibrated from 0to 6K and the wale S is subdivided into 0.01 K. the mercury in the two reservoirs can be accustomed by careful manipulation, depending on whether ebullioscopy or cryoscopy measurements are carried out.

Beckmann’s Method: this apparatus is generally used for estimating the elevation of temperature. A known volume of a given mass of the solvent is first taken into the boiling tube to fill about two-thirds of its capacity.

By definition the boiling point is the temperature at which the liquid vapour pressure is equal to the surrounding pressure and also the liquid turns into vapour. The boiling tube is connected to a reflux condenser on one side and a small tube on the other side E for the addition of solute. An insulated jacket surrounds the boiling tube and the Beckman thermometer is inserted into the boiling tube through a rubber stopper, such that the lower bulb of the thermometer touches the solvent, The boiling point of a liquid is the temperature at which its vapour pressure is equal to the pressure of its surrounding environment.

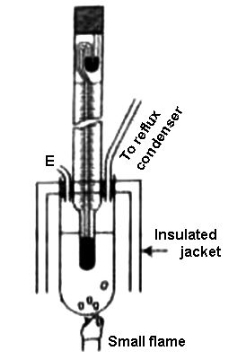
Figure: Complete Beckmann apparatus

The boiling tube is heated with the help of a Bunsen burner or an electric supply, initially the thermometer reading is noted which shows the boiling point of the pure solvent is recorded. The experiment is repeated after adding the solute of known mass. The difference in Beckmann’s reading in these two experiments gives a measure of the elevation of the boiling point. Since the mass of the solute, solvent, and K for the solvent are known, the relative molar mass of the solute can easily be determined. When a non-volatile solute is added to a solvent, the vapor pressure of the resulting solution is lower than that of the pure solvent.

Elevation in boiling point: We know that pure water boils at 100 °C at 1 atm pressure, but the boiling point changes when a small amount of salt is added. Therefore, when solute is added, the vapour pressure of the solvent decreases, this occurs due to the displacement of the solvent molecules by the solute It has been experimentally proven that adding any form of non-volatile solute to a liquid increases its boiling point. The lower number of solvent molecules at the surface means that fewer will evaporate, and thus the vapor pressure is lowered. The amount by which the boiling point changes are directly proportional to the amount of solute added. For the vapor pressure to equal the atmospheric pressure, a higher temperature is required, and a higher boiling point is observed.

Freezing Point Depression

When a small amount of non-volatile solute is dissolved in a volatile solvent, the vapor pressure of the solvent over the solution will be less than the vapor pressure of the pure solvent at the same temperature. Therefore, the temperature at which the equilibrium vapor pressure reaches atmospheric pressure is higher for the solution than for the pure solvent. Similarly, because of the reduction in vapor pressure over the solution the freezing point of the solution, is lower than the freezing point of pure solvent. The amount by which the freezing point of the solution is decreased from that of the pure liquid, is called the freezing point depression. The solute in this is laboratory experiment is naphthalene, C10H8

 which has the following structure and is non polar. The freezing point will be the temperature where the graph plateaus since the kinetic

energy doesn’t change during the physical state change. For a solution

on, the graph will look a little different. Instead of a long horizontal portion, the graph will start gradually curving downward shortly after levelling off. This occurs because as the solution freezes,

the part of the solution that hasn’t frozen yet will

 become more concentrated since the solute remains in the solution.

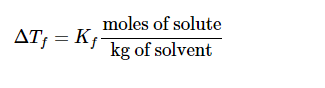
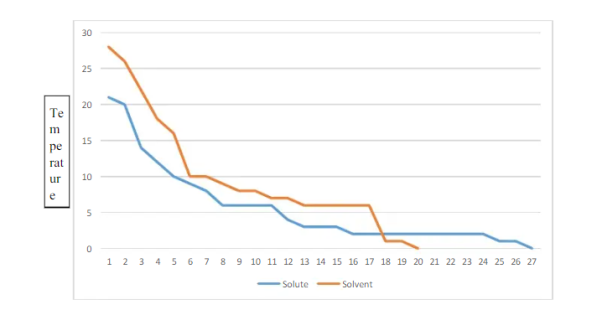
Figure. Plot of Temperature Vs Time

When a dilute solution begins to freeze, the solid crystals of solvent form at a lower temperature than they do when the pure liquid solvent is cooled. This phenomenon is called freezing point depression and is a colligative property that depends only on the concentration, and not the chemical properties, of the solute.

The quantitative expression of freezing point depression is:

ΔTf = Kf m, where m is the molality (moles solute per kg

of solvent), Kf is the freezing point depression constant of the solvent

and ΔTf is the difference between the freezing point of the pure solvent and that of the solution. The constant Kf depends on the solvent but not on the solute. The solvent will becyclohexane, which has

Kf = 20. This method is clearly inadequate for opaque mixtures, and it is subject to errors from a phenomenon known as super cooling. A more accurate technique is to measure a cooling curve, which is a temperature vs. time plot for a sample losing heat at an approximately constant rate.

Abnormal Colligative Properties of solutions.

The colligative properties are dependent on the number of particles of the solute, in few cases when the solute dissociates or associates in the solution, abnormal results occur for molecular mass

As studied earlier the colligative properties of a solution depends solely on the number of particles of the solute and not on their nature. But sometimes while measuring colligative properties abnormal results are obtained due to the following reasons:

Van’t Hoff Factor

In order to account for extent of association or dissociation, Van’t Hoff introduced a factor 'i'.

Degree of Association

Degree of association is defined as the fraction of the total number of molecules which associate to form a bigger molecule.

Degree of Dissociation

Degree of dissociation is defined as the fraction of the total number of particles that dissociate, i.e., break into simpler ions.

3.5 Processes at Solid Surface: Elementary idea of crystal growths, Adsorption: Physisorption and chemisorption, chemisorbed species. Idea of catalytic activity at surfaces, anti-catalytic processes such as hydrogenation, oxidation, cracking and reforming.

Elementary Idea of Crystal growths

A crystal is a solid substance, where the atoms, ions and molecules are organised in an orderly pattern that repeats itself and extends in all three spatial dimensions. The Crystal growth is an important stage of the crystallization process and involves addition of new atoms, polymer strings and ions into the characteristic arrangement of the crystalline lattice. The typical growth follows an initial stage of either heterogeneous or homogeneous nucleation. unless a "seed" crystal, purposely added to start the growth, was already present.

The action of the crystal produces a crystalline solid, where the atoms and molecules are closely packed, that have fixed positions in space relative to each other. The properties of the crystalline states of matter features a distinct structural rigidity and very high resistance to deformation. Most crystalline solids exhibit high values of both young’s modulus and shear modulus of elasticity. However, liquids and fluids exhibit low shear modules and typically display the capacity for macroscopic viscous flow.

The science of crystal growth is aimed to understand how and by what mechanism crystals nucleate and grow, and their forms, perfections, homogeneities and textures are determined. Interesting enough, the science of crystal growth has its root in the same 17th Century as structural crystallography started. For crystal growth and morphology of inorganic matter of simple system, it has now reached to a level that relevant phenomena are understandable in terms of atomistic process. Interests have now expanded to the problem of forms and textures exhibited such as by organic and inorganic crystals formed in living organs through living activities, namely to the problems involved in far more complicated and complex systems. Efforts are now-being paid to build a bridge between living and non-living worlds, through understandings of growth and forms of crystals

Adsorption: Physisorption and chemisorption

Adsorption:  It is basically the process of accumulation of molecular species at the surface instead of solid or liquid bulks.

Adsorption is usually a surface phenomenon and the best example that we can relate to is the air becoming dry in the presence of silica gel. During this, the molecules of water get adsorbed on the surface of the gel. In essence, during adsorption, the molecules or atoms or ions of a gas or a liquid get attached to the surface.

Depending on the substance being deposited and adsorbed, adsorption is classified into two types:

Physisorption

The process is exothermic in nature and is also called physical adsorption. The adsorption enthalpy is relatively low about 20 to 40 kJ/mol. Weak forces such as Van der Waals forces are responsible for accumulation of gas on the solid surfaces

Physisorption lacks specificity because of the adsorbent (the surface or the material on which the process of adsorption takes place) in the given surface does not show any particular gas. It has reversible nature that is physisorption of gas by a solid can be reversed to a solid by gas.

Gas + solid = Solid/Gas + Heat

An example of physisorption is the adsorption of gases like hydrogen, nitrogen etc at lower temperature on the surface of adsorbent like charcoal.

Physisorption is dependent on the surface area of the adsorbent, with the increase in surface area the adsorption also increases. For example, finely divided metals and porous substances have a large surface area. So that they are considered as good adsorbents. It also depends on the nature of the adsorbate (the accumulation of molecular species or substance at the surface).

Chemisorption

Chemisorption is also known as chemical adsorption. In chemisorption, adsorption takes place in adsorbed substance that is held by chemical bonds. Chemisorption has high specificity that is it is highly specific, and it takes place only if there is a chemical bonding between adsorbent and adsorbate.

Chemisorption is a process that favours high pressure and is irreversible in nature, due to chemical bonding enthalpy of adsorption which is nearly 80 to 240 kJ/mol. Physisorption of gas adsorbed at a lower temperature may be converted into chemisorption at a higher temperature.

Chemisorption depends on the surface area. As the surface area of the adsorbent increases, chemisorption also increases. An example of chemisorption is the adsorption of hydrogen, nitrogen etc on the surface of adsorbent like ferrous catalyst at a high temperature.

Difference Between Physisorption and Chemisorption

Chemisorbed Species

Chemisorbed species are formed during a reaction on the surface of the catalyst, this forms one of the established facts on catalysis. Some species may be simple like hydrogen atoms, while some are novel and have no corresponding role in ordinary chemical compounds. Some species show no participation in the reaction. The knowledge of what species are formed for a given system in catalytic mechanisms is yet to be discovered.

This remarkable improvement in catalytic performance could be primarily attributed to the enhanced Ag–Co3O4 metal–support interaction induced by the formation of uniform, dispersive, and suitable size metallic Ag nanoparticles. The activation, activity, consumption–regeneration, identification, and reaction of surface-adsorbed oxygen along with the activity of bulk lattice oxygen were characterized by various designed and in situ techniques. The results demonstrated that the chemisorbed superoxide species (O2–) play the potentially responsible role for boosting soot combustion, while the bulk lattice oxygen is much less active within the tested temperatures, inducing a negligible activity contribution. Moreover, soot-temperature programmed reduction, isothermal kinetic study, and density functional theory calculation provided supplementary support for the enhancement effect of Ag–Co3O4 combination in the activation and utilization of surface-adsorbed oxygen. The overall objective of this work is to identify the role of surface-adsorbed oxygen and bulk lattice oxygen for soot oxidation over Ag/Co3O4 catalysts

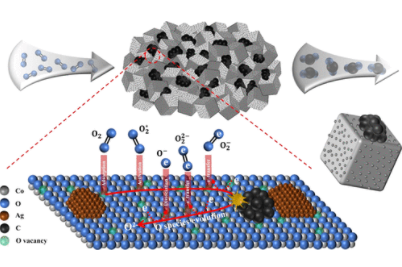
Fig:  Ag–Co3O4 metal–support interaction

Chemisorbent materials, based on porous amino silicas, are among the most promising adsorbents for direct air capture applications, one of the key technologies to mitigate carbon emissions.

Idea of catalytic activity at surfaces

Catalysis is the process of increasing the rate of a chemical reaction. by adding a substance known as a catalyst. Catalysts are not consumed in the catalysed reaction but can act repeatedly. Often only very small amounts of catalyst are required.

Catalytic oxidation reactions require specific oxidant, either from O2 or other oxygen-containing oxidant, to accomplish the oxidation reactions in which the oxidants are chemically adsorbed and activated on active sites at catalyst surfaces. Activation of oxygen at the active sites that have unsaturated coordination structures, therefore, plays a key role to lower operation temperature in many catalytic oxidation reactions; however, the competitive adsorption of reactants blocks the chemisorption of oxygen and, hence, prohibits the activation of oxygen at the active sites. In this case, higher operation temperature is required to activate oxygen in these catalytic reactions. Activation of lattice oxygen at the surface of catalysts would provide an alternative to enhance the catalytic activity in oxidation reactions. The dynamic equilibrium of defect reaction between oxygen vacancy and adsorbed oxygen at the surface of catalyst would deliver a continuous supply of activated lattice oxygen for the oxidation reactions, leading to the reduction of the operation temperatures.

Isolated sites with impurity ions are one of the ideal states of supported metal catalyst, which can uniformly distribute the metal ions on the surface of substrates. Isolated active sites are the centre of catalytic activity in many heterogeneous reactions and would deliver high activity and high selectivity and provide a new solution to study the catalytic mechanisms. Three-way catalysis plays a key role in automotive catalysis in which lowering the operation temperature would be essential to minimize exhaust emissions. Currently preferred Pt-loaded oxide catalysts operate at a relatively high temperature of ∼150 °C to maintain the complete oxidation of CO with air. The strong chemisorption of CO molecules at the surface of Pt catalysts blocks the activation of oxygen, thus leading to the high operation temperatures in catalytic reactions. The activation of lattice oxygen linked to the active sites would be an alternative method to reduce operation temperature, but it remains a fundamental challenge to induce complete CO oxidation at lower temperatures.

Porous single crystals combining both single-crystalline properties and interconnected pores would deliver a unique advantage to create well-defined structures at the twisted surfaces that are kinetically trapped. The large surface areas in the porous architectures would sufficiently host chemical reactions. The surface with clear top-layer atoms is therefore confined by the long-range ordering of lattice structures in the porous single-crystalline (PSC) architectures. The activation of lattice oxygen at the surface could be further manipulated through a surface engineering strategy such as element doping in the lattice. The well-defined surface structures thus provide an advantage for the construction and identification of active sites, which is expected to tailor the chemical interactions with adsorbed species through engineering the electronic structures at the surfaces. Here, the porous single crystals at centimetre scale are typical PSC monolithic catalysts. Traditional monolithic catalysts in polycrystalline states are mainly prepared from catalyst particles by mechanical forming and sintering. In contrast, PSC monoliths are in single-crystalline states with three-dimensional porous microstructures. They combine the advantages of the long-range ordering of lattice structures and the disordering of interconnected pores in a single-crystalline porous architecture. Therefore, they could deliver higher stability like bulk single crystals and higher activity like nanocrystals in catalysis.

Transition-metal oxides such as manganese oxides (MnOx) are commonly used as catalyst substrates, which show various morphologies and phases, multiple 3d electron configurations, and broad ranges of oxygen storage capacities in catalytic oxidation reactions. The oxygen vacancies at the surface of MnOx are the main surface defects, and they can normally interact with metal species to construct the active sites or interfaces. In catalytic reactions, the dynamic equilibrium of oxygen nonstoichiometric simultaneously arises from the reversible defect reactions between the oxygen vacancy and adsorbed oxygen at surfaces, thus providing a unique opportunity to activate lattice oxygen at surfaces. The manipulation of active sites and their electronic structures at the well-defined surfaces would lead to controllable chemical interactions between the active sites and adsorbed species during the catalytic oxidation of CO with air.

Anti-Catalytic processes

Hydrogenation

Hydrogenation is a reduction reaction that involves the addition of hydrogen (usually as H2). In case any organic compounds are hydrogenated they become more "saturated" with hydrogen atoms. The process usually involves the need for the use of a catalyst, as hydrogenation occur spontaneously at high temperatures. The most common catalysts are nickel, platinum, or palladium.

Hydrogenation is known to reduce the number of double bonds and triple bonds in hydrocarbons, while dehydrogenation removes hydrogen atoms and increases the number of double and triple bonds.

Hydrogenation has many applications, but most people are familiar with the reaction as the one used to make liquid oils into semi-solid and solid fats. There may be some health concerns associated with hydrogenation of unsaturated dietary fats to produce saturated fats and trans fats

Oxidation

Oxidation is a process that involves the loss of electrons that occur in a reaction by an atom, ion or molecule is increased. The reverse occurs in reduction, that occurs when the electrons are gained or the oxidation state of an atom, molecule, or ion decreases.

An example of a reaction is that between hydrogen and fluorine gas to form Hydrofluoric acid:

H2 + F2 → 2 HF

In this reaction, hydrogen is being oxidized and fluorine is being reduced. The reaction may be better understood if it is written in terms of two half-reactions.

H2 → 2 H+ + 2 e-

F2 + 2 e- → 2 F-

Note there is no oxygen anywhere in this reaction

Cracking

Cracking is a process where complex organic molecules like long chain hydrocarbons or kerogens are broken into smaller molecules called light hydrocarbons, the rate of the catalyst used depends much on factors like the temperature and presence of catalyst.

Types of Cracking

Cracking is a chemical process which is used in oil refining. To produce by-products such as cooking oil, ethanol, liquefied petroleum gas, diesel fuel, jet fuel and other petroleum distillates, cracking removes large hydrocarbon molecules in raw crude oil.

Cracking is a term used for splitting of large clusters of hydrocarbons into small and more functional pieces. This is achieved by using high temperature and pressure with or without the presence of the catalyst or at lower temperature and pressure. Cracking is the most important process for the commercial production of gasoline and diesel fuel.

Reforming

Reforming, is a process where the hydrocarbon is rearranged to alter its properties, the process is applied frequently to low-quality gasoline stocks to improve the characteristics of combustion.

 Thermal Reforming: the properties of low-grade naphtha’s are altered, by exposing molecules that exhibit high octane numbers, to high temperatures and pressure. 

Catalytic reforming: the process uses a catalyst mainly platinum, to yield a similar result. Mixed with hydrogen, naphtha is heated and passed over pellets of catalyst in a series of reactors, under high pressure, producing high-octane gasoline.

Applications of reforming

Aromatic hydrocarbons have octane numbers higher than 100, while the straight-run gasoline has the octane number of 55.

The straight-run gasoline (octane number 55) is first distilled to obtain a fraction containing n-hexane, cyclohexane and methyl cyclopentane. This fraction is then heated with a platinum catalyst to convert the cyclohexanes into benzene and toluene (octane number > 100).

Key takeaway

The reaction rate depends on the concentrations of the reactants, the temperature of the reaction, the phase and surface area of the reactants, the solvent, and the presence or the absence of a catalyst.  It seeks to develop mathematical equations that describe and predict the course of chemical reactions in terms of the species involved in the reaction.

Colligative properties, is a property of a solution that depends on the ratio between the total number of solute particles present in the solution and the total number of solvent particles. The Colligative properties are not dependent on the chemical nature of the solution’s components 

References: