Unit – 4
Production
Laws of returns to scale refers to the long-run analysis of the laws of production. In the long run output can be increased by varying all factors. Thus, in this section we study the change in output as a result of change in all factors. In other words, we study the behaviour of output in response to change in the scale. When all factors are increased in the same proportion an increase in scale occurs.
Scale refers to quantity of all factors which re employed in optimal combinations for specified outputs. The terms ‘returns to scale’ refers to the degree by which output changes as a result of a given change in the quantity of all inputs used in production. We have three types of returns to scale: constant, increasing and decreasing. If output increases by the same proportion s the increases more than proportionally with the increase in inputs, we have increasing returns to scale. If output increases less than proportionally with the increases in inputs we have decreasing returns to scale. Thus, returns to scale may be constant, increasing or decreasing depending upon whether output increases in the same, greater or lower rate in response to a proportionate increase in all inputs. Returns to scale can be expressed as a movement along the scale line or expansion path which we have seen in the previous section. The three types of returns to scale are explained below.
Constant Returns to Scale
If outputs increase in the same proportion as the increase in inputs, returns to scale are said to be constant. Thus, doubling of all factor inputs causes doubling of the level of outputs; trebling of inputs causes trebling of outputs, and so on. The case of constant returns to scale is sometimes called linear homogenous production function. This is illustrated with the help of isoquants in fig. Where the line OE is the scale line. The scale line indicates the increase in scale. It can be observed from fig. That the distance between successive isoquants is equal, that is, Oa=ab=bc. It means that if both labour and capital are increased in a given proportion the output expands in the same proportion as the numbers 100,200 and 300 against the isoquants indicate.
Increasing Returns to Scale
When the output increases at a greater proportion than the increase in inputs, returns to scale are said to be increasing. It is explained in fig. When the returns to scale are increasing the distance between successive isoquants becomes less and less, that is Oa>ab>bc. It means tht equal increases in output, i.e. 100 unit at each isoquants are obtained by smaller and smaller increments in inputs. In other words, by doubling inputs the output is more doubled.
Increasing returns to scale arise on account of indivisibilities of some factors. As output is increased the indivisible factors are better utilized and therefore, increasing returns to scale arise. In other words, the returns to scale are increasing due to economies of scale.
Decreasing Returns to Scale
When the output increases in a smaller proportion than the increase in all inputs returns to scale re said to be decreasing. It is explained in fig.
It can be seen from fig. That the distance between successive isoquants are increasing, that is, Oa<ab<bc. It means that equal increments that is 100 units, in output are obtained by larger and larger increases in inputs. In other words, if the inputs are doubled, output will increase by less than twice its original level. The decreasing returns to scale are caused by diseconomies of large scale production.
An iso-product curve is locus of various combinations of two factors of production giving the same level of output and a producer is indifferent to each of such combinations. All the combinations of two inputs give the same quantum of output to a producer and the producer is indifferent to each such combination. He does not have any preference. These iso-product curves are also called production indifference curves. The concept of iso-product curve can be explained with the help of iso-quant schedule and diagram.
Iso-Quant Schedule:
An iso-quant schedule shows different combinations of two factors of production (inputs) at which a producer gets equal quantum of output.
A monopolistic firm is a price-maker, not a price-taker. Therefore, a monopolist can increase or decrease the price. Also, when the price changes, the average revenue, and marginal revenue changes too. Take a look at the table below:
Quantity Sold Price per unit Total Revenue
(TR) Average Revenue
(AR) Marginal revenue
(MR)
1 6 6 6 6
2 5 10 5 4
3 4 12 4 2
4 3 12 3 0
5 2 10 2 -2
6 1 6 1 -4
Let’s look at the revenue curves now:
Monopoly definition
As you can see in the figure above, both the revenue curves (Average Revenue and Marginal Revenue) are sloping downwards. This is because of the decrease in price. If a monopolist wants to increase his sales, then he must reduce the price of his product to induce:
The existing buyers to purchase more
New buyers to enter the market
Hence, the demand conditions for his product are different than those in a competitive market. In fact, the monopolist faces demand conditions similar to the industry as a whole.
Therefore, he faces a negatively sloped demand curve for his product. In the long-run, the demand curve can shift in its slope as well as location. Unfortunately, there is no theoretical basis for determining the direction and extent of this shift.
Talking about the cost of production, a monopolist faces similar conditions that a single firm faces in a competitive market. He is not the sole buyer of the inputs but only one of the many in the market. Therefore, he has no control over the prices of the inputs that he uses.
Introduction
A profit maximizing firm needs to monitor continuously about its cost and revenue. It is level of cost relative to revenue that determines the overall profitability of the firm. In order to maximise profits a firm has to increase its revenue and lower its cost.
Money Cost – Implicit and Explicit
- Implicit costs (IC) are due to the factors which the entrepreneur himself oens and employs in the firm.
- Explicit costs (EC) are the contractual cash payments made by the firm for purchasing or hiding the various factors.
Fixed, Variable and Total Cost
Fixed Cost
Total cost of production consists of fixed cost and variable cost.
Fixed costs are those which is independent of output. They must be paid even if the firm produces no output. They will not change even if output changes. They remain fixed whether output is large or small. Fixed costs are also called “overhead costs” or “supplementary costs”. They include such payments as rents, interest, insurance, depreciation charges maintenance costs, property taxes, administrative expense like manager’s salary and so on.
Variable Cost
Variable cost are those which are incurred on the employment of variable factors of production. They vary with the level of output. They increase with rise in output and decrease with the fall in output. By definition variable costs remain zero when output is zero. They include payments for wages, raw materials, fuel, power, transport and the like. Marshall called these variable costs as “Prime Costs” of production.
Average Total Cost (ATC)
One of the most important cost concept is average total cost. It, when compared with price or average revenue, will allow a business to determine whether or not it is making a profit. Average total cost is total cost divided by the number of unts produced i.e.
Average Total Cost = 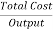 =
= 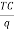 =ATC
=ATC
Where q represents the number of units of output produced.
Marginal Cost (MC)
Marginal Cost is the extra or additional cost of producing on extra unit of output. In economics the term ‘marginal’ whether applied to utility, cost, production, consumption or whatever, means ‘incremental’ or ‘extra’. Thus, marginal cost is the cost is the total cost of n units of output minus the total cost of n-1 units. In symbols:
MCn = TCn – TCn-1
Books Recommended :
1. Dewett K. K.—Adhunik Arth Shastra Ke Sidhant (Modarn Econoinic Theory).
2. Marshall—Principles of Economics.
3.Roy, L. M.—Arthshastra.
4. Sundharam K. P. M. And Vaish M. C.—Principles of Economics.
5. Stonier and Hague -A Text Book of Economic Theory.
6. Jain K. P.—Arthshastra Ke Sidhanta.
7. Ahuja, H. L.—Advanced Economic Theory,
8. Ahuja, H. L.—Uchatar Arthic Sidhanta