UNIT 6

Elementary mathematics

6.1Elementary ideas of AP, CP, HP

Arithmetic Progression

Arithmetic Progression Define

An A.P. Is referred as a sequence in which terms increase or decrease by a fixed number referred as common difference of the A.P.

AP. Sequence is expressed as a, a + d, a + 2d, …..

a: first term, d: common difference

Nth Term formula

an = a + (n-1)d

an: nth term, n: number of terms

Sn Sum of the 1st n terms

Sn = n/2(2a+(n-1)d)  = n/2 (a + l)

l= last term

To each term of a given A.P. a fixed number is added or subtracted or multiplied or divided the resulting sequence is an AP with a common difference d.

Consider 2 AP’s a1, a2, a3….. And b1, b2, b3….. With common differences d and d’ respectively then a1+b1, a2+b2, a3+b3…. Is also an A.P. With common difference d + d’

General combination of 3 terms in an A.P. a – d, a, a + d.

General combination of 4 terms in an A.P. a – 3d, a – d, a + d, a + 3d.

In case a1, a2, a3,…… an are in A.P. Then relation will be a1 + an = a2 + an-1 = a3 + an-2 = ……

If nth term of a sequence is a linear expression in n, the sequence will be an AP; its common difference will be coefficient of n.

In case sum of n terms of a sequence is a quadratic in n, its constant term is zero, the sequence will be an AP, its common difference is twice the coefficient of n2. If constant term is non-zero, it will be an .A.P. From 2nd term onwards.

Example 1

Find the value of n. If a = 10, d = 5, an = 95.

Solution

Given, a = 10, d = 5, an = 95

From the formula of general term, we have:

an = a + (n − 1) × d

95 = 10 + (n − 1) × 5

(n − 1) × 5 = 95 – 10 = 85

(n − 1) = 85/ 5

(n − 1) = 17

n = 17 + 1

n = 18

Example 2

Find the 20th term for the given AP:3, 5, 7, 9, ……

Solution: Given,

3, 5, 7, 9, ……

a = 3, d = 5 – 3 = 2, n = 20

an = a + (n − 1) × d

a20 = 3 + (20 − 1) × 2

a20 = 3 + 38

⇒a20 = 41

Example 3:

Find the sum of first 30 multiples of 4.

Solution: Given, a = 4, n = 30, d = 4

We know,

S = n/2 [2a + (n − 1) × d]

S = 30/2[2 (4) + (30 − 1) × 4]

S = 15[8 + 116]

S = 1860

Example 4 –

How many terms are added  in 24+20+16+ ....... 10 make the sum 72.

Solution

We know that sum to first n terms of an A.P. = Sn = n/2 [2a + (n – l) d]
Let the sum of n terms be 72,  a = 24,  d = -4

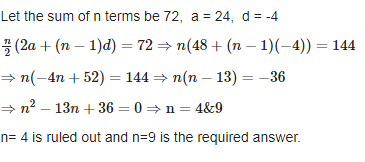
Key takeaways - The behavior of the arithmetic sequence depends on the common difference 

Geometric Progression

G.P. Is a sequence its 1st term is non-zero and its succeeding terms is r times the previous term, r is a fixed non-zero number called as the common ratio of the G.P.

Nth Term and Sum of n Terms:

‘a’ : 1st term, ‘r’ : common ratio

G.P. Is a, ar, ar2, …..

Nth Term ‘an’ is specified as an = arn-1

Sum Sn of the 1st n terms of the G.P. Is

Sn = [a(rn -1)]/(r-1) ; r ≠1

= na, r =1

Consider -1< r <1,

Sum of the infinite G.P. Is

a + ar + ar2 + ……= a/(1-r).

In case each term of a G.P. Is multiplied by a fixed non-zero constant, the resulting sequence is a G.P. With a common ratio.

If each term of a G.P. Is increased to the power k, the resulting sequence will be a  G.P. With common ratio rk.

a1, a2, a3…… is a G.P. With common ratio r.

b1, b2, b3…… is a G.P. With common ratio r’.

The sequence will be a1b1, a2b2, a3b3 is a G.P. With common ratio rr’.

Consider 3 terms in G.P. As a/r, a, ar. In case we have to take (2k+1) terms in a                 

G.P. We take a/rk, a/rk-1, a, ar, ark

For 4 terms in a G.P. We take a/r3, a/r, ar, ar3. For 2k terms in a G.P. We take

a/r2k-1, a/r2k-3, ……., a/r, ar, ….ar2k-1

If a1, a2,…..,an are in G.P. Then a1 an = a2 an-1   = a3 an-2 = …..

If a1, a2, a3, ………. Is a G.P. Then loga1, loga2, loga3…… is an AP. The converse is also true.

If {tn} is a G.P. Then the common ratio r = (tp/tq)1/p-q

Harmonic Progression (H.P.)

If the sequence 1/a1, 1/a2, 1/a3, …..1/an, ……, is an AP then the sequence a1, a2, a3……an….

(ai ≠ 0) is said to be an H.P.

Nth Term of H.P.

Sum of n terms,

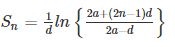
Where,

“a” is the first term of A.P

“d” is the common difference of A.P

“ln” is the natural logarithm Examples 1

If the first term is 10 and the common ratio of a GP is 3. Then write the first five terms of GP.

Solution: Given,

First term, a = 10

Common ratio, r = 3

We know the general form of GP for first five terms is given by:

a, ar, ar2, ar3, ar4

a = 10

Ar = 10 x 3 = 30

Ar2 = 10 x 32 = 10 x 9 = 90

Ar3 = 10 x 33 = 270

Ar4 = 10 x 34 = 810

Therefore, the first five terms of GP with 10 as first term and 3 as common ratio is:

10, 30, 90, 270 and 810

Examples 2

The sum of three numbers in a GP is 26 and their product is 216. Find the numbers.

Solution : Let the numbers be a/r, a, ar.

=> (a / r) + a + a r = 26

=> a (1 + r + r2) / r = 26

Also, it is given that product = 216

=> (a / r) x (a) x (a r) = 216

=> a3 = 216

=> a = 6

=> 6 (1 + r + r2) / r = 26

=> (1 + r + r2) / r = 26 / 6 = 13 / 3

=> 3 + 3 r + 3 r2 = 13 r

=> 3 r2 – 10 r + 3 = 0

=> (r – 3) (r – (1 / 3) ) = 0

=> r = 3 or r = 1 / 3

Thus, the required numbers are 2, 6 and 18.

Examples 3

Find the number of terms in the geometric progression 6, 12, 24, ..., 1536

Solution

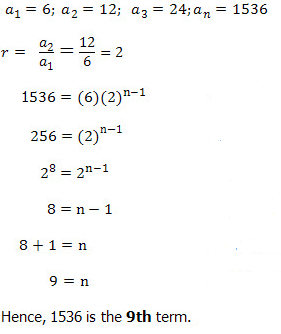
Examples 4

Determine the 4th and 8th term of the harmonic progression 6, 4, 3,…

Solution:

Given:

H.P = 6, 4, 3

Now, let us take the arithmetic progression from the given H.P

A.P = ⅙, ¼, ⅓, ….

Here, T2 -T1 = T3 -T2 = 1/12 = d

So, in order to find the 4th term of an A. P, use the formula,

The nth term of an A.P = a+(n-1)d

Here, a = ⅙, d= 1/12

Now, we have to find the 4th term.

So, take n=4

Now put the values in the formula.

4th term of an A.P = (⅙) +(4-1)(1/12)

= (⅙)+(3/12)

= (⅙)+ (¼)

= 5/12

Similarly,

8th term of an A.P = (⅙) +(8-1)(1/12)

= (⅙)+(7/12)

= 9/12

Since H.P is the reciprocal of an A.P, we can write the values as:

4th term of an H.P = 1/4th term of an A.P = 12/5

8th term of an H.P = 1/8th term of an A.P = 12/9 = 4/3

Examples 5

Compute the 16th term of HP if the 6th and 11th term of HP are 10 and 18 respectively.

Solution:

The H.P is written in terms of A.P are given below:

6th term of A.P = a+5d = 1/10 —- (1)

11th term of A.P = a+10d = 1/18 ……(2)

By solving these two equations, we get

a =13/90, and d = -2/ 225

To find 16th term, we can write the expression in the form,

a+15d = (13/90) – (2/15) = 1/90

Thus, the 16th term of an H.P = 1/16th term of an A.P = 90

Therefore, the 16th term of the H.P is 90.

Key takeaways - Geometric Progression refers to the numbers taken in a specific order. Harmonic progression is the reciprocal of arithmetic progression

6.2           Permutation and Combination

Permutation and combination are very important concept in mathematics. It represent a group of objects by selecting them in a set and forming subsets. It defines the various ways to arrange a certain group of data. Permutations  refers to when we select the data or objects from a certain group, whereas the order in which they are represented is called combination.

Permutation

In mathematics, permutation relates to the act of arranging all the members of a set into some sequence or order. Permutations occur, in more or less prominent ways, in almost every area of mathematics. They often arise when different orderings on certain finite sets are considered.

Combination

The combination is a way of selecting items from a collection, such that (unlike permutations) the order of selection does not matter. Combination refers to the combination of n things taken k at a time without repetition.

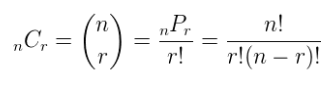
Example 1

Find the number of permutations and combinations if n = 12 and r = 2.

Solution:

Given,

n = 12

r = 2

Using the formula given above:

Permutation:

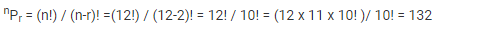
Combination:

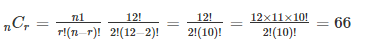
Key takeaways - The study of permutations and combinations is concerned with determining the number of different ways of arranging and selecting objects out of a given number of objects, without actually listing them.

6.3           Binomial Theorem, logarithmic, exponential series

Binomial Theorem

The Binomial Theorem is the method of expanding an expression which has been raised to any finite power. A binomial Theorem is a powerful tool of expansion, which has application in Algebra, probability, etc.

Let n ∈ N,x,y,∈ R then

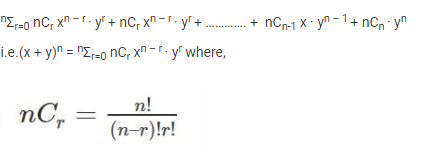
General term in binominal expansion

We have (x + y)n = nC0 xn + nC1 xn-1 . y + nC2 xn-2 . y2 + … + nCn yn

General Term = Tr+1 = nCr xn-r . yr

• General Term in (1 + x)n is nCr xr
• In the binomial expansion of (x + y)n , the rth term from end is (n – r + 2)th .

Example 1

Expand (x/3 + 2/y)4

Solution

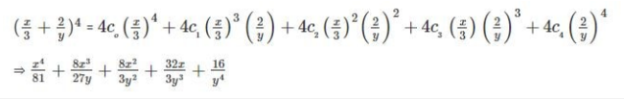
Example 2

Using binominal theorem , (√2 + 1)5 + (√2 − 1)5

Solution

We have

(x + y)5 + (x – y)5 = 2[5C0  x5 + 5C2  x3 y2  +  5C4 xy4]

= 2(x5 + 10 x3 y2 + 5xy4)

Now (√2 + 1)5 + (√2 − 1)5 = 2[(√2)5 + 10(√2)3(1)2 + 5(√2)(1)4]

=58√2

Example 3

Find the number of terms in (1 + 2x +x2)50

Solution

(1 + 2x + x2)50 = [(1 + x)2]50 = (1 + x)100

The number of terms = (100 + 1) = 101

Example 4

Find the fourth term from the end in the expansion of (2x – 1/x2)10

Solution

Required term =T10 – 4 + 2 = T8 = 10C7 (2x)3 (−1/x2)7 = −960x-11

Key takeaways - The Binomial Theorem is the method of expanding an expression which has been raised to any finite power

Logarithmic

Logarithm, the exponent or power to which a base must be raised to yield a given number.

Expressed mathematically, x is the logarithm of n to the base b if bx = n, in which case one writes x = logb n.

Examples1

Rewrite exponential function 72 = 49 to its equivalent logarithmic function.

Solution

Given 72 = 64.

Here, the base = 7, exponent = 2 and the argument = 49. Therefore, 72 = 64 in logarithmic function is;

⟹ log 7 49 = 2

Example 2

Write the logarithmic equivalent of 53 = 125.

Solution

Base = 5;

Exponent = 3;

And argument = 125

53 = 125 ⟹ log 5 125 =3

Example 3

Solve for x in log 3 x = 2

Solution

Log 3 x = 2
32 = x
⟹ x = 9

Example 4

If 2 log x = 4 log 3, then find the value of ‘x’.

Solution

2 log x = 4 log 3

Divide each side by 2.

Log x = (4 log 3) / 2

Log x = 2 log 3

Log x = log 32

Log x = log 9

x = 9

Example 5

Find the logarithm of 1024 to the base 2.

Solution

1024 = 210

Log 2 1024 = 10

Key takeaways - Logarithm, the exponent or power to which a base must be raised to yield a given number.

Exponential series

The function y = e x can also be written as a series :

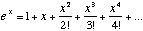Example 1

Write e3x as an exponential series for the first four terms.

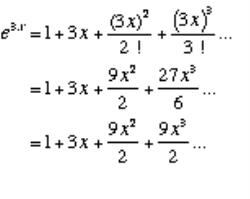
This means that the polynomial expression above, called a power series is a close approximation for ex.

The General Term of the Exponential Series

The general term of the exponential series is given by:

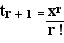Example 2

Find the 7th term for the exponential series e2x

Solution

t 7 = t 6+1 =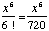 

6.4           Set Theory—definitions, Union intersection and difference of sets.

Set Theory is a branch of mathematics in which we study about sets and their properties. Georg Cantor (1845-1918), a German mathematician, initiated the concept ‘Theory of sets’ or ‘Set Theory’.

Definition

A set is any collection of objects specified in such a way that we can determine whether a given object is or is not in the collection.  In other words a set is the collection of objects. These objects are called elements or members of the set.

The following points are noted while writing a set

• Set are usually denoted by capital letters A, B, S, etc.
• The elements of the set are usually denoted by small letters a, b, t, etc

Examples –

A = {a, b,c, d}

C = {maths, science, history, English}

The symbol 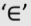is used to denote belongs to or is an element of or is a member of a set.

a is an element of set A

a is not an element of set A

Representation of set

1. Statement form - In this form, the well-defined description of the elements of the set is given.

Ex - The set of all even number less than 10.

2.     Roaster form - In this form, elements are listed within the pair of brackets {} and are separated by commas

Ex -  Let N is the set of natural numbers less than 5.

N = { 1 , 2 , 3, 4 }.

3.     Set builder form - In Set-builder set is described by a property that its member must satisfy.

1. {x : x is even number divisible by 6 and less than 100}

Types of sets

1. Empty sets – the sets that contains no members is called empty sets or null sets. The empty set is written as { }
2. Equal sets - Two sets are said to be equal if both have same elements. For example A = {1, 3, 9, 7} and B = {3, 1, 7, 9} are equal sets.
3. Subsets – sets which are the part of another set is called subsets of the original sets. Ex – if A = {1,2,3,4} and B  = {1,2}. Then B is the subset of A
4. Power set – if ‘A’ is any set then one set of all are subset of A that it is called a power set. Ex - What is the power set of {0,1,2}?

Solution: All possible subsets

{∅}, {0}, {1}, {2}, {0,1}, {0,2}, {1,2}, {0,1,2}.

Key takeaways - Set theory, branch of mathematics that deals with the properties of well-defined collections of objects such as numbers or functions.

Union Intersection and Difference of Sets

The union of two sets contains all the elements contained in either set (or both sets).

The union is notated A ⋃ B. A∪B={x:x∈A  or  x∈B}

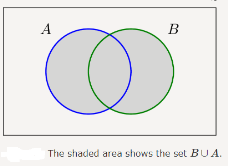
The intersection of two sets contains only the elements that are in both sets.

The intersection is notated A ⋂ B. A∩B={x:x∈A  and x∈B}

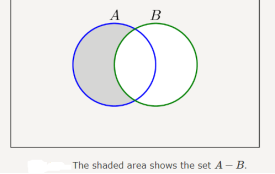
The difference is the set of all things that are in A but not in B.

A−B={x:x∈A  and x∉B}

Example 1

Consider the sets:       A = {red, green, blue}             B = {red, yellow, orange}

Find A ⋃ B, A ⋂ B, A-B

Solution

Find A ⋃ B

The union contains all the elements in either set: A ⋃ B = {red, green, blue, yellow, orange}

Note we only list red once

Find A ⋂ B

The intersection contains all the elements in both sets: A ⋂ B = {red}

Find A-B

The difference contains A-B = {green, blue}

Example 2

A={a,b,c,d,e} ,  B={d,e,f}  and  C={1,2,3} .

Solution

A∪B={a,b,c,d,e,f}

A∩B={d,e}

A−B={a,b,c}

B−A={f}

(A−B)∪(B−A)={a,b,c,f}

A∪C={a,b,c,d,e,1,2,3}

A∩C={∅}

A−C={a,b,c,d,e}

(A∩C)∪(A−C)={a,b,c,d,e}

(A∩B)×B={(d,d),(d,e),(d,f),(e,d),(e,e),(e,f)}

(A×C)∪(B×C)={(d,1),(d,2),(d,3),(e,1),(e,2),(e,3)}

Example 3

Suppose H = {cat, dog, rabbit, mouse}, F = {dog, cow, duck, pig, rabbit}

W = {duck, rabbit, deer, frog, mouse}

a)     Find (H ⋂ F) ⋃ W

b)    Find H ⋂ (F ⋃ W)

Solution

a) Find (H ⋂ F) ⋃ W

We start with the intersection: H ⋂ F = {dog, rabbit}

Now we union that result with W: (H ⋂ F) ⋃ W = {dog, duck, rabbit, deer, frog, mouse}

b) Find H ⋂ (F ⋃ W)

We start with the union: F ⋃ W = {dog, cow, rabbit, duck, pig, deer, frog, mouse}

Now we intersect that result with H: H ⋂ (F ⋃ W) = {dog, rabbit, mouse}

Example 4

If the universal set is given by S={1,2,3,4,5,6}, and A={1,2}, B={2,4,5},C={1,5,6} are three sets, find the following sets:

A∪B

A∩B

A

B

Solution

A∪B={1,2,4,5}.

A∩B={2}.

A ={3,4,5,6} (A  consists of elements that are in S but not in A).

B ={1,3,6}.

Key takeaways - the union A∪B is the set of all things that are in A or in B (or in both). The intersection A∩B is the set of all things in both A and B. The difference A−B is the set of all things that are in A but not in B.

6.5           Variables, Functions and Graphs Differentiation and integration functions

Variables and functions

Definition:

A function is a mathematical relationship in which the values of a single dependent variable are determined by the values of one or more independent variables. Function means the dependent variable is determined by the independent variable(s).

Variables

A variable is an alphabet which is used to represent the unknown number. It represents the value.

For example, x + 5 = 10

Here “x” is a variable.

Types of variables

Dependent Variable - The dependent variable is a variable that depends on the value of some other number or variable. In short, the dependent variable is the output of a function. The value of the dependent variable changes, if there is a change in the value of an independent variable

Example: y = 4 + 2x

Here, y is called a dependent variable. The value of y completely depends on the function 4 + 2x

Independent Variable -The independent variable does not depend on any values. It is called the input of a function. The value of the independent variable is not affected by any values of a function.

Example: x = 2y + 3z

Here, x is called a dependent variable

y and z are the independent variables

Examples

Find the value of the variable y for the equation y = 2x2  when x = 5

Solution:

Given equation: y = 2x2

Here x is called independent variable

Y is called dependent variable

When x = 5, the value of y becomes:

y = 2x2

Now, substituting x = 5 in the given equation, we get

y = 2(5)2

y = 2(25)

y = 50

Therefore, the value of y is 50, when x = 5

Example

Two or more functions can be added, subtracted, multiplied or divided.

g(x) = x - 3                   h(x) = x2 + 2

Find g(0) + h(0)

g(0) = 0 - 3 = -3

h(0) = 02 + 2 = 2

g(0) + h(0) = -3 + 2 = -1

Find g(1) h(2)

g(1) = 1 - 3 = -2

h(2) = 22 + 2 = 6

g(1) h(2) = (-2) ( 6) = -12

Example

y = f(x) = 3x + 4

Find f(0), Find f(1), Find f(-1)

Solution

Find f(0). This means find the value of y when x equals 0.

f(0) = 3 times 0 plus 4

f(0) = 3(0) + 4 = 4

Find f(1). This means find the value of y when x equals 1.

f(1) = 3 times 1 plus 4

f(1) = 3(1) + 4 = 7

Find f(-1). This means find the value of y when x equals -1.

f(-1) = 3 times (-1) plus 4

f(1) = 3(-1) + 4 = 1

Key takeaways - A function is a mathematical relationship in which the values of a single dependent variable are determined by the values of one or more independent variables

Graphs Differentiation and integration functions

Definition of Differentiation

A derivative of a function related to the independent variable is called Differentiation and it is used to measure the per unit change in function in the independent variable. If y = f(x) is a function of x, then the rate of change of y per unit change in x is given as:

Important Differentiation Formulas

Definition of Integration

The integration of a function f(a) is given by F(a) and is written as

∫ f(a) da = F(a) +C, where Right hand side shows integral of f(a) with respect to a

F(a) is called primitive, f(a) is called the integrand and C is constant of integration, a is variable.

Important Integration Formulas

Example 1: 

Find the derivative of x2cos x.

Solution:

Let f(x) = x2 cos x

Differentiate the given function with respect to x,

f’(x) = d/dx (x2 cos x)

= x2 d/dx(cos x) + cos x d/dx(x2)

= x2 (-sin x) + cos x (2x)

= 2x cos x -x2 sin x

Example 2: 

Find the derivative of f(x) = x + sin x.

Solution:

Given function is f(x) = x + sin x

Differentiate with respect to x,

f’(x) = d/dx(x + sin x)

= d/dx(x) + d/dx (sin x)

= 1 + cos x

Example 3: 

Evaluate: ∫7 cos x dx

Solution:

∫7 cos x dx

= 7 ∫cos x dx

= 7 sin x + C

Example 4: 

Evaluate:  ∫6 sin 3x dx

Solution:

∫6 sin 3x dx

= 6  ∫ sin 3x dx …..(i)

Let u = 3x  …..(ii)

Du = 3dx

Dx = ⅓ du …..(iii)

From (i), (ii) and (iii),

= 6  ∫sin u (⅓) du

= (6/3)  ∫ sin u du

= 2 (-cos u) + C

Substituting u =  3x in the above step,

= -2 cos 3x + C

Key takeaways - Differentiation is used for calculating the derivatives. Integration is the process to calculate definite or indefinite integrals.

6.6           Elementary idea of Determinaters, Matrices and Vectors up to purchase of two vectors.

Elementary Ideas of Determinations and Matrices

Matrices

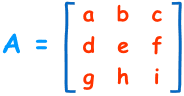
Set of numbers or objects or symbols represented in the form of the rectangular array is called a matrix.

For example 

Matrix   has 2 rows and 3 columns so its order is said to be 2 × 3.

Determinates

The determinant of a matrix: a number which is calculated from the matrix. For determinant to exist, matrix A must be a square matrix. The determinant of a matrix is denoted by det A or |A|.

For a 2×2 Matrix

For a 2×2 matrix (2 rows and 2 columns):

The determinant is:

|A| = ad – bc

"The determinant of A equals a times d minus b times c"

For a 3×3 Matrix

For a 3×3 matrix (3 rows and 3 columns):

The determinant is:

|A| = a(ei − fh) − b(di − fg) + c(dh − eg)
"The determinant of A equals ... Etc"

Operations on matrices

Addition and subtraction – two matrices may be added if they are in same order

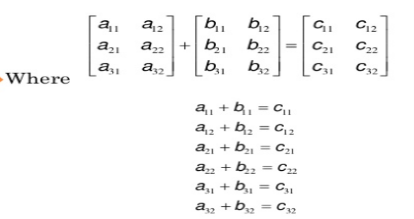
Scalar multiplication – to multiply scalar times a a matrix, simply multiplying each element of the matrix by the scalar quantity

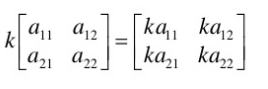
Multiplication matrix - We can only multiply matrices if the number of columns in the first matrix is the same as the number of rows in the second matrix.

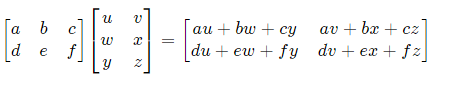
Example 1

Multiply matrix

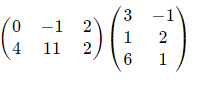
Solution

This is 2×3 times 3×2, which will give us a 2×2 answer

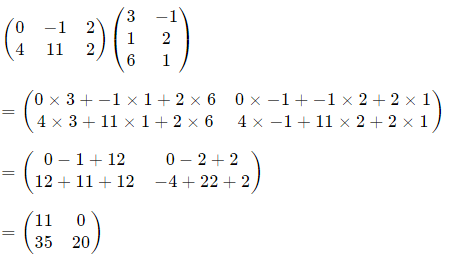
Our answer is a 2×2 matrix.

Example 2

Multiply matrix

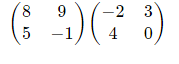
Solution

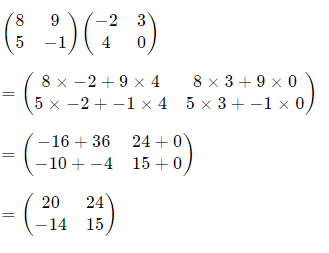
Example 3

If possible, find BA and AB

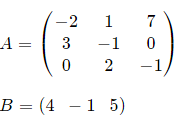
Solution

AB is not possible. (3 × 3) × (1 × 3)

Example 3

Calculate the determinants of

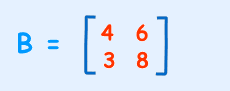
Solution

B    = 4*8 – 6*3

= 32 – 18 = 14

Example 4

Calculate the determinants of

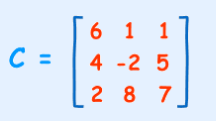
Solution

C  = 6×(−2×7 − 5×8) − 1×(4×7 − 5×2) + 1×(4×8 − (−2×2))

= 6×(−54) − 1×(18) + 1×(36)

= −306

Vectors

Vectors up to purchase of two vectors.

A vector has magnitude (size) and direction:

The length of the line shows its magnitude and the arrowhead points in the direction.

Adding vector

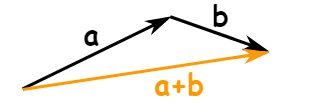
Example 1

Example: add the vectors a = (8, 13) and b = (26, 7)

Solution

c = a + b

c = (8, 13) + (26, 7) = (8+26, 13+7) = (34, 20)

Example 2

Add the vectors a = (3, 7, 4) and b = (2, 9, 11)

Solution

c = a + b

c = (3, 7, 4) + (2, 9, 11) = (3+2, 7+9, 4+11) = (5, 16, 15)

Key takeaways – The determinant of a matrix is a special number that can be calculated from a square matrix

6.7 Coordinates, St. Lines, pair of St lines

Coordinates

A coordinate system is a two-dimensional number line, for example, two perpendicular number lines or axes.

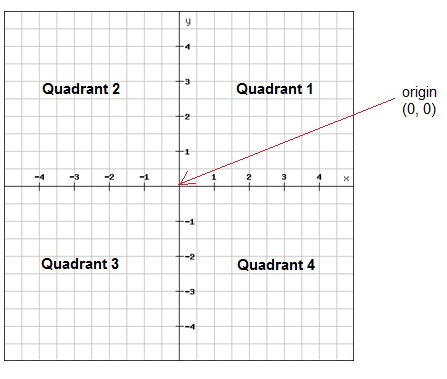
The horizontal axis is called the x-axis and the vertical axis is called the y-axis

The center of the coordinate system (where the lines intersect) is called the origin. The axes intersect when both x and y are zero. The coordinates of the origin are (0, 0).

An ordered pair contains the coordinates of one point in the coordinate system. A point is named by its ordered pair of the form of (x, y). The first number corresponds to the x-coordinate and the second to the y-coordinate.

Example

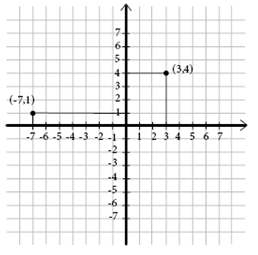
The ordered pair (3, 4) is found in the coordinate system when you move 3 steps to the right on the x-axis and 4 steps upwards on the y-axis.

The ordered pair (-7, 1) is found in the coordinate system when you move 7 steps to the left on the x-axis and 1 step upwards on the y-axis.

St lines

Definition

A line is simply an object in geometry that is characterized under zero width object that extends on both sides. A straight line is just a line with no curves. So, a line that extends to both sides till infinity and has no curves is called a straight line.

Equation

The equation of the straight line is y = mx + c, where m is the gradient, and y = c is the value where the line cuts the y-axis. Furthermore, the number c is called the intercept on the y-axis.

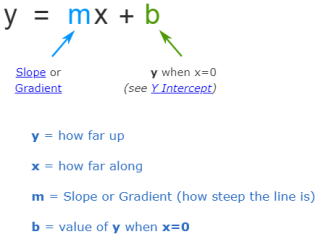
Pair of straight line

General equation

Consider the equations of two straight lines

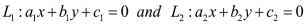
Their combined equation may be given by

. ......(1)

On multiplying the left hand side of (1), we get an equation of the form  ......(2)

Where a = a1a2, 2h = a1b2 + a2b1, ...... Etc.

The equation (2) is the most general equation of second degree, which will represent a pair of straight lines under certain conditions.

Homogenous equation of second degree

An equation of the type

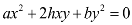 ......(3)

Is a homogeneous equation of second degree. [Note that the sum of the powers of x and y in every term is the same and 2].

The homogeneous equation of the second degree always represents a pair of straight lines passing through the origin. We have

1. If h2 > ab, the two lines are real and different
2. If h2 = ab, the two lines are coincident
3. If h2 < ab, the two lines are imaginary having origin as their real point of intersection.

If 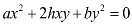represents the pair of lines y = m1x and y = m2x. Then

........(4)

Comparing the coefficients we get

and 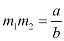........(5)

Key takeaways - A coordinate system is a two-dimensional number line. The equation of the straight line is y = mx + c

Sources

I.B. N. Gupta : Business Math & Statistics

II. S. P. Singh : Statistics

III. Mukund Lal : Statistics

IV. K. N. Nayar : Statistics

V. C. B. Gupta : Statistics

VI. Shukla & Sahay : Statistical Analysis

VII. C. D. Gupta : Statistical Analysis

VIII. D. N. Elhana : Statistical Analysis