UNIT 6

POWER TRANSMISSION SYSTEM

6.1 BELT DRIVES:

The belt drive is used to transmit power from one shaft to another by means of pulleys which rotate at the same speed or at different speed.

I) open and cross belt drive

1. Open Belt Drive:

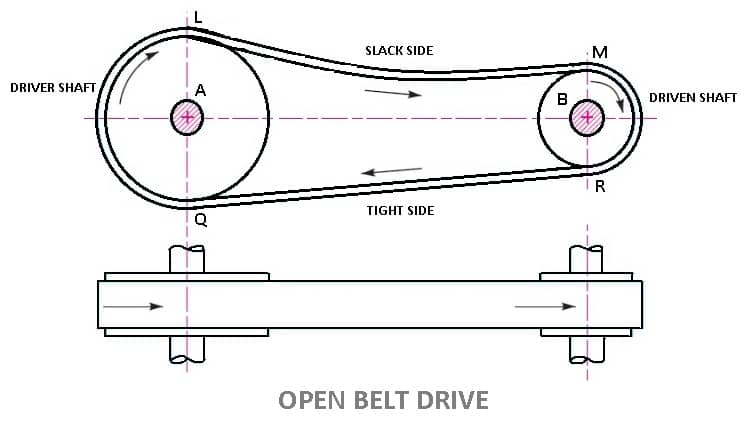
• In these types of belt drive, the belt is employing when the two parallel shafts have to rotate in the same direction.
• When the shafts are far apart, the lower side of the belt should be the tight side and the upper side must be the slack side.
• This is because, when the upper side becomes the slack side, it will sag due to its own weight and thus increase the arc of contact.
• In open belt drive, belt proceeds from top of one pulley to the top of other pulley without crossing.
• Contact angle (or wrap angle) between the belt and pulley is comparatively small (always below 180º in smaller pulley).

     LENGTH OF OPEN BELT DRIVE FORMULA:

= π (r1 + r2) + 2x + (r1 – r2)2 /x    ……………. (In terms of pulley radii)

= π/2 (d1 + d2) + 2x + (d1 – d2)2/ 4x ……….… (In terms of pulley diameters)

2. Cross Belt Drive

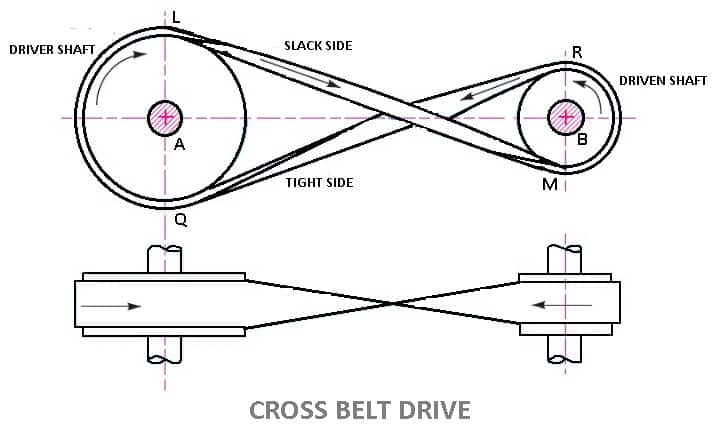
• In this type of belt drives, the belt is employing when two parallel shafts have to rotate in the opposite direction. At the junction where the belts cross, it rubs against itself and wears off.
• To avoid excessive wear, the shafts must be placed at a maximum distance from each other and operated at very low speeds.
• Contact angle between the belt and pulley is comparatively large (always above 180º in smaller pulley).
• In crossed belt drive, belt proceeds from top of one pulley to the bottom of other pulley and thus crosses itself.
• Here belt bends in two different planes in every rotation during its operation
• Cross belt drive can be advantageously applied for horizontal, inclined and vertical positions of driving and driven shafts.
• It can transmit more power as wrap angle is more.

LENGTH OF CROSS BELT DRIVE

= π (r1+r2) + 2x + (r1+r2)2 /x     …………… (In terms of pulley radii)

= π/2(d1+d2) +2x + (d1 + d2)2/ 4x …………(in terms of pulley diameters)

II) Material of belts:

The  Materials used  for  belts  and  ropes  must  be strong,  flexible,  and  durable. It must have high coefficient of friction: like

1- Leather belts

2- Cotton belts

3- Rubber belts

4- Balata belts

1. Leather belts :

The leather may be oak tanned or mineral salt tanned. Example chrome tanned. When the thickness of the belt required is more then, two or more strips are cemented together. Leather belts require periodic cleaning.

2. Cotton belts or Fabric belts :

Fabric belts are made by folding canvas or cotton ducks in layers and stitching together. The fabric belts are cheaper and best suited in warm climates, damp atmospheres. These are mostly used in Farm machinery, belt conveyor etc.

3. Rubber belts :

Rubber belts are made of Fabric with rubber layer. Rubber belts are used in sawmills, paper mills, etc.

4. Balata Belts:

Balata belts are similar to rubber belts except that balata gum is used in place of rubber. Balata belts are acid proof and water proof and it is not effected by animal oils or alkalies. The balata belts should not be at temperatures above 40° C because at this temperature the balata begins to soften and becomes sticky. The strength of balata belts is 25 percent higher than rubber belts.

III)  Type of belts:

Different types of belt are as follows

1. Flat Belt
2. V – Belt
3. Circular Belt

1. Flat Belt :

Flat belt has a rectangular cross section. Flat belts are capable of transmitting power over long distance between pulley centres. The efficiency of this drive is around 98 % and produces less noise.

This belt is mostly used in factories and workshops, where a moderate amount of power is to be transmitted, from one pulley to another when two pulleys are not more than 8 metres apart.

Flat belts drives are of following types:

1. Open belt drive.
2. Cross belt drive.
3. Stepped or cone pulley or speed cone drive.
4. Fast and loose pulleys.
5. Jockey pulley drive or belt drive with idler pulley
6. Compound Belt Drive System

2. V – Belt:

V-Belts also used with grooved pulleys, V-belts are trapezoidal in cross section. V-belts permit large speed ratios and can transmit higher power. Multiple drives are possible.

This belt is mostly used in factories and workshops, where a moderate amount of power is to be transmitted, from one pulley to another when two pulleys are very near to each other.

3. Circular Belt or Round Belt :

Circular Belt or Round belt has a circular cross section and is used with grooved pulleys, This belt is mostly used in factories and workshops, where a great  amount of power is to be transmitted, from one pulley to another when two pulleys are  more than 8 metres apart.

IV)  Length of belt of open and cross drive:

Length of Open belts drive:

We have discussed that in an open belt drive, both the pulleys rotate in the same direction as shown in Fig. 1.

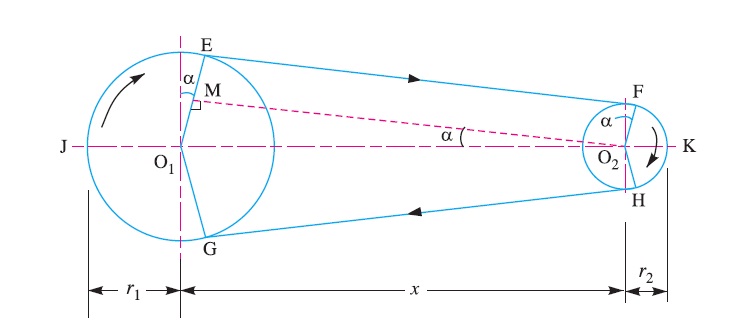
Let r1 and r2 = Radii of the larger and smaller pulleys,
x = Distance between the centres of two pulleys (i.e. O1O2), and
L = Total length of the belt.

Let the belt leaves the larger pulley at E and G and the smaller pulley at F and H as shown in Figure. Through O2 draw O2M parallel to FE.
From the geometry of the figure, we find that O2M will be perpendicular to O1E.

Let the angle MO2O1 = α radians.
We know that the length of the belt,
L = Arc GJE + EF + Arc FKH + HG
= 2 (Arc JE + EF + Arc FK)            ……………………..(i)
From the geometry of the figure, we also find that

Sin α = O1M/O1O2 = O1E – EM / O1O2 = r1 – r2 / x

Since the angle α is very small, therefore putting
sin α = α (in radians) = r1 – r2 / x        …………………….(ii)

∴ Arc JE = r1 (π/2 + α)            ………………………….(iii)

Similarly, arc FK = r2 (π/2 – α)             ……………………..(iv)

And EF = MO2 = [(O1O2)2 – (O1M)2]0.5

= [x2 – (r1 – r2)2]0.5

= x [1 – {(r1-r2) /x }2 ]0.5

Expanding this equation by binomial theorem, we have

EF = x [1 – {0.5 {(r1 – r2)/x} + …] = x – (r1 – r2)2 /2x            …………………..(v)

Substituting the values of arc JE from equation (iii), arc FK from equation (iv) and EF from equation (v) in equation (i), we get

L = 2 [r1(π/2 +α) + x – {(r1-r2)2/2x} + r2(π/2 -α)]

= 2 [{r1 × π/2} + {r1×α} + x – {(r1- r2)2/2x} + {r2 × π/2} - {r2×α}]

= 2 [π/2(r1+r2) + α(r1-r2) +x – {(r1-r2)2/2x}]

= π(r1+r2) + 2α(r1-r2) +2x – {(r1-r2)2/x}

Substituting the value of α = (r1-r2)/x from equation (ii), we get

L = π(r1+r2) + 2{(r1-r2)/x}{(r1-r2)} +2x – {(r1-r2)2/x}

= π(r1+r2) + 2{(r1-r2)2/x} + 2x – {(r1-r2)2/x}

= π (r1 + r2) + 2x + (r1 – r2 )2 /x                     ……………. (in terms of pulley radii)

=  π/2 (d1 + d2) + 2x + (d1 – d2)2 /4x                     …… (in terms of pulley diameters)

Length of cross belt drive:

We have discussed that in a cross belt drive, both the pulleys rotate in the opposite directions as shown in Fig
  Let r1 and r2 = Radii of the larger and smaller pulleys,
   x = Distance between the centres of two pulleys (i.e. O1O2 ), and
   L = Total length of the belt.
   Let the belt leaves the larger pulley at E and G and the smaller pulley at F and H as shown in Figure.
    Through O2 draw O2M parallel to FE.
     From the geometry of the figure, we find that O2M will be perpendicular to O1E.
       Let the angle MO2O1 = α radians.
       We know that the length of the belt,
         L = Arc GJE + EF + Arc FKH + HG
             = 2 (Arc JE + FE + Arc FK)             …………………(i)

From the geometry of the figure, we find that

Sin α = O1M/O1O2 = (O1E + EM)/O1O2 = r1+r2 / x

Since the angle α is very small, therefore putting  sin α = α (in radians                  = r1+r2 / x          ………………………….…(ii)

Arc JE = r1 (π/2 + α)  ………………. ……(iii)

Similarly, arc FK = r2 (π/2 + α)            …………………(iv)

EF = MO2 = [(O1O2 )2 – (O1M)2]0.5

= [x2 – (r1 + r2 )2]o.5

= x [1- (r1+r2 /x )2 ]0.5

Expanding this equation by binomial theorem, we have

EF = x [1- 1/2(r1+r2 /x)2 + …] = x – [(r1+r2)2/2x]     ……………………(v)

Substituting the values of arc JE from equation (iii), arc FK from equation (iv) and EF from equation (v) in equation (i), we get,

L = 2 [r1(π/2 +α) + x – {(r1+r2)2/2x} + r2(π/2 +α)]

= 2 [{r1 × π/2} + {r1×α} + x – {(r1+r2)2/2x} + {r2 × π/2} + {r1×α}]

= 2 [π/2(r1+r2) + α(r1+r2) +x – {(r1+r2)2/2x}]

= π(r1+r2) + 2α(r1+r2) +2x – {(r1+r2)2/x}

Substituting the value of α = (r1+r2)/x from equation (ii), we get

L = π(r1+r2) + 2{(r1+r2)/x}{(r1+r2)} +2x – {(r1+r2)2/x}

= π(r1+r2) + 2{(r1+r2)2/x} + 2x – {(r1+r2)2/x}

= π (r1+r2) + 2x + (r1+r2)2 /x     …………… (In terms of pulley radii)

= π/2(d1+d2) +2x + (d1 + d2)2/ 4x …………(in terms of pulley diameters)

V)               Velocity ration for simple and compound belt drive:

It is the ratio between the velocities of the driver and the follower or driven. It may be expressed, mathematically, as discussed below:
Let d1 = Diameter of the driver,
d2 = Diameter of the follower,
N1 = Speed of the driver in r.p.m.,
N2 = Speed of the follower in r.p.m.,
∴ Length of the belt that passes over the driver, in one minute

= π d1 N1

Similarly, length of the belt that passes over the follower, in one minute
= π d2 N2

Since, the length of belt that passes over the driver in one minute is equal to the length of belt that passes over the follower in one minute, therefore
= π d1 N1 = π d2 N2

And velocity ratio,

= N2/N1 = d1/d2

When thickness of the belt (t) is considered, then velocity ratio,

=  N2/N1 = (d1 + t)/ (d2 + t)

The velocity ratio of a belt drive may also be obtained as discussed below:
We know that the peripheral velocity of the belt on the driving pulley,

ν1 = (π d1 N1)/60, m/s

And peripheral velocity of the belt on the driven pulley,

ν2 = (π d2 N2)/60, m/s

When there is no slip, then ν1 = ν2.

(π d1 N1)/60 = (π d2 N2)/60

N2/N1 = d1/d2

In case of a compound belt drive, the velocity ratio is given by

= N4/N1 = (d1 × d3)/(d2 × d4)

= Speed of last driven / Speed of first driver = Product of diameters of drivers        / Product of diameters of drivens

VI)           Centrifugal tension:

The belt continuously runs over the pulleys, therefore, some centrifugal force is caused, whose effect is to increase the tension on both the tight as well as the slack sides. The tension caused by centrifugal force is called centrifugal tension.

At lower belt speeds (less than 10 m/s), the centrifugal tension is very small, but at higher belt speeds (more than 10 m/s), its effect is considerable and thus should be taken into account.

Consider a small portion PQ of the belt subtending an angle dθ at the centre of the pulley, as shown in FIG

.

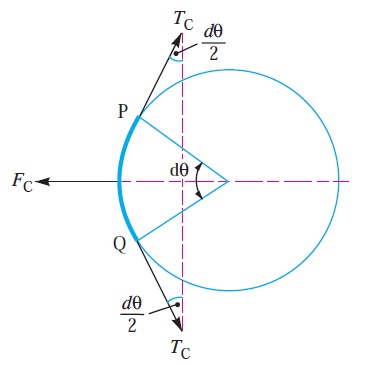
Let m = Mass of belt per unit length in kg,
v = Linear velocity of belt in m/s,
r = Radius of pulley over which the belt runs in metres, and
TC = Centrifugal tension acting tangentially at P and Q in newton’s.

We know that length of the belt PQ
                                                      = r.dθ
          and mass of the belt PQ = m.r.dθ
 

∴ Centrifugal force acting on the belt PQ,

FC = m.r.dθ × v2/r

= m.dθ.v2

The centrifugal tension TC acting tangentially at P and Q keeps the belt in equilibrium. Now resolving the forces (i.e. centrifugal force and centrifugal tension) horizontally, we have

Tc sin (dθ/2) + Tc sin (dθ/2) = Fc = = m.dθ.v2

Since the angle dθ is very small, therefore putting sin (dθ/2) = (dθ/2) in equation (i), we have

2Tc (dθ/2) = m.dθ.v2

Tc = m.v2

When centrifugal tension is taken into account, then total tension in the tight side,
                    Tt1 = T1 + Tc

And total tension in the slack side,
                    Tt2 = T2 + Tc

2. Power transmitted,
                     P = (Tt1 – Tt2) v                              …………………….(in watts)
                         = [(T1 + Tc) – (T2 + Tc)]v = (T1 – T2) v   ……… (same as before)

  we see that the centrifugal tension has no effect on the power transmitted.
 

The ratio of driving tensions may also be written as

2.3 log (Tt1-Tc / Tt2-Tc) = μ.θ

Where,

Tt1 = Maximum or total tension in the belt.

VII)      Maximum power transmitted:

Let T1  = Tension on tight side

T2 = Tension on slack side

v = Linear velocity of belt

Then the power transmitted can be given by the equation

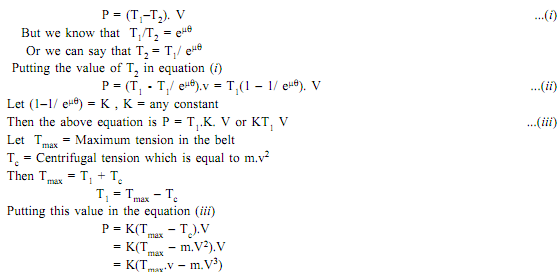
Power transmitted will be maximum if d (P)/dv = 0

Thus differentiating equation with respect to V and equating to zero for maximum power, we get

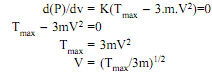
Equation (iv) gives velocity of belt at which maximum power is transmitted.

From equation (iv) Tmax  =3Tc                                                                                                                      ...(v)

Hence when power transmitted is maximum, the centrifugal tension would be around 1/3rd of the maximum tension.

We know that Tmax = T1  + Tc

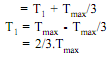
Hence condition for transmission of maximum power is:

Tc = 1/3 Tmax, and     

T1 =2/3Tmax                                                                                                                    ...(viii)The net driving tension in the belt = (T1  - T2)

6.2 Other transmission system

I)                 Chain drive :

We have seen in belts that slipping is occurs. In order to avoid slipping steel chains are used. The chain are made up of rigid links which are hinged together in order to provide the necessary flexibility for wrapping around the driving and driven wheel. The tooth wheels are known as sprocket wheels or simple sprockets.

A chain drive is a mechanically operating system where we used different types of chains to transmit the power or for movement of something.

Generally, a chain drive is used where the distance between the power produced and where it to be transferred is less, however, this is not applicable for all. In some cases, we can use a chain drive for longer distances power transfer.In belt or rope drive we see there is some percent of slip occurs, but in the chain, there will be no slip. But this does not mean that 100% power is transmitted from one to another device due to friction loss some amount of power loss we can generally see.

In chain drive, the speed ratio remains constant which is a major advantage of chain drive and here there is no slippage and in case of belt drive, there is slippage so speed ratio changes as per slippage. A chain is made by a number of links and those are connected by the help of a pin.

Chains are run over a wheel named sprocket which has several amounts of teeth around the circumference of that to grip the chain, however, not all the chains need that sprocket to run over

Types of Chains:

In the field of Mechanical Engineering chains drive can be classified into three broad categories and those are:

1. Hoisting Chains
2. Conveyor Chains
3. Power transmission Chains.

1)     HOISTING CHAINS:

A hoist is a mechanical device which is used to lift a load or lowering a load, it can be used for shifting of some heavy product from one place to another place in a workstation. The chains used in this type of devices is named hoist chain, these chains are quite strong to handle heavyweight.

Hoist chains can be classified into two categories:

1. Oval-Link Chains.

1. Stud-Link Chains.

i)                   Oval-Link Chains:

It is one of the common types of chain used in hoist; it consists of many oval links attached to each other. These types of chains are also called Coil Chains. Links of this type of chain is oval. However, there are square link types of chains that are also available, but the kinking is occurred easily due to high loading.

Ii)                Stud-Link Chains:

The stud-link chains used to minimize the deformation and link or tangle easily. In this type of chain, a round bar or stud is used to fit inside the oval-link chains to provide more strength to the chain. The stud-link chains used to minimize the deformation and link or tangle easily. In this type of chain, a round bar or stud is used to fit inside the oval-link chains to provide more strength to the chain. It is used in Ship to up and down the anchor of the ships, and some crane hoist where we need to lift a very high amount of load.

2)     CONVEYOR CHAINS:

As the name suggests conveyor chains that means these types of chains are mostly used in the conveyor. The conveyor is a mechanical device system that is used to move the materials from one place to another. This type of chain is well shaped that it can easily run over the sprocket. 

Generally, this type of chain is made of malleable cast iron and used in Low-Speed Machinery approx. 2 m/s.

The one major disadvantage of this type of chain is the motion of the chain is not smooth, there are chances of wear and tear out.

Conveyor Chains are categorized into following types:

1. Detachable or Hook Joint types Conveyor chain.
2. Closed-end pintle type conveyor chain.

1. Detachable or Hook Joint types Conveyor chain: Detachable or Hook Joint types Conveyor chains are used in a conveyor where the length between power transmissions is short.
2. Closed-end pintle type conveyor chain: This type of chain is consists of a barrel and link and made in a single casting, and then the chain is heat-treated to provide higher strength.

3)     POWER TRANSMISSION CHAINS:

You can easily find out by name of the chain that it is used to transmit the power. This type of chain is made of steel and sometimes it heats treated to minimize wear and tear. This type of chain has greater accuracy and can easily run over the sprocket.

II)             Gear:

A gear is a kind of machine element in which teeth are cut around cylindrical or cone shaped surfaces with equal spacing. By meshing a pair of these elements, they are used to transmit rotations and forces from the driving shaft to the driven shaft. Gears can be classified by shape as involute, cycloidal and trochoidal gears. Also, they can be classified by shaft positions as parallel shaft gears, intersecting shaft gears, and non-parallel and non-intersecting shaft gears.

III)         Type of gear:

Following are the different types of gears:

1. Parallel gears
   1. Spur Gears
   2. Helical Gears
   3. Double Helical or Herringbone Gears.
2. Intersecting gears
   1. Spiral gears
   2. Bevel Gears
3. Non-intersecting and Non-Parallel gears.
   1. Worm Gears
4. Rack and Pinion gears

1)     Parallel gears - As indicated by the name, parallel configurations involve gears connected to rotating shafts on parallel axes within the same plane. The rotation of the driving shaft (and the driving gear) is in the opposite direction to that of the driven shaft (and driven gear), and the efficiency of power and motion transmission is typically high.

a)     Spur gear:

Spur gears transmit power through shafts that are parallel. The teeth of the spur gears are parallel to the shaft axis. This causes the gears to produce radial reaction loads on the shaft, but not axial loads. Spur gears tend to be noisier than helical gears because they operate with a single line of contact between teeth.  While the teeth are rolling through mesh, they roll off of contact with one tooth and accelerate to contact with the next tooth.  This is different than helical gears, which have more than one tooth in contact and transmit torque more smoothly.

b) Helical Gear:

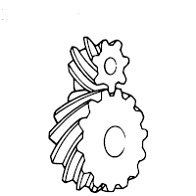
Helical gears have teeth that are oriented at an angle to the shaft, unlike spur gears which are parallel. This causes more than one tooth to be in contact during operation and helical gears are capable of carrying more load than spur gears. Due to the load sharing between teeth, this arrangement also allows helical gears to operate smoother and quieter than spur gears. Helical gears produce a thrust load during operation which needs to be considered when they are used. Most enclosed gear drives use helical gears.

c) Double Helical Gear:

Double helical gears are a variation of helical gears in which two helical faces are placed next to each other with a gap separating them.  Each face has identical, but opposite, helix angles. Employing a double helical set of gears eliminates thrust loads and offers the possibility of even greater tooth overlap and smoother operation. Like the helical gear, double helical gears are commonly used in enclosed gear drives.

d) Herringbone Gear

Herringbone gears are very similar to the double helical gear, but they do not have a gap separating the two helical faces. Herringbone gears are typically smaller than the comparable double helical, and are ideally suited for high shock and vibration applications. Herringbone gearing is not used very often due to their manufacturing difficulties and high cost.

2)     Intersecting gears

Bevel gear: Bevel gears are most commonly used to transmit power between shafts that intersect at a 90 degree angle. They are used in applications where a right angle gear drive is required. Bevel gears are generally more costly and are not able to transmit as much torque, per size, as a parallel shaft arrangement.

Bevel gear transmits power between two intersecting shafts at any angle or non-intersecting shaft. They are classified as straight and spiral tooth bevel and hypoid gears. These are gears cut from conical blanks and connect intersecting shaft axes.

The connecting shaft is generally at 90°and sometimes one shaft drives a bevel gear which is mounted on a through the shaft resulting in two output shafts. The point of intersection of the shaft is called the apex and the teeth if the two gears converge at the apex.

There are several types of bevel gears available differentiated mainly by their tooth design. Some of the more common types of bevel gears include straight, spiral, and Zero bevel gears.

a)     Straight Bevel Gears

The most commonly used of the bevel gear tooth designs due to its simplicity and, consequently, its ease of manufacturing, straight bevel teeth are designed such that when properly matched straight bevel gears come into contact with one another, their teeth engage together all at once rather than gradually. As is the issue with spur gears, the engagement of straight bevel gear teeth results in high impact, increasing the level of noise produced and amount of stress experienced by the gear teeth, as well as reducing their durability and lifespan.

b)    Spiral Bevel Gears

In spiral bevel gears, the teeth are angled and curved to provide for more gradual tooth engagement and more tooth-to-tooth contact than with a straight bevel gear. This design greatly reduces the vibration and noise produced, especially at high angular velocities (>1,000 rpm). Like helical gears, spiral bevel gears are available with right-hand or left-hand angled teeth. As is also the case with helical gears, these gears are more complex and difficult to manufacture (and, consequently, more expensive), but offer greater tooth strength, smoother operation, and lower levels of noise during operation than straight bevel gears.

Additional Bevel Gear Designs

Other than the types mentioned above, there are several other designs of bevel gears available including miter, crown, and hypoid gears.

c)     Miter: Miter gears are bevel gears which, when paired, have a gear ratio of 1:1. This gear ratio is a result of pairing two miter gears with the same number of teeth. This type of bevel gear is used in applications which require a change only to the axis of rotation with speed remaining constant. When two bevel gear has their axes at right angles and is equal sizes, they are called mitre gears.

d)    Crown: Crown gears, also referred to as face gears, are cylindrical (rather than conical) bevel gears with teeth cut or inserted perpendicular to the gear face. Crown gears can be paired either with other bevel gears or, depending on the tooth design, spur gears.

e)     Hypoid: Originally developed for the automobile industry, hypoid gears, unlike the previously mentioned types, are a type of spiral bevel gear used for non-parallel, non-intersecting configurations. This design allows for components to be placed lower, allowing for more space in the sections above. Employing curved and angled teeth similar to those used in spiral bevel gears, hypoid gears are even more complex and, consequently, more difficult (and costly) to manufacture.

Hypoid gears look very much like a spiral bevel gear but they operate on shafts which do not intersect, which is the case with a spiral bevel gear. In the hypoid arrangement because the pinion is set on a different plane than the gear, the shafts are supported by the bearings on either end of the shaft.

3)     Non-intersecting and Non-Parallel gears.

a)     Worm Gears:  worm gear pairs are comprised of a worm wheel typically a cylindrical gear paired with a worm i.e., a screw-shaped gear. These gears are used to transmit motion and power between non-parallel, non-intersecting shafts. They offer large gear ratios and capabilities for substantial speed reduction while maintaining quiet and smooth operation.

Worm gears transmit power through right angles on non-intersecting shafts. Worm gears produce thrust load and are good for high shock load applications but offer very low efficiency in comparison to the other gears. Due to this low efficiency, they are often used in lower horsepower applications.

One distinction of worm gear pairs is that the worm can turn the worm wheel, but, depending on the angle of the worm, the worm wheel may not be able to turn the worm. This characteristic is employed in equipment requiring self-locking mechanisms. Some of the disadvantages of worm gears are the low transmission efficiency and the amount of friction generated between the worm wheel and worm gear which necessitates continuous lubrication.

4)     Rack and Pinion Gears

A rack and pinion is a pair of gears which convert rotational motion into linear motion and vice versa. A circular gear called “the pinion” engages teeth on a linear “gear” bar called “the rack”.

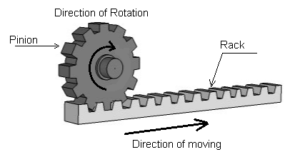
Rotational motion applied to the pinion will cause the rack to move to the side, up to the limit of its travel. The diameter of the gear determines the speed that the rack moves as the pinion turns.

A rack and pinion are commonly found in the steering mechanism of cars or other wheeled, steered vehicles. In a rack railway, the rotation of a pinion mounted on a locomotive or a railcar engages a rack between the rails and pulls a train along a steep slope, machine tools such as lathe machine, drilling machine, planning machine.

Rack and pinion gears are a pair of gears comprised of a gear rack and a cylindrical gear referred to as the pinion. The gear rack can be considered as a gear of infinite radius (i.e., a flat bar) and is constructed with straight teeth cut or inserted on the bar’s surface. Depending on the type of pinion gear with which it is mated, the gear rack’s teeth are either parallel (when mated with spur gears) or angled (when mated with helical gears). For either of these rack designs, rotational motion can be converted into linear motion or linear motion can be converted into rotational motion.

Some of the advantages of a rack and pinion gear pair are the simplicity of the design (and the low cost of manufacturing) and high load carrying capacities. Despite the advantages of this design, gears which employ this approach are also limited by it. For example, transmission cannot continue infinitely in one direction as motion is limited by the designated length of the gear rack. Additionally, rack and pinion gears tend to have a greater amount of backlash (i.e., additional space between mated gear teeth) and, consequently, the teeth experience a significant amount of friction and stress.

Some of the common applications of rack and pinion gear pairs include the steering system of automobiles, transfer systems, and weighing scales.

IV)           Gear train – simple and compound epicyclical gear train

A gear train is a mechanical system formed by mounting gears on a frame. When two or more gears mesh together to transmit power from one shaft to another such arrangement is called a gear set or a gear train.

Sometimes two or more gears are made to mesh with each other to transmit power from one shaft to another such a combination is called “gear train of the wheel”. Also, each gear is generally attached to a shaft often gears that are meshed together will be of different sizes in this case the smaller gear is referred to as the pinion and the larger one is simply referred to as the gear.

Following are the different types of gear trains:

1. Simple gear train
2. Compound gear trains
3. Reverted gear trains
4. Epicyclic gear trains

1. Simple Gear Trains

In these types of gear trains, the distance between the two wheels is great. The motion from one wheel to another is transmitted by providing one or more intermediate wheels as shown in the figure.

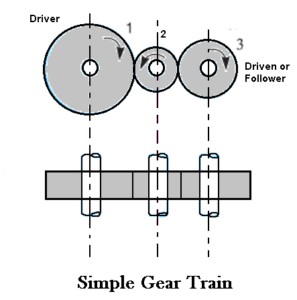
When the number of intermediate wheels is odd, the motion of driver and follower is like as shown in the figure. If the number of intermediate wheels is even the motion of the follower will be in the opposite direction of the driver as shown in the figure.

The speed ratio (or velocity ratio) of gear train is the ratio of the speed of the driver to the speed of the driven or follower and ratio of speeds of any pair of gears in mesh is the inverse of their number of teeth, therefore

Speed ratio: Speed of driver /speed of driven = NO. Of teeth on driven /No. Of teeth on driver.

Speed ratio = N1/N2 = T2 / T1

The train value may be noted that ratio of the speed of the driven or follower to the speed of the driver is known as train value of the gear train. Mathematically,

Train value: Speed of driven /speed of driver = NO. Of teeth on driver /No. Of teeth on driven.

Train value = N2 / N1 = T1 / T2

2. Compound Gear Train

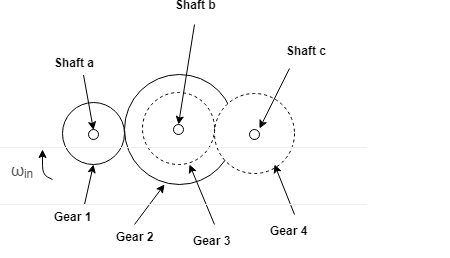
In compound gear train, each intermediate shaft has two wheels fixed to it. These wheels have the same speed. One wheel gears with the drier and the other wheel gears with the follower attached to the next shaft.

Speed ratio: Speed of first driver /speed of last driven = Product of the number of teeth on driven /product of the number of teeth on driver

Speed ratio = N1 / N6 = T2 X T4 X T6 / T1 X T3 X T5

Train value: Speed of last driver /speed of first driven = Product of the number of teeth on driver /product of the number of teeth on driven

3. Reverted Gear Trains

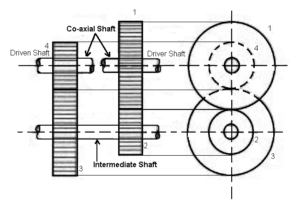
When the axes of the first and last wheels are co-axial the train is known as “reverted gear trains” as shown fig. Since the motion of the first and last wheel is alike, therefore a compound wheel is provided. Since the distance between the centres of the shaft 1 and 2 as well as 3 and 4 is the same.

Speed ratio: Speed of first driver /speed of last driven = Product of the number of teeth on driven /product of the number of teeth on drivers

Epicyclic gear train: the axes of the shaft, over which the gears are mounted, move relative to a fixed axis. A simple epicyclic or planetary gear train is shown the figure.

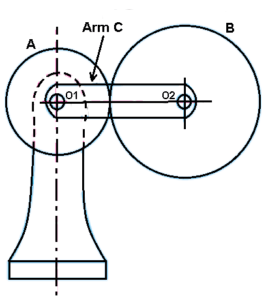
Here wheel A and arm C have a common axis at O1 about which they can rotate. The wheel B meshes with wheel A and has its axis on the arm at O2, about which the wheel B can rotate. If wheel A is fixed and the arm is rotated, the train becomes an “epicyclic gear train”.

Question 1) A compound gear consists of 4 gears A, B, C and D and they have 20, 30, 40 and 60 teeth respectively. A is fitted on the driver shaft, and D is fitted on the driven shaft, B and C are compound gears, B meshes with A, and C meshes with D. If A rotates at 180 rpm, find the rpm of D.?

Given:

TA= 20, TB= 30, TC= 40, TD= 60, N A=180 rpm

Find ND=?

Solution:

ND / NA = TA x TC / TB x TD

ND = NA x TA x TC / TB x TD

ND = 180 x 20 x 40 / 30 x 60

ND =  80 rpm

Question 2) Two gear wheels having 80 teeth and 30 teeth mesh with each other. If the smaller gear wheel runs at 480rpm, find the speed of the larger wheel.

Given:

Larger Gear wheel T1 = 80, N1=?

Smaller Gear Wheel T2= 30, N2= 480 rpm

Velocity ratio of gear drive

N2 / N1 = T1 / T2

N1 = N2 x T2  / T1

N1 = 480 x 30 / 80

= 180 rpm

Question 3) In a simple train of gears, A has 30 teeth, B has 40 teeth, C has 60 teeth and D has 40 teeth. If A makes 36 rpm, find the rpm of the gear C and D.

Given: TA= 30, TB= 40, TC= 60, TD= 40, NA=36 rpm

Find NC=?  ND=?

Solution =

NC / NA = TA / TC

NC = NA x TA / TC

= 36 x 30 / 60

= 18 rpm

ND / NA = TA / TD

ND = NA x TA / TD

= 36 x 30 / 40

= 27 rpm