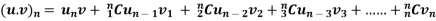Unit 1

Successive Differentiation and Mean Value Theorem

1.1 Definition and Symbol

It is the process of differentiating the given function simultaneously many times and  the result   obtained are  called successive  derivative.

Let 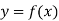be a differentiable function.

First derivative is denoted by

Second derivative is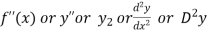  

Third derivative is

Similarly the nth derivative is

Successive differentiation-

The successive differential coefficients of y are denoted as follows-

……………….

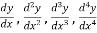The 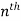differential coefficient is-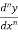

Other notations to denote n’th differential coefficients-

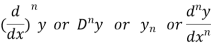
The process of applying differentiation again and again is called successive differentiation.

derivative of standard functions like 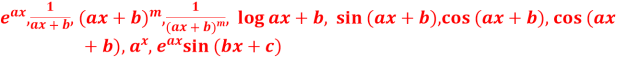and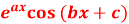

nth derivative of standard functions-

1. nth derivative of –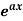

Suppose y = ,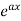

Differentiate with respect to x successively, we get

.

.

.

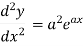
For n times differentiation, we get-

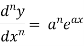
So we can say that its n’th derivative will be

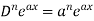
2. nth derivative of log(ax + b)-

Suppose y = log (ax + b)

Differentiate with respect to x successively, we get

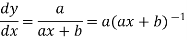
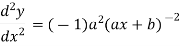
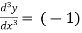(-2)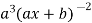

.

.

For n times differentiation, we get-

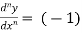(-2)…………….(-n + 1)

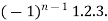=  …………….(n - 1)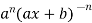

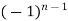= (n - 1)

So we can say that its n’th derivative will be

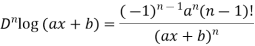
3. nth derivative of -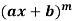

Suppose y =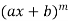

Differentiate with respect to x successively, we get

.

.

.

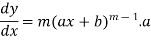
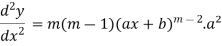
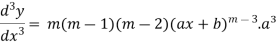
For n times differentiation, we get-

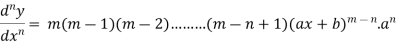
So we can say that its n’th derivative will be

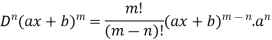
4.  nth derivative of sin(ax + b)-

Suppose y = sin(ax + b)

Differentiate with respect to x successively, we get

.

.

.

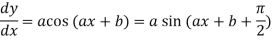
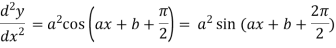
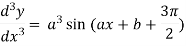
For n times differentiation, we get-

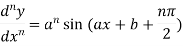
So we can say that its n’th derivative will be

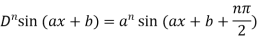
5. Nth derivative of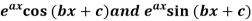

Let us consider the functions-

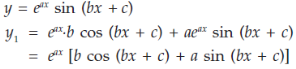
To rewrite this in the form of sin, put-

Diff. Again w.r.t.x, we get-

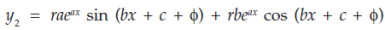
Substitute for a and b, we get-

…………………………………………………………………………

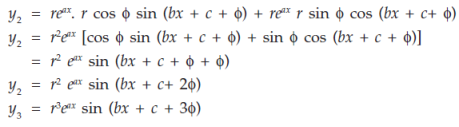
Similarly we get-

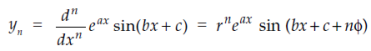
And

Similarly we can find the ‘n’ derivatives of such functions

Standard results-

1.

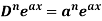
2.

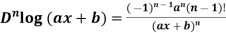
3.

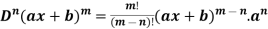
4.

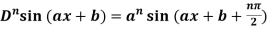
5.

6.

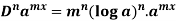
7.

Example:  If y = l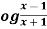 , then show that-

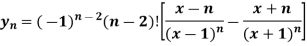
Sol. We have,

y =

Differentiate y with respect to x, we get

=

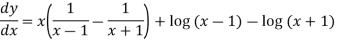
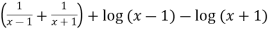
Again diff. (n – 1) times w.r .t x , we get-

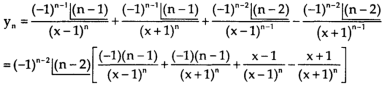
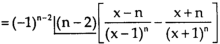
Order differential equation

N’th order differential equations can be solved as below-

Example: Find the 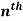derivative of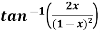

Sol. Here we have-

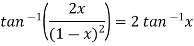
Suppose,   y =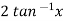

First derivative-

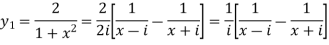
Here ,

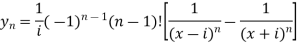
Let x =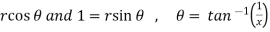

So that

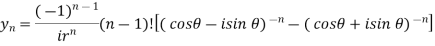
Which is the n’th derivative of the given function.

Example: Find cos x cos 2x cos 3x.

Sol.

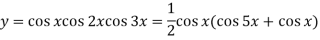
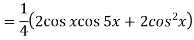
So that-

n’th derivative-

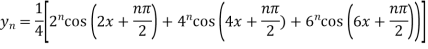
Key takeaways-

1.

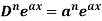
2.

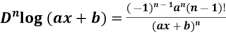
3.

4.

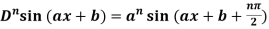
5.

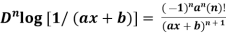
6.

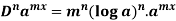
7.

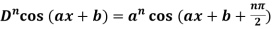
derivatives of algebraic functions, derivatives of function belongs to polar form

Example: Find the 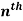derivative of the following function-

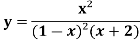
Sol.  Partial fraction of the function y after splitting-

Suppose x – 1 = z, then

=

=

=

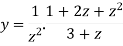
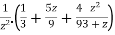
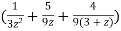
Here we can find its n’th derivative-

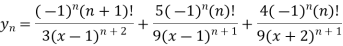
Example: Find 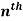derivative of the given function:

y =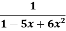

Sol.   We are given-

y =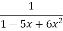

Factorize the denominator-

y =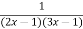

=

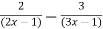
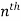derivative will be-

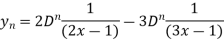
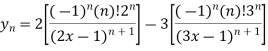
Which is the derivative of the given function.

Example: Find if

Sol.

Here we have-

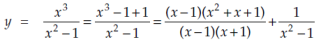
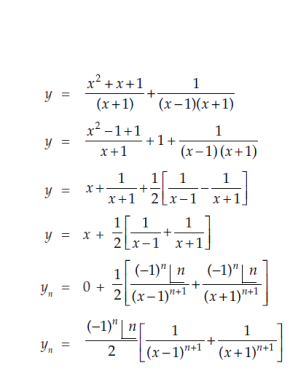
At x = 0,

When n is odd-

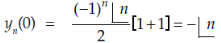
When n is even

1.4 Statements of Leibnitz’s Theorem (without proof)

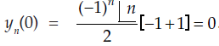
If u and v are the function of x  such  that  their nth  derivative exists, then the nth derivative of  their product will  be

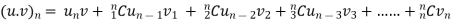
derivative of product of two functions by Leibnitz theorem

Example-1 If   y 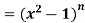 , then prove that-

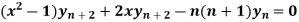
Sol. Here it is given that-

On differentiating-

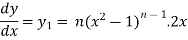
Or

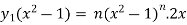
= ny.2x

Differentiate again with respect to x, we get-

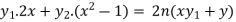
Or

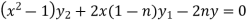   …………………. (1)

Differentiate each term of (1) by using Leibnitz’s theorem, we get-

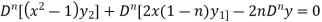
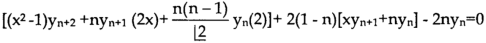
Therefore we get-

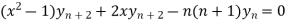
Hence proved.

Example-2: If 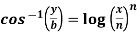, then prove that-

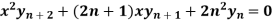
Sol. Here we have-

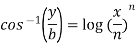
Or

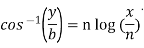
Or

y = b cos[ n log(x/n)]

On differentiating, we get-

Which becomes-

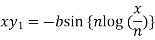
Differentiate again both sides with respect to x, we get-

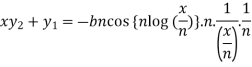
It becomes-

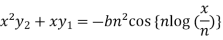
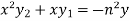
       ……………….. (1)

Differentiate each term n times with respect to x, we get-

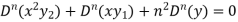
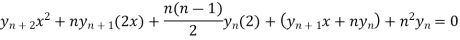
Which is-

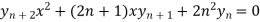hence proved,

Example-3: If y = 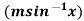, then prove that-

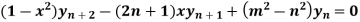
Sol. It is given that-    y =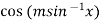

First derivative –

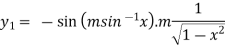
It becomes-

= 

=

=

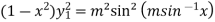
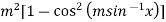
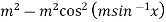
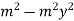
Becomes-

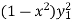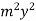+ - = 0

Om differentiating again we get-

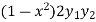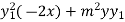+ = 0

Or

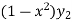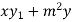+ = 0

Differentiate n times by using Leibnitz’s theorem, we get-

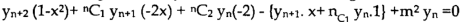
So that

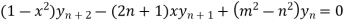
Hence proved.

Example-4: Find  the nth derivative of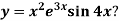  

Sol.

Let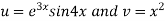

Also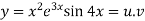

By Leibnitz’s theorem

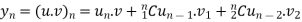
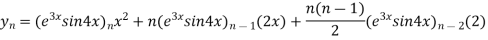
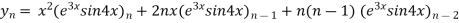    …(i)

Here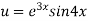 

Differentiating with  respect  to  x, we get

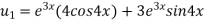
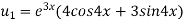
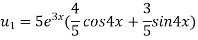
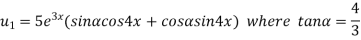
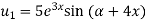
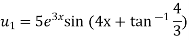
Again  differentiating  with respect to x, we get

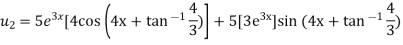
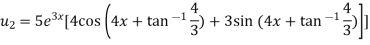
Similarly  the  nth derivative will be

From  (i) and (ii) we have,

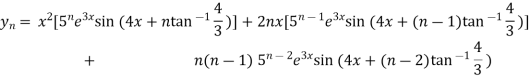
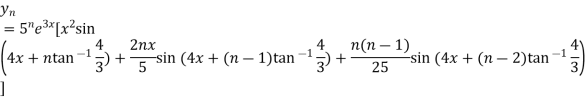
Example-5: If 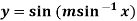,     then show that

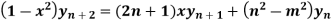
Sol.

Also, find 

Here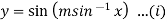

Differentiating with respect to x, we get

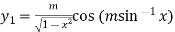   …(ii)

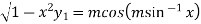
Squaring   both  side  we get

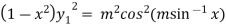
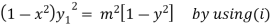
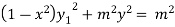   …(iii)

Again differentiating with  respect to  x ,we get

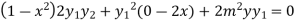
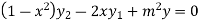
Using Leibnitz’s  theorem  we  get

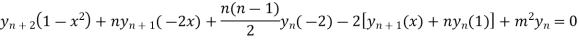
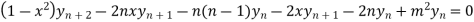
        …(iv)

Putting x=0  in equation (i),(ii) and (iii)  we get

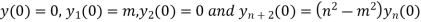
Putting  n=1,2,3,4….

………………

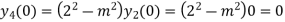
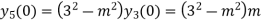
Hence   

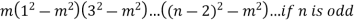
Example-6: If 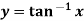then show that 

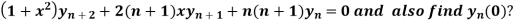
Sol.

Given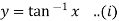 

Differentiating both side  with  respect to  x.

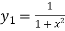          …..(ii)

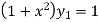
Again differentiating with  respect to  x, we get

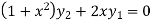     …(iii)          

By  Leibnitz’s theorem

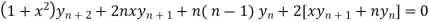
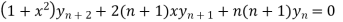…(iv)

Putting x=0 in equation  (i),(ii),(iii) and (iv) we  get

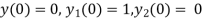
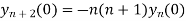
Putting n=1,2,3,4… so  we get

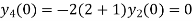
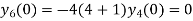
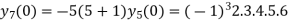
Hence we  have

Key takeaways-

Formation of higher order differential equations for the given functions

1.6 Rolle’s Mean Value Theorem

Statement

Suppose f(x) is a function defined on [a , b] and it satisfies the following conditions

1. f(x) is continuous in [a , b]

2. f(x) is differentiable in (a , b)

3. f(a) = f(b)

Then there exists atleast a point c ϵ (a , b) , where a<b , such that f’(c) = 0

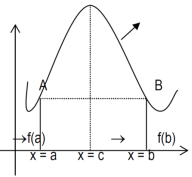
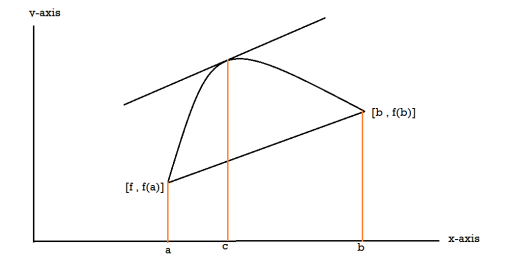
Proof: suppose y = f(x) is a function and A(a , f(a)) , B(b , f(b)) be two points on the curve f(x) and a,b are two end points. Now conditions for Rolle’s theorem-

1.f(x) is a continuous function in[a , b] , from the figure without breaks in between  A&B on y = f(x).

2. f(x) is differentiable in (a , b), because joining A and B we get a line AB.

Slope of the line AB=0 then a point C at P also a tangent at P, or Q,R,S is parallel to x –axis.

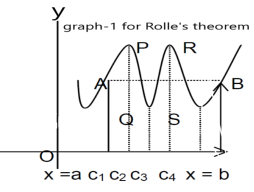
Slope of the tangent at P or Q,R,S , will be 0 ,even the curve y = f(x) decreases or increases, that means f(x) is constant.

Derivative of f(x),

f’(c) = 0

That’s why,     f’(c) = 0

3. The slope of the line AB is equal to zero, that means the line AB is parallel to x-axis.

So that,       f(a) = f(b)

Example 1

Verify Rolle’s theorem for the function f(x) = x2 for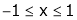

Solution:

Here f(x) = x2;

i)      Since f(x) is algebraic polynomial which is continuous in [-1, 1]

Ii)    Consider f(x) = x2

Diff. w.r.t. x we get

f'(x) = 2x

Clearly f’(x) exists in (-1, 1) and does not becomes infinite.

Iii)  Clearly

f(-1) = (-1)2 = 1

f(1) = (1)2 = 1

f(-1) = f(1).

Hence by Rolle ’s Theorem, there exist 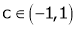such that

f’(c) = 0

i.e. 2c = 0

c = 0

Thus 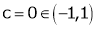such that

f'(c) = 0

Hence Rolle’s Theorem is verified.

Example 2

Verify Rolle’s Theorem for the function f(x) = ex(sin x – cos x) in

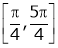
Solution:

Here f(x) = ex(sin x – cos x);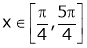

i)      Ex is an exponential function continuous for every 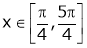also sin x and cos x are Trigonometric functions Hence (sin x – cos x) is continuous in and Hence ex(sin x – cos x) is continuous in .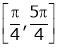

Ii)    Consider

f(x) = ex(sin x – cos x)

Diff. w.r.t. x we get

f’(x) = ex(cos x + sin x) + ex(sin x + cos x)

= ex[2sin x]

Clearly f’(x) is exist for each 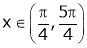& f’(x) is not infinite.

Hence f(x) is differentiable in .

Iii)  Consider

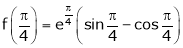
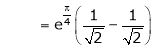
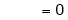
Also,

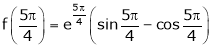
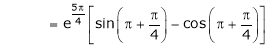
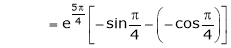
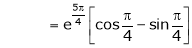
Thus

Hence all the conditions of Rolle’s theorem are satisfied, so there exist 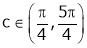such, that

i.e.

i.e. sin c = 0

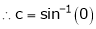
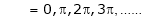
But

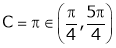
Hence Rolle’s theorem is verified.

Example-3

Verify whether Rolle’s theorem is applicable or not for

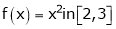
Solution:

Here f(x) = x2;

i)      X2 is an algebraic polynomial hence it is continuous in [2, 3]

Ii)    Consider

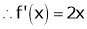
F’(x) exists for each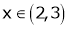

Iii)  Consider

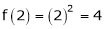
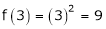
Thus .

Thus all conditions of Rolle’s theorem are not satisfied Hence Rolle’s theorem is not applicable for f(x) = x2 in [2, 3]

Example-4:

Example: Verify Rolle’s theorem for the given functions below-

1.  f(x) = x³ - 6x²+11x-6  in the interval [1,3]

2. f(x) = x²-4x+8  in the interval [1,3]

Sol. (1)

As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]

Also, f(1) = f(3) = 0

Now we find f’(x) = 0

3x² - 12x +11 = 0

We get, x = 2+ 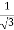and 2 -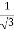

Hence both of them lie in (1,3).

Hence the theorem holds good for the given function in interval [1,3]

(2) As we know that every polynomial is continuous and differentiable for all points, so that the given function is continuous and differentiable in the interval [1,3]

Also,  f(1) = 1 -4 +8 = 5 and f(3) = 9 – 12 + 8 = 5

Hence f(1) = f(3)

Now the first derivative of the function,

f’(x) = 0

2x – 4 = 0 , gives

X = 2

We can see that 1<2<3, hence there exists 2 between 1 and 3. And f’(2) = 0.

This means that the Rolle’s theorem holds good for the given function and given interval.             

Key takeaways-

Suppose f(x) is a function defined on [a , b] and it satisfies the following conditions

1. f(x) is continuous in [a , b]

2. f(x) is differentiable in (a , b)

3. f(a) = f(b)

1.7 Lagrange’sMean Value Theorem

Statement

Suppose that f(x) be a function of x such that,

1. If it is continuous in [a , b]

2. If it is differentiable in (a , b)

Then there atleast exists a value cϵ (a , b)

f’(c) =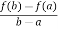

Proof:

Lets define a function g(x),

g(x) = f(x) – Ax  ………………..(1)

Here A is a constant which is to be determined,

So that,  g(a) = g(b)

Now,

g(a) = f(a) – Aa

g(b) = f(b) – Ab

So,

g(a) = g(b),

f(a) – Aa = f(b) – Ab ,

Which gives,

A = 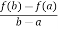    …………………..(2)

As right hand side of eq.(1) is continuous in [a,b] , so that g(x) is continuous.

And right hand side of eq.(1) is differential in (a,b) , so that g(x) is differentiable in (a,b).

And g(a) = g(b) , because of the choice of A.

Hence g(x) satisfies all the conditions of Rolle’s theorem.

So that,

There exists a value c  such that a<c<b at which g’(c) = 0

Now, differentiate eq. (1) with respect to x, we get

g’(x) = f’(x) – A

Here we know that, x = c,

g’(c) = f’(c) – A

As g’(c) = 0, then

f’(c) – A =0

So that,, f’(c) = A,

From equation (2) , we get

f’(c) = 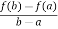                                            hence proved.

Example-1:

Verify the Lagrange’s mean value theorem for

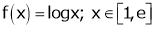
Solution:

Here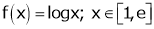

i)      Clearly f(x) = log x is logarithmic function. Hence it is continuous in [1, e]

Ii)    Consider f(x) = log x.

Diff. w.r.t. x we get,

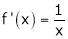
Clearly f’(x) exists for each value of 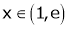& is finite.

Hence all conditions of LMVT are satisfied Hence at least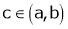

Such that

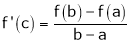
i.e.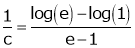

i.e.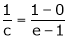

i.e.

i.e.

Since e = 2.7183

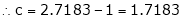
Clearly c = 1.7183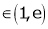

Hence LMVT is verified.

Example-2:

Verify mean value theorem for f(x) = tan-1x in [0, 1]

Solution:

Here ;

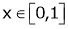
i)      Clearly 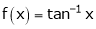is an inverse trigonometric function and hence it is continuous in [0, 1]

Ii)    Consider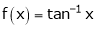

Diff. w.r.t. x we get,

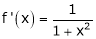
Clearly f’(x) is continuous and differentiable in (0, 1) & is finite

Hence all conditions of LMVT are satisfied, Thus there exist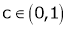

Such that

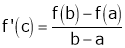
i.e.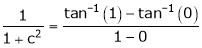

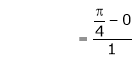
i.e.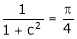

i.e.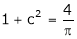

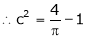
i.e.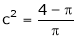

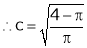
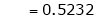
Clearly

Hence LMVT is verified.

Example-4;

Verify Lagrange’s mean value theorem for f(x) = (x-1)(x-2)(x-3) in [0,4].

Sol. As we see that the given function is a polynomial and we know that the polynomial is continuous in [0,4] and differentiable in (0,4).

f(x) = (x-1)(x-2)(x-3)

f(x) =  x-6x²+11x-6

Now at x = 0, we get

f(0) = -6  and

At x = 4, we get.

f(4) = 6

Diff. The function w.r.t.x , we get

f’(x) = 3x²-6x+11

Suppose x = c, we get

f’(c) = 3c²-6c+11

By Lagrange’s mean value theorem,

f’(c) = 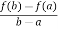   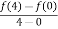 =  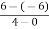   =   = 3                                                                                                                        

Now we get,

3c²-6c+11 = 3

3c²-6c+8 = 0

On solving the quadratic equation, we get

C = 2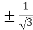

Here we see that the value of c lies between 0 and 4

Therefore the given function is verified.

Meaning of sign of Derivative:

Let f(x) satisfied LMVT in [a, b]

Let x1 and x2 be any two points laying (a, b) such that x1< x2

Hence by LMVT, 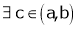such that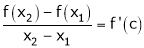

i.e. 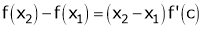      … (1)

Cast I:

If 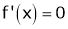then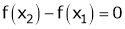

i.e.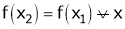

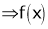is constant function

Case II:

If 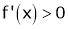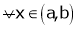then from equation (1)

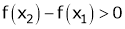
i.e.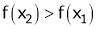

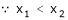means x2 - x1> 0 and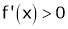

Thus for x2> x1

Thus f(x) is increasing function is (a, b)

Case III:

If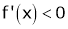

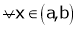
Then from equation (1)

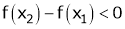
i.e.  

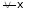
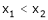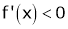Since and then 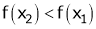hence f(x) is strictly decreasing function.

Example-5:

Prove that

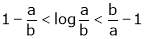
And hence show that

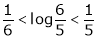
Solution:

Let

; 

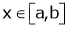
i)      Clearly is a logarithmic function and hence it is continuous also

Ii)    Consider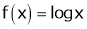

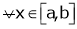
Diff. w.r.t. x we get,

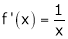
Clearly f’(x) exist and finite in (a, b) Hence f(x) is continuous and differentiable in (a, b). Hence by LMVT

Such that

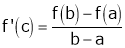
i.e.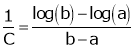

i.e.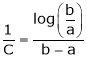

Since

a < c < b

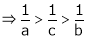
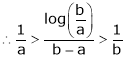
i.e.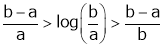

i.e.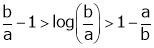

i.e.

i.e.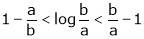

Hence the result

Now put a = 5, b = 6 we get

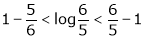
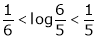
Hence the result

Example-6:

Prove that 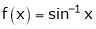, 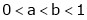use mean value theorem to prove that,

Hence show that

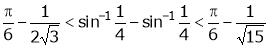
Solution:

i)      Let f(x) = sin-1x; 

Ii)    Clearly f(x) is inverse trigonometric function and hence it is continuous in [a, b]

Iii)  Consider f(x) = sin-1x

Diff. w.r.t. x we get,

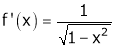
Clearly f’(x) is finite and existsfor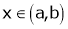. Hence by LMVT, 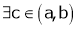such that

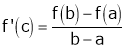
i.e.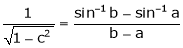

Since a < c < b

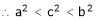
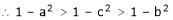
i.e.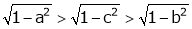

i.e.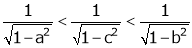

i.e.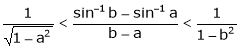

i.e.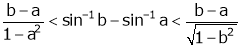

Hence the result

Put 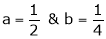we get

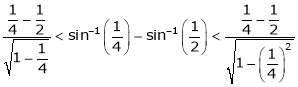
i.e.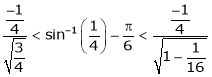

i.e.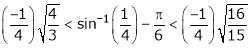

i.e.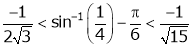

i.e.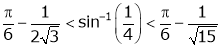

Hence the result

Key takeaways-

Suppose that f(x) be a function of x such that,

1. If it is continuous in [a , b]

2. If it is differentiable in (a , b)

Then there atleast exists a value cϵ (a , b)

f’(c) =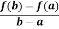

1.8 Cauchy’s Mean Value Theorem

Statement:

Suppose we have two functions f(x) and g(x) of x, such that,

1. Both functions are continuous in [a,b]

2. Both functions are differentiable in (a,b)

3. g’(x) ≠ 0 for any x ϵ (a,b)

These three exists atleast , x = c ϵ (a,b) , at which

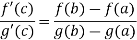
Proof: suppose ,we define a functions,

h(x) = f(x) – A.g(x) …………………….(1)

So that h(a) = h(b) and A is a constant to be determined.

Now ,

h(a) = f(a) – Ag(a)

h(b) = f(b) – A.g(b)

So that,

f(a) – Ag(a) = f(b) – A.g(b) , which gives

A = 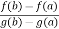    …………………………….(2)

Now, h(x) is continuous in [a,b] as RHS of eq. (1) is continuous in [a,b] and h(x) is diff. In (a,b) as RHS of eq. (1) is diff. In (a,b)

Also,

h(a) = h(b)

Therefore all the conditions of Rolle’s theorem are satistfied then there exists a value  x = cϵ (a,b)

So that h’(c) = 0

Differentiate eq.(1) w.r.t. x , we get

h’(x) = f’(x) – A.g’(x)

At x = c

h’(c) = f’(c) – A.g’(c)

0 = f’(c) – A.g’(c)

A =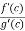

So that, we get

where a<c<b

Hence the Cauchy’s mean value theorem is proved.

Example-7:

Verify Cauchy mean value theorems for 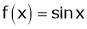&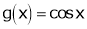in

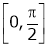
Solution:

Let &;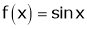

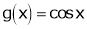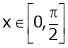
i)      Clearly f(x) and g(x) both are trigonometric functions. Hence continuous in

Ii)    Since &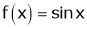

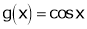
Diff. w.r.t. x we get,

&

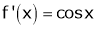Clearly both f’(x) and g’(x) exist & finite in 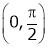. Hence f(x) and g(x) is derivable in 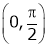and

Iii)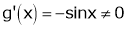   

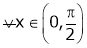
Hence by Cauchy mean value theorem, there exist at least 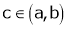such that

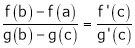
i.e.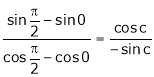

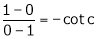
i.e. 1 = cot c

i.e.

Clearly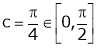

Hence Cauchy mean value theorem is verified.

Example-8:

Considering the functions ex and e-x, show that c is arithmetic mean of a & b.

Solution:

i)      Clearly f(x) and g(x) are exponential functions Hence they are continuous in [a, b].

Ii)    Consider &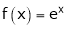

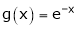
Diff. w.r.t. x we get

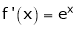and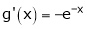

Clearly f(x) and g(x) are derivable in (a, b)

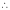By Cauchy’s mean value theorem such that

i.e.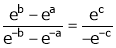

i.e.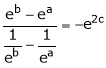

i.e.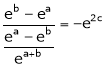

i.e.

i.e.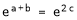

i.e.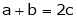

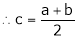
Thus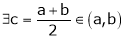

i.e. c is arithmetic mean of a & b.

Hence the result

Example-9

Show that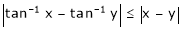

Prove that if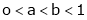

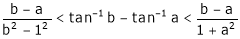and Hence show that

Verify Cauchy’s mean value theorem for the function x2 and x4 in [a, b] where a, b > 0

If for then prove that,

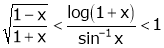
[Hint:, ]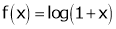

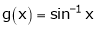Example-10:

Verify Cauchy’s mean value theorem for the function f(x) = x⁴ and g(x) = x² in the interval [1,2]

Sol. We are given, f(x) = x⁴ and g(x) = x

Derivative of these fucntions ,

f’(x) = 4x³ and g’(x) = 2x

Put these values in Cauchy’s formula, we get

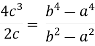
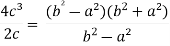
2c² =

c² =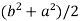

c =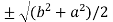

Now put the values of a = 1 and b = 2 ,we get

c = 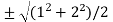= =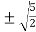 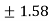(approx..)

Hence the Cauchy’s theorem is verified.

Key takeaways-

Suppose we have two functions f(x) and g(x) of x, such that,

1. Both functions are continuous in [a,b]

2. Both functions are differentiable in (a,b)

3. g’(x) ≠ 0 for any x ϵ (a,b)

These three exists atleast , x = c ϵ (a,b) , at which

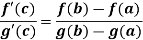
References

1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.

2. N.P. Bali and Manish Goyal, A textbook of Engineering Mathematics, Laxmi Publications.

3. Higher engineering mathematic, Dr. B.S. Grewal, Khanna publishers

4. HK dass, engineering mathematics.