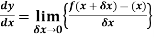Unit-2
Expansion of Functions and Indeterminate forms
Maclaurin’s series-
+ …….
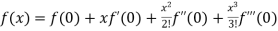Which is called Maclaurin’s theorem.
Note – if we put h = x - a then there will be the expansion of F(x) in powers of (x – a)
We get-
+ …….
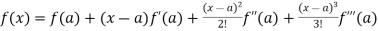Expansion of functions using standard expansions-
Example: By using Maclaurin’s series expand tan x.
Sol.
Let-
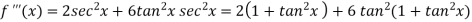
Put these values in Maclaurin’s series we get-
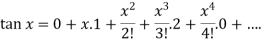
Example: Expand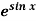 
by using Maclaurin’s series.
Sol.
Let
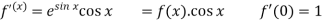
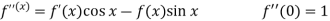
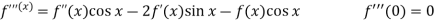
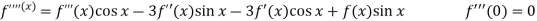
Put these values in Maclaurin’s series-
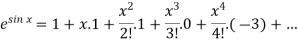
Or
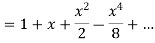
Key takeaways-
Maclaurin’s series-
+ …….
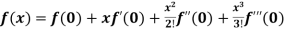Formulas
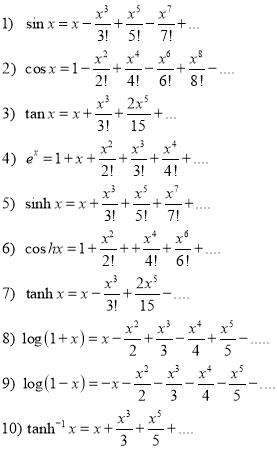
Problem 1:
Prove that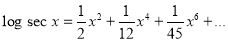 
Solution:
Let 
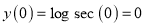
Differentiate with respect to x,
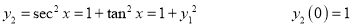
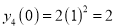
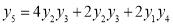
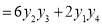
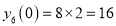
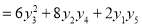
Hence by Maclaurin’s Series,
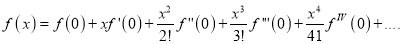
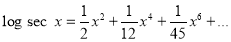
Problem 2:
Show that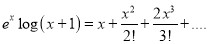 
Solution:
Let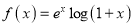 
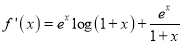
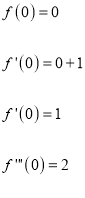
By Maclaurin’s Series,
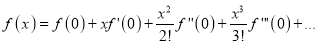
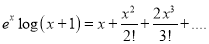
Method of using standard expansions:
Problem 1: Expand by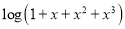 
upto
.
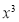Solution:
We have,
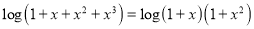
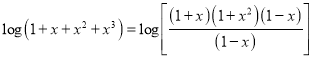
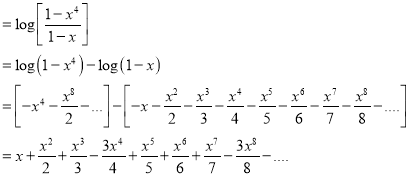
Problem 2: Show that 
Solution:
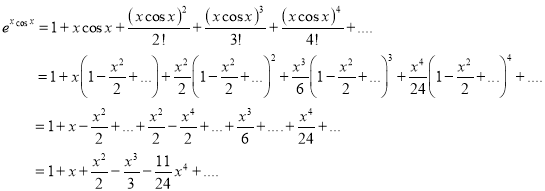
Problem 3: Show that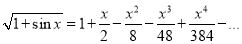
Solution:
Given that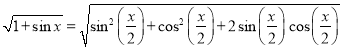 
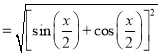
Problem 4: Expand in power of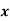 
, 
. Hence prove that 
Solution:
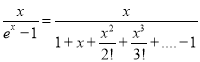
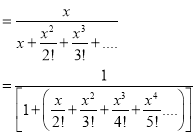
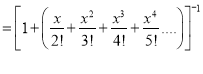
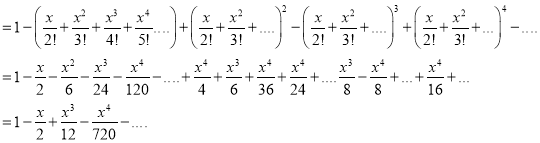
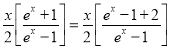
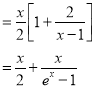
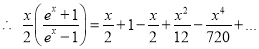
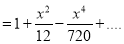
Differentiation from first principal-
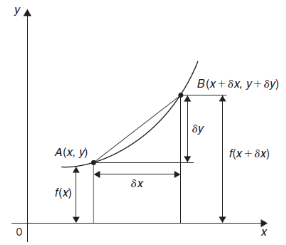
A and B are the two point on a curve representing small increment in the x and y directions respectively.
Gradient of chord-
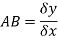
However-
Hence-
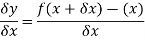
Here 
which approaches to 0,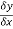 
approches a limiting value of the gradient of the chord approaches the gradient of the tangent A.
When determining the gradient of a tangent to a curve there are two notations used. The gradient of the curve at A can either be written as,
Where
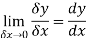
Or we can write it as-
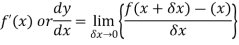
Example: Differentiate the function f(x) =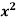 
by using the first principal method.
Sol.
We know that-
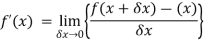
Here
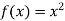
Substituting (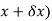
for x gives-
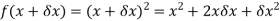
Hence-
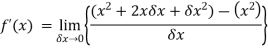
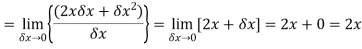
Differentiation of common functions-
f(x) | Dy/dx |
 |  |
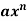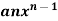Sin ax | a cos ax |
Cos ax | -a sin ax |
 |  |
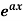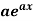Log ax | 1/x |
Example: Find the derivative of y = 3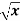 
Sol.
We can write the given function y = 3 
as-
y = 3 
So that-
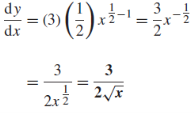
Example: Differentiate with respect to x-
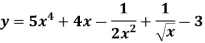
Sol.
The given function can be written in the form
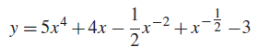
Now-
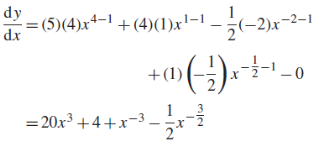
Differentiation of a product-
When y = uv and u, v are both function of x-
Then
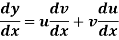
Differentiation of a quitient-
When y = u/v and u,v are the functions of x-
Then-
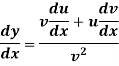
Example: Differential the following function-
Sol.
We know that-
Key takeaways-
Integration-
The general solution of integrals of the form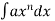 
where a and n are constants is given by-
For example:
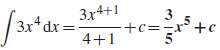
Some important standard integrals-
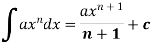
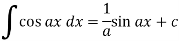
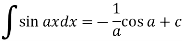
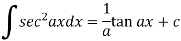
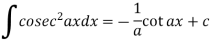
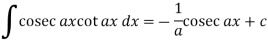
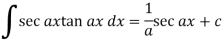
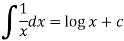
Example: Determine-
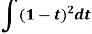
Sol.
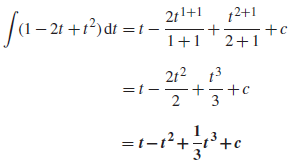
Example: Determine-
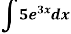
Sol.
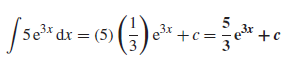
Example: Determine-
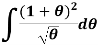
Sol.
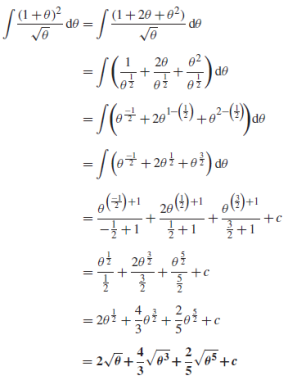
Key takeaways-
1.
2.
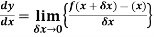
3. 
4. 
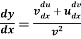
2.5 Statement of Taylor’s series (without proof), expansion of functions 
about any point
Taylor’s Series Expansion:-
a) The expansion of f(x+h) in ascending power of x is
b) The expansion of f(x+h) in ascending power of h is
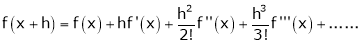
c) The expansion of f(x) in ascending powers of (x-a) is,
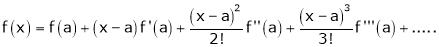
Using the above series expansion we get series expansion of f(x+h) or f(x).
Expansion of functions using standard expansions-
Example-1: Expand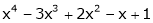 
in power of (x – 3)
Solution:
Let 
Here a = 3
Now by Taylor’s series expansion,
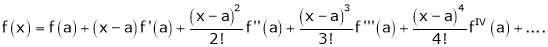… (1)
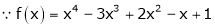
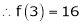
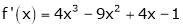
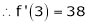
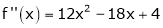
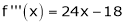
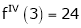
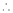equation (1) becomes.
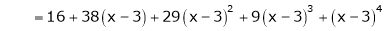
Example-2:
Using Taylors series method expand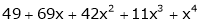 
in powers of (x + 2)
Solution:
Here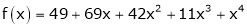 
a = -2
By Taylors series,
… (1)
Since
, 
, …..
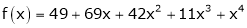
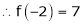
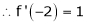
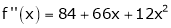
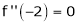
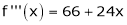
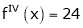
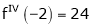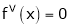Thus equation (1) becomes
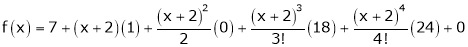
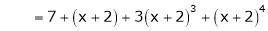
Example-3:
Expand 
in ascending powers of x.
Solution:
Here
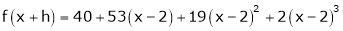
i.e.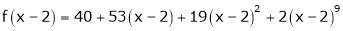 
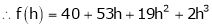
Here h = -2
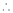By Taylors series,
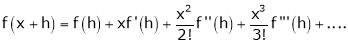… (1)
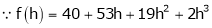
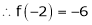
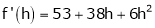
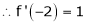
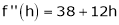
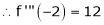
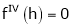
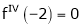
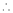equation (1) becomes,
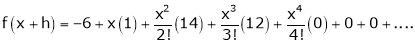
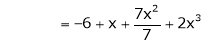
Thus
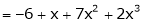
Example-4:
Expand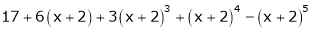 
in powers of x using Taylor’s theorem,
Solution:
Here
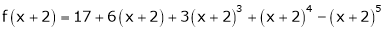
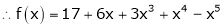
i.e.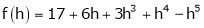 
Here
h = 2
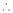By Taylors series
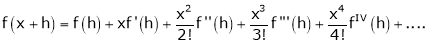… (1)
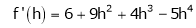
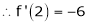
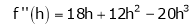
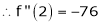
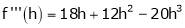
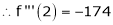
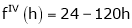
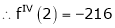
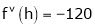
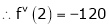
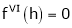
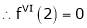
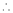By equation (1)
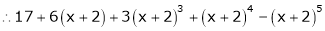
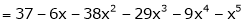
Key takeaways-
Taylor’s Series Expansion:-
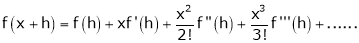
2.6 Indeterminate forms of the type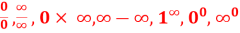 
by L’Hospital’s rule
Let we have two functions f(x) and g(x) and-
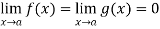
Then-
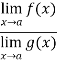
Is an expression of the form 
In that case we can say that f(x)/g(x) is an indeterminate for of the type 
at x = a.
Now, Let we have two functions f(x) and g(x) and-
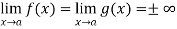
Then-
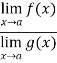
Is an expression of the form 
, in that case we can say that f(x)/g(x) is an indeterminate for of the type 
at x = a.
Some other indeterminate forms are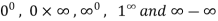 
L’Hospital’s rule for 
form-
Working steps-
1. Check that the limits f(x)/g(x) is an indeterminate form of type 
.
(Note- we can not apply L’Hospital rule if it is not in indeterminate form)
2. Differentiate f and g separately.
3. Find the limits of the derivatives .if the limit is finite ,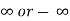
then it is equal to the limit of f(x)/g(x).
Example-1: Evaluate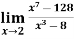 
Sol. Here we notice that it is an indeterminate form of 
.
So that , we can apply L’Hospital rule-
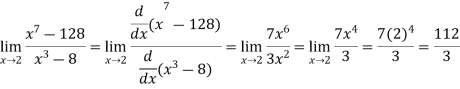
Example-2: Evaluate 
.
Sol. Let f(x) =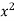 
and g(x) = 
.
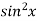Here we see that this is the indeterminate form of 0/0 at x = 0.
Now by using L’Hospital rule, we get-
= 
= 
= 
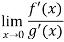
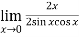
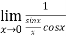
= 1
Note- Suppose we get an indeterminate form even after finding first derivative, then in that case , we use the other form of L’Hospital’s rule.
If we have f(x) and g(x) are two functions such that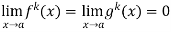 
.
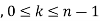If 
exist or (∞ , -∞), then
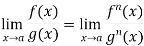
Example-3: Evaluate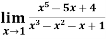 
Sol. Let f(x) =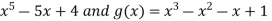 
, then
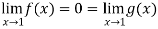
And
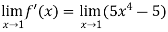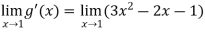= 0
= 0
But if we use L’Hospital rule again, then we get-
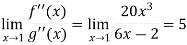
Example-4: Evaluate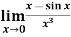 
Sol. We can see that this is an indeterminate form of type 0/0.
Apply L’Hospital’s rule, we get
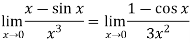
But this is again an indeterminate form, so that we will again apply L’Hospital’s rule-
We get
= 
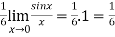
L’Hospital’s rule for 
form-
Let f and g are two differentiable functions on an open interval containing x = a, except possibly at x = a and that
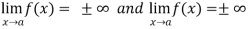
If 
has a finite limit, or if it is 
, then
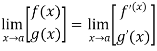
Theorem- If we have f(x) and g(x) are two functions such that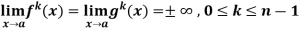 
.
If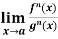 
exist or (∞ , -∞), then
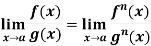
Example-5: Find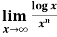 
, n>0.
Sol. Let f(x) = log x and g(x) =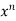 
These two functions satisfied the theorem that we have discussed above-
So that,
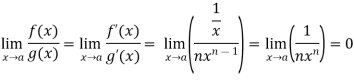
Example-6: Evaluate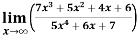 
Sol. Apply L’Hospital rule as we can see that this is the form of 
= 
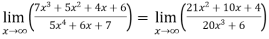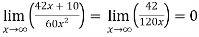
Note- In some cases like above example, we can not apply L’Hospital’s rule.
Other types of indeterminate forms-
Example-7: Evaluate 
Sol. Here we find that-
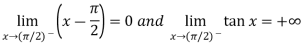
So that this limit is the form of 0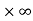
.
Now,
Change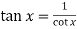 
to obtain the limit-
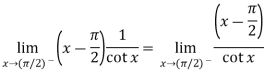
Now this is the form of 0/0,
Apply L’Hospital’s rule-
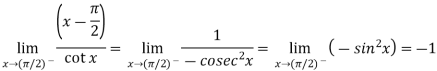
Key takeaways-
If we have f(x) and g(x) are two functions such that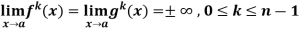 
.
If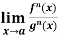 
exist or (∞ , -∞), then
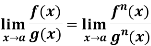
References
1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.
2. N.P. Bali and Manish Goyal, A textbook of Engineering Mathematics, Laxmi Publications.
3. Higher engineering mathematic, Dr. B.S. Grewal, Khanna publishers
4. HK dass, engineering mathematics.
