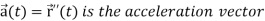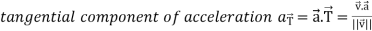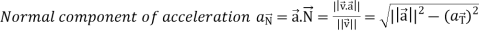Unit 6
Vector Differential Calculus
Vector function-
Suppose 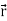 be a function of a scalar variable t, then-
be a function of a scalar variable t, then-
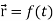
Here vector 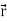 varies corresponding to the variation of a scalar variable t that its length and direction be known as value of t is given.
varies corresponding to the variation of a scalar variable t that its length and direction be known as value of t is given.
Any vector 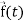 can be expressed as-
can be expressed as-
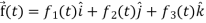
Here 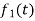 ,
, 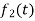 ,
, 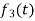 are the scalar functions of t.
are the scalar functions of t.
Differentiation of a vector-

We can denote it as- 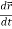
Similarly 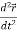 is the second order derivative of
is the second order derivative of 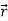
Note- 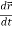 gives the velocity and
gives the velocity and 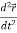 gives acceleration.
gives acceleration.
Note-
1. Velocity = 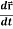
2. Acceleration = 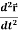
The derivative of the velocity vector V(t) is called acceleration A(t), and it is given as-
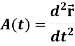
Rules for differentiation-
1. 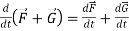
2. 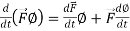
3. 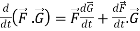
4. 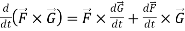
5. 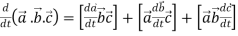
Example-1: A particle moves along the curve 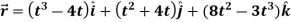 , here ‘t’ is the time. Find its velocity and acceleration at t = 2.
, here ‘t’ is the time. Find its velocity and acceleration at t = 2.
Sol. Here we have-
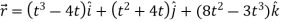
Then, velocity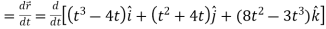
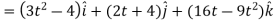
Velocity at t = 2,
= 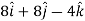
Acceleration = 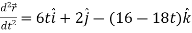
Acceleration at t = 2,
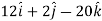
Example-2: If 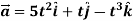 and
and 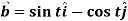 then find-
then find-
1. 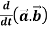
2. 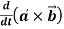
Sol. 1. We know that-
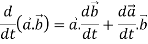
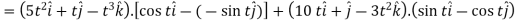

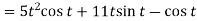
2.

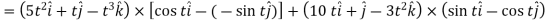
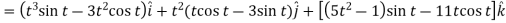
Example-3: A particle is moving along the curve x = 4 cos t, y = 4 sin t, z = 6t. Then find the velocity and acceleration at time t = 0 and t = π/2.
And find the magnitudes of the velocity and acceleration at time t.
Sol. Suppose 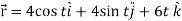
Now,
At t = 0 | 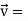 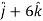 |
At t = π/2 | 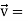 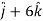 |
At t = 0 | |v|= 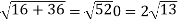 |
At t = π/2 | |v|= 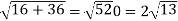 |
Again acceleration-
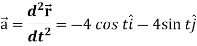
Now-
At t = 0 | 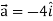 |
At t = π/2 | 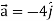 |
At t = 0 | |a|= 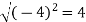 |
At t = π/2 | |a|= 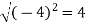 |
Scalar point function-
If for each point P of a region R, there corresponds a scalar denoted by f(P), in that case f is called scalar point function of the region R.
Note-
Scalar field- this is a region in space such that for every point P in this region, the scalar function ‘f’ associates a scalar f(P).
Vector point function-
If for each point P of a region R, then there corresponds a vector 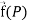 then
then 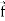 is called a vector point function for the region R.
is called a vector point function for the region R.
Vector field-
Vector filed is a reason in space such that with every point P in the region, the vector function  associates a vector
associates a vector 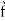 (P).
(P).
Note-
Del operator-
The del operated is defined as-
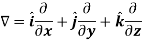
Example: show that 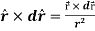 where
where 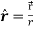
Sol. Here it is given-
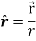
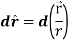
= 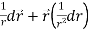
Therefore-
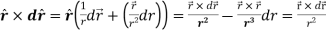 Note-
Note-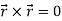
Hence proved
Key takeaways-
- Any vector
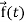 can be expressed as-
can be expressed as-
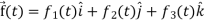
Here 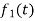 ,
, 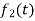 ,
, 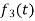 are the scalar functions of t.
are the scalar functions of t.
1. Velocity = 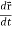
2. Acceleration = 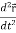
3. Scalar field- this is a region in space such that for every point P in this region, the scalar function ‘f’ associates a scalar f(P).
4. Vector field-
Vector filed is a reason in space such that with every point P in the region, the vector function 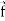 associates a vector
associates a vector 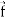 (P).
(P).
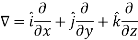
Tangential and normal accelerations-
It is very important to understand that the magnitude of acceleration is not always the rate of change of |V|.
Suppose 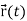 be the vector-valued function which denotes the position of any object as a function of time.
be the vector-valued function which denotes the position of any object as a function of time.
Then
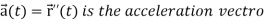
Then the tangential and normal component of acceleration are given as below-
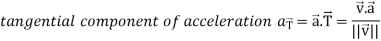

Example: A object move in the path 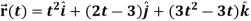 where t is the time in seconds and distance is measured in feets.
where t is the time in seconds and distance is measured in feets.
Then find 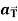 and
and 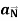 as functions of t.
as functions of t.
Sol.
We know that-
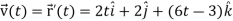
And
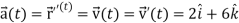
Now we will use-
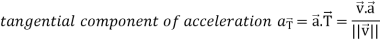
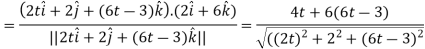

And now-
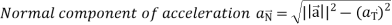
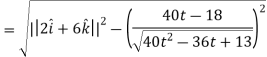
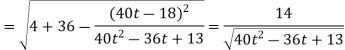
Key takeaways-
The vector differential operator is written as-
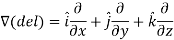
Gradient
Suppose f(x, y, z) be the scalar function and it is continuously differentiable then the vector-
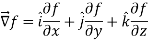
Is called gradient of f and we can write is as grad f.
So that-
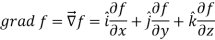
Here 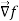 is a vector which has three components
is a vector which has three components 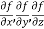
Properties of gradient-
Property-1: 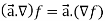
Proof:
First we will take left hand side
L.H.S = 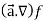
= 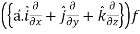
= 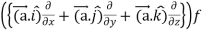
= 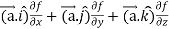
Now taking R.H.S,
R.H.S. = 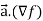
= 
= 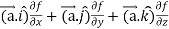
Here- L.H.S. = R.H.S.
Hence proved.
Property-2: Gradient of a constant (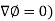
Proof:
Suppose 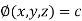
Then 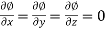
We know that the gradient-
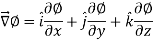
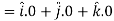
= 0
Property-3: Gradient of the sum and difference of two functions-
If f and g are two scalar point functions, then
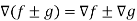
Proof:
L.H.S 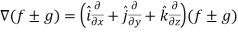
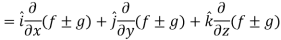
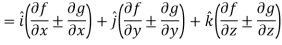
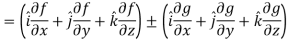
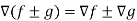
Hence proved
Property-4: Gradient of the product of two functions
If f and g are two scalar point functions, then
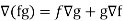
Proof:
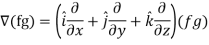
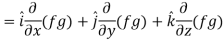
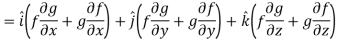
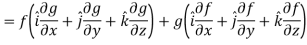
So that-
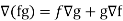
Hence proved.
Property-5: Gradient of the quotient of two functions-
If f and g are two scalar point functions, then-
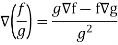
Proof:
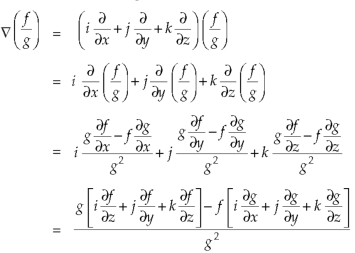
So that-
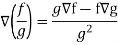
Example-1: If 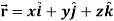 , then show that
, then show that
1. 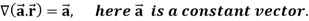
2. 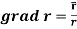
Sol.
Suppose 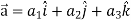 and
and 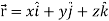
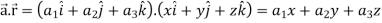
Now taking L.H.S,
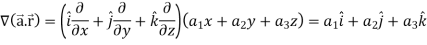
Which is 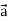
Hence proved.
2. 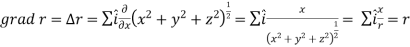
So that
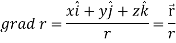
Example: If 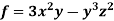 then find grad f at the point (1,-2,-1).
then find grad f at the point (1,-2,-1).
Sol.
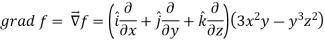

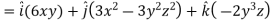
Now grad f at (1 , -2, -1) will be-
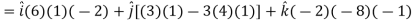
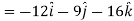
Example: If 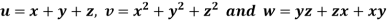 then prove that grad u , grad v and grad w are coplanar.
then prove that grad u , grad v and grad w are coplanar.
Sol.
Here- 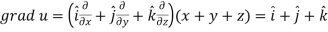
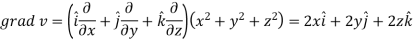
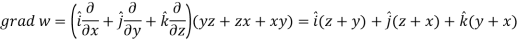
Now-
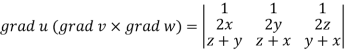
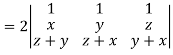
Apply 
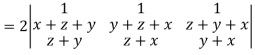
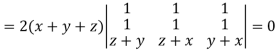
Which becomes zero.
So that we can say that grad u, grad v and grad w are coplanar vectors.
Divergence (Definition)-
Suppose 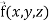 is a given continuous differentiable vector function then the divergence of this function can be defined as-
is a given continuous differentiable vector function then the divergence of this function can be defined as-
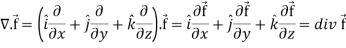
Curl (Definition)-
Curl of a vector function can be defined as-
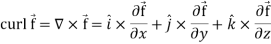
Note- Irrotational vector-
If 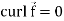 then the vector is said to be irrotational.
then the vector is said to be irrotational.
Vector identities:
Identity-1: grad uv = u grad v + v grad u
Proof:
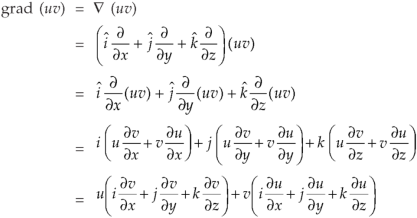
So that
Grad(uv) = u grad v + v grad u
Identity-2: 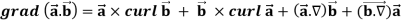
Proof:
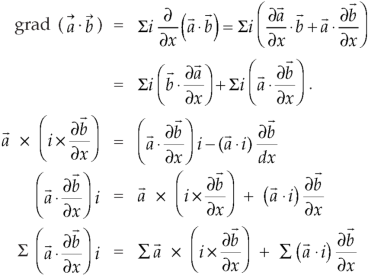
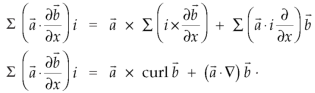
Interchanging  , we get-
, we get-
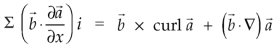
We get by using above equations-
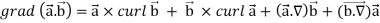
Identity-3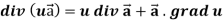
Proof: 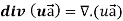
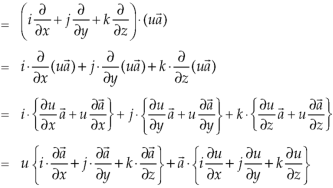
So that-
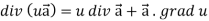
Identity-4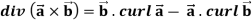
Proof:
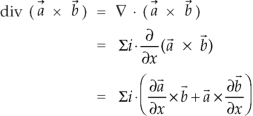
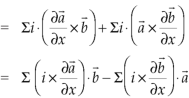
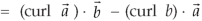
So that,
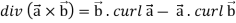
Identity-5 curl (u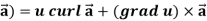
Proof:
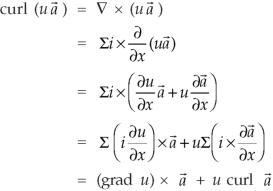
So that
Curl (u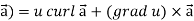
Identity-6: 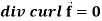
Proof:
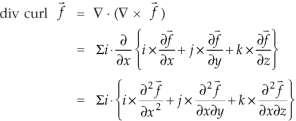
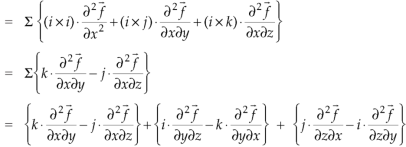
So that-
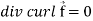
Identity-7: 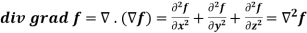
Proof:
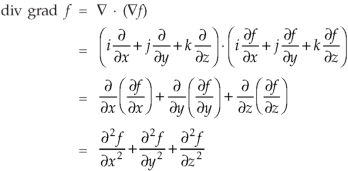
So that-
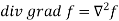
Example-1: Show that-
1. 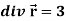
2.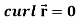
Sol. We know that-
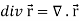
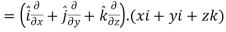
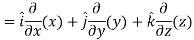
2. We know that-
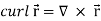
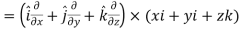
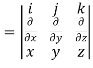
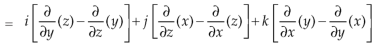
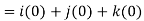 = 0
= 0
Example-2: If 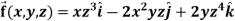 then find the divergence and curl of
then find the divergence and curl of 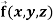 .
.
Sol. we know that-
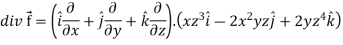
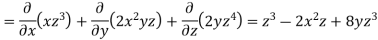
Now-
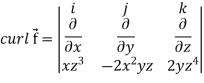
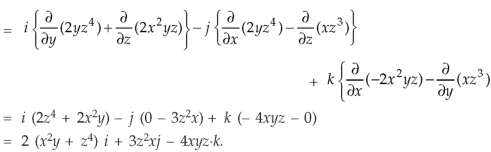
Example-3: Prove that 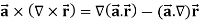
Note- here 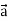 is a constant vector and
is a constant vector and 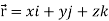
Sol. Here 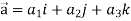 and
and 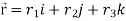
So that
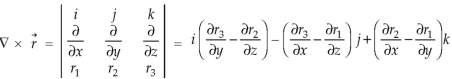
Now-
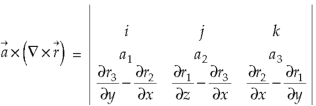
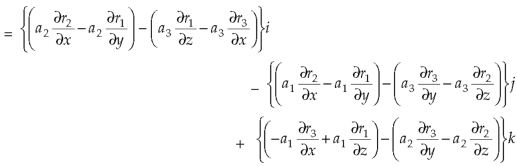
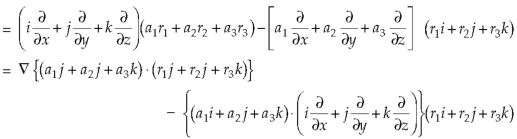
So that-
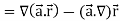
Key takeaways-
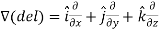
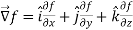
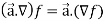
- Gradient of a constant (
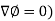
If f and g are two scalar point functions, then
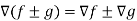
5. If f and g are two scalar point functions, then
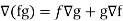
6. If f and g are two scalar point functions, then-
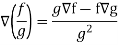
7. 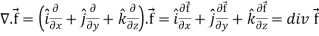
8. 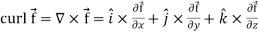
9. If  then the vector is said to be irrotational.
then the vector is said to be irrotational.
10. grad uv = u grad v + v grad u
11. 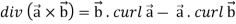
12. curl (u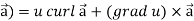
Let ϕ be a scalar point function and let ϕ(P) and ϕ(Q) be the values of ϕ at two neighbouring points P and Q in the field. Then,
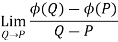
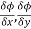 ,
,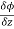 are the directional derivative of ϕ in the direction of the coordinate axes at P.
are the directional derivative of ϕ in the direction of the coordinate axes at P.
The directional derivative of ϕ in the direction l, m, n= l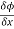 + m
+ m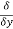 +
+ 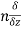
The directional derivative of ϕ in the direction of 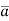 =
= 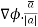
Example: Find the directional derivative of 1/r in the direction 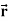 where
where 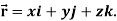
Sol. Here 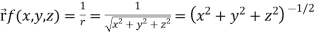
Now,
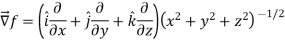
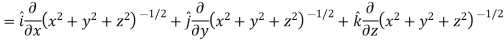
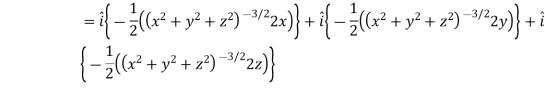
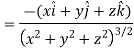
And 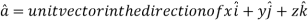
We know that-

So that-
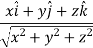
Now,
Directional derivative-
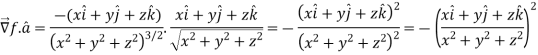
Example: Find the directional derivative of
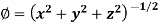
At the points (3, 1, 2) in the direction of the vector 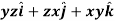 .
.
Sol. Here it is given that-
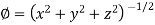
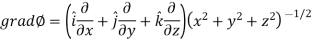
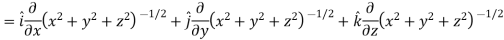
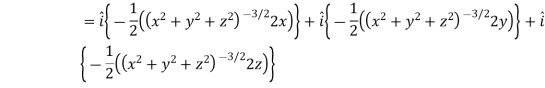
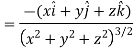
Now at the point (3, 1, 2)-
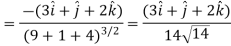
Let 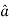 be the unit vector in the given direction, then
be the unit vector in the given direction, then
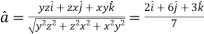 at (3, 1, 2)
at (3, 1, 2)
Now,
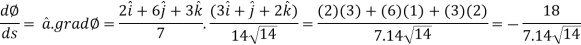
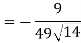
Example: Find the directional derivatives of 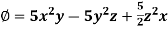 at the point P(1, 1, 1) in the direction of the line
at the point P(1, 1, 1) in the direction of the line 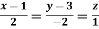
Sol. Here
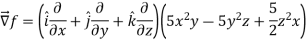
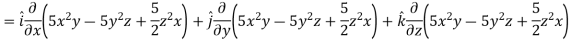
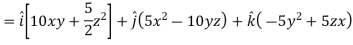
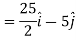
Direction ratio of the line 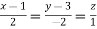 are 2, -2, 1
are 2, -2, 1
Now directions cosines of the line are-
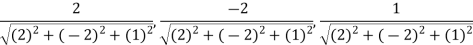
Which are 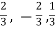
Directional derivative in the direction of the line-
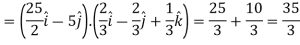
Key takeaways-
- The directional derivative of ϕ in the direction l, m, n= l
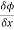 + m
+ m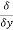 +
+ 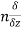
- The directional derivative of ϕ in the direction of
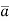 =
= 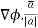
Solenoidal field-
A solenoidal field F is characterised by the following conditions-
1. 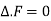
2. Flux 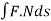 along every closed surface is zero.
along every closed surface is zero.
3. 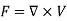
Note- In an solenoidal field for which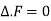 , the vector F can always be expressed as the curl of a vector function V.
, the vector F can always be expressed as the curl of a vector function V.
So that-
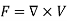
Irrotational field-
An irrotatonal field F is characterised by the following conditions-
1. 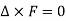
2. Circulation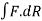 along every closed surface is zero.
along every closed surface is zero.
3. 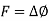
Note- In an irrotational field for which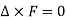 , the vector F can always be expressed as the gradient of a scalar function
, the vector F can always be expressed as the gradient of a scalar function 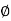 provided the domain is simply connected.
provided the domain is simply connected.
So that-
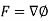
Here the scalar function is called the potential.
Example-1: Prove that the vector field 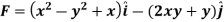 is irrotational and find its scalar potential.
is irrotational and find its scalar potential.
Sol. As we know that if 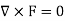 then field is irrotational.
then field is irrotational.
So that-
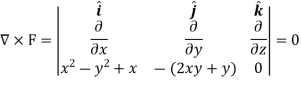
So that the field is irrotational and the vector F can be expressed as the gradient of a scalar potential,
That means-
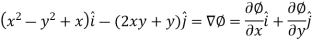
Now-
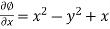 ………………… (1)
………………… (1)
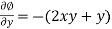 ……………………. (2)
……………………. (2)
Integrating (1) with respect to x, keep ‘y’ as constant-
We get-
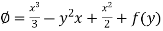 …………….. (3)
…………….. (3)
Integrating (1) with respect to y, keep ‘x’ as constant-
We get-
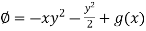 …………….. (4)
…………….. (4)
Equating (3) and (4)-
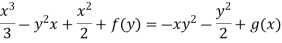
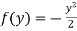 and
and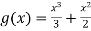
So that-
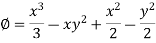
Example-2: Prove that the vector field 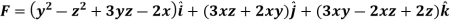 is solenoidal and irrotational.
is solenoidal and irrotational.
Sol. We know that if 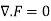 then the vector field will be solenoidal.
then the vector field will be solenoidal.
So that-
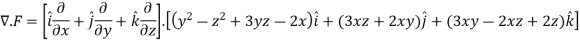
= 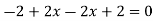
So that the vector field is solenoidal.
Now for irrotational field we need prove- 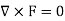
So that-
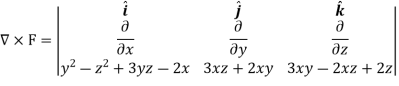
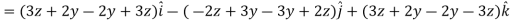
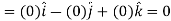
Thus, the vector field F is irrotational.
Example-3: Show that the vector field 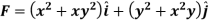 is irrotational and find the scalar potential function.
is irrotational and find the scalar potential function.
Sol. Now for irrotational field we need prove- 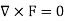
So that-
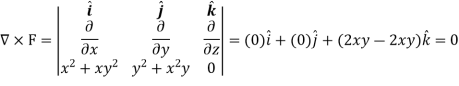
So that the vector field is irrotational.
Now in order to find the scalar potential function-
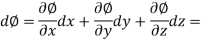
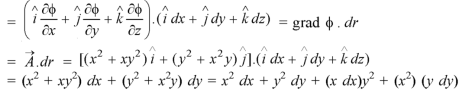
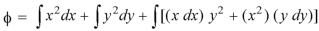
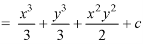
Key takeaways-
- In an solenoidal field for which
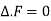 , the vector F can always be expressed as the curl of a vector function V.
, the vector F can always be expressed as the curl of a vector function V.
So that-
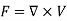
2. An irrotatonal field F is characterised by the following conditions-
1. 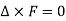
2. Circulation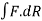 along every closed surface is zero.
along every closed surface is zero.
3. 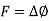
3. In an irrotational field for which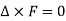 , the vector F can always be expressed as the gradient of a scalar function
, the vector F can always be expressed as the gradient of a scalar function 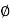 provided the domain is simply connected.
provided the domain is simply connected.
So that-
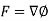
Here the scalar function is called the potential.
References
1. Erwin Kreyszig, Advanced Engineering Mathematics, 9thEdition, John Wiley & Sons, 2006.
2. N.P. Bali and Manish Goyal, A textbook of Engineering Mathematics, Laxmi Publications.
3. Higher engineering mathematic, Dr. B.S. Grewal, Khanna publishers
4. HK dass, engineering mathematics.