Unit-3
Analysis of Pin-Jointed Plane Frames
3.1.1 Pin-jointed statically determinate plane trusses-perfect frames, assumptions
Trusses are simply defined as triangulation of members to make the stabilized structure. Triangulation is the stable configuration mathematically. Generally, a truss has the members called as top chord, bottom chord, vertical chord and diagonal chord. The main functions of the trusses are:
- Carrying the loads from the over structures
- Providing adequate lateral stability to the entire structure
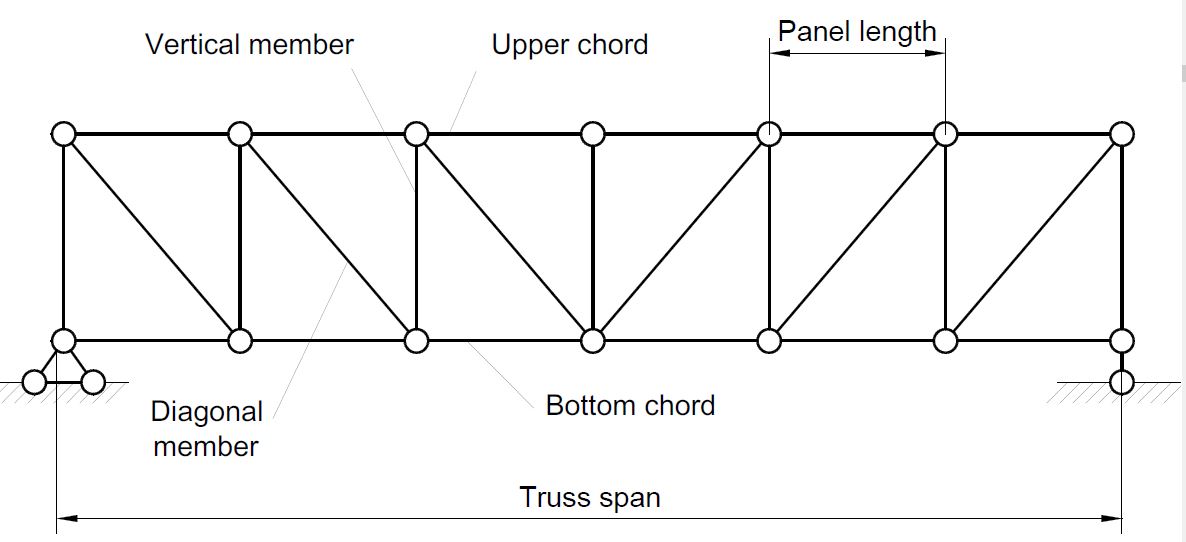
Fig 1
There are some basic assumptions in the designing process. It should be clarified that the construction of the trusses should conform with the design assumptions to avoid the unwanted failures due to the dispersion of the forces and loads.
Following are the assumptions in truss design.
- Truss members will carry only the axial forces
- The nodes i.e. the connections of the members are designed as pinned joints so that moments won’t be transferred to the members of the truss
- All the external loads and the reactions are act only on the nodes
- Generally, the truss should be in a plane.
- Typically the members of the trusses are made as I sections, angles, T sections, Tube sections, Square sections and channel sections. I sections are more preferable as an optimized section in terms of the structural forces.
TYPES OF TRUSSES
- Simple truss – indicates a single triangular truss. These trusses are most often used as the roof trusses.
- Planar truss – as the name implies it is a two dimensional truss. If all the members and the nodes are in a planar surface, then this truss is a planar truss.
- Space frame truss – Contrast to planar truss, the members and the nodes are located in the three dimensional space. Electrical and telecom towers are the one of the simplest example that we are seeing in the day to day life.
Simple Truss: It is possible to create a simple truss by joining three bars together to form a triangle. We can increase the size of the truss by adding two more members with an additional joint. By repeating this process, we can develop simple trusses with different shapes as shown below. The triangular building block assures internal stability of the truss structure as it is increased in size.
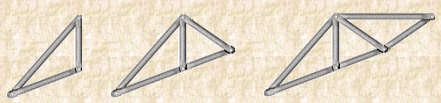
Fig 2
Although it is possible to have non-triangular cells in a simple truss, internal stability will not be guaranteed in that case.
Compound Truss: A compound truss is made up of simple trusses joined together to form a larger truss. The figure below shows a compound truss consisting of two simple trusses joined by a common joint and a bar. It is also possible to have multiple simple trusses joined together to create a larger compound truss. The connection of simple trusses then becomes a design issue determined based on the size of the resulting compound truss. Compound trusses are commonly used to support loads over long spans as in bridges.
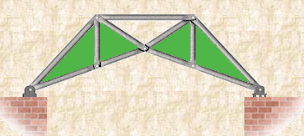
Fig 3
Complex Truss: A complex truss uses a general layout of members different from that used in simple and compound trusses. It often incorporates overlapping members.
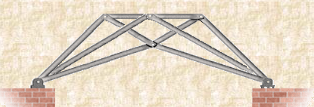
Fig 4
Key points
1) Simple truss – indicates a single triangular truss. These trusses are most often used as the roof trusses.
2) Planar truss – as the name implies it is a two dimensional truss. If all the members and the nodes are in a planar surface, then this truss is a planar truss
3.1.2 Determination of nature and magnitude of a force in a member
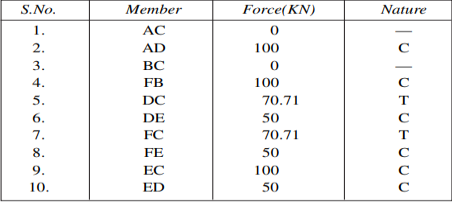
We can easily understand by assuming the magnitude and nature of forces in the various members of the truss shown in figure.
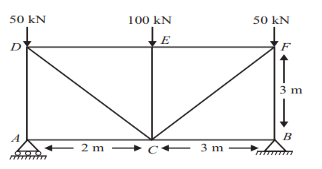
Fig 5
For Equilibrium
∑H = 0;
RBH = 0
∑V = 0;
RAV + RBV = 200
∑MB = 0;
RAV X 6 – 50 X 6 – 100 X 3 = 0
RAV = 100 KN And RBV = 100KN
Consider joint A;
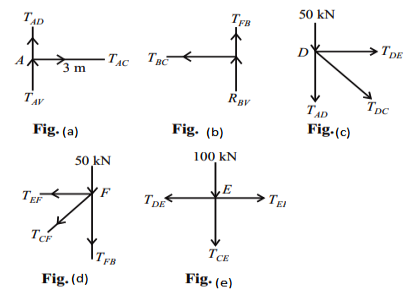
Fig (6)
∑H = 0;
TAC = 0
∑V = 0;
RAV + TAD = 0
TAD = – 100 KN(C)
Consider joint B;
As shown in fig(b)
∑H = 0;
TBC = 0
∑V = 0;
RBV + TFB = 0
TFB = – 100 KN
Consider joint D;
As shown in fig(c) ∑V = 0;
– TAD – TDC sin 45 – 50 = 0
TDC = 70.71KN (T)
∑H = 0;
TDE + TDC cos 45 = 0
TDE = – 50KN (C) Consider joint F;
As shown in fig (d)
∑V = 0;
– TFB – TFC sin 45 – 50= 0
TFC = 70.71KN (T)
∑H = 0;
– TFE – TFC cos 45 = 0
TFE = – 50KN (C)
Consider joint E; as shown in fig(e)
∑V = 0;
– TEC – 100 = 0
TEC = – 100KN (C)
∑H = 0;
– TED + TEF = 0
TED = – 50KN (C)
3.1.3 Simple trusses zero force members.
If a joint has only two non-collinear members and there is no external load or support reaction at that joint, then those two members are zeroforce members. In this example members DE, DC, AF, and AB are zero force members. Zero-force members can be removed (as shown in the figure) when analyzing the truss.
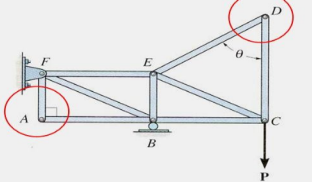
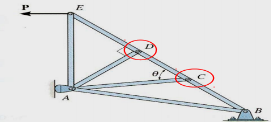
Fig 7
If three members form a truss joint for which two of the members are collinear and there is no external load or reaction at that joint, then the third non-collinear member is a zero force member, e.g., DA
Again, this can easily be proven. One can also remove the zero-force member, as shown, on the left, for analyzing the truss further. Please note that zero-force members are used to increase stability and rigidity of the truss, and to provide support for various different loading conditions
Zero force members in a truss are members which do not have any force in them (obviously...). There are two rules that may be used to find zero-force members in a truss. These are described below and illustrated in Figure 3.3.
Case 1
At a TWO member joint: If those members are NOT parallel AND there are no other external loads (or reactions) at the joint THEN both of those members are zero force members.
Case 2
In a THREE member joint: If TWO of those members ARE parallel AND there are no other external loads (or reactions) at the joint THEN the member that is not parallel is a zero force member.
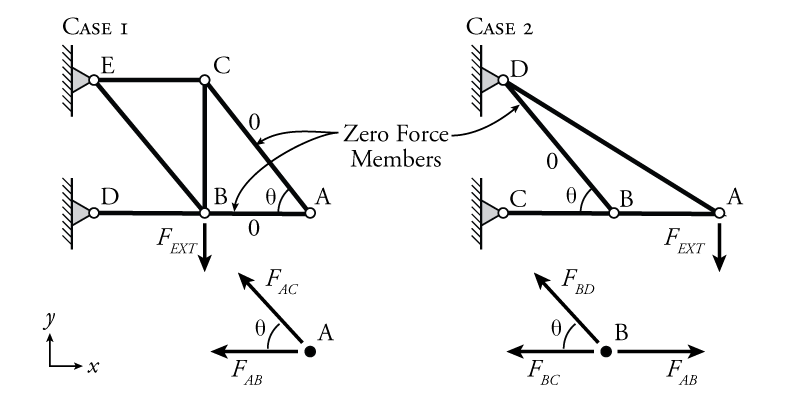
Figure 8: Examples of Zero Force Members
Two examples, one for each case, are shown in Figure 13. By applying equilibrium to the appropriate joints, we can see why the members shown do not have any force.
For the case 1 example, members AB and AC are zero force members. This may be shown to be the case by solving the equilibrium equations (1)(1) at joint A.
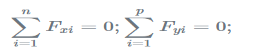
For vertical equilibrium (yy-direction), the vertical component of FAC is the only vertical force:
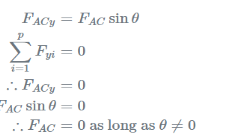
Therefore, FAC is a zero-force member. If we now apply horizontal equilibrium (xx-direction), we have two horizontal forces, FABFAB and the horizontal component of FAC:
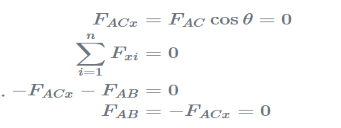
Therefore, FAB must also be a zero force member. In this example FACx and FAB are both negative because the arrows both point to the left. This analysis works for any two loads at joint which are not parallel where there is no external load on the joint.
For case 2 in Figure 3.3, member BD is a zero force member. This may be shown to be the case by solving the equilibrium equations (1)(1) at joint B. For vertical equilibrium, the vertical component of FBDFBD is the only vertical force:
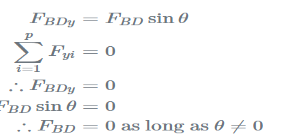
Therefore FBD is a zero-force member. This analysis was simplified because the members BC and AB were parallel to the xx-axis; however, the orientation of the xx-axis is arbitrary, an analysis will show that member BD is a zero force member as long as two of the members are parallel at the joint, even if they are not parallel to the xx- or yy-axis (try it out!).Finding these zero force members up front can save analysis time and effort.
Method of joint: This method involves isolating each joint of the truss and considering the equilibrium of the joint when determining the member axial force. Two equations used in determining the member axial forces are ∑ Fx = 0 and ∑ Fy = 0. Joints are isolated consecutively for analysis based on the principle that the number of the unknown member axial forces should never be more than two in the joint under consideration in a plane trust.
Analysis of Trusses by Method of Joint
This method is based on the principle that if a structural system constitutes a body in equilibrium, then any joint in that system is also in equilibrium and, thus, can be isolated from the entire system and analyzed using the conditions of equilibrium. The method of joint involves successively isolating each joint in a truss system and determining the axial forces in the members meeting at the joint by applying the equations of equilibrium. The detailed procedure for analysis by this method is stated below.
Procedure for Analysis
•Verify the stability and determinacy of the structure. If the truss is stable and determinate, then proceed to the next step.
•Determine the support reactions in the truss.
•Identify the zero-force members in the system. This will immeasurably reduce the computational efforts involved in the analysis.
•Select a joint to analyse. At no instance should there be more than two unknown member forces in the analysed joint.
•Draw the isolated free-body diagram of the selected joint, and indicate the axial forces in all members meeting at the joint as tensile (i.e. as pulling away from the joint). If this initial assumption is wrong, the determined member axial force will be negative in the analysis, meaning that the member is in compression and not in tension.
•Apply the two equations Σ Fx = 0 and Σ Fy = 0 to determine the member axial forces.
•Continue the analysis by proceeding to the next joint with two or fewer unknown member forces.

Fig 9
Method of section: This method entails passing an imaginary section through the truss to divide it into two sections. The member forces are determined by considering the equilibrium of the part of the truss on either side of the section. This method is advantageous when the axial forces in specific members are required in a truss with several members.
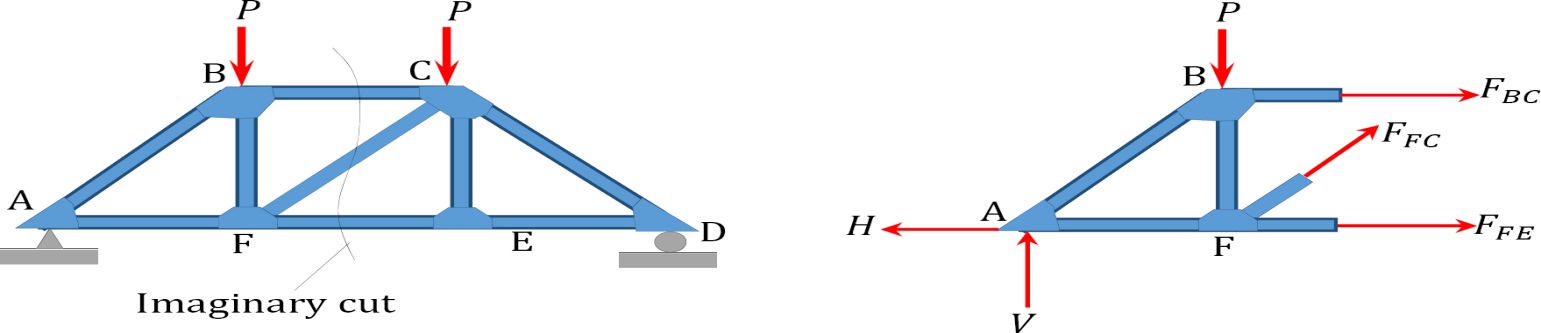
Fig 10
Analysis of Trusses by Method of Section
Sometimes, determining the axial force in specific members of a truss system by the method of joint can be very involving and cumbersome, especially when the system consists of several members. In such instances, using the method of section can be timesaving and, thus, preferable. This method involves passing an imaginary section through the truss so that it divides the system into two parts and cuts through members whose axial forces are desired. Member axial forces are then determined using the conditions of equilibrium. The detailed procedure for analysis by this method is presented below.
Procedure for Analysis of Trusses by Method of Section
•Check the stability and determinacy of the structure. If the truss is stable and determinate, then proceed to the next step.
•Determine the support reactions in the truss.
•Make an imaginary cut through the structure so that it includes the members whose axial forces are desired. The imaginary cut divides the truss into two parts.
•Apply forces to each part of the truss to keep it in equilibrium.
•Select either part of the truss for the determination of member forces.
•Apply the conditions of equilibrium to determine the member axial forces.
Reference
1. Engineering Mechanics by S. P. Timoshenko and D. H. Young, McGraw- Hill publication
2. Engineering Mechanics by F L Singer, Harper and Rowe publication
3. Engineering Mechanics by A. P. Boresi and R. J. Schmidt, Brooks/Cole Publication