Unit-8
Mechanical Vibrations
Vibration terminology consists of 12 terms which are:
- Periodic Motion
- Time Period
- Cycle
- Frequency
- Amplitude
- Natural Frequency
- The fundamental mode of vibration
- Degree of freedom
- Simple harmonic motion
- Damping
- Resonance
- Mechanical System
1. Periodic Motion:
The motion which repeats itself after an equal interval of times is called Periodic motion.
2. Time Period:
This is defined as time to complete one cycle is called a Time period and it is normally expressed in seconds (s).
3. Cycle:
It is motion completed during one time period
4. Frequency:
This is defined as the number of cycles describes in one second.
This SI unit is Hertz
5. Amplitude:
The maximum displacement of the vibrating body from its equilibrium position
6. Natural frequency:
When no external force acts on the system after giving it’s an initial displacement, the body vibrates. The vibration is called as free vibration and the frequency is called Natural frequency. This is expressed in rad/sec or Hertz.
7. The fundamental mode of vibration:
The fundamental mode of vibration is the model having the lowest natural frequency.
8. Degree of Freedom:
The minimum number of independent coordinates requires specifying the motion of a system at any instant is known as the degree of freedom.
9. Simple Harmonic Motion:
The motion of the body to and fro about a fixed point is called simple harmonic motion
10. Damping:
It is resistance to the motion of a vibrating body. The vibration associated with the resistance is known as Damped Vibration.
11. Resonance:
When the frequency of external excitation is equal to the natural frequency of the vibrating body, the amplitude of vibration becomes excessively large. This concept is called resonance.
12. Mechanical System:
The system consists of Mass, stiffness, and damping are known as a mechanical system.
Free vibrations are oscillations where the total energy stays the same over time. This means that the amplitude of the vibration stays the same. This is a theoretical idea because in real systems the energy is dissipated to the surroundings over time and the amplitude decays away to zero, this dissipation of energy is called damping.
The free oscillation possesses constant amplitude and period without any external force to set the oscillation. Ideally, free oscillation does not undergo damping. But in all-natural systems damping is observed unless and until any constant external force is supplied to overcome damping. In such a system, the amplitude, frequency and energy all remain constant.
Free vibration

Light damping

Heavy damping

Critical damping

Over damped
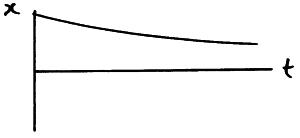
Fig 1
Forced vibrations occur when the object is forced to vibrate at a particular frequency by a periodic input of force.
Objects which are free to vibrate will have one or more natural frequency, at which they vibrate,
If an object is being forced to vibrate at its natural frequency, resonance will occur and you will observe large amplitude vibrations. The resonant frequency is fo. When a body oscillates by being influenced by an external periodic force, it is called forced oscillation. Here, the amplitude of oscillation, experiences damping but remains constant due to the external energy supplied to the system.
For example, when you push someone on a swing, you have to keep periodically pushing them so that the swing doesn’t reduce.
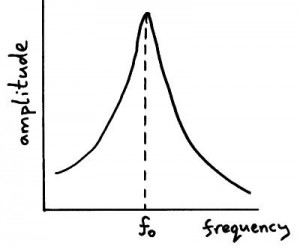
Fig 2-Effect of damping on resonance graph
The amplitude of the resonance peak decreases and the peak occurs at a lower frequency.
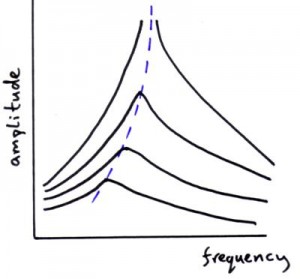
Fig 3
Resonance and its effects
Resonance – Resonance is a special case of forced vibrations. When the frequency of an externally applied periodic force on a body is equal to its natural frequency, the body starts vibrating with increased amplitude. This phenomenon is called resonance and the vibrations of large amplitude are called resonant vibrations.
Resonance is a condition that can occur in mechanical structures and can be described as sensitivity to a certain vibration frequency. Resonance occurs when a natural frequency is at or close to a forcing frequency, such as rotor speed. For machinery such as pumps, turbines and electric motors resonance can amplify the small vibratory forces from machine operation, and severe vibration levels can result. Such problems often develop after a speed change has been implemented, as with retrofitting a machine with an adjustable-speed drive (ASD) or operating a 50-hertz motor on 60 hertz of power.
The solution to these problems frequently depends on distinguishing between structural resonance and a rotor critical speed. Structural resonance refers to excessive vibrations of non-rotating components, usually machine components or supporting structures. Rotor critical speed refers to a condition in which the speed of the rotating element of the machine matches the rotor’s natural frequency.
Condition for resonance – Resonance occurs when the frequency of the applied force is exactly equal to the natural frequency of the vibrating body.
The Characteristics of Resonance
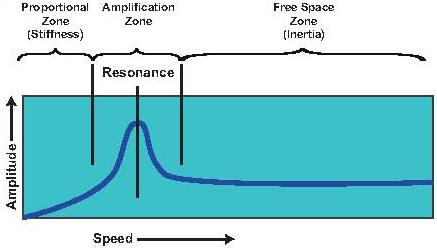
Fig 4
The most notable characteristic of resonance is increased vibration when a certain operating speed is reached. Also, as the operating speed is increased beyond the resonant frequency, the vibration amplitude will decrease somewhat. The Bode plot in Figure 1 shows the operating speed versus the amplitude. For the sake of illustration, assume that the exciting force is residual unbalance of the rotor at the rotating speed.
The formula for calculating the natural frequency is:
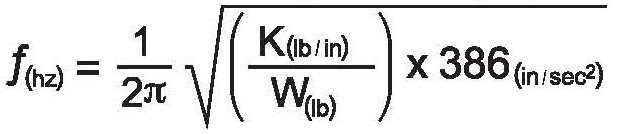
Where “K” is the stiffness of the resonant structure or component, and “W” is the weight (mass). Note that at the core of this formula is:
K/W = stiffness/mass
Increased stiffness will, therefore, raise the natural frequency, and increased mass will lower it. That is logical since stiffness creates a force that is always directed against motion, while mass has inertia, which is a force always directed with motion. Resonance is what happens when these two opposing forces are equal. They cancel each other out, allowing vibration to increase.
Examples of resonance
- Sympathetic vibrations of pendulums
- Resonance in machine parts
- Resonance in a stretched string and sound box of musical instruments and sonometer
- Resonance in air column and tuning fork
- Resonance in a bridge
- Resonance in radio and TV receivers
Degree of freedom
Degree of freedom is defined as the minimum number of independent variables required to define the position or motion of a system is known as degree of freedom. Degree of freedom is the property of kinematic chain which shows that in how many directions the connected links of the kinematic can move freely. It is also known by mobility.

Fig 5
In 3-D space system an unconstrained rigid body possesses six degree of freedom. Total number of motions in space is six as 3 are rotary and 3 are translator along x, y and z axis respectively. Here DOF can also be defined as the subtraction of total number of motions and the number of motions restraints or arrested (those motions which are not possible).
DOF = 6 – Restraints
In 2-D space system maximum 3 motions can be predicted as 2 translatory motion along x and y axis respectively and 1 rotary in perpendicular to x-axis i.e. z-axis.
DOF = 3 – Restraint
To determine DOF of 2-D planar mechanism, Kutzback was a scientist who gave the relation
DOF = 3(L-1) – 2j – h
Where
L = number of links
j = number of joints
h = number of higher pairs
Sometimes a system may have one or more links of a mechanism which do not introduce any extra constraint, such links are known as redundant links and should not be counted to find the DOF and also corresponding joint will not be counted.
Sometimes one or more links of a mechanism can be moved without causing any motion to the rest of the links of the mechanism, such a link is said to have redundant DOF. Due to this DOF formula for planar mechanism is modified.
DOF = 3(L-1) – 2j – h – Fr
Where,
Fr = redundant motion
Now Grubler was another scientist, he utilized the Kutzback equation and gave his formulation i.e. he used the equation and put DOF equal to 1 and higher pair equal to zero for a kinematic chain. Grubler’s criterion was the extension of Kutzback equation and expressed as
DOF = 3(L-1) – 2j – h
1 = 3(L-1) – 2j – 0
3L – 2j – 4 = 0 (this is the derived equation of Grubler’s criterion.)
From Grubler’s criterion it is clear that to hold the equation number of links should be even i.e. minimum number of links required is 4.
Key points
1) The formula for calculating the natural frequency is:

2) DOF formula for planar mechanism is modified.
DOF = 3(L-1) – 2j – h – Fr
3) K/W = stiffness/mass
Where “K” is the stiffness of the resonant structure or component, and “W” is the weight (mass).
Reference
1. Engineering Mechanics by S. P. Timoshenko and D. H. Young, McGraw- Hill publication
2. Engineering Mechanics by J. L. Meriam and Craige, John Willey