UNIT -2
CRYSTALLOGRAPHY
UNIT CELL
BASICS OF CRYSTAL STRUCTURE
Crystallography is the experimental science of determining the arrangement of atoms in the crystalline solids. The properties of some materials are directly related to their crystal structures. So first of we will see what crystal structure is. Crystal structure can be defined as
Crystal structure
A crystal is a solid in which the constituent atoms, molecules or ions are packed in a regularly ordered, repeating pattern extending in three dimensions.
Based on the atomic arrangement in a substance, solids can be broadly classified as either crystalline solids or amorphous solids.
Crystalline Solids
In a crystalline solid, all the atoms are arranged in a periodic manner in all three dimensions. Crystalline solids need extreme temperatures to break the intermolecular forces. They have a definite heat of fusion and melting points because of the uniform arrangement of their components. The local environment is also uniform. However, when cut in any direction, the physical properties are different thus known as anisotropic. When rotated around the axis, the structure of crystals remains the same and that is termed as symmetrical arrangement of molecules, atoms or ions. The refractive index, mechanical strength, thermal conductivity and electrical conductivity of crystalline solids differ in different directions.
Amorphous solids
In a non-crystalline or amorphous solid the atomic arrangement is random or non-periodic in nature. The word amorphous is derived from the Greek word amorphous which means “shapeless”. This is the shapeless, disordered, and irregular arrangement of the constituent particles of a solid. Their inter-molecular forces are not the same nor are the distances between the particles. When cleaved, amorphous solids results in curved surfaces because of their irregular geometric shapes. Thermal conductivity, mechanical strength, electrical conductivity and refractive index are the same in all directions of amorphous solids. This explains where the name isotropic comes from. The solids do not have a sharp melting points or a definite heat of fusion. A wide range of temperature needs to be applied before they can melt because of the absence of an ordered array of components. Examples of amorphous solids include polymers, rubbers, plastics and glass.
Difference between Crystalline solids and amorphous solids
Crystalline solids | Amorphous solids |
|
|
2. They have long range order of regular pattern of arrangement of constituent particles. | 2. They have short range order of regular pattern of arrangement of constituent particles. |
3. They are true solids. | 3. They are pseudo solids or super cooled |
4. They have sharp melting points. | 4. They do not have sharp melting points. |
5. They are anisotropic in nature. | 5. They are isotropic in nature. |
6. They have definite heat of fusion. | 6. They do not have definite heat of fusion. |
Space Lattice or Crystal Lattice
In a solid crystalline material, the atoms or molecules are arranged regularly and periodically in all three dimensions. The atomic arrangement in a crystal is called crystal structure.
To explain crystal symmetries easily, it is convenient to represent an atom or a group of atoms that repeats in three dimensions in the crystal as a unit. If each such atom or unit of atoms in a crystal is replaced by a point in space, then the resultant points in space are called space lattice.
Each point in a space lattice is called a lattice point. Each atom or unit of atoms is called basis or pattern.
A space lattice or crystal lattice is defined as three dimensional infinite arrays of points in space in which every point has surroundings identical to that of every other point in the array.
Basis and Crystal Structure
The atomic arrangement in a crystal is called crystal structure. The crystal structure is formed by associating every lattice point with an atom or an assembly of atoms or molecules or ions, which are identical in composition, arrangement and orientation, called the basis. i.e. an atom, or a group of atoms or molecules identical in composition is called the basis or the pattern.
The basis provides the number of atoms per lattice point, their types, mutual orientations and distances of separation between the atoms.
If the basis is substituted for the lattice points, then the resulting structure is called crystal structure as shown in Figure.
Lattice + basis = crystal structure.
The basis shown in Figure contains two different atoms. In copper and sodium crystals the basis is single atoms; In NaCl, the basis is diatomic and in CaF2 the basis is triatomic. A lattice is an imaginary assumption while the crystal structure is a real concept.

Figure 1: Lattice sites, Basis and crystal structure
Unit Cell and Lattice Parameters
Unit cell is small repeating entity of the atomic structure. It is the basic building block of the crystal structure. It defines the entire crystal structure with the atom positions within.
Unit cells for most of the crystals are parallelepipeds or cubes having three sets of parallel faces. A unit cell is the basic structural unit or building block of the crystal.
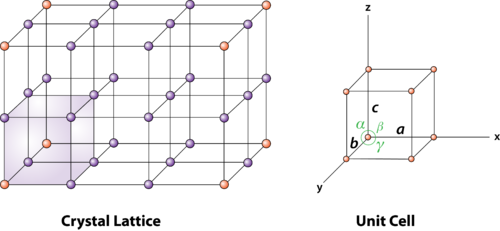
Figure 2: unit cell and unit cell parameter
A unit cell is defined as the smallest parallelepiped volume in the crystal, which on repetition along the crystallographic axes gives the actual crystal structure or the smallest geometric figure, which on repetition in three-dimensional space, gives the actual crystal structure is called a unit cell.
Choice of a unit cell is not unique but it can be constructed in a number of ways as shown in figure. Following figure shows different ways of representing unit cells in a two-dimensional lattice. A unit cell can be represented as ABCD or A′B′C′D′ or A′′B′′C′′D′′, etc.
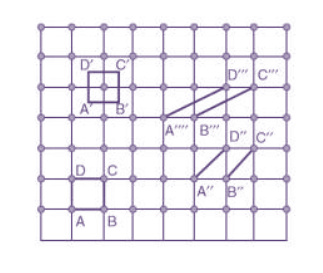
Figure 3: Construction of unit cell in different way
Unit cell parameters or lattice parameters
First, we define crystallographic axes. These axes are obtained by the intersection of the three non-coplanar faces of the unit cell. The angles between these faces or crystallographic axes are known as interfacial or interaxial angles. The angles between the axes Y and Z are α, between Z and X is β and between X and Y is γ. The translational vectors or primitives a, b, c of a unit cell along X, Y, Z axes and interaxial angles α, β, γ are called Cell parameters. These cell parameters are shown in (Figure 2). The cell parameters determine the actual size and shape of the unit cell.
Primitive and non-primitive unit cells
The unit cell formed by primitives is called a simple or a primitive unit cell. A primitive unit cell contains only one lattice point. If a unit cell contains more than one lattice point, then it is called a non-primitive unit cell or a multiple unit cell. Most of the unit cells of various crystal lattices contain two or more lattice points and hence it is not necessary that unit cell should be a primitive unit cell.
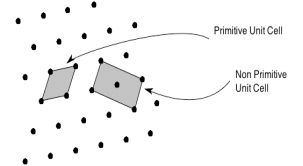
Figure 4: Primitive and non-primitive unit cells
BRAVAIS LATTICE
If the surroundings of each lattice point is same or if the atom or all the atoms at lattice points are identical, then such a lattice is called Bravais lattice.
A space lattice represents the geometrical pattern of crystal in which the surroundings of each lattice point is the same. If the surroundings of each lattice point is same or if the atom or all the atoms at lattice points are identical, then such a lattice is called Bravais lattice.
On the other hand, if the atom or the atoms at lattice points are not same, then it is said to be a non-Bravais lattice.
For representing the type of distribution of lattice points in space, seven different co-ordinate systems are required. These co-ordinate systems are called crystal systems.
The crystal systems are named on the basis of geometrical shape and symmetry. The seven crystal systems are:
(1) Cubic
(2) Tetragonal
(3) Orthorhombic
(4) Monoclinic
(5) Triclinic
(6) Trigonal (or Rhombohedral)
(7) Hexagonal.
In 1948, Bravais showed that 14 lattices are sufficient to describe all crystals. These 14 lattices are known as Bravais lattices and are classified into 7 crystal systems based on cell parameters or lattice points present per unit cell.
Bravais lattices are categorized as
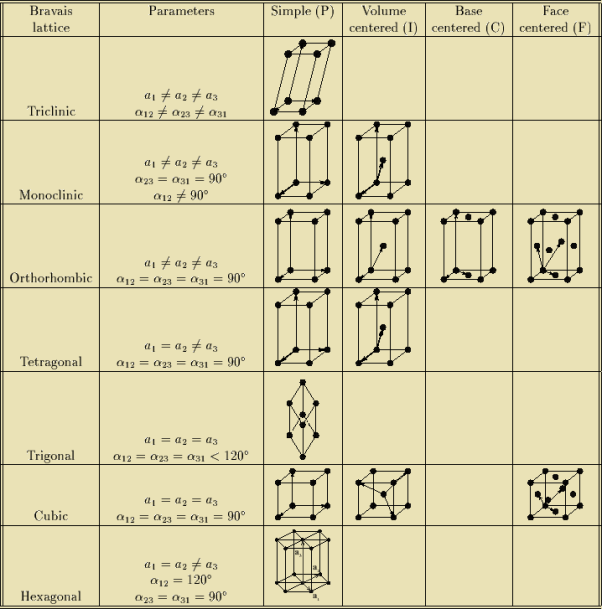
Figure 5: Bravais lattices
CUBIC SYSTEM
The cubic crystal system is one of the most common (and by far the simplest) class of crystals. As the name itself suggests, all crystal structures of this system have a cube-shaped unit cell with edge length given by the lattice parameter ‘a’.
The three main common representatives are:
- Simple or Primitive Cubic (SC) (also known as primitive cubic)
- Body-centered Cubic (BCC)
- Face-centered Cubic (FCC)
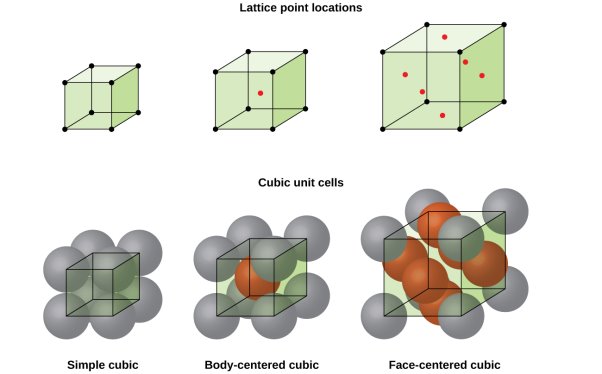
Figure 6: SC, BCC, FCC structure
NUMBER OF ATOMS PER UNIT CELL
Simple or Primitive lattice
In simple or primitive lattice, 8 lattice points or 8 atoms are present at the 8 corners of the unit cell, each contributing 1/8thto the unit cell and hence there will be 8 x 1/8 = 1 lattice point per unit cell.

Figure 7: simple or primitive lattice
Body-centered lattice
In body-centered lattice, in addition to the 8 atoms at 8 corners each contributing 1/8thto the unit cell, there will be one complete atom at the center of the unit cell. Therefore number of atoms or lattice points in a body centered unit cell becomes 8 x 1/8 + 1 x 1 = 2.

Figure 8: Body-centered lattice
Face-centered lattice (F)
In case of face-centered lattice, in addition to the 8 atoms at 8 corners each contributing 1/8thto the unit cell, six atoms will be present at the center of six faces of the cell each contributing 1/2nd to the unit cell. Therefore number of atoms or lattice points in a face centered unit cell becomes 8 x 1/8 + 6 x 1/2 = 4.
Figure 9: Face-centered lattice (F)
COORDINATION NUMBER
The number of nearest neighbour atoms or ions surrounding an atom or ion is known as coordination number.
It is measure of closeness of packing of atoms in any given structure. It equals the number of nearest neighbour that surrounds each atom.
Simple or Primitive Cubic Crystal
In simple cubic system 6 neighbours atoms at a distance of ‘a’ each from the selected atom as shown in figure. So the coordination number of SC is six.
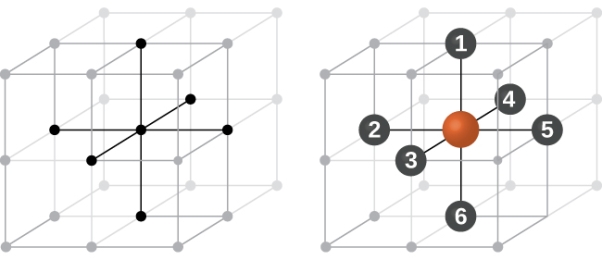
Figure 10: Simple Cubic Crystal
Body Centred Cubic Crystal
In Body Centred Cubic system 8 neighbour atoms are in touch with the selected atom as shown in figure. So the coordination number of BCC is eight.

Figure 11: Body Centred Cubic Crystal
Face Centred Cubic Crystal
In Face Centred Cubic system 12 neighbour atoms are in touch with the selected atom as shown in figure. So the coordination number of FCC is twelve.

Figure 12: Face Centred Cubic Crystal
ATOMIC RADIUS
Atoms are not hard spheres with distinct boundaries, so their sizes are not determined directly. However, the positions of the atoms in a solid can be determined by x-ray diffraction, and the sizes of the atoms are inferred from those distances.
In this method, the radius of an atom is determined from the unit cell edge length (a), which is determined from the location of the atoms, and the assumption that the atoms touch as shown in below.
Simple or Primitive Cubic Crystal

2r = a
Figure 13: Simple or Primitive Cubic Crystal
Body Centred Cubic Crystal
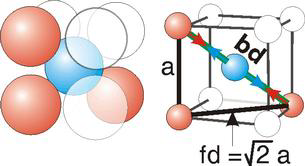
Figure 14: Body Centred Cubic Crystal
Bd | = | 4r |
|
|
|
|
|
|
Bd2 | = | Fd2 + a2 |
|
|
|
|
|
|
(4r)2 | = | 2a2 + a2 = 3a2 |
Face Centred Cubic Crystal
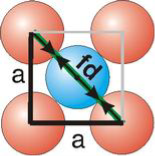
Figure 15: Face Centred Cubic Crystal
Fd | = | 4r |
|
|
|
|
|
|
Fd2 | = | a2 + a2 |
|
|
|
|
|
|
(4r)2 | = | 2a2 |
Relationship of Atomic Radii and Unit Cell Edge Lengths
Setting the edge length equal to 2r in the sc unit cell, and applying the Pythagorean theorem to the triangles shown in Figures we obtain the relationships between the atomic radius (r) of the atom and the edge length of the unit cell (a) given in Equation
For SC r = a/2
For BCC r = 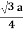
For FCC r = 
Key Takeaways
- A crystal is a solid in which the constituent atoms, molecules or ions are packed in a regularly ordered, repeating pattern extending in three dimensions.
- Based on the atomic arrangement in a substance, solids can be broadly classified as either crystalline solids or amorphous solids.
- Each point in a space lattice is called a lattice point. Each atom or unit of atoms is called basis or pattern.
- A space lattice or crystal lattice is defined as three dimensional infinite arrays of points in space in which every point has surroundings identical to that of every other point in the array.
- Unit cell is small repeating entity of the atomic structure. It is the basic building block of the crystal structure. It defines the entire crystal structure with the atom positions within.
- If the surroundings of each lattice point is same or if the atom or all the atoms at lattice points are identical, then such a lattice is called Bravais lattice.
- The number of nearest neighbour atoms or ions surrounding an atom or ion is known as coordination number.
- Relationship of Atomic Radii and Unit Cell Edge Lengths is given as
For SC r = a/2 , For BCC r = 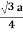 . For FCC r =
. For FCC r = 
2.2.1 ATOMIC PACKING FACTOR, VOID SPACE, DENSITY OF CRYSTAL
It is impossible to pack spheres without introducing some void space (space that is not occupied). How well the atoms pack a unit cell depends upon the unit cell type and is given by the packing efficiency of the unit cell. Solids with tightly packed unit cells are denser than those with low packing efficiencies. In this section, we examine the packing efficiencies of the cubic unit cells and show how to determine the density of a solid from its crystal structure.
Density
Density is the mass-to-volume ratio of a substance.
Density d = mass of substance / volume of substance
|
Packing Efficiency
Packing efficiency is the fraction of the unit cell that is occupied by particles. Spheres cannot be packed without creating some void space, but the amount of void space depends upon how well they are packed. Packing efficiency (PE) is that fraction of the unit cell volume that is actually occupied by particles, not void space. Thus, the packing efficiency of a unit cell is
Packing Fraction =  |
|
PE = 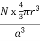 |
a = the length of a side of the unit cell, so a3 is the volume of the unit cell.
r = the radius of the atoms that occupy the unit cell, so (4/3)πr3 is the volume of a single atom in the unit cell.
N = the number of atoms in the unit cell, so N(4/3)πr3 is the volume occupied by all of the atoms in the unit cell.
The unit cell size (a) is directly proportional to the atom size (r), so one can be defined in terms of the other.
Consequently, the packing efficiency depends only upon the cell type, not its size. As shown in the next sections, the relationship between a and r depends only upon the unit cell type.
Packing in Simple Cubes
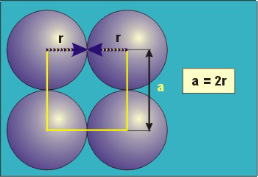
Figure 16: Simple or Primitive Cubic Crystal
In the simple cubic unit cell, the spheres touch along the cell edge. Consequently, the edge length is two atomic radii
(a = 2r).
The properties of the simple cubic unit cell:
r = 0.5a
N = 1 atom/unit cell
PE =  |
Packing efficiency = 52%
Coordination number = 6
Packing in Body-Centered Cubes
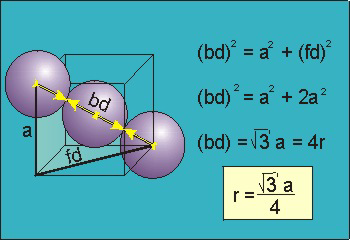
Figure 17: Body Centred Cubic Crystal
For the body-centered cubic unit cell, the spheres make contact along the body diagonal (bd), which is four atomic radii (each yellow arrow is one atomic radius), i.e., bd = 4r.
The body diagonal is related to the face diagonal (fd) and the cell edge (a) by the Pythagorean theorem. The relationship between the cell edge and the face diagonal was derived in the discussion of the fcc unit cell. The properties of the body-centered cubic unit cell:
For BCC r = 
r = 0.433 a
N = 2 atoms/unit cell
PE =  |
Packing efficiency = 68%
Coordination number = 8
Packing in Face-Centered Cubes
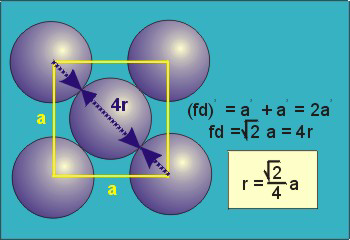
Figure 18: Face Centred Cubic Crystal
For FCC r = 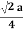
r= 0.354a
N = 4 atoms/unit cell
PE =  |
Packing efficiency = 74%
Coordination number = 12
As shown in the previous sections, the packing efficiency of a unit cell depends only on the cell type; it is independent of edge length and atomic radius because both cancel in the calculation. As might be expected, the packing efficiency increases as the number of atoms in the unit cell and the number of atoms that are packed around each atom (coordination number) increases.
Table: Packing Efficiencies and Coordination Numbers of Cubic Lattices
Lattice | Packing | Coordination |
Simple | 52% | 6 |
Body-centered | 68% | 8 |
Face-centered | 74% | 12 |
Table for Sc, Bcc, Fcc, Hcp Lattices
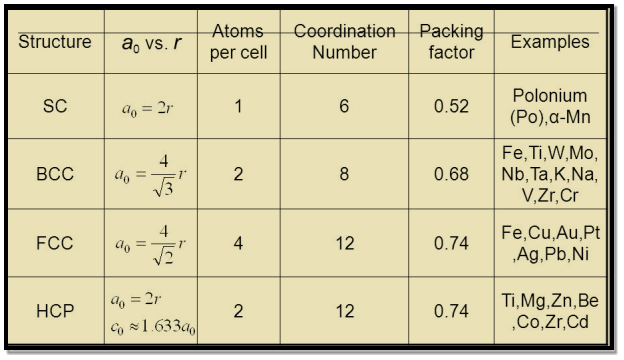
Figure 19: Table for Sc, Bcc, Fcc, Hcp Lattices
2.2.2 VOID SPACE
In the three-dimensional structure, both in CCP and HCP close packing in solids, about 26% of total space is vacant and is not covered by spheres. These empty spaces are known as the interstitial voids, interstices or holes. The above voids in solids depend on the number of spheres.
There are two types of interstitial voids in a 3D structure:
- Tetrahedral voids: In cubic close packed structure, spheres of the second layer lie above the triangular voids of the first layer. Each sphere touches the three spheres of the first layer. By joining the centre of these four spheres, it forms a tetrahedron and the empty space left over by joining the centre of these spheres forms a tetrahedral void.
In closed packed structure the number of tetrahedral voids is two times the number of spheres.
Let the number of spheres be n.
Then the number of tetrahedral voids will be 2n.
2. Octahedral voids: Adjacent to tetrahedral voids you can find octahedral voids. So now, what are Octahedral Voids? When the triangular voids of the first layer coincides with the triangular voids of the layer above or below it, we get a void that is formed by enclosing six spheres. This vacant space formed by combining the triangular voids of the first layer and that of the second layer are called Octahedral Voids.
If the number of spheres in a close-packed structure is n, then the number of octahedral voids will be n.

Figure 20: Tetrahedral and octahedral void
2.2.3 DENSITY OF CRYSTAL
The first important thing to understand is that a cubic crystal is made up a crystal lattice or a space lattice structure. And as we have studied before, a space lattice is made up of a repeating arrangement of unit cells. A unit cell is the most basic structure of a crystalline solid.
Hence if we are able to find the density of a unit cell, it can be said that we have found the density of the cubic crystal itself. With this in mind, let us determine how to arrive at the density of a cubic crystal cell.
Now as we know a unit cell also has a cubic structure. It has one, two or four atoms located at various lattice points. Now with the help of geometry, some basic calculations and certain attributes of this cubic structure we can find the density of a unit cell. Let us start with the basic formula for the density of any solid. This formula is
Density = Mass/ Volume
The density of a Unit Cell will be
D = Mass of Unit Cell / Volume of Unit Cell
Mass of a Unit Cell
Now to calculate the mass of one unit cell we add up the mass of all the atoms contained in that particular cell. The number of atoms will depend on the kind of cell it is. So to obtain the mass of a unit cell we multiply the number of atoms “n” into the mass of each atom ”m”.
Mass of Unit Cell = m × n
But now the question remains, what is the mass of an atom? Well, this can be represented in terms of its Avogadro Number (NA)., i.e. number of units in one mole of any substance and the molar mass of an atom. So the mass of an atom can be calculated as
Mass of an Atom = 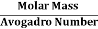
Mass of an Atom = 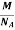
So now the formula for Mass of Unit Cell is as follows
Mass of Unit Cell = n × 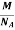
Volume of Unit Cell
As we already know, the unit cell is a cubic structure. So the Volume of a cube is the cube of the length of the side, Assume that the length of the side of the cube is “a”.
Volume of Unit Cell = a3
Density of Unit Cell
And now we finally arrive at the actual formula for the density of a unit cell
Density of a Unit Cell = 
Density of a Unit Cell = 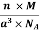
Example: An atomic solid crystallizes in a body center cubic lattice and the inner surface of the atoms at the adjacent corner are separated by 60.3 pm. If the atomic weight of A is 48, Find the density of the solid?
Solution:
According to given condition,
0.13 a = 60.3 ⟹ a = 463.8
So Density = 
= 
= 1.75 g/cc
2.2.4 SYMMETRY ELEMENTS (AXIS, CENTER AND PLANE)
Crystal symmetry describes the similarity in the lattice points and environment throughout the Crystal. Symmetry operation is that which transform the Crystal to itself. Simply a symmetry operation interchanges the position of atoms which results the same appearance of crystal.
The symmetry operations are translation, rotation, reflection and inversion. There are total 230 space groups of entire crystal system and 32 point group which describe all symmetry operation about a point in space with does not move during operation
It is a physical operation that changes the positions of the lattice points at exactly the same places after and before the operation.
In other words, it is an operation when applied to an object leaves it apparently unchanged. e.g.
There are two groups of symmetry operations represented by:
a)The point groups: Symmetry operations performed about a point or a line are called point group symmetry operations.
b) The space groups: symmetry operations perform by translation vectors are called space symmetry operations.
Translational Symmetry
A translational symmetry is occurred, for example, when the function sinx has a translation through an interval x = 2 leaves it apparently unchanged.
Inversion Symmetry
A center of symmetry: A point at the center of the molecule.(x,y,z)  (-x,-y,-z).
(-x,-y,-z).
The inversion operation is the imaginary operation of taking each point of the object through its center and out to an equal distance on the other side. However the net effect is to replace .(x,y,z)  (-x,-y,-z). And the crystal appears exactly the same.
(-x,-y,-z). And the crystal appears exactly the same.

Figure 21: Inversion Center
Center of inversion can only be in a molecule. It is not necessary to have an atom in the center (benzene, ethane). Tetrahedral, triangles, pentagons don't have a center of inversion symmetry. All Bravais lattices are inversion symmetric.
Reflection Symmetry
If the lattice have a plane or line in two dimensional which divide the lattice into two halves which are mirror image of each other then this is called reflection symmetry such a plane is symbolically represented by letter small m.
A plane in a cell such that, when a mirror reflection in this plane is performed, the cell remains invariant. Triclinic has no reflection plane. Monoclinic has one plane midway between and parallel to the bases, and so forth.
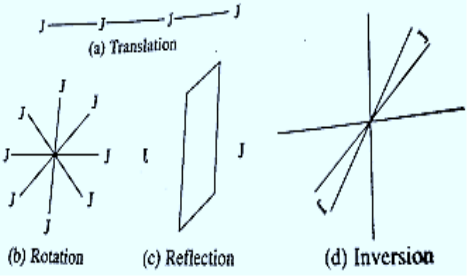
Figure 22: Symmetry operation
Rotational Symmetry
If a crystal is rotated through a point by an angle θ, it transforms the lattice to another lattice which is again itself in appearance. For simplest example is the crystal lattice is rotated by an angle θ is 3600 its lattice arrangement remains same.Possible value of n are 1,2,3,4,6 only multiplicity of rotational axis. Lattice can be found as one, two, three, four and six fold rotation about an axis which carries the lattice to itself. n=5,7,9 not possible and lattice cannot transform into itself under such rotation thus 5,7,9 fold symmetry are not possible.
We cannot find a lattice that goes into itself under other rotations. A single molecule can have any degree of rotational symmetry, but an infinite periodic lattice cannot.
2.2.5 BRAGG’S LAW
Consider a set of parallel planes called Bragg’s planes. Each atom is acting as a scattering center. The intensity of the reflected beam at certain angles will be maximum when the path difference between two reflected waves from two adjacent planes is an integral multiple of λ.

Figure 23: Bragg’s Law
Let ‘d’ be the distance between two adjacent planes, 'λ’ be the wavelength of the incident x-ray, ‘θ’ be the glancing angle.
The path difference between the rays reflected at A & B is given by
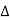 = CB + BD= d sinθ + d sinθ = 2dsinθ
= CB + BD= d sinθ + d sinθ = 2dsinθ
If the two consecutive planes scatter waves in phase with each other, then the path difference must be an integral multiple of wavelength.
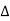 = nλ
= nλ
For the reflected light intensity to be maximum, the path difference
nλ= 2dsinθ
Where ‘n’ is the order of scattering.
This is called Bragg’s law
Therefore, Bragg’s law states that X-rays diffracted from different parallel planes of a crystal interfere constructively when the path difference is integral multiples of wavelength of X-rays.
From Bragg’s law nλ = 2d sin θ, since maximum possible value for sin θ is 1,
nλ/2d ≤ 1 or λ ≤ 2d.
This sets the limitation on the wavelength, i.e. in order to get the diffraction pattern by a crystal, the wavelength of X-rays should not exceed twice the inter-planar spacing.
Importance of Bragg’s law:
1. Bragg’s law is the essential condition to be satisfied by crystal planes in order to get diffraction pattern from a crystal.
2. It is used to calculate inter-planar spacing. Knowing the values of inter-planar spacing, lattice parameters can be determined.
Key Takeaways
- Packing Fraction =

- Packing efficiency (PE) is that fraction of the unit cell volume that is actually occupied by particles, not void space. Thus, the packing efficiency of a unit cell is
- These empty spaces are known as the interstitial voids, interstices or holes. The above voids in solids depend on the number of spheres.
- There are two types of interstitial voids in a 3D structure:
- Density of a Unit Cell =

- Symmetry operation interchanges the position of atoms which results the same appearance of crystal.
- There are two groups of symmetry operations represented by: a)The point groups: Symmetry operations performed about a point or a line are called point group symmetry operations. b) The space groups: symmetry operations perform by translation vectors are called space symmetry operations.
- Therefore, Bragg’s law states that X-rays diffracted from different parallel planes of a crystal interfere constructively when the path difference is integral multiples of wavelength of X-rays. It is given as nλ= 2dsinθ
- Bragg’s law is the essential condition to be satisfied by crystal planes in order to get diffraction pattern from a crystal.
2.3.1 MILLER INDICES
When dealing with crystalline materials, it often becomes necessary to specify a particular point within a unit cell, a crystallographic direction, or some crystallographic plane of atoms.
Labelling conventions have been established in which three numbers or indices are used to designate point locations, directions, and planes. The basis for determining index values is the unit cell, with a right-handed coordinate system consisting of three (x, y, and z) axes situated at one of the corners and coinciding with the unit cell edges.
For some crystal systems—namely, hexagonal, rhombohedral, monoclinic, and triclinic-the three axes are not mutually perpendicular, as in the familiar Cartesian coordinate scheme. A crystallographic direction is defined as a line between two points, or a vector.
The following steps are utilized in the determination of the three directional indices:
1. A vector of convenient length is positioned such that it passes through the origin of the coordinate system. Any vector may be translated throughout the crystal lattice without alteration, if parallelism is maintained.
2. The length of the vector projection on each of the three axes is determined; these are measured in terms of the unit cell dimensions a, b, and c.
3. These three numbers are multiplied or divided by a common factor to reduce them to the smallest integer values.
4. The three indices, not separated by commas, are enclosed in square brackets, thus: [hkl]. The h, k, and l integers correspond to the reduced projections along the x, y, and z axes, respectively.
Crystal planes are defined as some imaginary planes inside a crystal in which large concentration of atoms are present. Inside the crystal, there exists certain direction along which large concentration of atoms exists. These directions are called crystal directions.
Miller Indices are a method of describing the orientation of a plane or set of planes within a lattice in relation to the unit cell. They were developed by William Hallowes Miller.
Crystal planes and directions can be represented by a set of three small integers called Miller indices [because Miller derived a method of representing crystal planes]. These integers are represented in general as h, k and l. If these integers are enclosed in round brackets as (hkl), then it represents a plane. On the other hand, if they are enclosed in square brackets as [hkl], then it represents crystal direction perpendicular to the above-said plane.
Procedure for drawing the given plane having Miller indices (hkl)
1. A unit cell is drawn with the given lattice parameters. After taking any convenient point as the origin O, the OX, OY and OZ crystallographic axes are to be marked. If lattice parameters are not given, then unit cubic cell of arbitrary lattice constant will be taken.
2. The reciprocals of the Miller indices 1/h, 1/k, 1/l are to be taken. These values provide the intercepts of the given plane on OX, OY and OZ axes, respectively.
3. The intercepts are marked in the unit cell and the plane is drawn.
4. If the intercept is 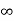 on any axis, the plane drawn will be parallel to that axis.
on any axis, the plane drawn will be parallel to that axis.
Example:
- The (111) surface
Intercepts: a , a , a
Fractional intercepts: 1 , 1 , 1
Miller Indices: (111)
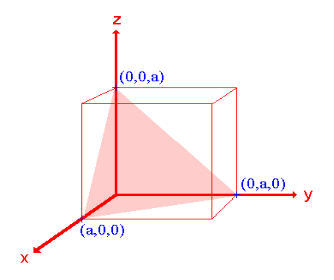 |
Figure 24: The (111) surface
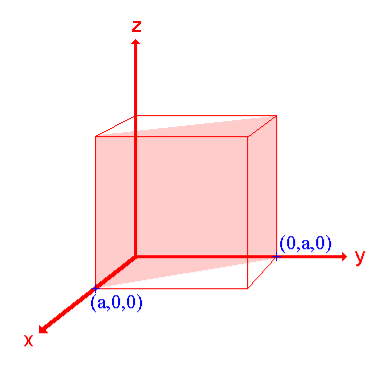
Ii. The (110) surface
Intercepts: a , a , ∞
Fractional intercepts: 1 , 1 , ∞
Miller Indices: (110)
 |
|
Figure 25: The (110) surface
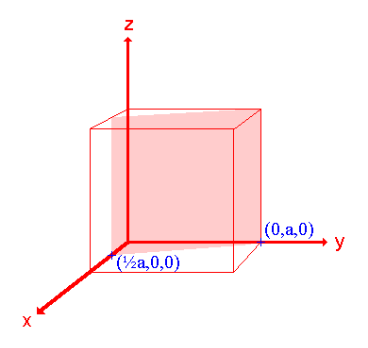
Iii. The (210) surface
Intercepts: ½a , a , 
Fractional intercepts: ½ , 1 , 
Miller Indices: (210)
 |
|
Figure 26: The (210) surface
Table
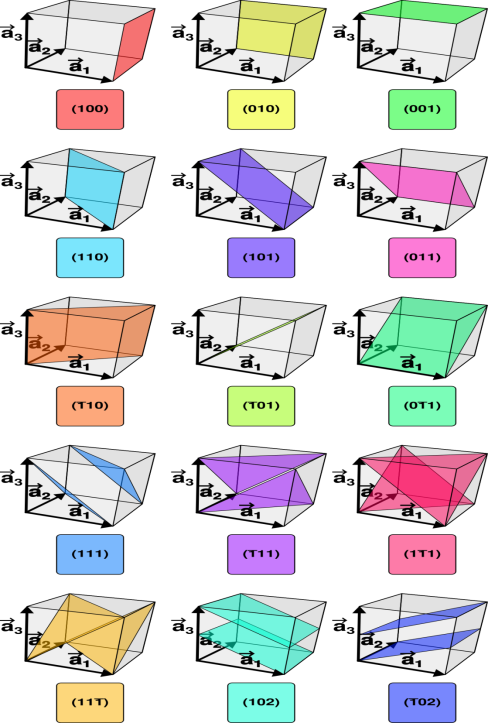
Figure 27: miller planes
2.3.2 INTER PLANNER DISTANCE (BY USING MILLER INDICES)
Distance of separation between successive hkl planes
The separation between successive parallel planes in rectangular axes crystal system can be extracted easily.
Consider a plane ABC which belongs to a family of planes. h, k, l are the Miller indices of this plane, which represents the set of planes. The perpendicular ON from the origin O to the plane represents the inter-planar spacing d = ON of this family of planes. Let ON make an angle α’, β’, γ’ with the x, y, z axes respectively.
The intercepts of the plane on the three axes are OA= a/h; OB= a/k; OC=a/l Where ‘a’ is the length of the cube edge. Then from figure, we have

Figure 28: Distance of separation between successive hkl planes
Cos =
= 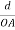 =
=  =
= 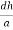
Cos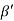 =
= 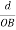 =
= 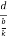 =
= 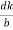
Cos =
=  =
= 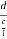 =
= 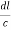
From the figure ON = 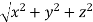
d = 
But, 
Substituting the values of cos’, cos’, cos’ in equation (2), We get,
For the orthogonal coordinates Substituting the values of cos’, cos’, cos’ in equation (2), We get,
(  )2 + (
)2 + ( 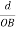 )2 +(
)2 +( 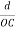 )2 = 1
)2 = 1
( )2 + (
)2 + (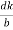 )2 +(
)2 +(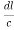 )2 = 1
)2 = 1
( ) (
) (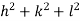 ) = 1
) = 1
d = 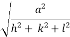
d = 
Key Takeaways
- Crystal planes are defined as some imaginary planes inside a crystal in which large concentration of atoms are present.
- Inside the crystal, there exists certain direction along which large concentration of atoms exists. These directions are called crystal directions.
- Miller Indices are a method of describing the orientation of a plane or set of planes within a lattice in relation to the unit cell.
- Distance of separation between successive hkl planes is given by d =

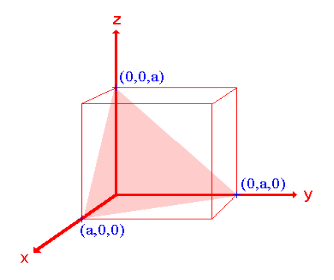
Q 1) Sketch the following planes of a cubic unit cell: (111) and (210)
Solution:
- The (111) surface
Intercepts: a , a , a
Fractional intercepts: 1 , 1 , 1
Miller Indices: (111)
 |
|
|
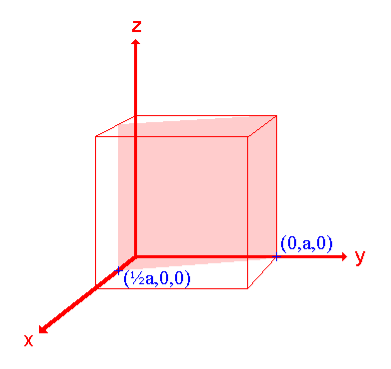
Ii. The (210) surface
Intercepts: ½a , a , 
Fractional intercepts: ½ , 1 , 
Miller Indices: (210)
 |
|
Q 2) An atomic solid crystallizes in a body center cubic lattice and the inner surface of the atoms at the adjacent corner are separated by 60.3 pm. If the atomic weight of A is 48, Find the density of the solid?
Solution:
According to given condition,
0.13 a = 60.3 ⟹ a = 463.8
So Density = 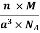
= 
= 1.75 g/cc
Q 3) In a diffractometer, X-rays with a wavelength of 0.1315 nm were used to produce a diffraction pattern for copper. The first order diffraction (n = 1) occurred at an angle θ = 25.25°. Determine the spacing between the diffracting planes in copper.
A 14)
The distance between the planes is found by solving the Bragg equation,
nλ = 2d sin θ,
For d.
This gives: d=nλ2sinθ
=1(0.1315nm)2sin(25.25∘)=0.154nm
Reference
- Solid State Physics, S.O. Pillai, McGraw Hill Publications
- Engineering Physics, R.K. Gaur and S.L. Gupta, Dhanapat Rai Publications
- A Text Book of Engineering Physics, M.N. Avadhanulu, P.G. Kshirsagar, S. Chand and Company Ltd.