UNIT4 | unit 4 relativistic mechanics

PHY

UNIT-4

RELATIVISTIC MECHANICS

4.1 INTRODUCTION, POSTULATES OF SPECIAL THEORY OF RELATIVITY, LORENTZ TRANSFORMATION OF SPACE AND TIME

4.1.1 INTRODUCTION

Mechanics is that branch of science which deals with the motion of particles. In order to describe the motion of a particle a coordinate system is required. The choice of coordinate system depends upon the nature of the problem. But generally motion is studied in a coordinate system attached to the earth. Since the earth is rotating about its axis and also about the sun, the coordinate system attached to it is an accelerated system.

A frame of reference is a set of coordinates (for example x, y & z axes) with respect to whom any physical quantity can be determined.

A “frame of reference” is just a set of coordinates; we use to measure positions, velocities and time.

A point in space is specified by its three coordinates (x, y, z) and an “event” like a little explosion specified by a place and time: (x, y, z, t).

Figure 1: Frame of reference

INERTIAL & NON-INERTIAL FRAMES

Inertial frames of reference

The inertia of a body is the resistance of changing its state of motion.

Uniformly moving reference frames (e.g. Those considered at 'rest' or moving with constant velocity in a straight line) are called inertial reference frames.

An inertial frame is defined as one in which Newton’s law of inertia holds that is anybody which isn’t being acted on by an outside force stays at rest if it is initially at rest, or continues to move at a constant velocity if that’s what it was doing to begin with.

Special relativity deals only with physics viewed from inertial reference frames.

If we can neglect the effect of the earth’s rotations, a frame of reference fixed in the earth is an inertial reference frame.

An example of a non-inertial frame is a rotating frame such as a carousel.

Let us understand it by an example; suppose a body is kept on the surface of the earth, for a person on earth it is at rest while for a person on the moon it is in motion so what is my inertial frame here?

Actually, the term inertial frame is relative i.e. first we assume a reference frame to be the inertial frame of reference. So a more general definition of an inertial frame would be: Inertial frame is at rest or moves with constant velocity with respect to my assumed inertial reference frame.

Non-inertial frame of reference

A frame that is accelerated with respect to the assumed inertial frame of reference. Newton’s law will not hold true in these frames.

So in the above example if I assume earth to be an inertial reference frame then moon becomes a non-inertial reference frame as it is in accelerated motion with respect to earth. But if we want to make Newton’s law hold here we need to take some mysterious forces also known as pseudo forces.

4.1.2 POSTULATES OF SPECIAL THEORY OF RELATIVITY

Einstein gave two postulates to explain the negative result of Michelson-Morley experiment. They form the basis of the special theory of relativity. These postulates are:

The laws of physics take the same form in all inertial frames.

According to first postulate all inertial frames are equivalent. It is meaningless to talk of absolute motion. Only the motion relative to frame of reference has any physical meaning.

The velocity of light in vacuum has the same value c and is independent of the relative velocity of the source and the observer.

The second postulate simply expresses the result of Michelson Morley experiment.

Consequences of Postulates of Relativity

The first postulate requires that Maxwell equations should be valid in all inertial frames. But we know that these equations are not Galilean invariant. Thus postulate 1 rejects the validity of the Galilean transformation.

There must be some other transformation under which Maxwell's equations are invariant. But Newton's laws are Galilean invariant and cannot be invariant under the transformation which makes Maxwell's equations invariant. This means that laws of Newtonian mechanics are not really valid. We must have a new set of mechanical laws which together with Maxwell equations are invariant under a new transformation which is not Galilean.

This requires a revision of the fundamental concepts of space and time. These are the absolute quantities in Newtonian mechanics. The absoluteness of these quantities need to be discarded in order to preserve the Einstein postulates which are necessary to explain the negative result of Michelson Morley experiment. The new transformation to replace the Galilean transformation was first derived by H.A. Lorentz in the year 1890 and is known as the Lorentz transformation.

Postulate 2 explains the negative result of the Michelson-Morley experiment. This postulate implies that the velocity of light is unaffected by the ether wind and is c for both the beams. Thus there is no path difference between the two beams and there is no question of any fringe shift. Moreover this hypothesis renders the ether hypothesis redundant,

Thus we need a transformation between two inertial frames which

(a) Preserves the velocity of light

(b) Keeps the forms of laws of physics invariant.

Key Takeaways

Einstein gave two postulates to explain the negative result of Michelson-Morley experiment.
They form the basis of the special theory of relativity.
These postulates are: (i)The laws of physics take the same form in all inertial frames. (ii) The velocity of light in vacuum has the same value c and is independent of the relative velocity of the source and the observer.

4.1.3 LORENTZ TRANSFORMATION OF SPACE AND TIME

Galilean transformations

Galilean Coordinate Transformations: For simplicity: - Let coordinates in both references equal at (t = 0). Use Cartesian coordinate systems.

Newton’s laws are only applicable at inertial reference frames. According to Galilean transformations, Newton’s laws are invariant at any inertial reference frame. In other words, the mechanical movement of a particle is exactly the same at two different reference frames, If both of them are inertial (i.e. one moves with constant velocity w.r.t the other & vice versa).

There is no mechanical experiment by which one can distinguish whether a system is at rest or is moving with a constant speed in a straight line (Galilean relativity).

Suppose we know from experiment that these laws of mechanics are true in one frame of reference. How do they look in another frame, moving with respect to the first frame?

To find out, we have to figure out how to get from position, velocity and acceleration in one frame to the corresponding quantities in the second frame.

Obviously, the two frames must have a constant relative velocity, otherwise the law of inertia won’t hold in both of them. Let’s choose the coordinates so that this velocity is along the x-axis of both of them.

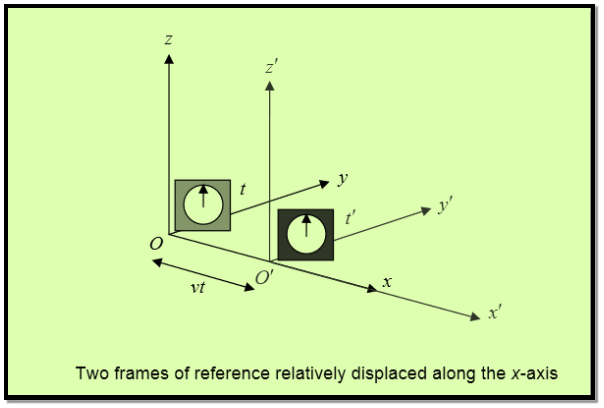
Figure 2: Frame of reference relatively displaced along the x-axis

Notice we also throw in a clock with each frame. Suppose S′ is moving relative to S at speed v along the x-axis. For convenience, let us label the moment when O′ passes O as the zero point of timekeeping. That mean at t=0 O and O’ coincide with each other.

Now let us try to find the coordinates of the event (x, y, z, t) in S′

It’s easy to see t′ = t

We synchronized the clocks when O′ passed O. Also, evidently, y′ = y and z′ = z, from the figure.

We can also see that x = x′ +vt.

Thus (x, y, z, t) in S corresponds to (x′, y′, z′, t′) in S′, where

x = x′ +vt.

y = y’

z = z’

t =t’

That’s how positions transform; these are known as the Galilean Transformations.

Velocity

The velocity in S′ in the x′ direction is given by u’x

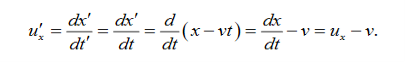
This is obvious anyway it’s just the addition of velocities formula.

ux = u’x +v

Acceleration

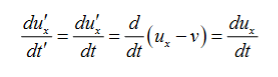
Since v is constant. That is to say,

a’x =ax

The acceleration is the same in both frames. This again is obvious as the acceleration is the rate of change of velocity, and the velocities of the same particle measured in the two frames differ by a constant factor-the relative velocity of the two frames.

LORENTZ TRANSFORMATION

As discussed above we need a transformation between two inertial frames which

(a) Preserves the velocity of light

(b) Keeps the forms of laws of physics invariant.

Lorentz transformation is the relationship between two different coordinate frames that move at a constant velocity and are relative to each other. The name of the transformation comes from a Dutch physicist Hendrik Lorentz.

The Galilean transformation nevertheless violates Einstein’s postulates, because the velocity equations state that a pulse of light moving with speed c along the x-axis would travel at speed c−v in the other inertial frame.

Figure 3: Transformation of coordinates

Specifically, the spherical pulse has radius r=ct at time t in the unprimed frame, and also has radius r′=ct′ at time t' in the primed frame.

Expressing these relations in Cartesian coordinates gives

x2+y2+z2−c2t2 =0 ………..(1)

x′2+y′2+z′2−c2t′2=0 ………..(2)

The left-hand sides Equations and can be set equal because both are zero.

Because y=y′ and z=z′ so, we obtain

x2−c2t2 =x′2−c2t′2 ………..(3)

However, this cannot be satisfied for nonzero relative velocity v of the two frames if we assume the Galilean transformation results in t=t′ with x=x′+vt′.

To find the correct set of transformation equations, assume the two coordinate systems S and S′

The laws of mechanics are invariant under Galilean transformations, whereas electrodynamics and Maxwell’s equations are varying under this transformation. This shows that the velocity of light will have different values for different observers moving with different uniform velocities. But the speed of light is invariant in all inertial frames of reference; hence, Galilean transformations need to be modified.

Lorentz deduced the transformation equations, which are in agreement with the results of Michelson–Morley experiment. The Lorentz transformations are deduced as given below.

Lorentz transformation equations are developed. Let x, y, z and t be the space and time coordinate in rest system or standard system. The system with x', y', z' moves with velocity 'v' along the x-axis.

The origins at t=t'=0 coincide. The most general transformation equations relating the coordinates of an event in two systems can be written as,

x’ = Ax +Bt ………..(4)

y’ = y ………..(5)

z’ = z ………..(6)

t’ = Cx +Dt ………..(7)

Figure 4: Transformation of coordinates

The transformations are linear.

If they are not linear one system would predict acceleration while in other system velocity was even constant.

Because of symmetry, y' and z' axes are left unchanged by the transformation.

Constant can be calculated by using the following boundary conditions.

Observers in S and S' see (O') the origin of S' as

x = vt

x’ = 0

Substituting values of x and x' in equation (4) We get

0 = Avt +Bt

i.e. B =- Av ………..(8)

Observer in S' and S see the origin (O) of S as

x' = vt

x = 0

Substituting values of x and x' in equation (4) we get

-vt’ =Bt ………..(9)

Substituting the value of B from equation (8), we get

-vt’ =- Avt ………..(10)

In equation (7) put x=0 we get

t’ = Dt

So equation (10) become

-v Dt =- Avt

A =D ………..(11)

A light pulse is sent out from the origin of S towards x at t=0, its location is given by

x= ct

x’ = ct’

Substituting values of x and x' in equation (4), we get

Ct’ = Act +Bt

Substituting the value of B from equation (8), we get

Ct’ = Act +(- Avt) ………..(12)

Substituting values of x and D from eq no (11) in eq no.(7) , we get

t’ = Cct +At

Substituting above value of t' in eq no.(12) , we get

c(Cct +At) = Act - Avt

Cc2t +Act =Act - Avt

Cc2t =Avt

C =-A 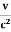………..(13)

A light pulse is emitted along y axis in S system at t=0, its coordinate in both systems are

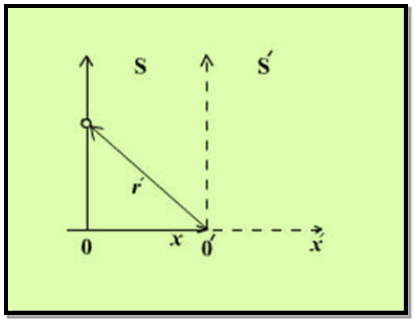
Figure 5: Frame S and S’

y= ct, x=0

r’=ct’ where

Using equation (5)

r’2 = x’2+y’2

Using equation (5)

y’= y= ct

And from equation (4) and (7)

x’ = Bt = -Avt

t’= Dt =-At

Therefore r’2 = x’2+y’2 become

c2t’2 = (-Avt)2 +(ct)2

Substituting value of t' above equation became

c2A2t2 = A2v2t2 +c2t2

(c2 - v2) A2t2 = c2t2

A2 =

A =

A = ………..(14)

Substituting the Values of A, B, C, D in equation (1) and (4)

So the Lorentz transformation equations would be,

x’= -

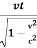
x’= (x-vt)

x’=(x-vt)

Where

And

t’ = - +

t’= ( t - )

Lorentz transformation equations therefore are

x’= (x - vt)

y’ =y

z’ = z

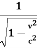t’= ( t - )

Or these can be written as

x’= (x-vt)

y’ =y

z’ = z

t’= ( t - )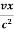

Where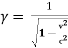

This set of equations, relating the position and time in the two inertial frames, is known as the Lorentz transformation. They are named in honour of H.A. Lorentz (1853–1928), who first proposed them. Interestingly, he justified the transformation on what was eventually discovered to be a fallacious hypothesis.

The reverse transformation expresses by the following equations. Simply interchanging the primed and unprimed variables and substituting gives:

x= 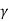(x’+ vt)

y =y’

z = z’

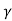t= (t’ + )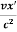

Key Takeaways

Thus (x, y, z, t) in S corresponds to (x′, y′, z′, t′) in S′, where x = x′ +vt, y = y’, z = z’, t =t’ these are known as the Galilean Transformations.
This set of equations, relating the position and time in the two inertial frames, is known as the Lorentz transformation.
Lorentz transformation are given as x’= 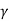(x-vt), y’ =y, z’ = z and t’= ( t - 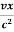) Where

4.2 LENGTH CONTRACTION, TIME DILATION

4.2.1 LENGTH CONTRACTION

Consider a frame S' moving with respect to S with a uniform speed v along x direction figure. Let the rod AB lie along the O'x' axis. The rod is at rest in the frame S' and its length as measured by an observer in S' shall be called the rest length of the rod. To calculate this length the observer in S' will measure the x' coordinates of the two ends A and B. These coordinates shall be independent of the time of observation. If x1' and x2' are the x' coordinates of two ends A and B then the rest length l0 of the rod is

l0 = x'2 – x'1

In the coordinate system S the x coordinates of ends A and B will change with time. In order to measure the length of the rod, the observer in S will have to measure simultaneously the coordinates of the ends A and B. If x1 and x2 are the coordinates of ends A and B at the time of observation t then the length of rod as observed in frame S is

l= x2 – x1

Figure 6: Length Contraction

From Lorentz equations we have

x'2 = (x2 – v t)

x1' = 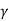(x1 – v t)

Subtracting these equations we obtain

x2' - x1' = (x2 — x1)

Using eq. (6.57) and (6.58) it becomes

l0 = 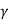l

I =

Since 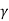is always greater than one, therefore

l < l0

Thus the length of the rod measured from the frame in which it is moving is smaller than its length in a frame in which it is at rest by a factor or 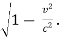Hence the length of a moving rod appears shortened by a factor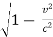

Example

Consider a rocket moving past the earth. Suppose it carries a meter stick oriented along the direction of motion of rocket. This stick will appear to be shortened by a factor to an observer at rest on the earth.

Note the following points

The length contraction is significant only if the speed of rod approaches the velocity of light.
The shortening of rod occurs only along the line of motion. The length of meter stick oriented perpendicular to the direction of motion is not changed.

4.2.2 TIME DILATION

Consider a frame S' moving with velocity v with respect to frame S along the x direction Fig (6.6). Suppose the clock is located in the system S' at the point x'. The clock is stationary with respect to S'. Let t1 ' and t2' are two instants of time recorded on this clock by an observer in S'. Then the interval of time as observed in S' is

∆t' = t2' – t1'

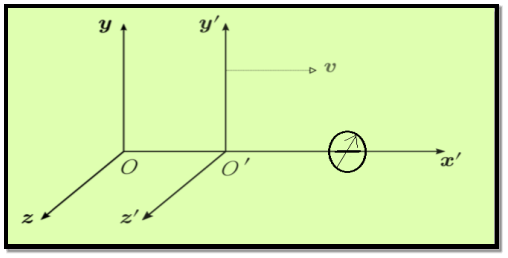
Figure 7: Time dilation

Now we wish to find how this time interval appears to an observer in S. This can be done by applying a Lorentz transformation from S' to S with the same value of x'. The transformation equation required is (6.51 d). From this we can write

t1 = (t1' + v x' / c2)

t2 = (t'2 + v x' / c2)

Subtracting eq. (6.64) from eq. (6.63) we obtain

∆t= t1 – t2 = 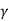(t1' – t2')

Using eq. (6.62) it becomes

∆t= t1 – t2 = 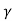(∆t')

Since > 1 so

∆t > ∆t'

This means that the time interval as observed in the moving frame of clock is greater than the One observed in the rest frame of the clock. We can express the same thing by saying that a moving clock appears to run slow. We often say that time has been dilated or lengthened in the moving observer frame. The time as observed by an observer moving with the clock is less than the one observed by a moving observer.

We highlight the following points

Time intervals are affected by relative motion.

 A stationary clock measures a longer time interval between events occurring in a moving frame of reference than does a clock in the moving frame.

Key Takeaways

The length contraction is given by l0 = l
The length contraction is significant only if the speed of rod approaches the velocity of light.
The shortening of rod occurs only along the line of motion.
Time dilation is given by ∆t= t1 – t2 = 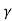(∆t')
Time intervals are affected by relative motion.

 A stationary clock measures a longer time interval between events occurring in a moving frame of reference than does a clock in the moving frame.

4.3 EQUIVALENCE OF MASS AND ENERGY

EINSTEIN’S MASS ENERGY RELATION

Mass-energy equivalence implies that even though the total mass of a system changes, the total energy and momentum remain constant. Consider the collision of an electron and a proton. It destroys the mass of both particles but generates a large amount of energy in the form of photons.

Einstein's Mass-energy Relation

Mass-energy equivalence states that every object possesses certain energy even in a stationary position.

A stationary body does not have kinetic energy. It only possesses potential energy and probable chemical and thermal energy.

According to the field of applied mechanics, the sum of all these energies is smaller than the product of the mass of the object and square of the speed of light.

Mass-energy equivalence means mass and energy are the same and can be converted into each other.

Einstein put this idea forth but he was not the first to bring this into the light. He described the relationship between mass and energy accurately using his theory of relativity. The equation is known as Einstein's mass-energy equation and is expressed as,

E = mc2

Where E= equivalent kinetic energy of the object.

The mass–energy equivalence gives the relation between the mass and energy.

Derivation of mass energy equation

We know that according to classical mechanics, the rate of change of momentum is proportional to force acting upon the body in the direction of motion.

F = 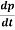= …...... (1)

According to the theory of relativity, mass and velocity are variable so equation (1) after become.

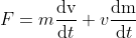$Description: https://latex.codecogs.com/gif.latex?F%3Dm%5Cfrac%7B%5Cmathrm%7Bdv%7D%20%7D%7B%5Cmathrm%7Bd%7D%20t%7D+v%20%5Cfrac%7B%5Cmathrm%7Bdm%7D%7D%7B%5Cmathrm%7Bd%7D%20t%7D$ …...... (2)

The force F acting on the body makes a displacement dx.

We know that work done dw is given by product of force and displacement

And also the work is stored as kinetic energy (dε) in the body. So work done can be written as

Dw = dε = Fdx ...........(3)

Substituting force F from Equation (2) in Equation (3). We get

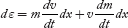
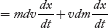
dε = mvdv + v2dm ...........(4)

And also velocity v =

The relativistic mass m is given by

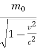= m

Squaring on both sides, we get

m2 = =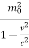

= ........... (5)

Differentiating Equation (5), we get

2mc2dm − 2mv2dm − 2m2vdv = 0

c2dm = v2dm + mvdv …........ (6)

Comparing Equations (4) and (6), we get

dε = c2dm ............(7)

By applying force, the mass of a body increases from m0 to m and hence the kinetic energy. The total energy acquired by the body is obtained by integrating Equation (7)

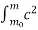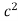
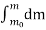ε = dm = = (m - m0) ............ (8)

Therefore increase in kinetic energy is due to the increase in mass of the body. The total energy (E) of the body is the sum of increase in kinetic energy of the body due to motion and the energy at rest (moc2):

∴ E = ε + moc2

Using Equation (8)

E = mc2 − moc2 + moc2 = mc2

E = mc2 …………. (9)

This shows that increase in energy equivalent to increase in mass. In other words anything that increase energy will increase its relativistic mass.

The above equation shows the equivalence between mass and energy also known as Einstein’s mass–energy relation.

Key Takeaways

Mass-energy equivalence states that every object possesses certain energy even in a stationary position.
A stationary body does not have kinetic energy. It only possesses potential energy and probable chemical and thermal energy.
The equation is known as Einstein's mass-energy equation and is expressed as E = mc2
The relativistic mass m is given by 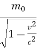= m
Increase in kinetic energy is due to the increase in mass of the body.

4.4 NUMERICAL PROBLEMS

Example: The Hypersonic Technology Vehicle 2 (HTV-2) is an experimental rocket vehicle capable of traveling at 21,000 km/h (5830 m/s). If an electronic clock in the HTV-2 measures a time interval of exactly 1-s duration, what would observers on Earth measure the time interval to be?

Solution:

Given

Δτ=1s

v=5830m/s.

Δt =?

We know ∆t= t1 – t2 = (∆t')

Δt=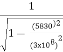 = 1.000000000189s

Example: A certain process requires 10-6 sec to occur in an atom at rest in laboratory. How much time will this process require to an observer in the laboratory? When the atom is moving with speed of 5 x107 m/sec.

Solution:

Given Δt = 10-6 sec

v = 5 x109 cm/sec

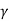∆t= (∆t')

∆t' = ∆t /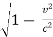

∆t' =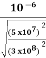 = 1.028 x 10-6 sec

Example: Calculate the time interval of the signal using Lorentz transformation when a spacecraft S’ is crossed by another spacecraft S at a speed of c/2 on their way to Alpha Centauri. When spacecraft S crosses S’, the captain of S’ sends a signal that lasts for 1.2s.What is the fine time interval of the single.

Solution:

Given:

Δt’ = t‘2−t‘1 = 1.2s

Δx’ = x‘2−x‘1 = 0

The time signal starts and ends at (x’, t‘1)

Using the first Lorentz transformation equation we get,

Δt = t2 – t1

Δx = x2 – x1

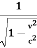Δt= ( t’ + )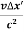

As the time interval of S’ is fixed, we can consider Δx’ = 0 and the time interval δt becomes:

Δt=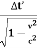

Substituting Δt’ = 1.2s we get

Δt=

Δt = 1.6s

Example: Compute the contracted length of an object whose initial length 10m and travel with a velocity 0.75c?
Solution:

Given parameters are,
L0 = 10m

v = 0.75c

c = Speed of light (3.0 x 108 m/s)

The formula for length contraction is

l0 = l

Or L0 = L

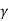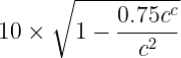
Description: Length Contraction Related Problems

L = 10 × √1- (0.75)2

L = 10 × √(o.438)

L = 6.618 m.

Example: A observer on earth sees a rocket zoom by at .95c. If the rocket is measured to be 5.5 m in length, how long is the rocket ship as measure by the astronaut inside the rocket?

Solution:

The formula for length contraction is

l0 = l