Unit - 1
ODE of First order and Degree and Application
Differential Equations (Definition) –
A differential equation is an equation involving an unknown function and
Its derivatives.
Ex. 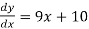
“A differential equation is an ordinary differential equationif the unknown function depends on only one independent variable.”
Notation:
The expression y’, y’’ , y’’’ …….yⁿ are used to represent derivatives.
Here, y’ =  , y’’ =
, y’’ = 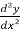 and so on.
and so on.
1st order linear differential equations-
A 1st order linear differential equations is linear when it is given in the form below-
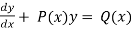 ,
,
Where P(x) and Q(x) are the functions of x
Here we will learn about degree and order of an ordinary differential equation.
Order:
The order is the highest derivative:
For example:
(1) 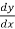 + y³ = 8x , here it has only first derivative so its ‘first order’.
+ y³ = 8x , here it has only first derivative so its ‘first order’.
(2) 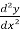 + y³ = 7x , here it has a second derivative so its ‘second order’ and so on.
+ y³ = 7x , here it has a second derivative so its ‘second order’ and so on.
Degree:
Degree is known as the exponent of higher derivative.
For example:
1. 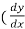 )² + y³ = 8x, here its highest derivative has an exponent of 2, it is a first order second degree ordinary differential equation.
)² + y³ = 8x, here its highest derivative has an exponent of 2, it is a first order second degree ordinary differential equation.
2. 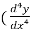 ) +
) +  y³ = 8x, here in this example its higher derivative has no exponent, so we can say that this is the third order and first degree ordinary differential equation.
y³ = 8x, here in this example its higher derivative has no exponent, so we can say that this is the third order and first degree ordinary differential equation.
Note-
- A solution to a differential equation which contains one or more arbitrary constants of integration is called general solution.
- If additional information is given so that constant may be calculated the particular solution additional information are boundary conditions.
Formation of differential equations
We can form a differential equation by differentiating the ordinary equation and eliminating the arbitrary constant.
Example: From the differential equation by eliminating arbitrary constant.
y = A cos x + B sin x
Sol. Differentiate the given equation,
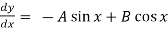 -----------------(1)
-----------------(1)
Now, we will differentiate equation (1) again,
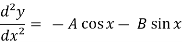
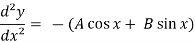
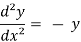
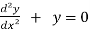 ans.
ans.
Example: From the differential equation by eliminating arbitrary constant.
y² = Ax² + Bx² + C
Sol.
We will differentiate the given function, we get

Again differentiate,
 + 2
+ 2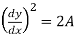
On differentiating again, we get
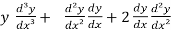 = 0
= 0
Example: Obtain the differential equation of 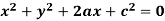 here c is a constant and ‘a’ is a variable.
here c is a constant and ‘a’ is a variable.
Sol.
Here we have,
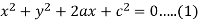
Differentiate with respect to ‘x’, we get-
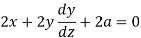
Or
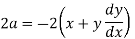
Put this value in (1),
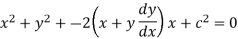
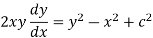
Which is the required DE.
General and particular solutions
A relation between the variables which satisfies the given DE, is called the solution of that DE.
General solution-
The general solution of a DE is that in which the number of arbitrary constants is equals to the order of DE. General solution is also called complete solution.
Particular solution-
A particular solution is that which can be obtained from the general solution by giving particular values to the arbitrary constants.
Let’s understand how to solve differential equations:
(1) The solution of equations of the form 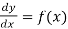
This type of equation can be solved by direction integration:
Y = 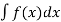
Example: Find the general solution of x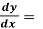 2 – 4x³
2 – 4x³
Solution: rearranging the given equation:
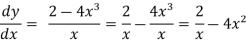
On integrating both sides,
y = 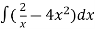 = 2 In x -
= 2 In x - 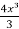 + c
+ c
This is the general solution.
Example: Find the particular solution of the differential equation 5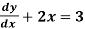 , given the boundary condition y = 1
, given the boundary condition y = 1 , when x = 2.
, when x = 2.
Solution:
Rearrange the diff. Equation,
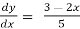 =
=  -
- 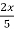
y = 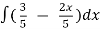 =
=  -
- 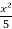 + c, which is the general solution.
+ c, which is the general solution.
Put the boundary conditions to find c,
1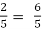 -
- 
Which gives, c = 1
Hence the particular solution is,
y = 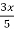 -
- 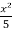 + 1.
+ 1.
(2) The solution of equation of the form 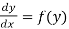 ,
,
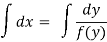
Example: Find the general solution of 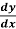 = 3 + 2y
= 3 + 2y
Solution: here, 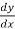 = 3 + 2y gives,
= 3 + 2y gives,
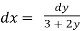 ,
,
Integrating both sides,
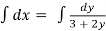 ,
,
By substitution, u = (3 +2y),
X =  In(3 + 2y) + c.
In(3 + 2y) + c.
Example: Determine the particular solution of (y² - 1)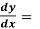 3y given that y =1 when x = 2
3y given that y =1 when x = 2 .
.
Solution: It gives,
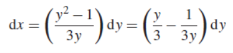
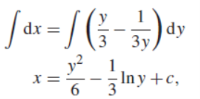
When putting the values, y =1 ,x = 2 ,
,
The particular solution will be,
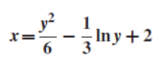
(3) The solution of equation of the form 
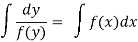
Example-1: Solve the equation 4xy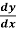 = y² - 1
= y² - 1
Solution: on separating variables, we get
(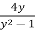 ) dy =
) dy = dx
dx
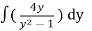 =
= 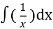
Using substitution, u = y² - 1
2In(y² - 1) = In x + c.
Example-2: Determine the particular solution of 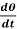 = 2
= 2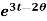 , given that t = 0, when θ = 0
, given that t = 0, when θ = 0
Solution: 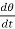 = 2
= 2 = 2
= 2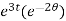 ,
,
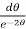 = 2
= 2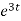 dt
dt
 dθ =
dθ = 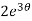 dt
dt
Now integrating both sides,
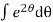 =
= 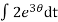
The general solution is ,
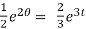 + c.
+ c.
When t = 0 and θ = 0, c =
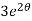 =
= 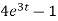
Key takeaways:
- “A differential equation is an ordinary differential equationif the unknown function depends on only one independent variable.”
- The order is the highest derivative:
- Degree is known as the exponent of higher derivative.
- A solution to a differential equation which contains one or more arbitrary constants of integration is called general solution.
- A relation between the variables which satisfies the given DE, is called the solution of that DE.
Exact differential equations
Definition-
An exact differential equation is formed by differentiating its solution directly without any other process,
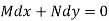
Is called an exact differential equation if it satisfies the following condition-
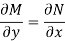
Here 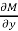 is the differential co-efficient of M with respect to y keeping x constant and
is the differential co-efficient of M with respect to y keeping x constant and 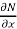 is the differential co-efficient of N with respect to x keeping y constant.
is the differential co-efficient of N with respect to x keeping y constant.
Step by step method to solve an exact differential equation-
1. Integrate M w.r.t. x keeping y constant.
2. Integrate with respect to y, those terms of N which do not contain x.
3. Add the above two results as below-

Provided 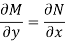
Example-1: Solve 
Sol.
Here M = 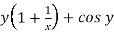 and N =
and N = 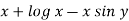

Then the equation is exact and its solution is-
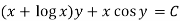
Example-2: Solve-
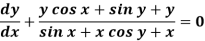
Sol. We can write the equation as below-
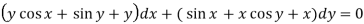
Here M =  and N =
and N = 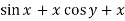
So that-
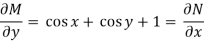
The equation is exact and its solution will be-

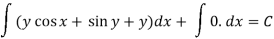
Or
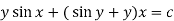
Example-3: Determine whether the differential function ydx –xdy = 0 is exact or not.
Solution. Here the equation is the form of M(x , y)dx + N(x , y)dy = 0
But, we will check for exactness,
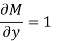
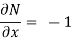
These are not equal results, so we can say that the given diff. Eq. Is not exact.
Example: Solve-

Sol.
Here, M = 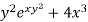 and N =
and N = 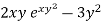
So that-
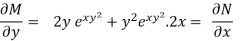
Thus the equation is exact and its solution is-
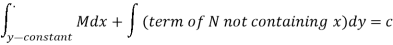
Which means-
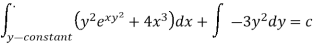
Or
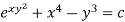
Key takeaways-
- The necessary condition for exactness-
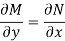
2. 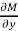 is the differential co-efficient of M with respect to y keeping x constant
is the differential co-efficient of M with respect to y keeping x constant
3. 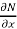 is the differential co-efficient of N with respect to x keeping y constant
is the differential co-efficient of N with respect to x keeping y constant
Reducible to Exact differential equations
Equation reducible to exact form-
1. If M dx + N dy = 0 be an homogenous equation in x and y, then 1/ (Mx + Ny) is an integrating factor (M dx + N dy 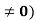
Example: Solve-

Sol.
We can write the given equation as-

Here,
M = 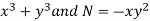
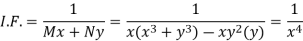
Multiply equation (1) by 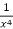 we get-
we get-


This is an exact differential equation-
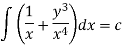
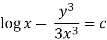
Example: Solve-
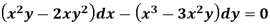
Sol.
The equation given is homogeneous in x and y-
Now, the integrating factor is-

Multiply by 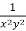 , the equation reduces to-
, the equation reduces to-
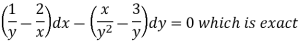
Now the solution is-
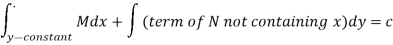
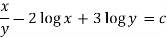
2. I.F. For an equation of the type 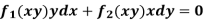
IF the equation Mdx + Ndy = 0 be this form, then 1/(Mx – Ny) is an integrating factor.
Example: Solve-
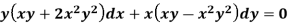
Sol.
Here we have-
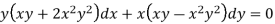
Now divide by xy, we get-
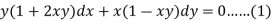
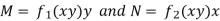

Multiply (1) by 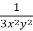 , we get-
, we get-
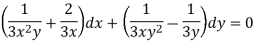
Which is an exact differential equation-
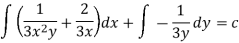
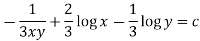
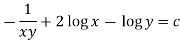
3. In the equation M dx + N dy = 0,
(i) If  be a function of x only = f(x), then
be a function of x only = f(x), then 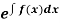 is an integrating factor.
is an integrating factor.
(ii) If 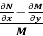 be a function of y only = F(x), then
be a function of y only = F(x), then 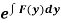 is an integrating factor.
is an integrating factor.
Example: Solve-
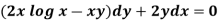
Sol.
Here given,
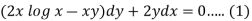
M = 2y and N = 2x log x - xy
Then-
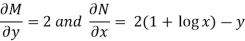
Here,
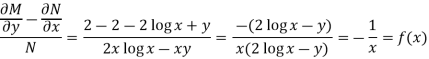
Then,

Now multiplying equation (1) by 1/x, we get-
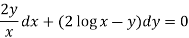
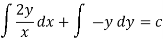
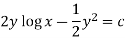
4. For the following type of equation-
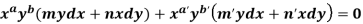
An I.F. Is 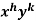
Where-

Example: Solve-
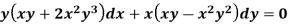
Sol.
We can write the equation as below-
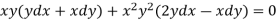
Now comparing with-
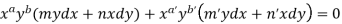
We get-
a = b = 1, m = n = 1, a’ = b’ = 2, m’ = 2, n’ = -1
I.F. = 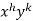
Where-
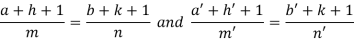
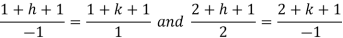
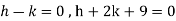
On solving we get-
h = k = -3

Multiply the equation by 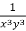 , we get-
, we get-
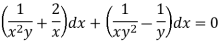
It is an exact equation.
So that the solution is-
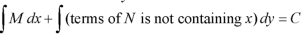
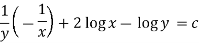
Linear differential equations
A differential equation of the form
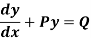
Is called linear differential equation.
This is the standard form of a linear differential equation.
It is also called Leibnitz’s linear equation.
Here P and Q are the function of x
Note-
A differential equation is said to be linear if the dependent variable and differentia coefficient occur only in the first degree and not multiplied together.
Working rule
(1) Convert the equation to the standard form 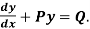
(2) Find the integrating factor.
(3) Then the solution will be y(I.F) = 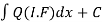
Where integrating factor (I.F.) is = 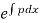
Example-1: Solve-
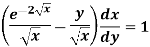
Sol. We can write the given equation as-

So that-
I.F. = 
The solution of equation (1) will be-
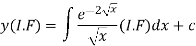
Or
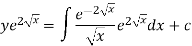
Or
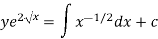
Or
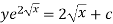
Example-2: Solve-
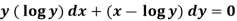
Sol.
We can write the equation as-
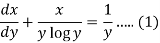
We see that it is a Leibnitz’s equation in x-
So that-
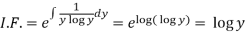
Therefore the solution of equation (1) will be-
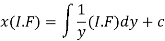
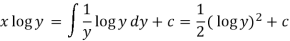
Or
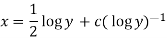
Example-3: Solve sin x 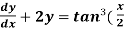 )
)
Solution: here we have,
Sin x 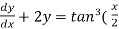 )
)
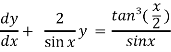
Which is the linear form,
Now,
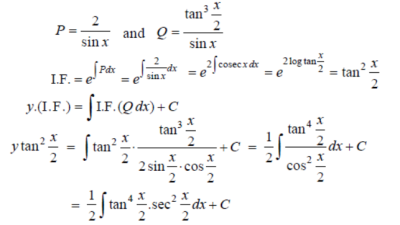
Put tan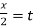 so that
so that  sec²
sec²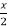 dx = dt, we get
dx = dt, we get
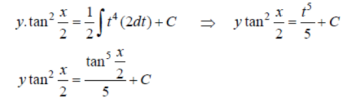
Which is the required solution.
Key takeaways-
- The form a linear differential equation-
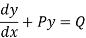
2. A differential equation is said to be linear if the dependent variable and differentia coefficient occur only in the first degree and not multiplied together
3. I.F. = 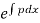
Reducible to Linear differential equations
Bernoulli’s equation-
The equation
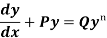
Is reducible to the Leibnitz’s linear equation and is usually called Bernoulli’s equation.
Working procedure to solve the Bernoulli’s linear equation-
Divide both sides of the equation –
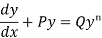
By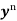 , so that
, so that
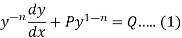
Put 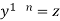 so that
so that 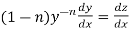
Then equation (1) becomes-
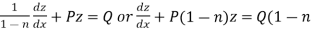 )
)
Here we see that it is a Leibnitz’s linear equations which can be solved easily.
Example: Solve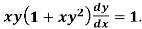
Sol.
We can write the equation as-
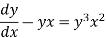
On dividing by 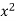 , we get-
, we get-

Put 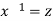 so that
so that 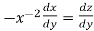
Equation (1) becomes,
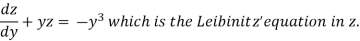
Here,
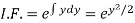
Therefore the solution is-
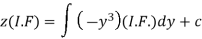
Or
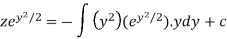
Now put 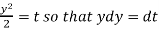

Integrate by parts-
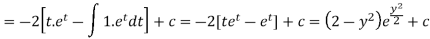
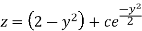
Or
Example: Solve 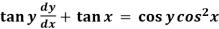
Sol. Here given,
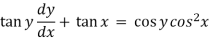
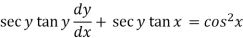
Now let z = sec y, so that dz/dx = sec y tan y dy/dx
Then the equation becomes-
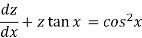
Here,
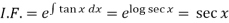
Then the solution will be-
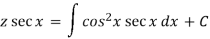
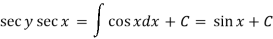
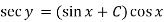
Example: Solve- 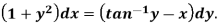
Sol. Here given-
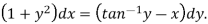
We can re-write this as-
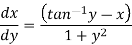

Which is a linear differential equation-
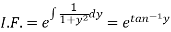
The solution will be-
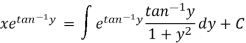
Put 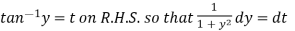
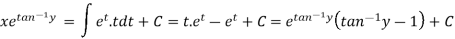
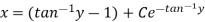
Key takeaways-
- Bernoulli’s equation-

2. A non-linear equation of the form 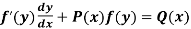 can be reduced to linear equation in z by the substitution z = f(y)
can be reduced to linear equation in z by the substitution z = f(y)
“When every curve of either family cuts each curve of other family at right angle in the two families of curve, then they are orthogonal trajectories of each other.”
Or
Two families of curve such that every member of either family cuts each member of the other family at right angles are called orthogonal trajectories pf each other.
Ex. 1. The line of heat flow is perpendicular to isothermal curve.
Steps to find orthogonal trajectories of curves-:
1. Differentiate the equation of the curve and find the differential equation as below-
f = 0
= 0
2. Replace 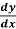 by
by 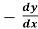
3. Solve the differential equation of the orthogonal trajectories,
f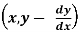 = 0
= 0
Self-orthogonal –
If the family of orthogonal traj. Is same as the family of curves, then it is called self-orthogonal.
Example: If the family of curves is xy = c , then find its orthogonal trajectory.
Sol. First we will differentiate the given equation with respect to x,
We get,
y + x 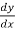 = 0
= 0
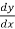 =
= 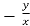
Replace 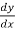 by
by 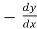
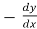 =
= 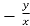
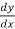 =
= 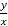
We get,
Ydy = x dx
Now integrate this equation, we get
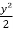 =
= 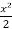 + c
+ c
y² - x² = 2c. Ans.
Example: find the orthogonal trajectory of the family of curves x² - y² = c
Sol. Here we will follow same procedure as we did in above example,
Diff. The given equation w.r.t. x, we get
2x – 2y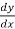 = 0
= 0
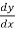 =
= 
Replace 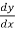 by
by 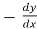
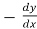 =
= 
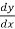 = -
= - 
Ydy = - xdx
Now integrate the above eq.
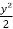 =
= 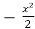 + c
+ c
On solving we get,
x² + y² = 2c.
To find the orthogonal trajectories of the curve 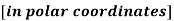
Step-1: Suppose we have the differential equation- P(r,  ,
, 
Then-
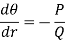
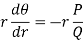
Step-2: the differential equation corresponding to the orthogonal trajectories is-
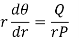
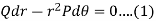
Now solve equation (1), that will be the required orthogonal trajectory.
Example: Find the orthogonal trajectory of 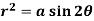 .
.
Sol.
Differentiate the equation with respect to r, we get-

Now eliminate 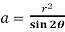 , we get-
, we get-
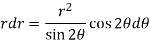
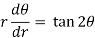
Differential equation of orthogonal trajectory-
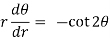
On solving-
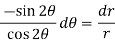

On integrating-
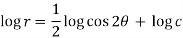
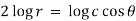
Orthogonal trajectory-
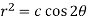
Example: Find the orthogonal trajectory of the cardioids r = a (1 – cos  .
.
Sol.
Here we have-
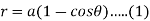
Now differentiate equation (1) with respect to 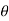
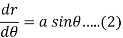
Divide 2 by 1 to eliminate ‘a’, we get-
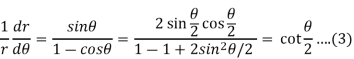
This is the differential equation of (1).
Replace 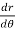 by
by  in (3),
in (3),
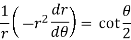
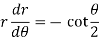
Or
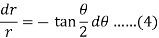
Now integrate (4),
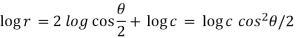
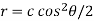
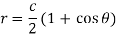
Which is the required answer.
Key takeaways-
- If each curve in either family is orthogonal to every curve in the other family. In this case the two families are said to be mutually orthogonal and each family is said to be the orthogonal trajectories of the other family.
- Two curves cut at right angles if the angle between their corresponding tangents at the point of intersection is 90degree.
- Some examples of orthogonal trajectories are- Meridians and parallels on world globe, Lines of heat flow and isothermal curves, Curves of steepest descent and contour lines on a map
- If the family of orthogonal trajectory Is same as the family of curves, then it is called self-orthogonal.
Applications to Simple Electrical Circuits
A mathematical model of an electric circuit is represented by a linear differential equation.
We need the following results to form such equations-
- The voltage drop
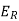 across a resistor is proportional to the current I(t) through it.
across a resistor is proportional to the current I(t) through it.
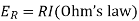
Here t is the time proportionality constant R is resistance.
2. The voltage drop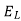 across an inductor is proportional to the time rate change of the current-
across an inductor is proportional to the time rate change of the current-
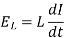
Here L is known as inductance of the indicator.
We measure L in henrys (H).
3. The voltage drop 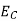 across a capacitor is proportional to the electric charge Q on the capacitor.
across a capacitor is proportional to the electric charge Q on the capacitor.

Here C is called the capacitance and it is measured in Faradays (F)
Kirchhoff’s voltage law-
The algebraic sum of all the instantaneous voltage drops around any closed loop is zero or the voltage impressed on a closed loop is equal to the sum of the voltage drops in the rest of the loop.
RL Circuit-
According to the Kirchhoff’s law to the RL circuit-
The sum of the two voltage drops must be equal to electromotive force E(t ). Thus the current I (t ) in the RL-circuit is determined by the first order linear differential equation.
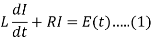
Or
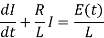
Which has an I.F.
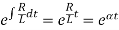
Where 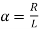
The general solution of (1) is-
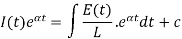
Or
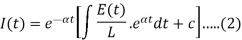
Case- If E = 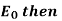 equation (2) becomes-
equation (2) becomes-
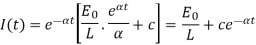
Case-2: If E = 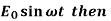 equation (2) becomes-
equation (2) becomes-
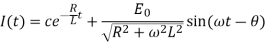
Case-3: If E = 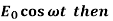 equation (2) becomes-
equation (2) becomes-
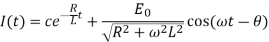
Here
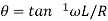
RC- circuit-
By using 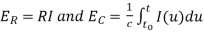
We get-

Which becomes on differentiating-
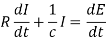
Or
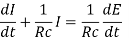
It has I.F.
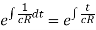
The general solution is-
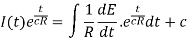
Or
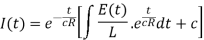
Example: A capacitor c = 0.01 F in series with a resistor R = 20 ohms is charged from a battery E0 = 10 V. Assuming that initially the capacitor is completely uncharged, determine the charge Q(t ), voltage v(t ) on the capacitor and the current I (t ) in the circuit.
Sol.
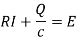
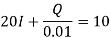
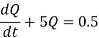
The general solution is-
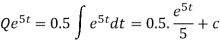
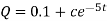
At t = 0, Q = 0
So that-

Thus, Q(t) = 0.1 (1 – 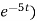
Voltage,
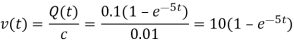
The current I(t) = dQ/dt = 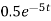
Key takeaways-
- Kirchhoff’s voltage law- The algebraic sum of all the instantaneous voltage drops around any closed loop is zero or the voltage impressed on a closed loop is equal to the sum of the voltage drops in the rest of the loop
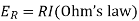

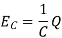
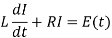
Newton’s law of cooling-
Definition- The temperature of a body changes at a rate which is proportional to the difference in temperature between that of the surrounding medium and that of the body itself.
If 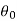 is the temperature of the surroundings and
is the temperature of the surroundings and 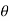 that of the body at any time t, then-
that of the body at any time t, then-
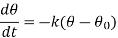
Here k is a constant.
Example: A body originally at 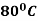 cools down to
cools down to 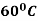 in 20 minutes. The temperature of the air being
in 20 minutes. The temperature of the air being 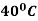 . What will be the temperature of the body after 40 minutes from the original?
. What will be the temperature of the body after 40 minutes from the original?
Sol.
If  is the temperature of the surroundings and
is the temperature of the surroundings and 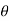 that of the body at any time t, then-
that of the body at any time t, then-
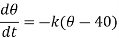
On integrating-
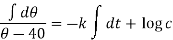
Or
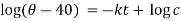
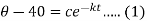
When t = 0 and 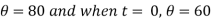
So that-
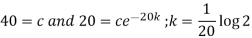
Then equation-1 becomes-
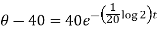
When t = 40 min, then-
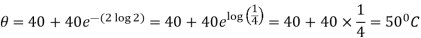
Example: If a substance cools from 370 k to330 k in 10 mts, when the temperature of the surrounding air is 290 k, find the temperature of the substance after 40 mts.
Sol.
Here we have,

So that the solution is-
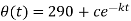
Using condition T(0) = 370 to find c.

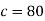
Thus-
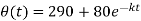
Now use condition,
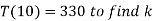
Thus
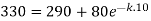
So that-
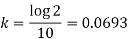
So that the required solution is-
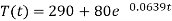
Putting t = 40mts in the equation-

Key takeaways-
If 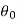 is the temperature of the surroundings and
is the temperature of the surroundings and 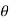 that of the body at any time t, then-
that of the body at any time t, then-
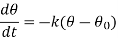
Here k is a constant.
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.
Unit - 1
ODE of First order and Degree and Application
Differential Equations (Definition) –
A differential equation is an equation involving an unknown function and
Its derivatives.
Ex. 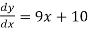
“A differential equation is an ordinary differential equationif the unknown function depends on only one independent variable.”
Notation:
The expression y’, y’’ , y’’’ …….yⁿ are used to represent derivatives.
Here, y’ = 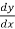 , y’’ =
, y’’ = 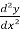 and so on.
and so on.
1st order linear differential equations-
A 1st order linear differential equations is linear when it is given in the form below-
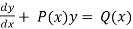 ,
,
Where P(x) and Q(x) are the functions of x
Here we will learn about degree and order of an ordinary differential equation.
Order:
The order is the highest derivative:
For example:
(1) 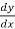 + y³ = 8x , here it has only first derivative so its ‘first order’.
+ y³ = 8x , here it has only first derivative so its ‘first order’.
(2)  + y³ = 7x , here it has a second derivative so its ‘second order’ and so on.
+ y³ = 7x , here it has a second derivative so its ‘second order’ and so on.
Degree:
Degree is known as the exponent of higher derivative.
For example:
1.  )² + y³ = 8x, here its highest derivative has an exponent of 2, it is a first order second degree ordinary differential equation.
)² + y³ = 8x, here its highest derivative has an exponent of 2, it is a first order second degree ordinary differential equation.
2. 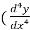 ) +
) + 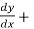 y³ = 8x, here in this example its higher derivative has no exponent, so we can say that this is the third order and first degree ordinary differential equation.
y³ = 8x, here in this example its higher derivative has no exponent, so we can say that this is the third order and first degree ordinary differential equation.
Note-
- A solution to a differential equation which contains one or more arbitrary constants of integration is called general solution.
- If additional information is given so that constant may be calculated the particular solution additional information are boundary conditions.
Formation of differential equations
We can form a differential equation by differentiating the ordinary equation and eliminating the arbitrary constant.
Example: From the differential equation by eliminating arbitrary constant.
y = A cos x + B sin x
Sol. Differentiate the given equation,
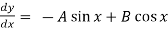 -----------------(1)
-----------------(1)
Now, we will differentiate equation (1) again,

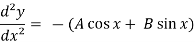
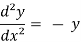
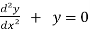 ans.
ans.
Example: From the differential equation by eliminating arbitrary constant.
y² = Ax² + Bx² + C
Sol.
We will differentiate the given function, we get
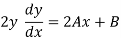
Again differentiate,
 + 2
+ 2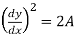
On differentiating again, we get
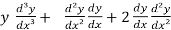 = 0
= 0
Example: Obtain the differential equation of 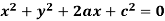 here c is a constant and ‘a’ is a variable.
here c is a constant and ‘a’ is a variable.
Sol.
Here we have,
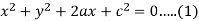
Differentiate with respect to ‘x’, we get-
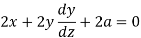
Or
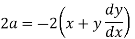
Put this value in (1),
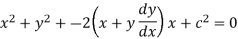
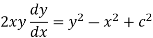
Which is the required DE.
General and particular solutions
A relation between the variables which satisfies the given DE, is called the solution of that DE.
General solution-
The general solution of a DE is that in which the number of arbitrary constants is equals to the order of DE. General solution is also called complete solution.
Particular solution-
A particular solution is that which can be obtained from the general solution by giving particular values to the arbitrary constants.
Let’s understand how to solve differential equations:
(1) The solution of equations of the form 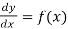
This type of equation can be solved by direction integration:
Y = 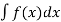
Example: Find the general solution of x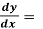 2 – 4x³
2 – 4x³
Solution: rearranging the given equation:
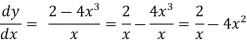
On integrating both sides,
y = 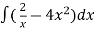 = 2 In x -
= 2 In x - 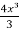 + c
+ c
This is the general solution.
Example: Find the particular solution of the differential equation 5 , given the boundary condition y = 1
, given the boundary condition y = 1 , when x = 2.
, when x = 2.
Solution:
Rearrange the diff. Equation,
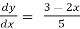 =
=  -
- 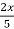
y = 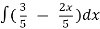 =
= 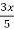 -
- 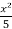 + c, which is the general solution.
+ c, which is the general solution.
Put the boundary conditions to find c,
1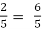 -
- 
Which gives, c = 1
Hence the particular solution is,
y =  -
- 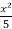 + 1.
+ 1.
(2) The solution of equation of the form 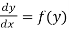 ,
,
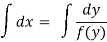
Example: Find the general solution of 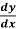 = 3 + 2y
= 3 + 2y
Solution: here, 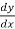 = 3 + 2y gives,
= 3 + 2y gives,
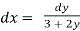 ,
,
Integrating both sides,
 ,
,
By substitution, u = (3 +2y),
X =  In(3 + 2y) + c.
In(3 + 2y) + c.
Example: Determine the particular solution of (y² - 1)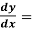 3y given that y =1 when x = 2
3y given that y =1 when x = 2 .
.
Solution: It gives,
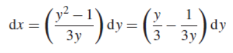
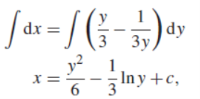
When putting the values, y =1 ,x = 2 ,
,
The particular solution will be,
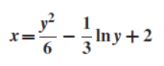
(3) The solution of equation of the form 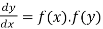
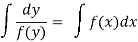
Example-1: Solve the equation 4xy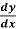 = y² - 1
= y² - 1
Solution: on separating variables, we get
(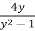 ) dy =
) dy = dx
dx
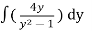 =
= 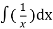
Using substitution, u = y² - 1
2In(y² - 1) = In x + c.
Example-2: Determine the particular solution of 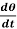 = 2
= 2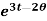 , given that t = 0, when θ = 0
, given that t = 0, when θ = 0
Solution: 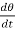 = 2
= 2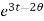 = 2
= 2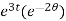 ,
,
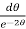 = 2
= 2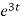 dt
dt
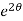 dθ =
dθ =  dt
dt
Now integrating both sides,
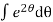 =
= 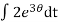
The general solution is ,
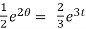 + c.
+ c.
When t = 0 and θ = 0, c =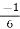
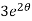 =
= 
Key takeaways:
- “A differential equation is an ordinary differential equationif the unknown function depends on only one independent variable.”
- The order is the highest derivative:
- Degree is known as the exponent of higher derivative.
- A solution to a differential equation which contains one or more arbitrary constants of integration is called general solution.
- A relation between the variables which satisfies the given DE, is called the solution of that DE.
Exact differential equations
Definition-
An exact differential equation is formed by differentiating its solution directly without any other process,
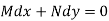
Is called an exact differential equation if it satisfies the following condition-
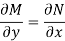
Here 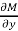 is the differential co-efficient of M with respect to y keeping x constant and
is the differential co-efficient of M with respect to y keeping x constant and 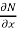 is the differential co-efficient of N with respect to x keeping y constant.
is the differential co-efficient of N with respect to x keeping y constant.
Step by step method to solve an exact differential equation-
1. Integrate M w.r.t. x keeping y constant.
2. Integrate with respect to y, those terms of N which do not contain x.
3. Add the above two results as below-
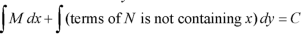
Provided 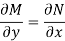
Example-1: Solve 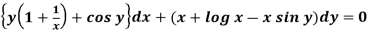
Sol.
Here M = 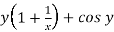 and N =
and N = 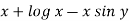
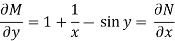
Then the equation is exact and its solution is-
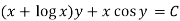
Example-2: Solve-
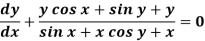
Sol. We can write the equation as below-
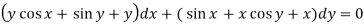
Here M = 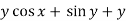 and N =
and N = 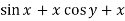
So that-
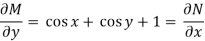
The equation is exact and its solution will be-

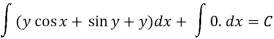
Or
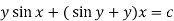
Example-3: Determine whether the differential function ydx –xdy = 0 is exact or not.
Solution. Here the equation is the form of M(x , y)dx + N(x , y)dy = 0
But, we will check for exactness,
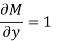
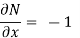
These are not equal results, so we can say that the given diff. Eq. Is not exact.
Example: Solve-
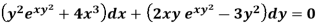
Sol.
Here, M = 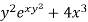 and N =
and N = 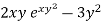
So that-
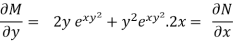
Thus the equation is exact and its solution is-

Which means-

Or
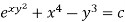
Key takeaways-
- The necessary condition for exactness-

2. 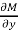 is the differential co-efficient of M with respect to y keeping x constant
is the differential co-efficient of M with respect to y keeping x constant
3. 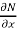 is the differential co-efficient of N with respect to x keeping y constant
is the differential co-efficient of N with respect to x keeping y constant
Reducible to Exact differential equations
Equation reducible to exact form-
1. If M dx + N dy = 0 be an homogenous equation in x and y, then 1/ (Mx + Ny) is an integrating factor (M dx + N dy 
Example: Solve-
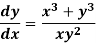
Sol.
We can write the given equation as-
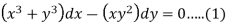
Here,
M = 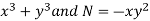
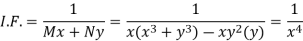
Multiply equation (1) by 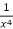 we get-
we get-

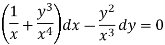
This is an exact differential equation-
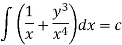
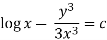
Example: Solve-
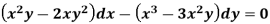
Sol.
The equation given is homogeneous in x and y-
Now, the integrating factor is-
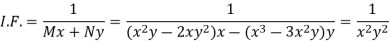
Multiply by 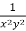 , the equation reduces to-
, the equation reduces to-
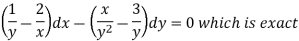
Now the solution is-
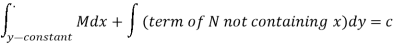
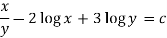
2. I.F. For an equation of the type 
IF the equation Mdx + Ndy = 0 be this form, then 1/(Mx – Ny) is an integrating factor.
Example: Solve-
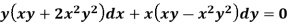
Sol.
Here we have-

Now divide by xy, we get-
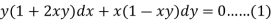

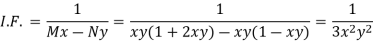
Multiply (1) by 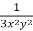 , we get-
, we get-
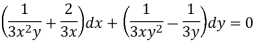
Which is an exact differential equation-
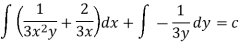
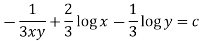

3. In the equation M dx + N dy = 0,
(i) If 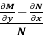 be a function of x only = f(x), then
be a function of x only = f(x), then 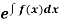 is an integrating factor.
is an integrating factor.
(ii) If 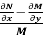 be a function of y only = F(x), then
be a function of y only = F(x), then 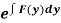 is an integrating factor.
is an integrating factor.
Example: Solve-

Sol.
Here given,
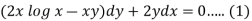
M = 2y and N = 2x log x - xy
Then-
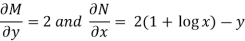
Here,
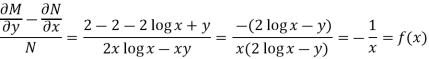
Then,
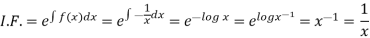
Now multiplying equation (1) by 1/x, we get-
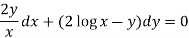
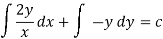
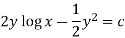
4. For the following type of equation-

An I.F. Is 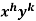
Where-
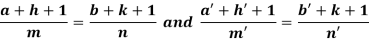
Example: Solve-
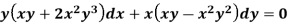
Sol.
We can write the equation as below-
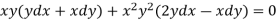
Now comparing with-
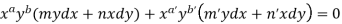
We get-
a = b = 1, m = n = 1, a’ = b’ = 2, m’ = 2, n’ = -1
I.F. = 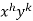
Where-
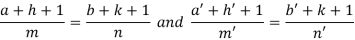

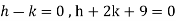
On solving we get-
h = k = -3
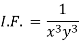
Multiply the equation by  , we get-
, we get-
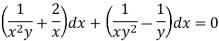
It is an exact equation.
So that the solution is-
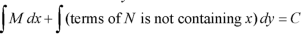
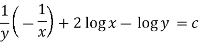
Linear differential equations
A differential equation of the form
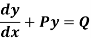
Is called linear differential equation.
This is the standard form of a linear differential equation.
It is also called Leibnitz’s linear equation.
Here P and Q are the function of x
Note-
A differential equation is said to be linear if the dependent variable and differentia coefficient occur only in the first degree and not multiplied together.
Working rule
(1) Convert the equation to the standard form 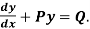
(2) Find the integrating factor.
(3) Then the solution will be y(I.F) = 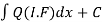
Where integrating factor (I.F.) is = 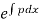
Example-1: Solve-
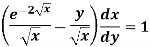
Sol. We can write the given equation as-
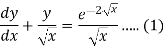
So that-
I.F. = 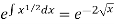
The solution of equation (1) will be-
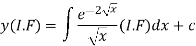
Or
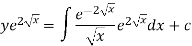
Or
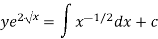
Or
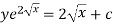
Example-2: Solve-
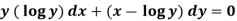
Sol.
We can write the equation as-
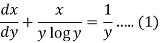
We see that it is a Leibnitz’s equation in x-
So that-

Therefore the solution of equation (1) will be-
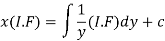
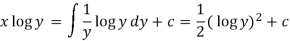
Or
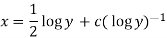
Example-3: Solve sin x 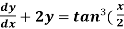 )
)
Solution: here we have,
Sin x  )
)
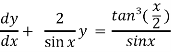
Which is the linear form,
Now,
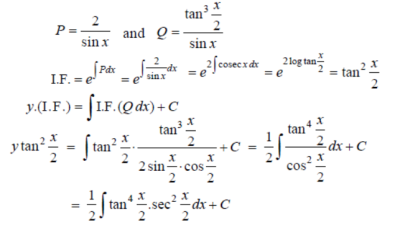
Put tan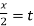 so that
so that  sec²
sec²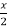 dx = dt, we get
dx = dt, we get
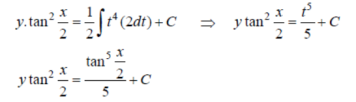
Which is the required solution.
Key takeaways-
- The form a linear differential equation-
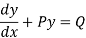
2. A differential equation is said to be linear if the dependent variable and differentia coefficient occur only in the first degree and not multiplied together
3. I.F. = 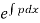
Reducible to Linear differential equations
Bernoulli’s equation-
The equation
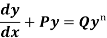
Is reducible to the Leibnitz’s linear equation and is usually called Bernoulli’s equation.
Working procedure to solve the Bernoulli’s linear equation-
Divide both sides of the equation –
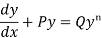
By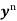 , so that
, so that

Put 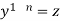 so that
so that 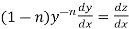
Then equation (1) becomes-
 )
)
Here we see that it is a Leibnitz’s linear equations which can be solved easily.
Example: Solve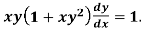
Sol.
We can write the equation as-

On dividing by 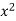 , we get-
, we get-
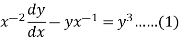
Put 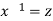 so that
so that 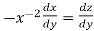
Equation (1) becomes,
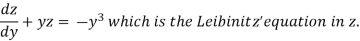
Here,
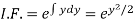
Therefore the solution is-
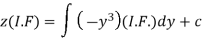
Or
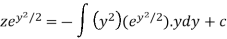
Now put 

Integrate by parts-
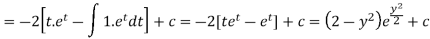
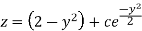
Or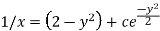
Example: Solve 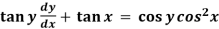
Sol. Here given,
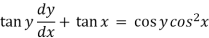
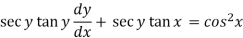
Now let z = sec y, so that dz/dx = sec y tan y dy/dx
Then the equation becomes-
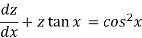
Here,
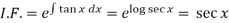
Then the solution will be-
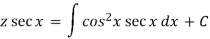
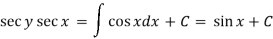
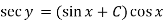
Example: Solve- 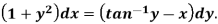
Sol. Here given-
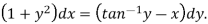
We can re-write this as-
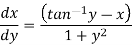
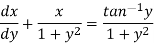
Which is a linear differential equation-
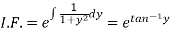
The solution will be-
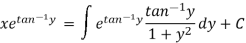
Put 
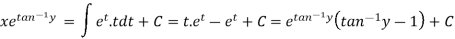
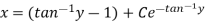
Key takeaways-
- Bernoulli’s equation-

2. A non-linear equation of the form 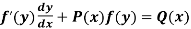 can be reduced to linear equation in z by the substitution z = f(y)
can be reduced to linear equation in z by the substitution z = f(y)
“When every curve of either family cuts each curve of other family at right angle in the two families of curve, then they are orthogonal trajectories of each other.”
Or
Two families of curve such that every member of either family cuts each member of the other family at right angles are called orthogonal trajectories pf each other.
Ex. 1. The line of heat flow is perpendicular to isothermal curve.
Steps to find orthogonal trajectories of curves-:
1. Differentiate the equation of the curve and find the differential equation as below-
f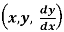 = 0
= 0
2. Replace 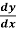 by
by 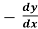
3. Solve the differential equation of the orthogonal trajectories,
f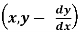 = 0
= 0
Self-orthogonal –
If the family of orthogonal traj. Is same as the family of curves, then it is called self-orthogonal.
Example: If the family of curves is xy = c , then find its orthogonal trajectory.
Sol. First we will differentiate the given equation with respect to x,
We get,
y + x 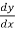 = 0
= 0
 =
= 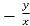
Replace 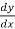 by
by 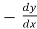
 =
= 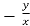
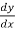 =
= 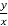
We get,
Ydy = x dx
Now integrate this equation, we get
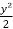 =
= 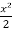 + c
+ c
y² - x² = 2c. Ans.
Example: find the orthogonal trajectory of the family of curves x² - y² = c
Sol. Here we will follow same procedure as we did in above example,
Diff. The given equation w.r.t. x, we get
2x – 2y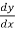 = 0
= 0
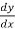 =
= 
Replace 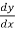 by
by 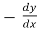
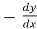 =
= 
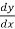 = -
= - 
Ydy = - xdx
Now integrate the above eq.
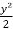 =
= 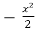 + c
+ c
On solving we get,
x² + y² = 2c.
To find the orthogonal trajectories of the curve 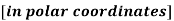
Step-1: Suppose we have the differential equation- P(r, 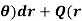 ,
, 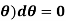
Then-

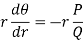
Step-2: the differential equation corresponding to the orthogonal trajectories is-
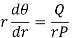
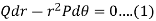
Now solve equation (1), that will be the required orthogonal trajectory.
Example: Find the orthogonal trajectory of 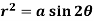 .
.
Sol.
Differentiate the equation with respect to r, we get-
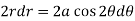
Now eliminate 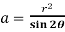 , we get-
, we get-
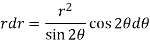
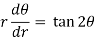
Differential equation of orthogonal trajectory-

On solving-
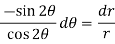

On integrating-
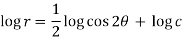
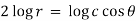
Orthogonal trajectory-

Example: Find the orthogonal trajectory of the cardioids r = a (1 – cos 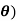 .
.
Sol.
Here we have-

Now differentiate equation (1) with respect to 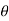
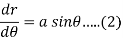
Divide 2 by 1 to eliminate ‘a’, we get-
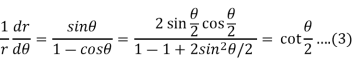
This is the differential equation of (1).
Replace 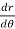 by
by 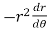 in (3),
in (3),
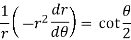

Or
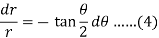
Now integrate (4),
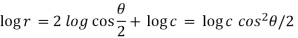
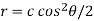
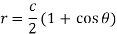
Which is the required answer.
Key takeaways-
- If each curve in either family is orthogonal to every curve in the other family. In this case the two families are said to be mutually orthogonal and each family is said to be the orthogonal trajectories of the other family.
- Two curves cut at right angles if the angle between their corresponding tangents at the point of intersection is 90degree.
- Some examples of orthogonal trajectories are- Meridians and parallels on world globe, Lines of heat flow and isothermal curves, Curves of steepest descent and contour lines on a map
- If the family of orthogonal trajectory Is same as the family of curves, then it is called self-orthogonal.
Applications to Simple Electrical Circuits
A mathematical model of an electric circuit is represented by a linear differential equation.
We need the following results to form such equations-
- The voltage drop
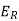 across a resistor is proportional to the current I(t) through it.
across a resistor is proportional to the current I(t) through it.
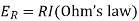
Here t is the time proportionality constant R is resistance.
2. The voltage drop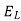 across an inductor is proportional to the time rate change of the current-
across an inductor is proportional to the time rate change of the current-
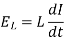
Here L is known as inductance of the indicator.
We measure L in henrys (H).
3. The voltage drop 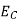 across a capacitor is proportional to the electric charge Q on the capacitor.
across a capacitor is proportional to the electric charge Q on the capacitor.
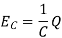
Here C is called the capacitance and it is measured in Faradays (F)
Kirchhoff’s voltage law-
The algebraic sum of all the instantaneous voltage drops around any closed loop is zero or the voltage impressed on a closed loop is equal to the sum of the voltage drops in the rest of the loop.
RL Circuit-
According to the Kirchhoff’s law to the RL circuit-
The sum of the two voltage drops must be equal to electromotive force E(t ). Thus the current I (t ) in the RL-circuit is determined by the first order linear differential equation.
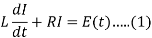
Or
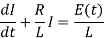
Which has an I.F.
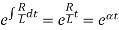
Where 
The general solution of (1) is-

Or
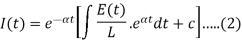
Case- If E =  equation (2) becomes-
equation (2) becomes-
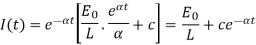
Case-2: If E = 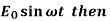 equation (2) becomes-
equation (2) becomes-
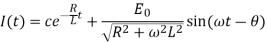
Case-3: If E = 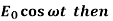 equation (2) becomes-
equation (2) becomes-
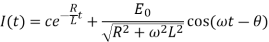
Here
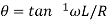
RC- circuit-
By using 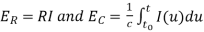
We get-

Which becomes on differentiating-
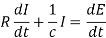
Or
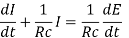
It has I.F.
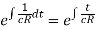
The general solution is-
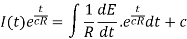
Or
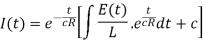
Example: A capacitor c = 0.01 F in series with a resistor R = 20 ohms is charged from a battery E0 = 10 V. Assuming that initially the capacitor is completely uncharged, determine the charge Q(t ), voltage v(t ) on the capacitor and the current I (t ) in the circuit.
Sol.
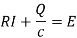
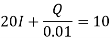

The general solution is-
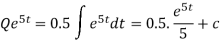
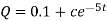
At t = 0, Q = 0
So that-
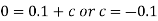
Thus, Q(t) = 0.1 (1 – 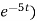
Voltage,
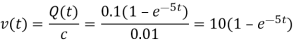
The current I(t) = dQ/dt = 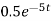
Key takeaways-
- Kirchhoff’s voltage law- The algebraic sum of all the instantaneous voltage drops around any closed loop is zero or the voltage impressed on a closed loop is equal to the sum of the voltage drops in the rest of the loop
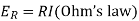
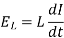
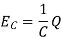

Newton’s law of cooling-
Definition- The temperature of a body changes at a rate which is proportional to the difference in temperature between that of the surrounding medium and that of the body itself.
If 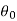 is the temperature of the surroundings and
is the temperature of the surroundings and  that of the body at any time t, then-
that of the body at any time t, then-
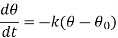
Here k is a constant.
Example: A body originally at 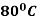 cools down to
cools down to 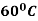 in 20 minutes. The temperature of the air being
in 20 minutes. The temperature of the air being 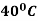 . What will be the temperature of the body after 40 minutes from the original?
. What will be the temperature of the body after 40 minutes from the original?
Sol.
If 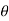 is the temperature of the surroundings and
is the temperature of the surroundings and 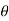 that of the body at any time t, then-
that of the body at any time t, then-
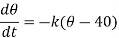
On integrating-
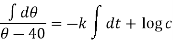
Or
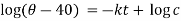
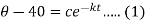
When t = 0 and 
So that-
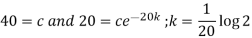
Then equation-1 becomes-
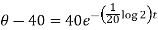
When t = 40 min, then-
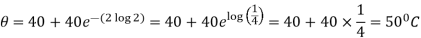
Example: If a substance cools from 370 k to330 k in 10 mts, when the temperature of the surrounding air is 290 k, find the temperature of the substance after 40 mts.
Sol.
Here we have,

So that the solution is-
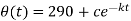
Using condition T(0) = 370 to find c.
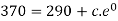
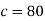
Thus-
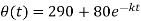
Now use condition,
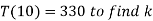
Thus
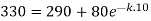
So that-
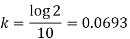
So that the required solution is-
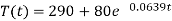
Putting t = 40mts in the equation-
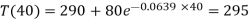
Key takeaways-
If 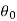 is the temperature of the surroundings and
is the temperature of the surroundings and 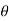 that of the body at any time t, then-
that of the body at any time t, then-
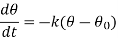
Here k is a constant.
References:
- E. Kreyszig, “Advanced Engineering Mathematics”, John Wiley & Sons, 2006.
- P. G. Hoel, S. C. Port And C. J. Stone, “Introduction To Probability Theory”, Universal Book Stall, 2003.
- S. Ross, “A First Course in Probability”, Pearson Education India, 2002.
- W. Feller, “An Introduction To Probability Theory and Its Applications”, Vol. 1, Wiley, 1968.
- N.P. Bali and M. Goyal, “A Text Book of Engineering Mathematics”, Laxmi Publications, 2010.
- B.S. Grewal, “Higher Engineering Mathematics”, Khanna Publishers, 2000.